ГОСТ 11.009-79
Система управления качеством продукции. Прикладная статистика. Правила определения оценок и доверительных границ для параметров логарифмически нормального распределения
Купить ГОСТ 11.009-79 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Устанавливает правила определения оценок и доверительных границ для параметров логарифмически нормального распределения по совокупности статистических данных, если эти данные подчинены логарифмически нормальному распределению. Проверка согласия опытного распределения этих данных с логарифмически нормальным производится по ГОСТ 11.006-75.
Отменен без замены.
Оглавление
1. Общие положения
2. Оценки параметров a и сигма
3. Определение доверительных границ для параметра a
4. Определение доверительных границ для параметра сигма
5. Случай цензурированной выборки
6. Случай усеченной выборки
Приложение 1 (справочное) Примеры применения правил стандарта
Приложение 2 (рекомендуемое) Способ нахождения оценки параметра сигма через размах
Приложение 3 (справочное) Оценки для математического ожидания и дисперсии логарифмически нормального распределения; доверительные границы для математического ожидания
Приложение 4 (рекомендуемое) Использование натуральных логарифмов
Приложение 5 (справочное) Теоретические основы стандарта
Литература
| Дата введения | 01.07.1980 |
|---|---|
| Добавлен в базу | 01.01.2019 |
| Завершение срока действия | 01.03.1987 |
| Актуализация | 01.01.2021 |
Организации:
| 28.09.1979 | Утвержден | Государственный комитет СССР по стандартам | 3768 |
|---|---|---|---|
| Разработан | ВНИИС | ||
| Издан | Издательство стандартов | 1980 г. |
Product quality control system. Applied statistics. Point and interval estimators for parameters of logarithmico-normal distribution
- ГОСТ 11.003-73 Прикладная статистика. Равномерно распределенные случайные числа
- ГОСТ 11.004-74 Прикладная статистика. Правила определения оценок и доверительных границ для параметров нормального распределения
- ГОСТ 11.008-75 Прикладная статистика. Графические методы обработки данных. Метод вероятностных сеток
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7
стр. 8
стр. 9
стр. 10

стр. 11
стр. 12
стр. 13
стр. 14

стр. 15

стр. 16
стр. 17

стр. 18

стр. 19
стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26

стр. 27
стр. 28

стр. 29

стр. 30
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
СИСТЕМА УПРАВЛЕНИЯ КАЧЕСТВОМ ПРОДУКЦИИ. ПРИКЛАДНАЯ СТАТИСТИКА
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ Москва
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
СИСТЕМА УПРАВЛЕНИЯ КАЧЕСТВОМ ПРОДУКЦИИ. ПРИКЛАДНАЯ СТАТИСТИКА
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Издание официальное
МОСКВА —1980
|
Продолжение табл. 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Примечание. Для отсутствующих в табл. 4 и 5 значений К величины Zu, zt находят линейной интерполяцией по К. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
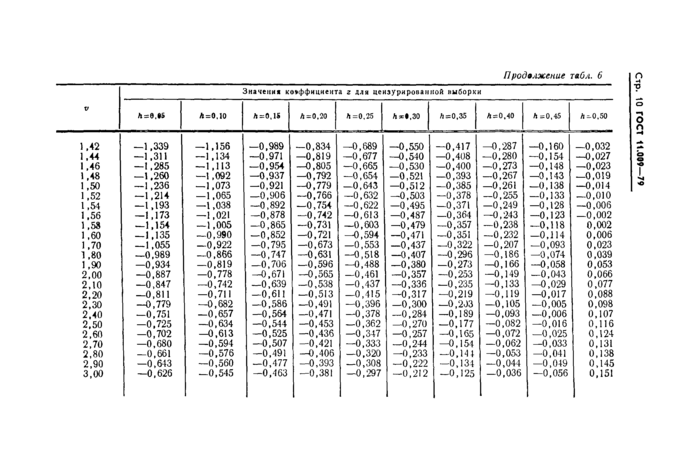
5. СЛУЧАЙ ЦЕНЗУРИРОВАННОЙ ВЫБОРКИ*
5.1. В этом разделе используются следующие обозначения: п— объем всей выборки;
m — число известных элементов;
h — n~m . (17)
п
5.2. Выборка, цензурированная слева (т. е. Xi^d для известных элементов хь__. . ., хгп).
5.2.1. Оценки а и s параметров а и а соответственно находят следующим образом: вычисляют
У (lg Xi—lg d)J
v=m-!—^-; (18)
m
Og-*»—lg d)Y
находят z по табл. 6, в которую входят со значениями h и у, найденными соответственно по формулам (17) и (18); находят f\(z) в табл. 7 по найденному значению г; вычисляют s по формуле
У 0g Xi—lg d)
(19)
S =_L=*__izi_
hfi (•?)—(!—.h) z m
Определение цензурированной выборки дано в справочном приложении 5.
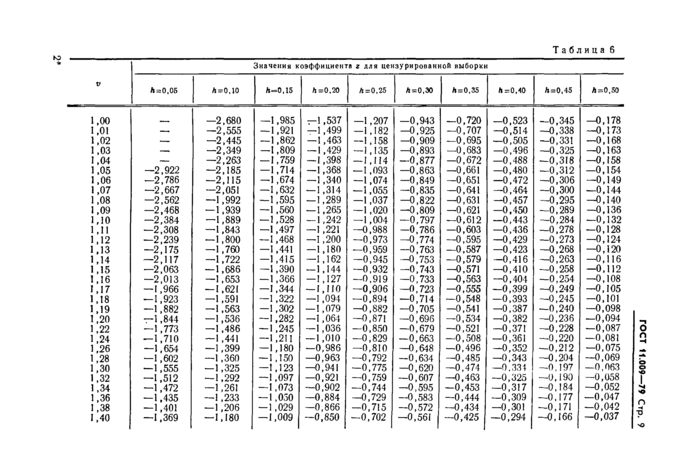
|
Таблица б | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ГОСТ 11.009-79 Стр. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Продолжение табл. 6 | |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
Стр. 10 ГОСТ 11.009-79
ГОСТ 11.009-79 Стр. 11
вычисляют а по формуле
a—lg d—zs, (20)
где г и s определяют как указано выше.
5.2.2. Доверительные границы для параметров а и а находят
по формулам
|
ан—а «Т ,_У72(2); У п |
(21) |
|
aB—a+Uf ■ —У /2(г); У п |
(22) |
|
°„=s ит лг—V Л(г); V П |
(23) |
|
oB_s+«T тV Мг), V П |
(24) |
|
где щ находят по табл. 3: z, s,~a находят как в п. 5.2.1; f2(z), Ыг) находят в табл. 7 по найденному значению г. Таблица 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Продолжение табл. 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Эти формулы обеспечивают точность, достаточную для практических целей, при объеме выборки 20.
5.3. Выборка, цензурированная справа (т. е. xt^Ldf для известных пг элементов выборки хи • ■ 1, хт).
Результаты обрабатываются так же, как указано в пп. 5.2.1; 5.2.2 со следующими изменениями.
Формулу (19) для вычисления s заменяют на
т
У(1 gd'~\gXi)
S = -Ь1---
A/i (г)-(1 -А)1_ т Формулу (20) для вычисления а заменяют на
a—zs-{- lg d\ (26)
Прочие формулы пп. 5,2.1 и 5.2.2 остаются без изменений (см. примеры 7 и 8 справочного приложения 1).
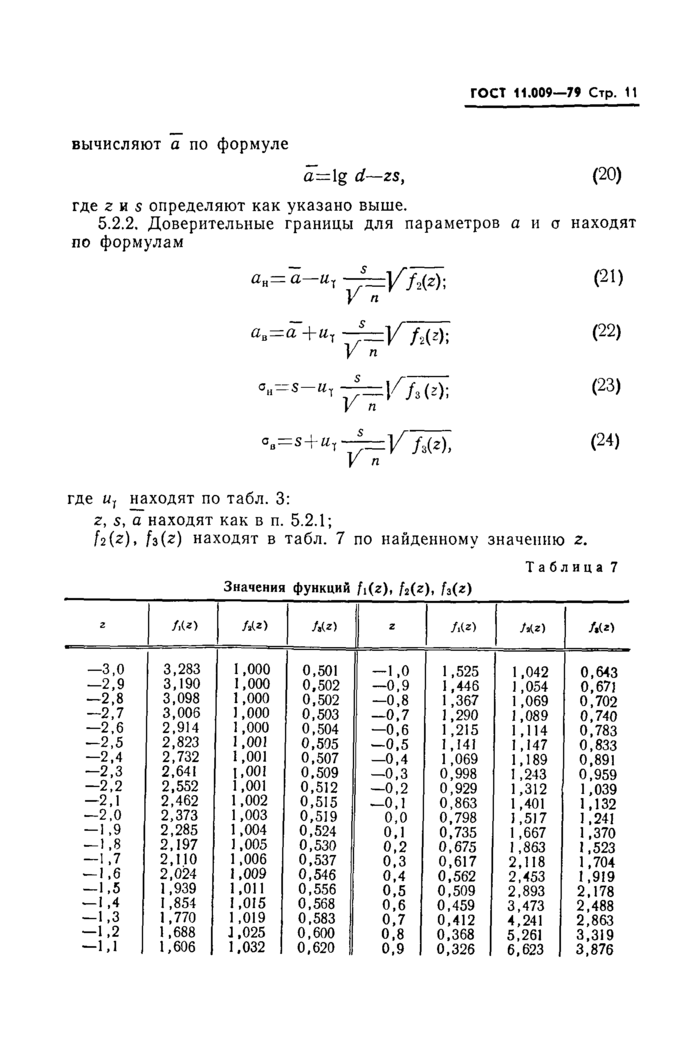
6. СЛУЧАЯ УСЕЧЕННОЙ ВЫБОРКИ1
6.1. Оценки параметров а и а находят следующим образом: вычисляют v по формуле (18), где т — число известных элементов выборки;
находят г по табл. 8, в которую входят со значением t>, найденным по формуле (18);
находят gi(z) из табл. 9 по найденному значению г; вычисляют s по формуле
т
2dg •g d)
gi(2) ■ для выборки, усеченной слева;
5 —
т
т
d-—\g xt)
gif2) —-для выборки, усеченной справа;
т
ГОСТ 11.009-79 Стр. 13
|
вычисляют а по формуле (20) для выборки, усеченной слева, и по формуле (26) для выборки, усеченной справа; в эти формулы подставляют г, найденное по табл. 8, g\ (г), найденное по табл. 9, и | ||||||||||||||
|
где щ находят по табл. 3; г, s, а находят как в п. 6.1;
£2(2), находят в табл. 9 по найденному значению 2.
Эти формулы обеспечивают точность, достаточную для практических целей, при объеме выборки «^20 (см. примеры 9 и 10 справочного приложения 1).
Таблица 8
|
Значения коэффициента z для усеченной выборки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Таблица 9 Значения функций £1(2), g2(z), gi(z) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ГОСТ 11.009-79 Стр. 15
ПРИЛОЖЕНИЕ / Справочное
ПРИМЕРЫ ПРИМЕНЕНИЯ ПРАВИЛ СТАНДАРТА
Пример 1. Имеется выборка объемом 20 из значений случайной величины Х> подчиненнвй логарифмически нормальному распределению. Значения приведены в табл. 1. Найти оценки параметров а и а.
|
Таблица 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение.
Согласно формулам (5), (9), (10) настоящего стандарта находим:
a=3,054,
Sj=0,10602;
S\ =0,326 i s=Mu-sl=l ,013-0,326=0,330.
Пример 2. В условиях предыдущего примера найти односторонние доверительные границы для параметра а при доверительной вероятности у=0»90-Решение. Согласно п. 3.1 для п=20 и у=0,90 по табл. 2 настоящего стандарта находим
V~20 V~20
и по формулам (13) и (14)
ан=3,054—0,330 • 0,297=3,054—0,093=2,956 ; ав=3,054+0,098=3,152.
Пример 3. В условиях примера 1 найти доверительный интервал для параметра а при двусторонней доверительной вероятности у*=0,95.
Решение. По формуле (4) находим
у=0,975.
По табл. 2 настоящего стандарта для п=20 и найденного значения у находим
*0,975 (19> _ 2>086
уГ~20 У20
и по формулам (13) и (14)
ан=3,054—0,330*0,466=3,054—0,154=2,900;
ав=3,054+0,154=3,208.
Пример 4. Дана выборка из 10 значений случайной величины, подчиненной логарифмически нормальному распределению (табл. 2). Известно, что сг = 1,00. Найти доверительный интервал для а при двусторонней доверительной вероятности у* =0,90.
|
Таблица 2 | ||||||||||||||||||||||||||||||||||||
|
Решение. Согласно п. 2.1 настоящего стандарта по формуле (5) находим
а =1,57.
По формуле (13) находим у=0,95 и по табл. 3 настоящего стандарта
и^ =1,645.
По формулам (11) и (12)
а„ = 1,57— ■ 1,(^—1,00=1,57—0,52=1,05;
V 10
ав=1,57+0,52=2,09.
Пример 5. В условиях примера 1 найти верхнюю доверительную границу для параметра а при односторонней доберительной вероятности 7=0,95.
Решение. Согласно разд. 4 настоящего стандарта для /(=19 и 7 = 0,95 из табл. 4 настоящего стандарта находят
гв=1,37.
По формуле (16) ав= 1,37 • 0,330=0,452.
ГОСТ 11.009-79 Стр. 17
Пример 6. В условиях примера 1 найти доверительный интервал для параметра а при двусторонней доверительной вероятности у* =0,90.
Решение. По формуле (4) находим у=0,95.
Из табл. 4 настоящего стандарта находим для /С=19 и у=0,95
-гн=0,794.
По формуле (15) находим
(Г„=0,794-0,330-0,264;
значение <тв = 0,452 найдено в предыдущем примере.
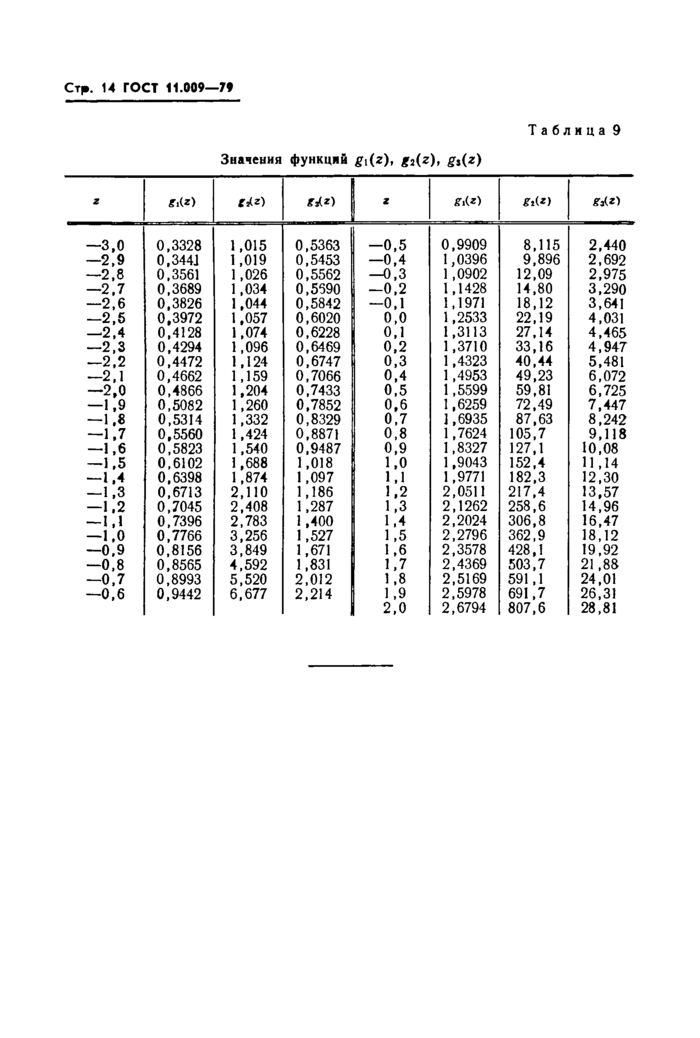
Пример 7. Известно, что наработка некоторого изделия на отказ имеет логарифмически нормальное распределение. Проводились испытания по плану [TV, U, Т] при N — 40, 7=2000 ч (см. ГОСТ 16504-74). Число изделий, отказавших до окончания срока испытания, равно гп=33. В табл 3 приведены результаты испытаний (здесь срок работы i-ro изделия, d' = T = 2000, l'g d' = 3,30l). Найти оценки параметров а и а.
|
Таблица 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение. Здесь, очевидно, имеет место цензурированная справа выборка (см. также п. 5 справочного приложения 5). Согласно п. 5.3 настоящего стандарта находим
33
d'-lg
*i)
12,727,
зз
2<1в d'~[« *()г=6,671
o=33.
6,671
12,7272
=1,359.
РАЗРАБОТАН Всесоюзным научно-исследовательским институтом стандартизации (ВНИИС)
ИСПОЛНИТЕЛИ
▲. М. Бендерский, канд. техн. наук; Н. Б. Левина, канд. физ.-мат. наук; А. А. Богатырев, канд. экон. наук; Н. Г. Миронова; Л. С. Сипатрина; Ю. Д. Филиппов; Л. А. Фомина; 3. Н. Шкотт
ВНЕСЕН Всесоюзным научно-исследовательским институтом стандартизации (ВНИИС)
Директор А. В. Гличев
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 28 сентября 1979 г. № 3768
По табл. 6 настоящего стандарта для 1,359 и с помощью линейной интерполяции находим
40—33 Л= 4сП"
0,175
*=—0,968;
_0,825_
0,175*1,5+0,825.0,968
12,727
33
=0,300;
по формуле (26)
по табл. 7 стандарта находим fi (—0,968) = 1,336; по формуле (25) находим
а =3,301—0,968-0,300=3,011.
Пример 8. В условиях предыдущего примера найти доверительные интервалы для параметров а и а при двусторонней доверительной вероятности у*=0,95.
Решение. По формуле (4) имеет у=0,975 и по табл. 3 настоящего стандарта ал =1,960.
По табл. 7 настоящего стандарта находим
/з(—0,968) = 1,046,
/з(—0,968) =0,652 и по формулам (21) —(24) имеем
Q О _
дн=3,011—1,960- —— - У1,046= 3,011—0,105= 2,906,V 33яв=3,011+0,105=3,116,
яв=3,011+0,105=3,116,
0 3 /
«гн=0,300-1,960- —1--у 0,652=0,300=0,083=0,217,"|/Тзав=0,300+0,083=0,383.
ав=0,300+0,083=0,383.
Пример 9. Известно, что распределение диаметров частиц подчинено логарифмически нормальному распределению. По данным табл. 4 (где Х\ — размеры частиц в мкм) требуется найти параметры этого распределения, если известно, что средство измерения не охватывает всего диапазона изменения диаметров частиц, и часть результатов измерений — именно, когда диаметр частицы не более 100 мкм — не фиксируется.
|
Таблица 4 | ||||||||||||||||||||||||||||||||||||||||||||||||
|
УДК 519.2 : 658.562.014 : 006.354 Группа Т59
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
Система управления качеством продукции. Прикладная статистика
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Product quality control system. Applied statistics. Point and interval estimators for parameters of logarithmico-normal distribution
гост
11.009—79
Постановлением Государственного комитета СССР по стандартам от 28 сентября 1979 г. № 3768 срок введения установлен
с 01.07. 1980 г.
Настоящий стандарт устанавливает правила определения оценок и доверительных границ для параметров логарифмически нормального распределения по совокупности статистических данных, если эти данные подчинены логарифмически нормальному распределению. Проверка согласия опытного распределения этих данных с логарифмически нормальным производится по ГОСТ 11.006-75.
Указанные правила даются как для полностью определенных, так и для неполных однократно усеченных или однократно цензурированных выборок.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Распределение положительной случайной величины X называется логарифмически нормальным, если случайная величина
У= ig х (1)
имеет нормальное распределение (см. ГОСТ 11.004-74).
1.2. Функция распределения величины X имеет вид
F(x) =
|
-QO |
(*-а)а
2 <Ja
, Ug x--a)io __/a/2
dt = -~г Г e dty*tx>% (2)
r J TTf-iTi V*
при
Таким образом, а и а являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины К, определенной по формуле (1).
Издание официальное
Перепечатка воспрещена
©Издательство стандартов, 1980
1.3. Плотность распределения величины X имеет вид
/(*)=■
м
х
е
(lg х—а)2
2о2
0
при jc>0 при х<0,
(3)
где M = \ge=0,4343.
1.4. Для определения оценок и доверительных границ параметров логарифмически нормального распределения можно также пользоваться натуральными логарифмами (см. рекомендуемое приложение 4).
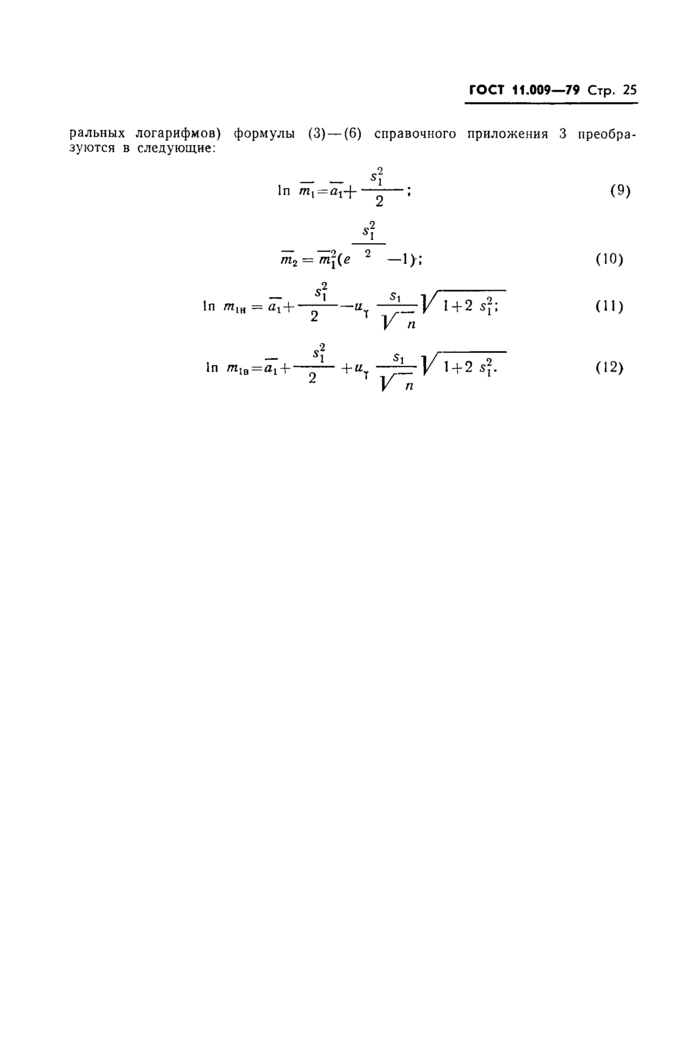
Формулы для математического ожидания и дисперсии величины X, а также оценки для них, даны в справочном приложении 3.
1.5. В разд. 3—6 при определении нижней односторонней доверительной границы пользуются одной из формул (11), (13), (15), (21), (23), (28), (30), где у— заданное значение односторонней доверительной вероятности.
При определении верхней односторонней доверительной границы пользуются одной из формул (12), (14), (16), (22), (24), (29), (31), где у — заданное значение односторонней доверительной вероятности.
При определении доверительного интервала для заданной двусторонней доверительной вероятности у* сначала определяют у по формуле
i±r
2
(4)
Затем пользуются соответствующими формулами, в которых у вычислена по формуле (4).
Доверительный интервал (бесконечный в одностороннем случае и конечный в двустороннем) накрывает значение параметра с вероятностью у в одностороннем случае и у* в двустороннем.
2. ОЦЕНКИ ПАРАМЕТРОВ а и сг
2.1. Оценку а параметра а находят по формуле
а—
(5)
где х\, . . ., х.п — совокупность наблюденных величины X.
2.2. Если значение параметра известно, метра о2 находят по формуле
значений случайной то оценку s2 пара-
п
(6)
ГОСТ 11.009-79 Стр. 3
Если значение параметра а неизвестно, то оценку S2 параметра о2 находят по формуле
S2 =
1
п— 1
^(lg *i—а)\
(7)
i= 1
где а определяют по формуле (5) (см. пример 1 справочного приложения 1).
Оценки (4) — (6) являются несмещенными и состоятельными. 2.3. Оценку S\ параметра а находят по следующим формулам:
5, = ]/ —2(lg х~а? т
i=i
при известном значении а\
*.-«)■ (9)
при неизвестном значении а\ здесь а определяют по формуле (5).
Оценки (8), (9) являются состоятельными, но смещенными. Их можно использовать в тех случаях, когда не требуется большая точность вычислений. В противном случае находят несмещенную оценку для от по формуле
S=MK-SU (10)
где
при известном а находят S\ по формуле (8) и Мк по табл. I при К = п\
при неизвестном а находят Si по формуле (9) и Ля по табл. 1 при К=п—1 (см. пример 1 справочного приложения 1).
|
Таблица 1 Значения коэффициентов М к | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2.4. В случае, когда не требуется большая точность и желательно быстро получить результат, оценки параметров а и а следует определять с помощью вероятностной сетки для логарифмически нормального распределения по ГОСТ 11.008-75. Ориентировочно оценку параметра о можно определять через размах (средний размах) выборки, см. рекомендуемое приложение 2.
3. ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРА а
3.1. Нижнюю и верхнюю доверительные границы (соответственно ан, яв) Для параметра а при известном значении параметра а находят по формулам:
— и- а
ин—а _ > 00
кт
— a.f а
ав=аН—(12)
V п
где а находят по формуле (5), а — по табл. 3 (см. пример 4 справочного приложения 1).
3.2. Доверительные границы для параметра а при неизвестном значении параметра а находят по формулам:
|
UH— CL __, V п — t S |
(13) |
|
ав-а-\—1—, КТ |
(14) |
|
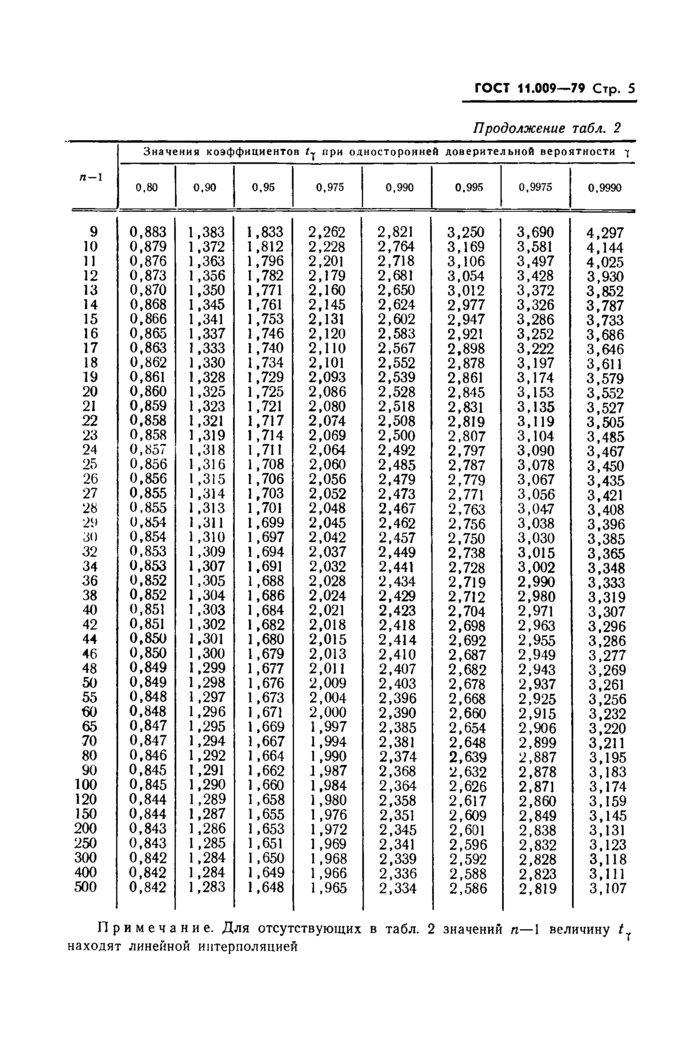
где а и s находят соответственно по формулам (5) и (10), а /т — в табл. 2 по заданным значениям п—1 и у (см. примеры 2 и 3 справочного приложения 1). Таблица 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ГОСТ 11.009—79 Стр. 5
|
Продолжение табл. 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание. Для отсутствующих в табл. 2 значений п—1 величину tт находят линейной интерполяцией
Таблица 3
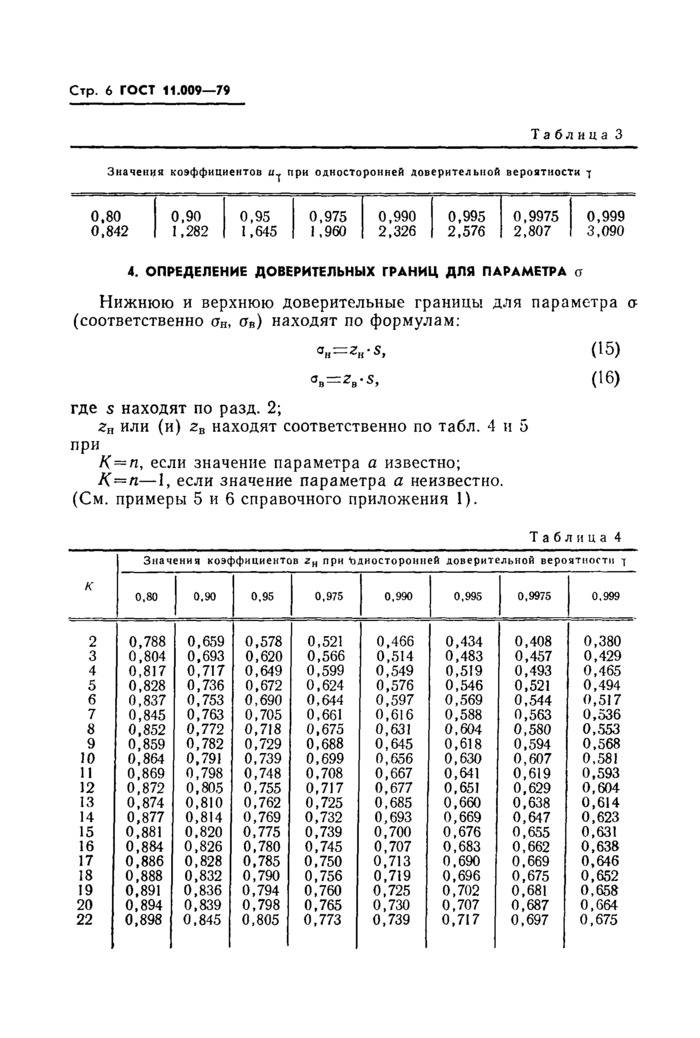
Значения коэффициентов и^ при односторонней доверительной вероятности 7
|
0.80 0,842 |
|
0,999 3,090 | ||||||||||||
|
4. ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРА а | ||||||||||||||
(15)
(16)
Нижнюю и верхнюю доверительные границы для параметра сг-(соответственно ан, <Тв) находят по формулам:
aH^zK*s,
<3В = 2В • 5,
где s находят по разд. 2;
гн или (и) 2В находят соответственно по табл. 4 и 5 при
К = п, если значение параметра а известно;
К=п—1, если значение параметра а неизвестно. (См. примеры 5 и 6 справочного приложения 1).
|
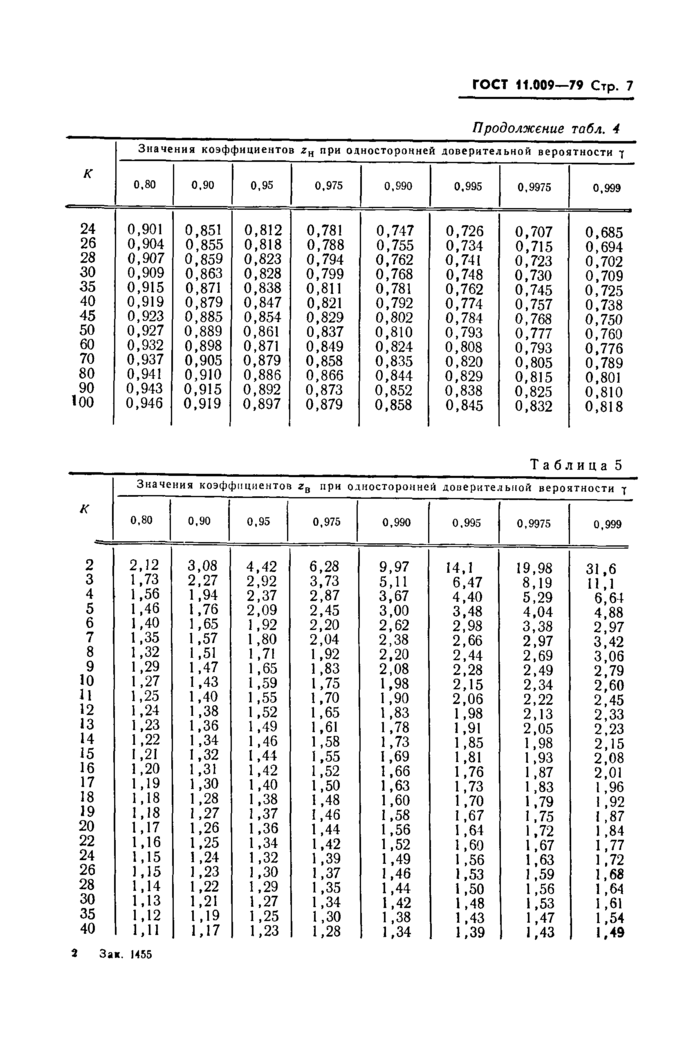
Таблица 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ГОСТ 11.009-79 Стр. 7
|
Продолжение табл. 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
__ Таблица 5 Значения коэффициентов гв при односторонней доверительной вероятности 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 Зак, 1455 |
1
Определение усеченной выборки дано в справочном приложении 5.