ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

ПРИКЛАДНАЯ СТАТИСТИКА

ГРАФИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ ДАННЫХ. МЕТОД ВЕРОЯТНОСТНЫХ СЕТОК

ГОСТ 11.008-75 (СТ СЭВ 3542-82)

Издание официальное

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ Москва

Группа Т59

Applied statisticas. Graphic methods of data processing. (CT СЭ8 3542—82} Use of probability papers

Постановлением Государственного комитета стандартов Совета Министров СССР от 18 сентября 1975 г. № 2434 срок введения установлен

с 01.07,76

Настоящий стандарт устанавливает травила определения оценок статистических характеристик исследуемых объектов с до-мощью графического метода вероятностных сеток при статистической обработке данных, подчиняющихся одному из четырех распределений: нормальному, экспоненциальному, логарифмически ■нормальному и Вейбулла, и 'полученных из полностью определенных выборок.

Настоящий стандарт соответствует СТ СЭВ 3542—82.

(Измененная редакция, Изм. № 1).

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Вероятностная сетка для графического определения оценок характеристик для (конкретного распределения вероятностей представляет собой прямоугольную сетку, на которой масштаб выбран таким образом, чтобы график функции этого распределения, построенный на сетке, представлял собой прямую линию.

Основанием для построения вероятностных сеток является целесообразное преобразование одной или обеих прямоугольных координат { х, F (х) } графика функции распределения F (я), проведенное таким образом, чтобы взаимная зависимость обеих новых преобразованных переменных стала линейной.

Издание официальное    Перепечатка    воспрещена

* Переиздание декабрь 1984 г, с Изменением М 1, утвержденным в ноябре 1983 г.; Пост. № 5102 от 31.ld.83JMhLC № 2—84 г.)

© Издательство стандартов, 15>85

где Кх — коэффициент 'масштаба для оси абсцисс (формула

(9));

О А—расстояние точки А от начала координат, мм (см. примечание к п. 3.1.5).

3.2.5.    Оценку параметра X экспоненциального распределения вычисляют по формуле

х= • 6,0000-?,    (22)

Н

где <7 = tga — угловой коэффициент аппроксимирующей прямой.

3.2.6.    Примеры определения статистических характеристик для экспоненциального распределения приведены в справочном приложении 1 (примеры 3 и 4).

3.3. Логарифмически нормальное распределение.

3.3.1. Случайная величина X считается распределенной по логарифмически нормальному закону, если ее функция распределения имеет вид

F{X- (х.аНФр^-)    (23)

для 0<дс<сзо; |Л>0; б>0;

V^д

Ф(у)= ]• <c(v)dv=—^ \ е ² dv.

-L V 2л -L

Таблица 2

Вероятностная шкала для экспоненциального распределения S°y (F) = —501n (\-F) Н=300

F Sy(F) F Зу(П F 0 0 0,52 36,7 0,74 67,4 0,05 2,6 0,54 38,8 0,76 71,4 0,10 5,3 0,56 41,0 0,78 75,7 0,15 8,1 0,58 43,4 0,80 80,5 0,20 11,2 0,60 45,8 0,82 85,7 0,25 14,4 0,62 48,4 0,84 91,6 0,30 17,8 0,64 51,1 0,86 98,3 0,35 21,5 0,66 53,9 0,88 106,0 0,40 25,5 0,68 57,0 0,900 115,1 0,45 29,9 0,70 60,2 0,905 117,7 0,50 34,7 0,72 63,7 0,910 120,4

ГОСТ 11.008-75 Стр. 11 Продолоюение табл. 2

F F s/n F SJLF) 0,915 123,3 0,974 182,5 0,9952 267,0 0,920 126,3 0,976 186,5 0,9954 269,1 0,925 129,5 0,978 190,8 0,9956 271,3 0,930 133,0 0,980 195,6 0,9958 273,6 0,935 136,7 0,982 200,9 0,9960 276,1 0,940 140,7 0,984 206,8 0,9962 278,6 0,945 145,0 0,986 213,4 0,9963 280,0 0,950 149,8 0,988 221,1 0,9964 281,3 0,952 151,8 0,9900 230,3 0,9965 282,7 0,954 154,0 0,9905 232,8 0,9966 284,2 0,956 156,2 0,9910 235,5 0,9967 285,7 0,956 158,5 0,9915 238,4 0,9968 287,2 0,960 160,9 0,9920 241,4 0,9969 288,8 0,962 163,5 0,9925 244,6 0,9970 290,4 0,964 166,2 0,9930 248,1 0,9971 292,2 0,966 169,1 0,9935 251 ,8 0,9972 293,9 0,968 172,1 0,9940 255,8 0,9973 295,7 0,970 175,3 0,9945 260,2 0,9974 297,6 0,972 178,8 0,9950 264,9 0,9975 299,6

Здесь [х — математическое ожидание и а — среднее квадратическое отклонение случайной величины у = lg х.

Вероятностная сетка для логарифмически нормального распределения содержит по оси абсцисс логарифмическую шкалу и по оси ординат значения у, которые обозначают через Ф (у).

3.3.2. Коэффициент масштаба К_х для оси абсцисс вычисляют по формуле

К_х=

1§^тах—IS-^min

(24)

ГДв Z/, Xmln> -К’тах ПО И. 3.1.3.

Величину S_x (х) вычисляют по формуле

SA.x)=K_x-\gx.

Для Кх =100 в табл. 3 приведены значения 5^(л:)= lOOlgA:.

Для К_х¥= 100 величину S_x (х) находят по формуле

(25)

ЗД=-ЙгЗД.

100

(25а)

Стр. 12 ГОСТ 11.008-75

3.3.3.    Величину S_y (F), откладываемую по оси ординат, определяют по формуле (10),

В табл. 1 приведены значения S_y(F)=Sy(F) для случая # = 300 мм; тогда S°_y (Е) = 50 у.

3.3.4.    Если известно, что случайная величина имеет логарифмически нормальное распределение, то на вероятностную сетку для логарифмически нормального распределения наносят точки по формулам (25) и (10). Затем строят прямую.

Если точка А представляет собой точку пересечения прямой с

осью абсцисс, то оценку параметра р, находят по формуле

±ОА К_х ⁹

(26)

где О —! начало координат, О А — расстояние от О до А, измеряемое в миллиметрах.

Примечание. Знак О А в формуле (26) определяют в соответствие с примечанием в п. 3.1.5.

Если начало координат О не помещено на чертеже, то О А вычисляют по формуле

OA=K_x\gx_m-_m+O_xA,    (27)

где 0\ — точка на оси абсцисс, соответствующая x_min; расстояние 0\А измеряют в миллиметрах.

Оценку а параметра а определяют по формуле (14), где К_х. вычисляют по формуле (24).

3.4. Распределение Вейбулла

3.4.1. Случайная величина X распределена по двухпараметрическому закону Вейбулла, если ее функция распределения имеет вид

F(x\a,b)

¹ вхр {    (~

0,

к>0,

х<0,

где а — параметр масштаба, b ■— параметр формы.

Вероятностная сетка для распределения Вейбулла устроена следующим образом. По оси абсцисс —- логарифмическая шкала,, а по оси ординат откладывают значения у и обозначают их через величину F (у).

Значения F (у) вычисляют по формуле

F(y)=l—e-°^y,

где

у=1п[—1п(1—F)].

(28)

(29)

ГОСТ 11.008—75 Стр. 13

3.4.2.    Величину S_x (х) находят по формуле (25), где коэффициент масштаба К_х для оси абсцисс вычисляют по формуле (24), а табл. 3 применяют по п. 3.3.2.

3.4.3.    Для выбора масштаба по оси ординат задаются

/w-0,999.

Тогда Ут\п=—6,91, Утах= +1,93, а размах величины у равен 8,84.

Величину S_y (F) вычисляют по формуле

³^= -or V.    (ЭД

где у определяется по формуле (29),

Длина шкалы по оси ординат Н — 300 мм соответствует S_y (F) =S°_y (F) =33,94 у (табл. 4).

Для длины шкалы #=+300 мм величину S_y (F) вычисляют по формуле (12), в которой S°_y (F) берут из табл. 4.

3.4.4.    Если исследуемая случайная величина X подчиняется двухпараметрическому распределению Вейбулла, то на вероятностную оценку для распределения Вейбулла (справочное приложение 2, черт. 3, см. бандероль) наносят точки по формулам (25) и (30). Затем строят прямую наиболее близкую к этим точкам.

Если точка А является тачкой пересечения этой прямой с осью

абсцисс, то оценку параметра масштаба а определяют из уравнения

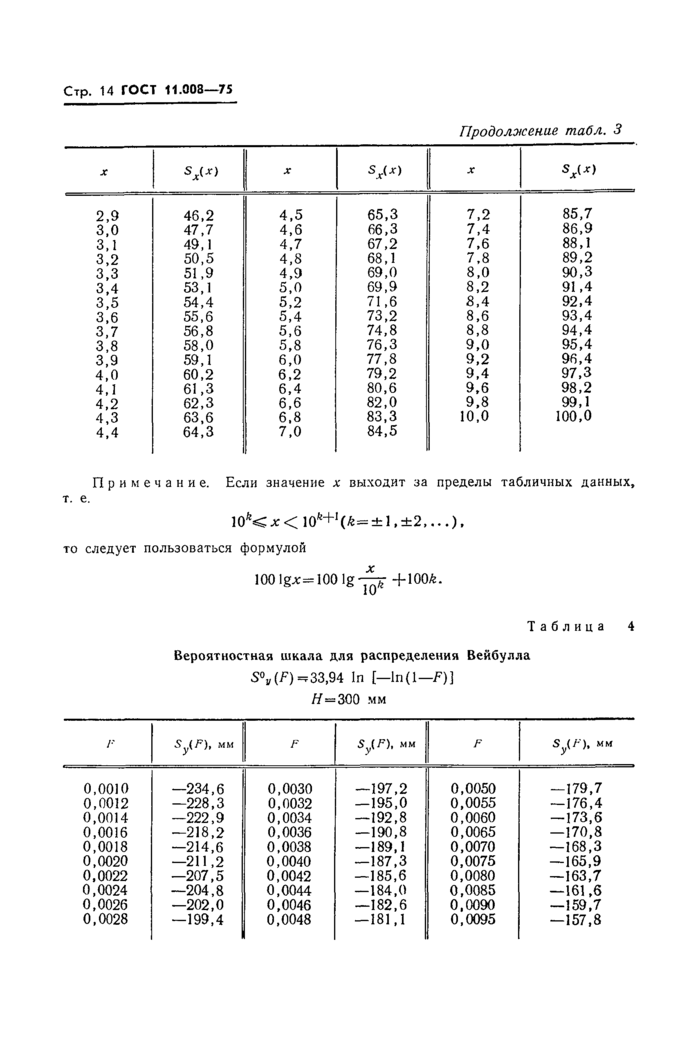
Продолжение табл. 3

X Sjx) X S^(*> X Sx(x) 2,9 46,2 4,5 65,3 7,2 85,7 3,0 47,7 4,6 66,3 7,4 86,9 3,1 49,1 4,7 67,2 7,6 88,1 3,2 50,5 4,8 68,1 7,8 89,2 3,3 51,9 4,9 69,0 8,0 90,3 3,4 53,1 5,0 69,9 8,2 91,4 3,5 54,4 5,2 71,6 8,4 92,4 3,6 55,6 5,4 73,2 8,6 93,4 3,7 56,8 5,6 74,8 8,8 94,4 3,8 58,0 5,8 76,3 9,0 95,4 3,9 59,1 6,0 77,8 9,2 96,4 4,0 60,2 6,2 79,2 9,4 97,3 4,1 61,3 6,4 80,6 9,6 98,2 4,2 62,3 6,6 82,0 9,8 99,1 4,3 63,6 6,8 83,3 10,0 100,0 4,4 64,3 7,0 84,5

Примечание. Если значение х выходит за пределы табличных данных,

т. е.

10*<л:< 10^fe+¹(^=±l.±2,...).

то следует пользоваться формулой

100 lgA:=100 lg-—_F+100^.

Таблица 4

Вероятностная шкала для распределения Вейбулла S°_y (F) =?33,94 In [—In (1—F)]

H — 300 мм

F	MM	F	Sy{F), мм	F	Sy(F)% мм
0,0010	—234,6	0,0030	—197,2	0,0050	-179,7
0,0012	—228,3	0,0032	—195,0	0,0055	—176,4
0,0014	—222,9	0,0034	—192,8	0,0060	-173,6
0,0016	-218,2	0,0036	—190,8	0,0065	-170,8
0,0018	—214,6	0,0038	—189,1	0,0070	—168,3
0,0020	—211,2	0,0040	—187,3	0,0075	—165,9
0,0022	—207,5	0,0042	—185,6	0,0080	—163,7
0,0024	—204,8	0,0044	—184,0	0,0085	—161,6
0,0026	—202,0	0,0046	—182,6	0,0090	—159,7
0,0028	—199,4	0,0048	—181,1	0,0095	—157,8

ГОСТ 11.003-75 Стр. 15 Продолжение табл. 4

F Sy(F). ММ F Sy{F)t мм F Sy(F), мм 0,010 —156,2 0,075 —86,6 0,5000 -12,4 0,012 —149,9 0,080 —84,3 0,5400 -8,6 0,014 —144,7 0,085 —82,2 0,5800 -4,8 0,016 —140,1 0.090 —80,1 0,6200 -1,1 0,018 —136,0 0,095 —78,2 0,6321 0,0 0,020 —132,4 0,100 —76,4 0,6600 Ь2,6 0,022 —129,2 0,120 —69,8 0,7000 Ь6,2 0,024 —126,2 0,140 -64,2 0,7400 Н0,1 0,026 —123,4 0,160 —59,3 0,7800 Ь14,1 0,028 —120,9 0,180 —54,9 0,8200 1-18,3 0,030 —118,5 0,200 —50,9 0,8600 [-22,9' 0,032 —116,3 0,220 —47,3 0,9000 [-28,3 0,034 —114,2 0,240 —43,9 0,9250 Ь32,3 0,036 —112,2 0,260 —40,7 0,9500 Ь37,2 0,038 —110,3 0,280 —37,8 0,9600 Ь39,7 0,040 —108,6 0,3000 —35,0 0,9700 г 42,6 0,042 —106,9 0,3200 -32,3 0,9800 L46,3 0,044 —105,3 0,3400 —30,1 0,9900 [-51,8 0,046 —103,7 0,3600 —27,4 0,9925 [-53,9 0,048 —102,2 0,3800 -25,0 0,9950 Ь56,6 0,050 —100,8 0,4000 —22,8 0,9960 Ь57,7 0,055 —97,5 0,4200 —20,6 0,9970 [-59,7 0,060 —94,4 0,4400 —18,6 0,9980 [-62,0 0,065 0,070 —91,2 —89,1 0,4600 0,4800 —16,4 —14,4 0,9990 [-65,4

где ОА —расстояние точки А от начала координат О.

Примечание. Знак перед О А в формуле (31) определяет в соответствии с примечанием в п. 3.1.5. Если начало координат О не помещено на чертеже, то О А вычисляют по формуле (27).

Оценку параметра масштаба а можно также определить с помощью табл. 3 по формуле

S°(a)=    •    100.    (32)

Кх

Оценку Ь параметра формы b вычисляют по формуле

£=3,84-^- -q,    (33)

где К_х — вычисляют по формуле (24),

<7 = tga — угловой коэффициент аппроксимирующей прямой, Н—'Длина шкалы по оси координат.

Для шкалы по оси ординат длиной # = 300 <мм формула (33) примет вид

b = ~^q.    (34)

78,1 ⁷

Разд. 3 (Измененная редакция, Изм. № 1).

Разделы 4, 5, 6 и 7 (Исключены, Изм. № 1).

ПРИЛОЖЕНИЕ 1 Справочное

ПРИМЕРЫ ПРИМЕНЕНИЯ ПРАВИЛ СТАНДАРТА

Пример 1. На опыте получена выборка объемом п—100. Значение элементов выборки приведены в табл. 1.

Таблица 1

*1 Х1 Х1 Х1 +46 +20 +168 + 128 +6 +16 —15 —14 +149 +227 +60 —89 +102 +4 —90 +19 +139 —113 —116 —20 +91 +77 —26 +245 +118 +38 —36 —53 —150 —51 + 183 —63 —69 +29 +53 +128 +137 +103 —206 +5 —48 —133 —201 —52 —138 —29 +118 +1 —101 + 16 —114 —16 —5 —136 +36 —162 +139 +125 —23 +38 —179 + 14 +21 —6 —10 —253 +27 +136 —134 —35 +61 —92 + 104 +47 —31 +1 +28 —55 —210 —91 —180 —51 +8 —124 —119 —105 —166 —138 +66 —49 —34 —96 —44 +76 —52 —73 —140 +22 +299 +72

Производим группировку и подсчет точек.

Выбираем х*——260, ***=300, л:** —**=560. Разбиваем интервал [—260, 300] на 44 интервалов длины А=40. Для подсчета nj составляем табл. 2.

ГОСТ 11.008-75 Стр. 17

Подсчет tij производится следующим образом (п. 2.1.4): перебирают элементы выборки и когда в /-й интервал попадает элемент, то в /-й строке табл. 2 ставят штрих. Если элемент выборки совпадает с границей /-го и (/-И)-го интервалов, /—1,2, . . , Ы, то в /-й и в (/ +1)-й строках ставят штрихи половинной длины. Каждый пятый штрих в строке перечеркивает предыдущие четыре, если он не соответствует границе интервала; в этом случае ставят вертикальный штрих половинной длины.

Таблица 2

Номер Интервал Число Номер Интервал Число интервала группировки точек интервала группировки точек 1 —260, —220 ] 8 +20, +60 12 2 —220, —180 3,5 9 +60, +100 6,5 3 —180, —140 5 10 + 100, +140 12 4 —140, —100 12,5 11 +140, +180 2 5 —100, —60 8 12 + 180, +220 1 6 —60, —20 16,5 13 +220, +260 2 7 —20, +20 17 14 +260, +300 1

Пример 2. В процессе эксперимента получили результаты, которые включи* ли в восемь классов (табл. 3).

Определить оценки параметров т и а нормального распределения.

Таблица 3 Упорядоченные результаты, полученные в процессе эксперимента

1 xi п1 £ i1 i nf F(xn))= 2 — (О ^ л+1 ; = 1 1 20 2 2 0,03 2 40 4 6 0,10 3 60 9 15 0,25 4 80 14 29 0,48 5 100 15 44 0,73 6 120 8 52 0,87 7 140 5 57 0,95 8 160 2 59 0,98

Решение.

Общее число наблюдений /г = 59>30. Поэтому целесообразно использовать группировку данных по п. 2-1.4 (табл. 3).

Точечную оценку эмпирической функции распределения вычислим по фор* муле (7).

Для построения вероятностной сетки выберем L= 140.

Коэффициент масштаба К_х для оси абсцисс вычислим по формуле (9):

	-1
160—20

ГОСТ 11.008—75 Стр. 19

Решение.

Для построения вероятностной сетки выберем длину шкалы по оси ординат Н = 300 мм и ширину графика L—134 мм.

Коэффициент масштаба по оси абсцисс К_х вычисляют по формуле (9), где *тах —*min = 2827—150=2677:

_ ¹³⁴ Кх~ 2677

Значения S_y (F)_> приведенные в табл. 2 настоящего стандарта, откладывают по оси ординат в миллиметрах.

Точечную оценку функции распределения найдем по формуле (1):

74*1) = ~~с\"Г =0.063 и т. д.

После нанесения точек на вероятностную сетку для экспоненциального распределения (справочное приложение 2, черт. 2) построим прямую, проходящую через начало координат (черт. 2, см. бандероль).

Из графика получим значение углового коэффициента аппроксимирующей прямой *7 — 0,93.

Точечную оценку параметра X найдем по формуле (22):

0,05

X =    *6*0,93=9,3.10-4.

Пример 4. При ресурсных испытаниях невосстанавливаемых электронных деталей найдены значения случайной величины x_it которые приведены в табл. 5.

Предполагается, что данная случайная величина подчиняется экспоненциальному закону распределения вероятности со сдвигом (с=^=0).

Найти оценки параметра сдвига с и параметра масштаба X,

Таблица 5 Упорядоченные значения случайной величины

i xi Sx(x)=Kxxit ММ Р{хь) S° {F), мм Syin 1 526 18,4 0,063 3,3 2.2 2 566 19,8 0,125 6,7 4,46 3 664 23,2 0,187 10,5 7 4 673 23,6 0,250 14,4 9.6 5 767 26,8 0,312 18,6 12,4 6 857 30,0 0,375 23,1 15,4 7 1000 35,0 0,437 29,0 19,3 8 1068 37,4 0,500 34,7 23,1 9 1191 41,7 0,563 41,0 27,3 10 1484 51,9 0,625 48,4 32,27 11 1819 63,7 0,687 57,1 38,06 12 2046 71,6 0,750 69,3 46,2 13 2571 90,0 0,812 83,0 55,33 14 3057 107,0 0,875 104,0 69,3 35 4610 161,4 0,937 139,0 92,7

Стр. 2 ГОСТ 11.008-75

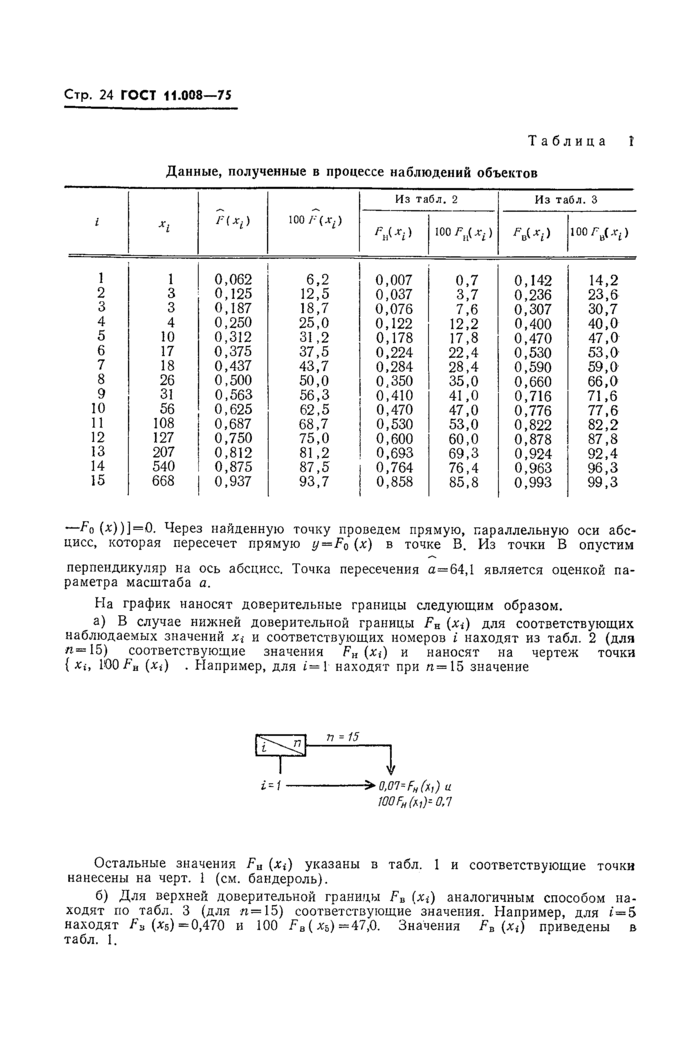
Для выбор™ объемом п из значений случайной величины X на вероятностную сетку для данного вида распределения наносят

точки эмпирической функции распределения F (х). Затем по этим точкам проводят прямую так, чтобы нанесенные точки отклонялись от нее как можно меньше.

1.2.    В табл. 1—4 приведены данные, на основании которых строят вероятностную сетку для каждого из указанных распределений вероятностей. Данные в этих таблицах рассчитаны на длину шкалы 300 мм. С помощью пропорционального расчета можно построить шкалы любых размеров.

1.3.    Вероятностной сеткой пользуются в основном для графического определения оценок параметров распределения.

Одновременно с определением параметров выполняют графическую проверку соответствия эмпирического распределения теоретическому.

1.4.    Если нанесенные эмпирические точки мало отклоняются от проведенной прямой, то это свидетельствует о том, что опытные данные не противоречат тому виду распределения, для которого была построена сетка.

При проведении этой проверки необходимо учитывать, что на концах выборки опытные точки могут больше отклоняться от прямой, чем в средней части графика.

1.5.    Если на вероятностной сетке не получается прямая, то отвергается гипотеза о выбранном виде распределения.

1.6.    Оценки параметров предполагаемого распределения и некоторые статистические характеристики определяют при помощи точек пересечения аппроксимирующей прямой с соответствующими осями координат.

Примечание. Для получения более точных оценок параметров следует использовать ГОСТ 11.004-74, ГОСТ 11.005-74, ГОСТ 11.007-75 и ГОСТ 11.009—79 в зависимости от вида распределения наблюдений.

1.1—1.6. (Измененная редакция, Изм. № 1),

2. ГРАФИЧЕСКАЯ ОЦЕНКА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

2.1.    Точечная оценка функции распределения-

2.1.1.    Основной вероятностной характеристикой случайной величины X является теоретическая функция распределения F (х), информацию о которой дает эмпирическая функция распределения /^(х).

2.1.2.    При проведении прямой по нанесенным точкам (полученным экспериментальным путем) графика эмпирической функции распределения получают графическую оценку теоретической функции распределения F (х).

Стр. 20 ГОСТ 11.008—75

Решение.

Для построения вероятностной сетки выберем шкалу длиной по оси ординат // = 300 мм и ширину графика L=143 мм.

Коэффициент масштаба для оси абсцисс Кх вычисляют по формуле (9), где х_т а х — х_т1п = 4610—526 = 4084:

_к = _У1

^Кх 4084

Значения S°_y (F), соответствующие // = 300 мм, приведены в табл. 2 настоящего стандарта.

Точечную оценку функции распределения определим по формуле (1):

—-— =0,063, и т.д. 16

После нанесения точек на вероятностную сетку (справочное приложение 2> черт. 3) построим прямую (черт. 3, см. бандероль). Из графика определим О А (расстояние точка А от начала координат О) и q (угловой коэффициент аппроксимирующей прямой):

ОЛ = 14 мм; д=0,6\.

Точечную оценку параметра сдвига с найдем по формуле (21):

-    14000

^{С =} 0,035

Точечную оценку параметра X вычислим по формуле (22):

•60,61=6,410-<.

Пример 5. На опыте получена выборка из 15 значений случайной величины,, распределенной по логарифмически нормальному закону. Упорядоченные значения Xi приведены в табл. 6.

Найти оценки параметров _tu и а.

Таблица 6

*1 SJx)=425 Igx 100 F{ Xt) i xi Sx(Jr)=425 Igx 100 p(xt) I 599 1180 6,3 9 1028 1280 56,2 2 648 1195 12,5 10 1055 1285 62,5 3 796 1233 18,7 11 1077 1289 68,7 4 896 1254 25,0 12 1078 1289 75,0 5 905 1257 31,2 13 1126 1297 81,2 6 927 1261 37,5 14 1185 1306 87,5 7 943 1264 43,7 15 1428 1340 93,7 8 1010 1277 50,0

ГОСТ 11.008—75 Стр. 3

2.1.3.    Если объем выборки п не превосходит 30, исходными данными являются величины х\, хг, х₃, . . . , х_п. Эти величины соответствуют значениям исследуемой случайной величины X, полученным при независимом наблюдении случайной выборки объемом п. Предполагается, что величины Xi расположены в порядке неубывания, так что справедливы следующие неравенства

x_t<x₂< . . . <х_л, тогда оценку F (х<) находят по формуле

— (1)

2.1.4.    Если объем выборки п>30, рекомендуется применять группировку данных. Выбирают числа х* их** так, чтобы

х** ^x_max, и интервал [х*, х**] разбивают на k классов равной длины ft, где

h—    .    (2)

k    ⁴

Величины х* и х** рекомендуется выбирать так, чтобы значение ft, найденное по формуле (2), было удобным для вычислений (см. приложение 1, пример 1).

Число точек в /чм классе (/=1, . . . , k) обозначают щ:

для 30<п^200 принимают значения

7<ft<20;    (3)

для 200<п<1000 принимают значения

20<£<40.    (4)

Примечание. Если внутрь /-го класса попало п'з точек, а внутрь (у-И)-го — n'j+i точек выборки, причем на границу этих классов попало / точек выборки, то полагают:

, I

-у •    (⁵)

";+i^=ra;+i + Y •

Таким образом, из точки на границе классов в смежные классы относят по У₂ точки.

2.1.5.    После группировки данных эмпирическую функцию распределения в точках, соответствующих серединам классов, оценивают по формуле:

Стр. 4 ГОСТ 11.008-75

где х_(т>— середина m-го класса,

яг=1,2,..., к;

k — число классов равной длины; щ — частота в /-ом классе (определяется по п. 2.1.4).

2.2. Точечная оценка статистических характеристик

2.2.1. На построенной для определенного распределения вероятностной сетке, содержащей нанесенные точки {х_г*, F (х*) } при

п^ЗО (н. 2.1.3) и { x_(m), F U(m))} при п>30, (п. 2.1.5), проводят прямую y~F₀(x), наилучшим образом приближающуюся к этим точкам.

Статистические характеристики оцениваются следующим образом.

На шкале х выбирают определенное значение х*, которое представляет собой абсциссу точки на прямой y=F₀ (х). Оценкой значения функции распределения jF₀ (я*) является ордината рассматриваемой точки прямой (см. чертеж).

{xi, F (я*)}—нанесенные точки графика эмпирической функции распределения; y=F₀ (х) —прямая, проведенная по точкам;

х*—*вьгбранное определенное значение;

F₀ (х*)—оценка функции распределения (ню выбранному определенному значению х*);

F₀ (х_р)=р— выбранное определенное значение;

х_р—оценка 100 р %'-ной квантили.

2.2.2. При оценке 100 р %-ной квантили на оси ординат (см.

чертеж) выбирают определенное значение F₀ (х_р) — р и на оси

ГОСТ 11.003-75 Стр. 5

абсцисс находят соответствующее значение х_р. Оценкой 100 р

%-ной [квантили является значение х_р.

Разд. 2 (Измененная редакция, Изм. № 1).

3. ПОСТРОЕНИЕ ВЕРОЯТНОСТНЫХ СЕТОК И ОЦЕНКА ПАРАМЕТРОВ И СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ДЛЯ ОСНОВНЫХ ВИДОВ РАСПРЕДЕЛЕНИЙ

3.1.    Нормальное распределение

3.1.1.    Случайная величина X считается распределенной по нормальному закону, если ее функция распределения имеет вид

F(x,m,a)=(8)

где

Ф{у)= \ y(v)dv = • -¹ — г е ² dv,

-со    V    -оо

х—т    .    .    ,

причем У⁼ —“— Д^ля— ⁰⁰ <-^< + оо;

m — среднее значение;

а—'Среднее квадратическое отклонение.

Вероятностная сетка для нормального распределения содержит на оси абсцисс равномерную шкалу и по оси ординат значения у, которые пропорциональны квантилям нормированной центрированной функции нормального распределения (черт. 1, справочное приложение 2, см. бандероль).

3.1.2.    Принимаем, что S_x (х) обозначает абсциссу точки, соответствующей значению х, и S_y (F) •— ординату точки, соответствующей значению F.

$х (X)

Отношение - постоянно,    называется    коэффициентом

масштаба и обозначается К_х-

3.1.3.    Коэффициент масштаба К_х для оси абсцисс вычисляют по формуле

К_х=---,    (9)

•^max -^mln

где L— ширина графика, мм;

*тах> x_min— соответственно наименьший и наибольший элемент выборки

Примечание. В этом и носледуклцих иедразделах величину L следует выбирать в миллиметрах так, чтобы значение вычисляемого коэффициента К_х было удобным для остальных вычислений.

2—654

Стр. 6 ГОСТ 11.008-75

3.1.4. Для выбора масштаба по оси ординат задаются

Дшш-0,0013, F_тах=0,9987.

В случае нормального распределения им соответствуют значения

Уш1п = -3,000, Ушах=+3,000,

а величину S_y (F), откладываемую по оси ординат в миллиметрах, вычисляют по формуле

S    ^Н V,    (Ю)

У^к‘ ’    6,0000^У’

где Н — длина шкалы но оси ординат (в миллиметрах), т. е. высота графика;

y=U_p(F)— квантиль нормированного центрированного нормального распределения, соответствующая значению F. Если Д=300 мм, то S°_y (F) =50 у = 50 U_p (F). Значения 5° (F) в зависимости от F для этого случая приведены в табл. 1. Для ЕС0,5 применяют формулу

^(Е)=-^(1~+).    О    В

Таблица 1 Вероятностная шкала для нормального распределения Н=300

F У S°(n, мм F У Sy{F), мм 0,50 0,00 0,0 0,79 0,80 40,0 0,52 0,05 2,5 0,80 0,85 42,5 0,54 0,10 5,0 0,82 0,90 45,0 0,56 0,15 7,5 0,83 0,95 47,5 0,58 0,20 10,0 0,84 1,00 50,0 0,60 0,25 12,5 0,85 1,05 52,5 0,62 0,30 15,0 0,86 1,10 55,0 0,64 0,35 17,5 0,87 1,15 57,5 0,66 0,40 20,0 0,88 1,20 60,0 0,67 0,45 22,5 0,89 1,25 62,5 0,69 0,50 25,0 0,903 1,30 65,0 0,70 0,52 26,0 0,912 1,35 67,5 0,71 0,55 27,5 0,919 1,40 70,0 0,73 0,60 30,0 0,927 1,45 72,5 0,74 0,65 32,5 0,933 1,50 75,0 0,76 0,70 35,0 0,939 1,55 77,5 0,77 0,75 37,5 0,945 1,60 80,0

ГОСТ 11.008-75 Стр. У Продолжение табл. 1

F У S°(F), мм F У мм 0,951 1,65 82,5 0,992 2,40 120,0 0,955 1,70 85,0 0,993 2,45 122,5 0,960 1,75 87,5 0,9938 2,50 125,0 0,964 1,80 90,0 0,9946 2,55 127,5 0,968 1,85 92,5 0,9953 2,60 130,0 0,971 1,90 95,0 0,9960 2,65 132,5 0,974 1,95 97,5 0,9965 2,70 135,0 0,977 2,00 100,0 0,9970 2,75 137,5 0,980 2,05 102,5 0,9974 2,80 140,0 0,982 2,10 105,0 0,9978 2,85 142,5 0,984 2,15 107,5 0,9981 2,90 145,0 0,986 2,20 110,0 0,9985 2,95 147,5 0,988 2,25 112,5 0,9987 3,00 150,0 0,989 2,30 115,0 0,991 1 2,35 117,5

Примечание. Для Д<0,5: (F) = -Sy(\-F).

Для длины шкалы Н=?ь300 мм величину S_y (F) вычисляют по формуле

^Sy^{F)= ~Ш ^S°^(F)’    ⁽¹²⁾

где S_y (F)—значение ординаты точек F для шкалы с произвольной длиной Я, м-м;

S°_y (F)—значение ординаты точек F для шкалы длиной Я = 300 мм (табл. 1), мм.

3.1.5. После нанесения значений точечных оценок функции

распределения F (Xi) строят график прямой F₀ (х) (п. 2.2.1).

Оценку параметра т (среднего значения) определяют при помощи абсциссы точки А на прямой по формуле

1 О А    /1 о\

т=±——,    (13)

*\Х

где О—начало координат;

А — точка пересечения прямой с осью абсцисс.

Примечание. В формуле (1:3) ОА — расстояние от точки О до точки А, мм; расстояние ОА берется со знаком «плюс», если точка А лежит правее точки О на оси абсцисс, и со знаком «минус», если она лежит левее, т. е. соответствует отрицательной абсциссе.

2*

Стр. 8 ГОСТ 11.008-75

Если начало координат О не помещено на чертеже, то ОА вычисляют по формуле

ОА—/C^_min+OiA,    (13а)

где 01 — точка на оси абсцисс, соответствующая x_min; расстояние 0\А измеряют в миллиметрах.

Ордината указанной точки А соответствует S_y(F)~y=^0 [F=0,50].

Оценку параметра а (среднего квадратического отклонения) вычисляют по формуле

Н _т J_ 6,00/G ’ ч ’

где q — угловой коэффициент аппроксимирующей прямой. Для // — 300 используют формулу

50 J_ Кх' ч '

3.1.6. Допускается другой способ определения оценки параметра т — не по F₀ (л;), а поF (х). При этом т определяют из условия jF(atz)=0i5 или 100F (т)=50 илиже£/_р (F (т))=0 (в качестве А в формуле (13) рассматривают точку пересечения F (я) с осью абсцисс).

Оценку а вычисляют по формуле

а = т—х_и    (16)

где х\ — оценка абсциссы прямой, для которой справедливо ^o(^i)=Oj1587 или ЮО/^Н 15,87 или U_p= — 1.

Оценку среднего квадратического отклонения вычисляют также но формуле

о = х₂— т,

где для х% справедливо

/^(лгз)—0,8413 или 100/⁷0(х_!)==84,13, или 6^= + 1.