ГОСТ 11.007-75
Прикладная статистика. Правила определения оценок и доверительных границ для параметров распределения Вейбулла
Купить ГОСТ 11.007-75 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Устанавливает правила определения оценок и доверительных границ для параметров распределения Вейбулла по совокупности статистических (опытных) данных, полученных на производстве в процессе измерений, испытаний и анализов, если эти опытные данные подчиняются распределению Вейбулла.
Переиздание. Ноябрь 1977 г.
Отменен без замены
Оглавление
1. Общие понятия и положения
2. Оценка параметра масштаба a при известном значении параметров формы b и сдвига c (случай [a])
3. Оценка параметра масштаба a и формы b при известном значении параметра сдвига c (случай [a, b])
4. Оценка параметра масштаба a и сдвига c при известном значении параметра формы b (случай [a, c])
5. Оценка параметра масштаба a, формы b и сдвига c (случай [a, b, c])
6. Правила определения доверительных границ для параметра масштаба a при известном значении параметров формы b и сдвига c (случай [a])
7. Правила определения доверительных границ для параметров масштаба a и формы b при известном значении параметра сдвига c (случай [a, b])
Приложение 1 (рекомендуемое) Оценка параметров распределения Вейбулла методом максимального правдоподобия
Приложение 2 (справочное) Примеры применения правил стандарта
Приложение 3 (справочное) Условные обозначения, употребляемые в стандарте
Приложение 4 (справочное) Теоретические основы стандарта
Литература
| Дата введения | 01.07.1976 |
|---|---|
| Добавлен в базу | 01.01.2019 |
| Завершение срока действия | 01.03.1987 |
| Актуализация | 01.01.2021 |
Организации:
| 05.09.1975 | Утвержден | Государственный комитет стандартов Совета Министров СССР | 2347 |
|---|---|---|---|
| Издан | Издательство стандартов | 1978 г. |
Applied statistics. Point and interval estimators for parameters of Weibull distribution
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8
стр. 9
стр. 10
стр. 11

стр. 12
стр. 13

стр. 14

стр. 15

стр. 16
стр. 17

стр. 18

стр. 19

стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26

стр. 27

стр. 28

стр. 29
стр. 30
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРИКЛАДНАЯ СТАТИСТИКА
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СТАНДАРТОВ СОВЕТА МИНИСТРОВ СССР
Москва
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА
Издание официальное
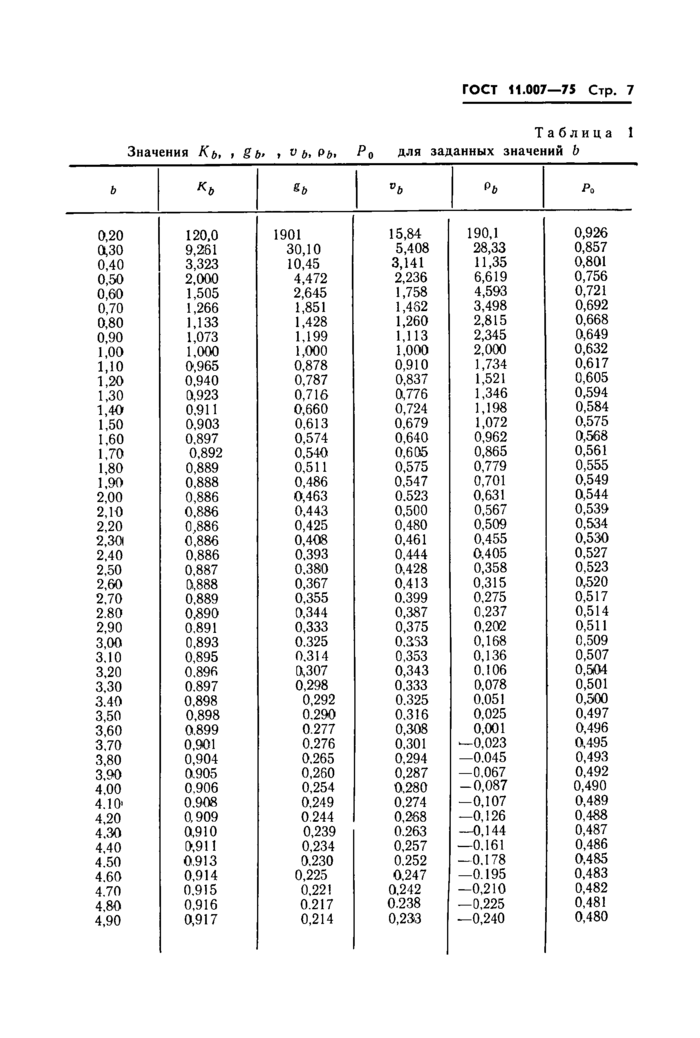
ГОСТ 11.007-75 Стр. 9
|
Продолжение табл. 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
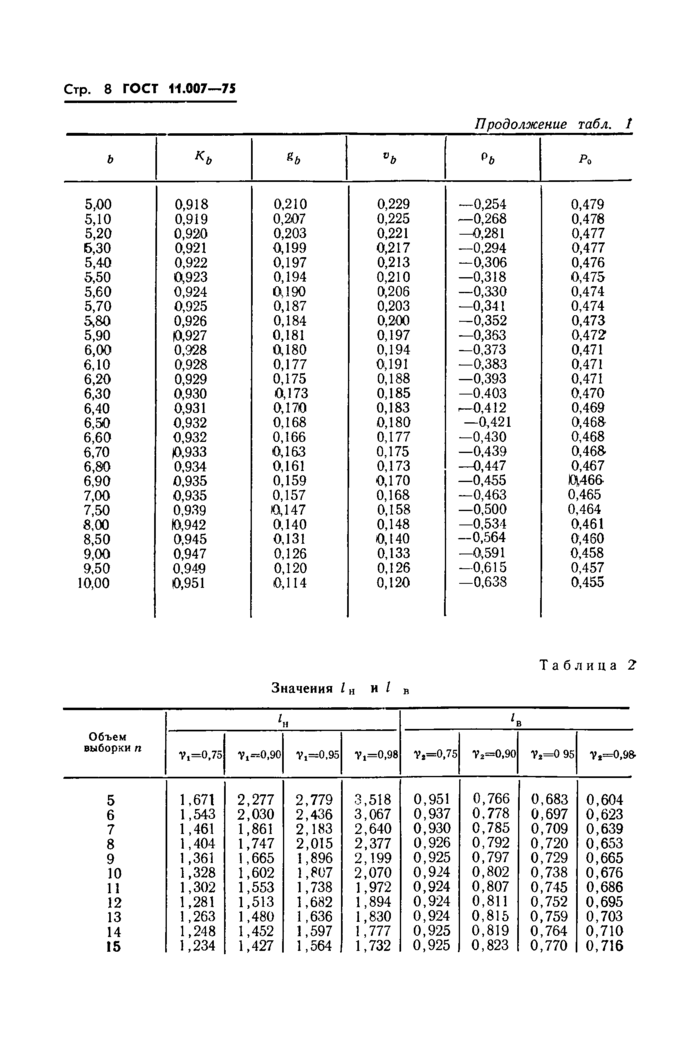
Op. 10 ГОСТ 11.007-75
|
Значения |
| ||||||||||||||||||||||||||||||||||||||
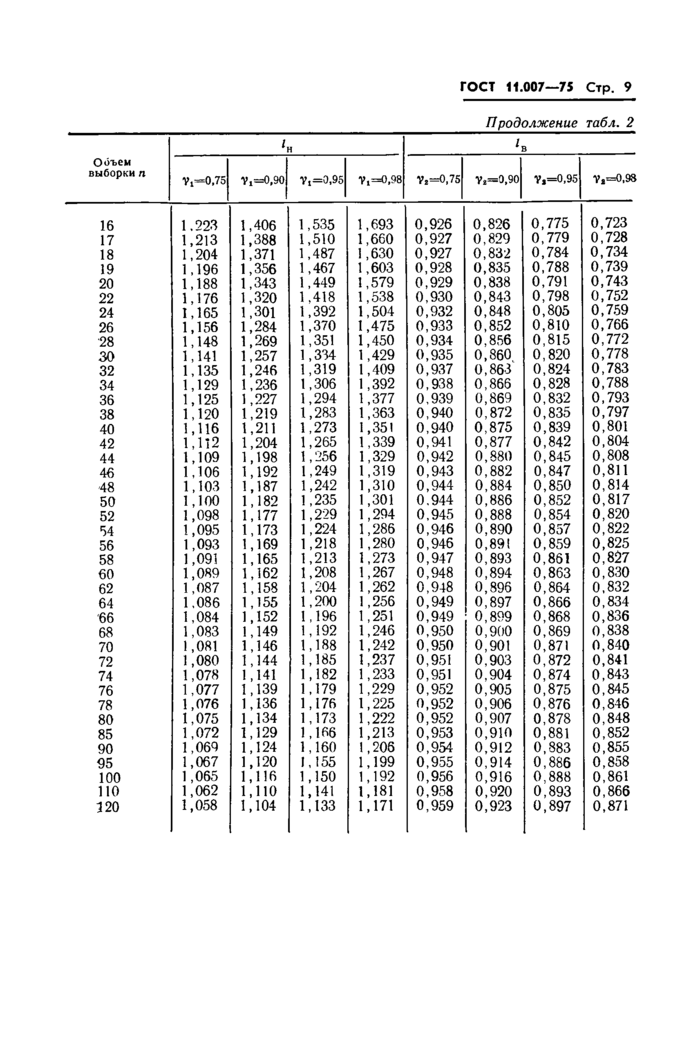
ГОСТ 11.007-75 Стр. 11
|
О СП сГ |
00-^0с0000с0о001''--10см0а010с0а0т^сг>с00с0
OOOOOOOb-r'^l''-t''--CO<OCOcOlOLOlO^''t,COCOCMCM
со
!=r
К
п
\о
со
н
?•
1Л
г-
o'
?-
т^СМОООО^сМ’—1idGOtOtA’^CO’—'C^QOlOCOi—• Г"- ’'f oOocr>a>o^ajoioooogpQDoocooo®bh-Nh-co<£) ^ °„0„0 2 0 Ooooos OO OOO^CSOO Cf o' o' О o' o' о d o’ o' o' o' o' О o' o'" о о о' о о" о"
I I I I I II I I 1 и I I I I I II I II
QO-HlOO)CON(NN(No0^05(D(MOOlOCOCi(N(D^lO (NC^-.OOa)0)OOoOh-NOtOtDWWTt'COCO(N^O « CO CO 00 СО СЧ « N « w CM CM CM CM CM CM CM CM CM CMCM CM^
o' o' o' o' o' o' o' o' o' O' o' o' o' o' o' o' o' o' o' o' o' o'
«NcOOOCOO)lO-OO^^OOlCC)CDNOLOCDlCCDffi Ю'^’^СОСОСМСМСМ^—'гнОООСО)СоО^ЬСОЮ CM^CN CM CM CM CM 04 CM CM CM CM CM CM <N ~ ~ ~ ~ ^
o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o'
lOMN't^S^^aiCD't^OlMnfOflOCOClCDCfO
OCiOOOOooNSNCOCDcDCOlOlOlClO^TfCQCOOlIN
?•
о о' о' о' о' о' о' о' о' о о' о' о о' о' о' о' о' о' о' о' о
ia
?-
^Cibcp'tCN^C500biO'tCO(N^ONiOW^N^ 00501®CO)C)OOOOCDOOOOC£)OOOOOONNNbtnCD — OoOOOoOOOOOOOOOOOOOOO
o' o' Q o' q' о' о о о' о' о о' о о' о о о' о' о о о' о'
|
СП |
со |
|
СП |
см |
|
о |
со |
|
см" | |
|
QO |
■'f |
|
СП |
ю |
|
о" |
Ол |
|
см' | |
|
lo |
ю |
|
СП | |
|
о“ |
со |
|
f—( | |
|
g |
см СО |
|
о |
см^ |
|
ю | |
|
из |
г- |
|
t- |
со |
|
о' |
о" |
|
?• | |
|
> |
3 |
Е К а» м
£§•
Оо
go о ■ см
lOUjlOlOlOtbtDtO(D0NNNNSoOOO^O)^-H^
Стр. 12 ГОСТ 11.007-75
7.5. Определение верхней доверительной границы для параметра а при неизвестном значении параметра Ь и известном значении с осуществляется следующим образом:
задают одностороннюю доверительную вероятность у2 и вычисляют корни b и а уравнений (1) и (2) приложения 1;
по заданному объему выборки п (5<п<120) и значению у2 из табл. 3 находят значение коэффициента zB;
определяют верхнюю доверительную границу для параметра а по формуле
при значении объема выборки п> 120 значение гв определяют по формуле
(21)
где Uy2 — приведено в табл. 4.
7.6. Определение доверительного интервала для параметра а при неизвестном значении параметра b и известном значении с осуществляют следующим образом:
задают доверительную вероятность у* и односторонние доверительные вероятности Уи и ?2 таким образом, чтобы у*, Yi и у2 удовлетворяли соотношению (13);
для односторонней доверительной вероятности у{ согласно п. 7.4 определяют нижнюю границу он;
для односторонней доверительной вероятности у2 согласно п. 7.5 определяют верхнюю доверительную границу ав;
нижняя ан и верхняя ав доверительные границы образуют доверительный интервал для параметра а при доверительной вероятности y* = Уь+Уг—1 (см. приложение 2, примеры 6, 8).
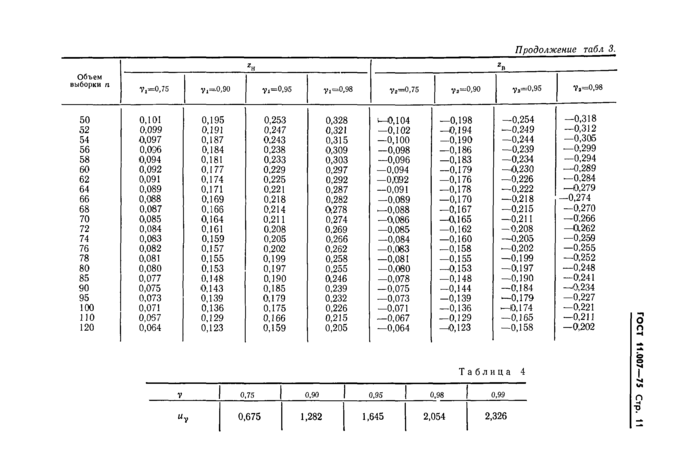
ГОСТ 11.007-75 Стр. 13
ПРИЛОЖЕНИЕ / Рекомендуемое
ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
1. Метод максимального правдоподобия применяется, когда имеются повышенные требования к эффективности оценок.
Случай [а, Ь]. Оценка параметров масштаба а и формы b при известном значении параметра сдвига с по методу максимального правдоподобия осуществляется путем решения системы уравнений
п
«2 (•*<—'c)b\n(xt—,с) п
JL— —----Ь2'п(^)=0> (1)
1 = 1
а -
(2)
Решение уравнения (1) данного приложения осуществляется методом последовательных приближений (методом Ньютона — Рафсона) по рекуррентной формуле
Л А
bk+i=bk +
(3)
S1=2 ln (-*«—c). (4)
(=1
4fe)=2(x~c) h ’ (5)
n A
^=2^-c) (6)
{=1
n /ч
S4fc)=2(Jf‘—b<i'ln2 (A—Ic).
i=1
(7)
Ьк — k~e приближение к корню b уравнения (1) данного приложения,
Ь0 — начальное приближение к корню b уравнения (1) данного приложения.
2. В качестве начального приближения может быть взято значение оценки Ь, полученной методом моментов, или значение оценки параметра 5, полученной с помощью вероятностных сеток (по ГОСТ 11.008-74), или значение оценки параметра Ь, полученной по значению вероятности Р0 с помощью табл. 1.
Я0=Вер{л:<Т}. (8)
Оценка вероятности Pq осуществляется по накопленной частости
(См. приложение 2, пример 8).
3. Чтобы получить несмещенную оценку b для параметра Ь, следует ум-
ножить значение корня b на коэффициент £(п), приведенный в таблице данного приложения.
Оценка а параметра а получается из уравнения (2) данного приложения,
в которое вместо значения b подставляется значение b (см. приложение 2, пример 6).
|
Значения В (п) для получения несмещенной оценки параметра формы b | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. Случай [а, с]. Оценка параметра а и с при известном значении параметра b~bQ по методу максимального правдоподобия осуществляется следующим образом:
— если значение \0<Ь0<2, то в качестве оценки параметра с берут минимальное значение хп(\) из наблюденных значений хи х3, . . хп;
— вычисляют оценку параметра а по формуле
(10)
(См. приложение 2, пример 9).
ГОСТ 11.007-75 Стр. 15
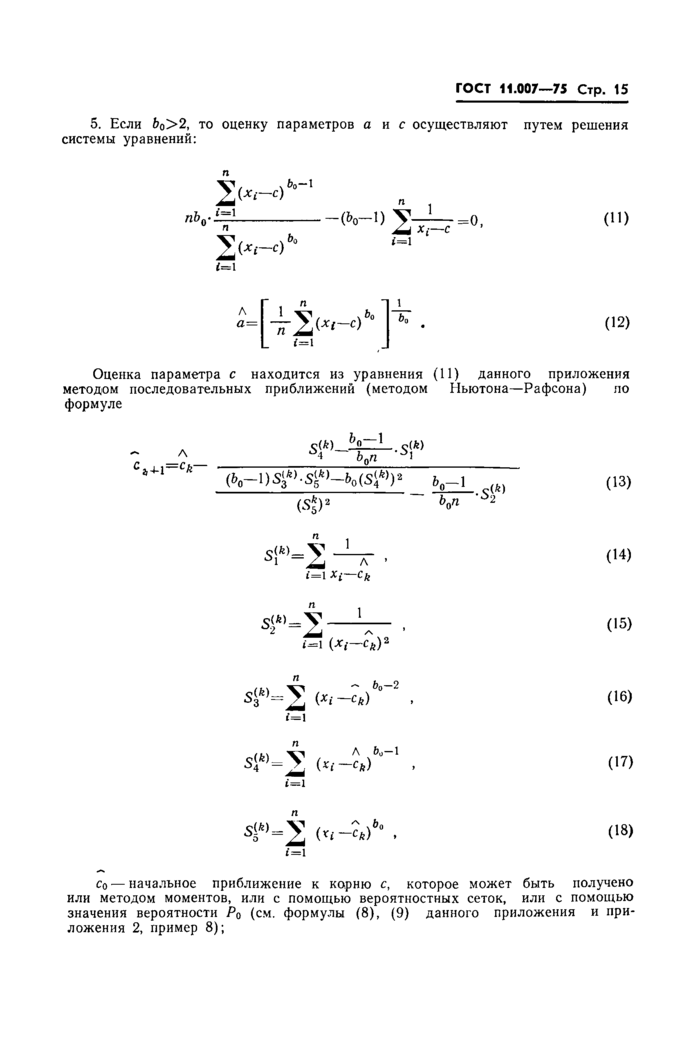
5. Если Ьо>2, то оценку параметров а и с осуществляют путем решения системы уравнений:
Ьо-1
пЪ0-
ы
i=1
(И)
L f=i
bo
bo
(12)
Оценка параметра с находится из уравнения (11) данного приложения методом последовательных приближений (методом Ньютона—Рафсона) по
формуле
~ л
сг)4-1=ск'
sf>-
Ь 0-1
' ь0п
■S\k)
(b0~l)S^-Slk)~b0(Sik>)2 b,
(St)
b0n
"SP
(13)
s
|
k\2 | |
|
<ft) 1 | |
(14)
t=l Cfc
4*’-2
1
(xi ck)2
(15)
4^=2 ^~Ck)b° 2 - (16>
i=1
/L\ Ж’I A b0 1
si*>=2 (*<-<*) . (17>
t=l
si*>=2 (4-V". 08)
1=1
Co — начальное приближение к корню с, которое может быть получено или методом моментов, или с помощью вероятностных сеток, или с помощью значения вероятности Р0 (см. формулы (8), (9) данного приложения и приложения 2, пример 8);
по полученному значению с=с и данному значению Ь0 согласно формуле (12) данного приложения находят оценку для параметра а (см. приложение 2, пример 10).
6. Случай [а, Ь, с]. Оценка параметров а, b, с распределения Вейбулла по методу максимального правдоподобия осуществляется путем решения системы уравнений:
ь—1
=0.
(19)
У (х£—с)*
t=l
t=i
In (jct*—с)
п i=1
(Xi—c)b In (X{—c)
=0
(20)
У(Xr-c)» i-1
a=
-2 <*->■
*=i
(21)
Решение системы уравнений (19), (20), (21), осуществляется следующим образом:
согласно п. 2 данного приложения находят начальное приближение для оценок параметров а, Ь, с.
Если окажется, что начальное приближение оценки параметра b не более 2, то в качестве оценки параметра сдвига берут наименьшее значение хп (1) из наблюденных значений хи х2, . . хп.
Затем из уравнения (20) методом последовательных приближений (методом Ньютона—Рафсона) находят оценку для параметра b по формулам (3)—(7) данного приложения, где вместо значения с следует подставлять значение хп (1) (см. приложение 2, пример 11).
ГОСТ 11.007—75 Стр. 17
ПРИЛОЖЕНИЕ 2 Справочное
ПРИМЕРЫ ПРИМЕНЕНИЯ ПРАВИЛ СТАНДАРТА
|
Таблица 1 Значения xt | ||||||||||||
|
Пример 1. Дано 10 наблюдений случайной величины X, подчиняющейся распределению Вейбулла с известными значениями параметров формы Ь=2 и сдвига с—2. Найти оценку для параметра масштаба а. Результаты наблюдений приведены в табл. 1 данного приложения.
Решение. Согласно формуле (2) получают:
2
=9,13.
Г 10
Пример 2. Дано 100 наблюдений случайной величины, подчиняющейся распределению Вейбулла, если известно, что параметр сдвига с=0.
Результаты наблюдений, расположенные в порядке возрастания (вариационный ряд), приведены в табл. 2 данного приложения. Найти методом моментов оценки для параметров формы b и масштаба а.
|
Таблица 2 Значения х i | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Продолжение таблч 2 | |||||||||||||||||||||||||||||||||||
|
Решение. Согласно формулам (3), (4) и (5) вычисляют
1 100
-Tool *‘-=!'034,
i=1
|
s= |
(я*—*)2 =0,874, | |
|
i=1 | ||
0,874 Vf}~\ ,034
=0,845.
Из табл. 1 находят, что для 6=1,10 v = 0,910, а для 6=1,20 vb =0,83?. Применяя линейную интерполяцию:
6Х — 1,10; vbl =0,910;
Ъ= ; оь=0,Ш;
Ъ2 — \ ,20; vb2 =0,837,
получают
. , Щ-Ьъг Vb2-bb 1,20(0,845-0 910) 1,10(0,837-0,845)
Vb2 —vbi +%&2 — vbl - 0,837—0,910 + 0,837—0,910
С помощью табл. 1 и используя линейную интерполяцию, получают значение кь;
6^1,10; Кьг =0,965;
6 = 1,19; Кь= ;
Ь2= 1,20; Кьг =0,940.
Кь=0,940
(1,19—1,10)
1,20—1,10
+0,965
(1,20-1,19)
1,20—1,10
=0,942.
Согласно формуле (6) находят оценку для параметра масштаба а
1,034 а~0,942 ~1,10'
Таким образом оценки для параметров а и 6 следующие:
а= 1,10; 6=1,19.
УДК 658.562.012.71083.74J Группа Т59
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
Прикладная статистика ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА
Applied statistics. iPioint and interval estimators for parameters of weibull distribution
Постановлением Государственного комитета стандартов Совета Министров ССОР от 5 сентября 1975 г. № 2347 срок введения установлен
с 01.07. 1976 г.
Настоящий стандарт устанавливает правила определения оценок и доверительных границ для параметров распределения Вей-булла по совокупности статистических (опытных) данных, полученных на производстве в процессе измерений, испытаний и анализов, если эти опытные данные подчиняются распределению Вейбулла.
1. ОБЩИЕ ПОНЯТИЯ И ПОЛОЖЕНИЯ
1.1. Правила и положения данного стандарта устанавливаются для распределения Вейбулла, задаваемого плотностью распределения:
/(*, а, Ь, с)= |— (—' “ , если х>с (1)
( 0, если x<ic,
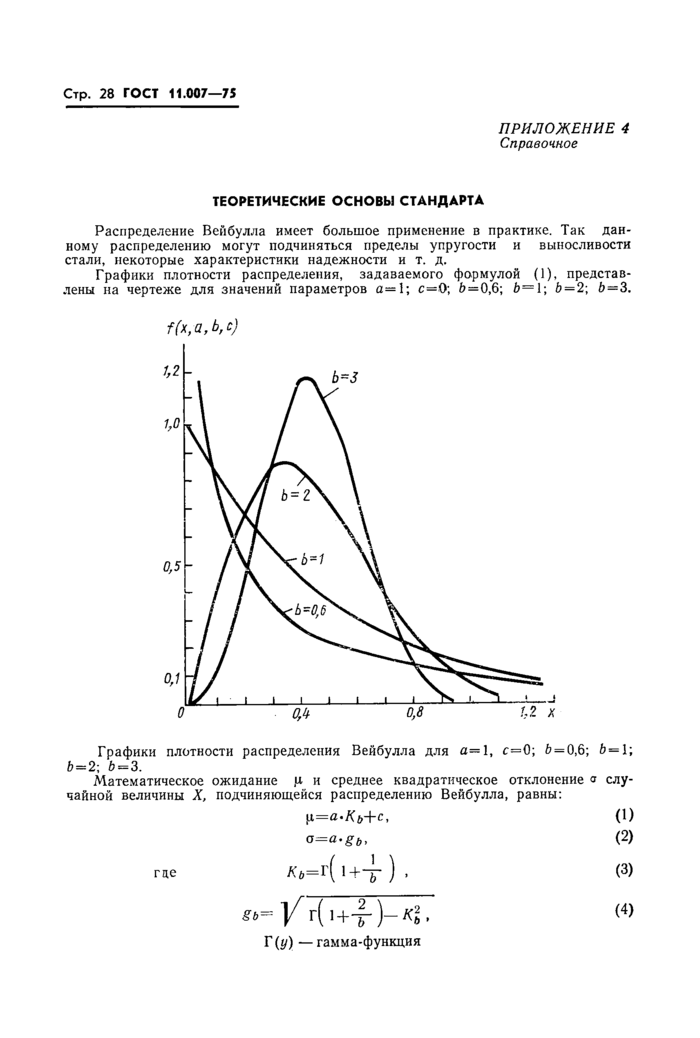
где а — параметр масштаба, b — параметр формы, с — параметр сдвига (см. приложение 4, чертеж).
1.2. Оценка параметров а, Ь, с осуществляется по выборке независимых наблюдений хи х2, . . ., хп случайной величины
X, заведомо подчиняющейся распределению Вейбулла. Согласие наблюдений хи %2> • . хпс распределением Вейбулла — по
гост
11.007-75
Перепечатка воспрещена
Издание официальное
Переиздание. Ноябрь 1977 г.
ГОСТ 11.007-75 Стр. 19
Пример 3. табл. 2 примера 2 дано 100 наблюдений случайной величины X, подчиняющейся распределению Вейбулла. Известно, что 6 =1,2. Методом моментов найти оценки для параметров масштаба и сдвига.
Решение. Из табл. 1 определяют значение коэффициентов К ь и . В нашем случае для 6=1,20 имеем Кь —0,940; g*=0,787.
Определяют среднее значение х и среднее квадратическое отклонение 5
1 юо
|
5= |
(xt*—1,034)2=0,874. |
1*034;
Согласно формуле (7) определяют оценку а для параметра а
- 0,874 ,
0,787 ~1,115*
По формуле (8) определяют
с=1,034—I,115-0,940=— 0,014.
Согласно формуле (9) в качестве оценки параметра сдвига с берут значение с = —0,014, так как
Г=-0,014<*1ОО(1)=0,027.
Таким образом оценки для параметров масштаба а и сдвига с следующие:
а= 1,115; Г=-0,014.
Пример 4. Для 100 наблюдений, приведенных в табл. 2 примера 2, найти методом моментов оценки для параметров масштаба, формы и сдвига распределения Вейбулла.
Решение. Согласно формуле (10) вычисляют:
100
99-98 х*~~ 1 > 034)3
=2,109,
i=\
~ | 100 “|3/2 gg-^(x(.-l,034)2 (=1
где х= 1,034; 5=0,874 получено согласно примеру 2.
По значению р* = 2,109 из табл. 1 находят значение 6 = 0,97; /(* = 1,013; ££ = 1,043. В данном случае применена линейная интерполяция для получения1 значений 6 = 0,97; /(* = 1,013; g*= 1,043.
Согласно п. 5.1 и формуле (7)) вычисляют:
л— 1,043 —°-838-
Стр. 2 ГОСТ 11.007-75
1.3. Стандарт устанавливает правила определения оценок для параметров а, б, с методом моментов для следующих случаев:
[а]—оценка параметра масштаба а при известном значении параметров формы б и сдвига с,
[а, б] —оценка параметров масштаба а и формы б при известном значении параметра сдвига с,
[а, с] —оценка параметров масштаба а и сдвига с при известном значении параметров формы б,
[а, б, с] —оценка всех трех параметров.
Стандарт устанавливает правила определения доверительных границ для параметров а, б, с для случаев:
[а] — определение доверительных границ для параметра а при известных значениях параметров формы б и сдвига с;
[а, б] —определение доверительных границ для параметров масштаба а и формы б при известном значении параметра сдвига с.
2. ОЦЕНКА ПАРАМЕТРА МАСШТАБА а ПРИ ИЗВЕСТНОМ ЗНАЧЕНИИ ПАРАМЕТРОВ ФОРМЫ b И СДВИГА с (СЛУЧАЙ [а]]
2.1. Оценка параметра а при известном значении параметров бис осуществляется по формуле
п \1_
s у
~\ /
(См. приложение 2, пример 1).
3. ОЦЕНКА ПАРАМЕТРОВ МАСШТАБА а И ФОРМЫ b ПРИ ИЗВЕСТНОМ ЗНАЧЕНИИ ПАРАМЕТРА СДВИГА с (СЛУЧАЙ [а, Ь])
3.1. Оценка параметров а и б при значении параметра с осуществляется следующим образом:
вычисляют выборочное среднее арифметическое значение х и выборочное среднее квадратическое отклонение 5 по формулам:
п
*=4*2**> (з)
(4)
(4)
t=\ t=l
ГОСТ 11.007-75 Стр. 3
а также отношение
= , (5)
X—С
по полученному значению vb из табл. 1 находят значение оценки Ь параметров Ь и значение коэффициента Къ\
по полученному значению Кь определяют оценку для параметра а по формуле
(6)
X—с
Кь
Если в табл. 1 нет соответствующего значения vb, то необходимо воспользоваться линейной интерполяцией (см. приложение 2, пример 2).
4. ОЦЕНКА ПАРАМЕТРОВ МАСШТАБА а И СДВИГА с ПРИ ИЗВЕСТНОМ ЗНАЧЕНИИ ПАРАМЕТРА ФОРМЫ Ъ (СЛУЧАИ [ат с])
4.1. Оценка параметров а и с при известном значении параметра b = b0 осуществляется следующим образам:
по значению параметра b = b0 из табл. 1 находят значение коэффициентов gb и Кь ;
определяют оценку для параметра а по формуле
(7)
- S
а=—
ёь
где S — определяется согласно формуле (4); находят значение с по формуле
с х аКь (3)
в качестве оценки параметра с берут одно из двух значений:
(9)
с =
I с, если с<хл(1).
1лгл(1), еслис>л:/г(1), где х„(1)—наименьшее значение среди наблюденных значений
(См. приложение 2, пример 3).
5. ОЦЕНКА ПАРАМЕТРОВ МАСШТАБА а ФОРМЫ Ь И СДВИГА с {СЛУЧАЙ [а Ь.с])
5.1. Оценка параметра а осуществляется следующим образом: определяют асимметрию р4 по формуле
Стр. 4 ГОСТ 11.007-75
(Х(—Х)3
(га—1) (л-2) ^ Р*=Г—-п-~
(10)
"I3/!
по полученному значению р6 из табл. 1 находят оценку Ь параметра b и значения коэффициентов gb и /С*;
по полученному значению b осуществляют оценку параметров. а и с согласно разд. 4.
(См. приложение 2, пример 4).
6. ПРАВИЛА ОПРЕДЕЛЕНИЯ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРА МАСШТАБА а ПРИ ИЗВЕСТНЫХ ЗНАЧЕНИЯХ ПАРАМЕТРОВ ФОРМЫ b И СДВИГА с (СЛУЧАЙ [а])
6.1. Определение доверительных границ для параметра а при известном значении параметров b и с сводится к определению доверительных границ для параметров экспоненциального распределения и осуществляется следующим образом:
из совокупности наблюдений хи х2, . . хп образуют
совокупность величин
Ух={Х —с)Ь> Уг = {Хъ—с)Ь,...,уп={Хп—с)Ь\
по совокупности значений уь уъ> • • •, у п согласно
ГОСТ 11.005-74 образуют доверительные границы для парамет-, 1
pa л = — экспоненциального распределения;
|
1 |
вычисляют нижнюю доверительную границу для параметра а по формуле
|
1 |
гдеХв— верхняя доверительная граница для параметра X, найденная согласно ГОСТ 11.005-74; вычисляют верхнюю доверительную границу для параметра а по формуле
где Ан— нижняя доверительная граница для параметра А, най-денная согласно ГОСТ 11.005-74;
ГОСТ 11.007'—75 Стр. 5
нижняя и верхняя доверительные границы ан, ав образуют доверительный интервал для параметра а, соответствующий доверительной вероятности у*
7*=Ti+T.-l. (13)
Ti>0.5; т2>0Д
где — односторонняя доверительная вероятность, соответствующая доверительной транице ан;
72 — односторонняя доверительная вероятность, соответствующая верхней доверительной границе ав.
Вер {л>лн) = т1; Вер {а\<ав}=т2.
(См. приложение 2, пример 5).
7. ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ МАСШТАБА а И ФОРМЫ b ПРИ ИЗВЕСТНОМ ЗНАЧЕНИИ ПАРАМЕТРА СДВИГА с (СЛУЧАЙ [а, Ъ]).
7.1. Определение нижней доверительной границы b н для параметра b при неизвестном значении параметра а и известном значении параметра с осуществляется следующим образом: задают одностороннюю доверительную вероятность Уь
вычисляют корень Ь уравнения (1) приложения 1; по заданному объему выборки п (5</г<120) и заданному значению Vi в табл. 2 находят значение коэффициента /н;
вычисляют нижнюю доверительную границу для параметра Ь по формуле
при значении объема выборки /г> 120 значение коэффициента /н вычисляют по формуле
, 1 , 1 / 0,608
^н=1+ у (15)
где иУх — квантиль нормального распределения, соответствующая вероятности Yi (см. табл. 4).
7.2. Определение верхней доверительной границы Ьв для параметра b при неизвестном значении параметра а и известном значении параметра с осуществляется следующим образом: задают одностороннюю доверительную вероятность Уг;
вычисляют корень b уравнения (1) приложения 1; по заданному объему выборки п (5<п<120) и значению из табл. 2 находят значение коэффициента 1В\
Стр. 6 ГОСТ 11.007-75
вычисляют верхнюю доверительную границу для параметра Ь по формуле
б.-f ; (16)
LB
при значении объема выборки «>120 значение /в определяется по формуле
, , _ /0.608
г /г * ^V2 - (17)
где значение иУг —приведено в табл. 4 (см. п. 7.1). (См. приложение 2, примеры 6,7).
7.3. Определение доверительного интервала для параметра b при неизвестном значении параметра а и известном значении параметра с осуществляется следующим образом:
задают доверительную вероятность Y* и односторонние доверительные вероятности Yi и у2 таким образом, чтобы у*, yi и У% удовлетворяли соотношению (13);
для односторонней доверительной вероятности у \ согласно п. 7.1 определяют нижнюю доверительную границу Ьп\
для односторонней доверительной вероятности у2 согласно п. 7.2 определяют верхнюю доверительную границу Ьв;
нижняя Ьн и верхняя Ьв доверительной границы образуют доверительный интервал для параметра b с доверительной вероятностью
Т * = Т1+Т 2— 1 •
(См. приложение 2, примеры 6,7).
7.4. Определение нижней доверительной границы ан для параметра а при неизвестном значении параметра Ъ и известном значении с осуществляется следующим образом:
задают одностороннюю доверительную вероятность Уь
вычисляют корни b я а уравнений (1), (2) приложения 1; по заданному объему выборки « (5<«<120) и значению yt из табл. 3 находят значение коэффициента гн;
вычисляют нижнюю доверительную границу для параметра а по формуле
л
Л ~ZJb * V
а^а-е ; (18)
при значении объема выборки «>120 значение гн вычисляют по формуле
(19)
/1 108" п ’
где значение иУх —приведено в табл. 4 (см. п. 7.1).
ГОСТ 11.007-75 Стр. 7
|
Таблица 1 Значения Кь* г 8Ь> » v Ы Рг>» ?о для заданных значений b | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Продолжение табл. 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Таблица 2 Значения / н и / в | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|