ГОСТ 11.005-74
Прикладная статистика. Правила определения оценок и доверительных границ для параметров экспоненциального распределения и распределения Пуассона
Купить ГОСТ 11.005-74 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Устанавливает правила определения оценок и доверительных границ для параметров экспоненциального распределения и распределения Пуассона по совокупности статистических опытных данных, полученных на производстве в процессе измерений, испытаний и анализов, если эти опытные данные подчиняются экспоненциальному распределению или распределению Пуассона.
Стандарт содержит два справочных приложения, в которых даны примеры применения правил стандарта, общие понятия и обозначения, а также кратко изложены теоретические основы стандарта.
Переиздание. Апрель 1984 г.
Отменен без замены.
Оглавление
1. Общие положения
2. Определение оценок параметров экспоненциального распределения
3. Определение доверительных границ для параметров экспоненциального распределения
4. Распределение Пуассона
Приложение 1 (справочное) Примеры применения правил стандарта
Приложение 2 (справочное) Общие понятия и обозначения. Теоретические основы стандарта
Литература
| Дата введения | 01.01.1975 |
|---|---|
| Добавлен в базу | 01.01.2019 |
| Завершение срока действия | 01.03.1987 |
| Актуализация | 01.01.2021 |
Организации:
| 08.07.1974 | Утвержден | Государственный комитет стандартов Совета Министров СССР | 1641 |
|---|---|---|---|
| Издан | Издательство стандартов | 1985 г. |
Applied statistics. Estimation of values and confidence intervals for exponential distribution and Poisson distribution parameters
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12
стр. 13
стр. 14
стр. 15
стр. 16
стр. 17
стр. 18

стр. 19

стр. 20

стр. 21

стр. 22

стр. 23
стр. 24

стр. 25

стр. 26
стр. 27

стр. 28

стр. 29

стр. 30
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРИКЛАДНАЯ СТАТИСТИКА
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ И РАСПРЕДЕЛЕНИЯ ПУАССОНА
ГОСТ 11.005—74
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ Москва
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
Прикладная статистика
ГОСТ П.005—74
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ И РАСПРЕДЕЛЕНИЯ ПУАССОНА
Applied statistics. Estimation of values and confidence intervals for exponential distribution and Poisson distribution parameters
Постановлением Государственного комитета стандартов Совета Министров СССР от 8 июля 1974 г. № 1641 срок введения установлен
с ,01.01.75
Настоящий стандарт устанавливает правила определения оценок и доверительных границ для параметров экспоненциального распределения и распределения Пуассона по совокупности статистических опытных данных, полученных на производстве в процессе измерений, испытаний и анализов, если эти опытные данные подчиняются экспоненциальному распределению или распределению Пуассона.
Стандарт содержит два справочных приложения, в которых даны примеры применения правил стандарта, общие понятия и обозначения, а также кратко изложены теоретические основы стандарта.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Правила определения оценок и доверительных границ для параметров экспоненциального распределения изложены в настоящем стандарте для двух случаев:
а) полностью определенная выборка объема п, т. е. такая выборка, в которой все значения хи хъ..., хп случайной величины х определены;
б) неполностью определенная выборка объема п, т. е. такая выборка, в которой известны только т значений случайной величины х(т<п): хь ..., хт, а про остальные п—т значений известно только, что эти значения больше некоторого числа хи.
Издание официальное *
Правила определения оценок и доверительных границ для параметра распределения Пуассона изложены для случая полностью определенной выборки.
Перепечатка воспрещена
Переиздание. Апрель 1984 г.
© Издательство стандартов, 1985
|
Продолжение табл. 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
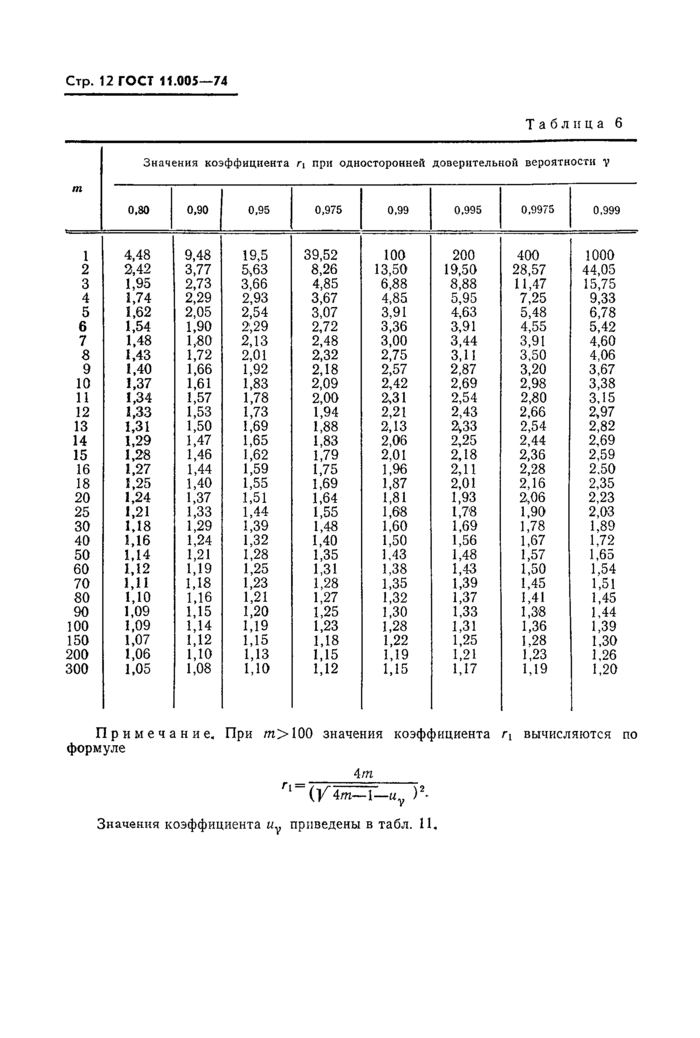
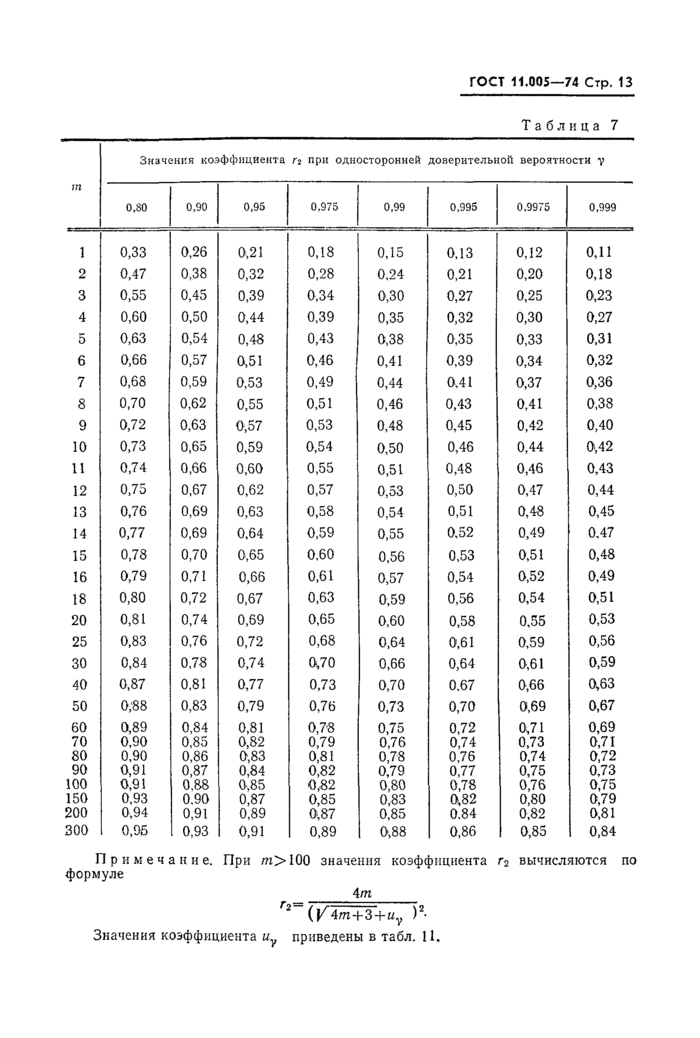
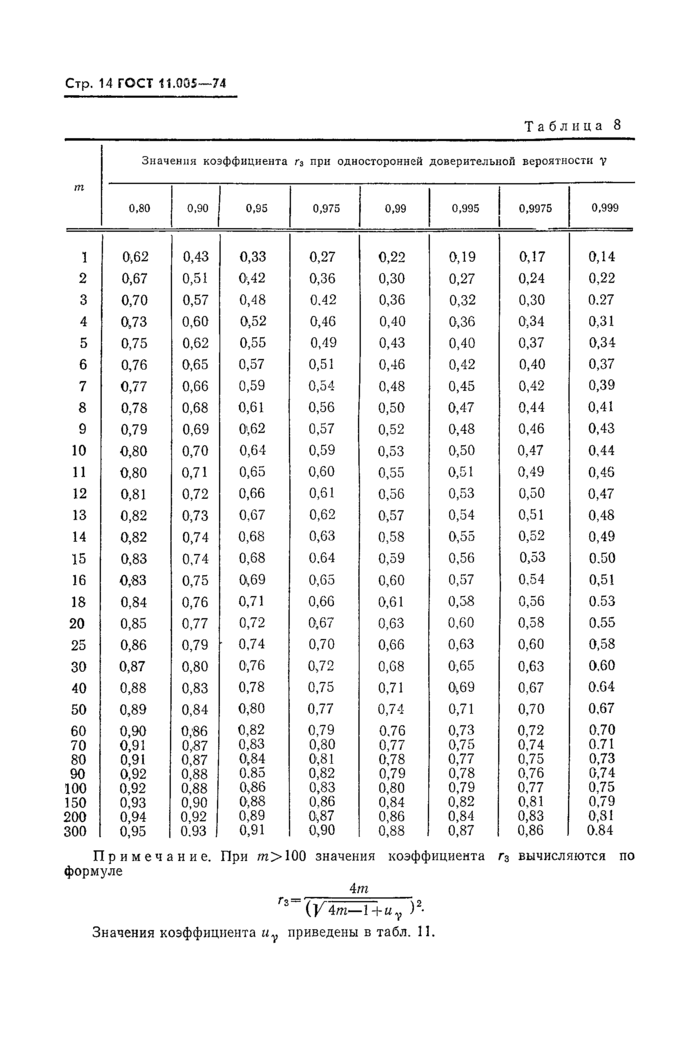
Примечание. Оценка X определяется по соответствующей строке табл. 3, коэффициенты г и г2, Гз> г4, г5, г0 определяются из табл. 6, 7, 8, 9, 10, 11 по у и пг или п, остальные обозначения — см. табл. 1.
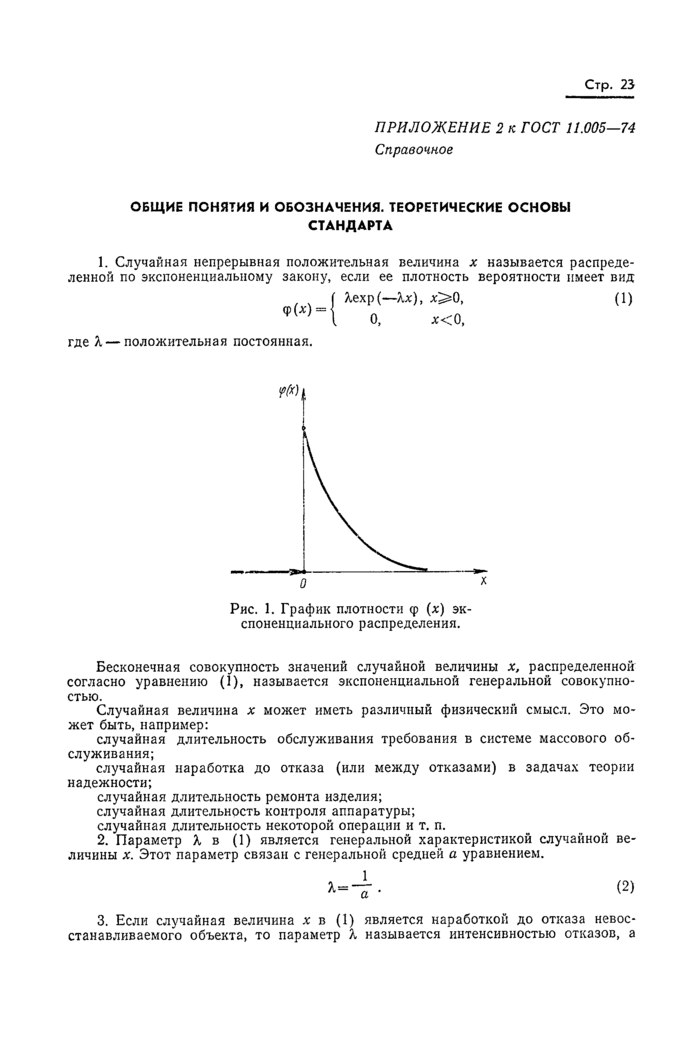
4. РАСПРЕДЕЛЕНИЕ ПУАССОНА
4.1. Распределение Пуассона имеет один параметр а, который равен математическому ожиданию случайной величины. Оценка этого параметра дается формулой
a~k, (10)
где k — наблюденное значение случайной величины.
ГОСТ 11.005-74 Стр. И
|
k "Г“ J г 1 |
(п) |
|
k d в=— , Г 2 |
(12) |
|
при & = 0 | |
|
й и II о |
(13) |
|
й и II о |
(14) |
|
Коэффициенты гъ г2 находятся из табл. 6 и 7 по |
заданному |
Y и m = k\ коэффициент г0 находится из табл. 11.
4.3. Если из партии изделий объема N берется выборка объема п, то случайное число k дефектных изделий в выборке имеет распределение Пуассона при выполнении следующих двух условий:
n<0y\N,
доля q дефектных изделий в партии не превосходит 0,1.
При выполнении этих условий параметр а распределения Пуассона находится по формуле
4.2. Нижняя и верхняя доверительные границы для параметра а (соответственно (ан и ав) находятся по следующим формулам: при /гфО
a = nq. (15)
4.4. Если выполняются условия, указанные в п. 4.3, и в выборке объема п обнаружено k дефектных изделий, то оценка доли q дефектных изделий в партии находится по формуле
?--• (is»
?н=—.
(17)
(18)
(19)
(?Н=0,
(20)
|
?н=—. |
(17) |
|
(18) | |
|
(19) | |
|
(?Н=0, |
(20) |
Доверительные границы для q при k^O находят по формулам
Если й = 0, то
|
Значения коэффициента п при односторонней доверительной вероятности v | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Примечание, При т> 100 значения коэффициента гх вычисляются по формуле
4 т
г^(ущ=Т-иу у.
Значения коэффициента иу приведены в табл. 11,
|
Значения коэффициента г2 при односторонней доверительной вероятности v | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
по |
Примечание. При т>100 значения коэффициента г2 вычисляются формуле
_4т_
Гг ()^4т+3+ц? )2* Значения коэффициента иу приведены в табл. 11,
|
Значения коэффициента г3 при односторонней доверительной вероятности v | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
_4т_
Примечание. При щ>100 значения коэффициента г3 вычисляются по формуле
Гз {V 4т— 1+иу )2* Значения коэффициента иу приведены в табл. 11.
ГОСТ 11.005-74 Стр. 15
|
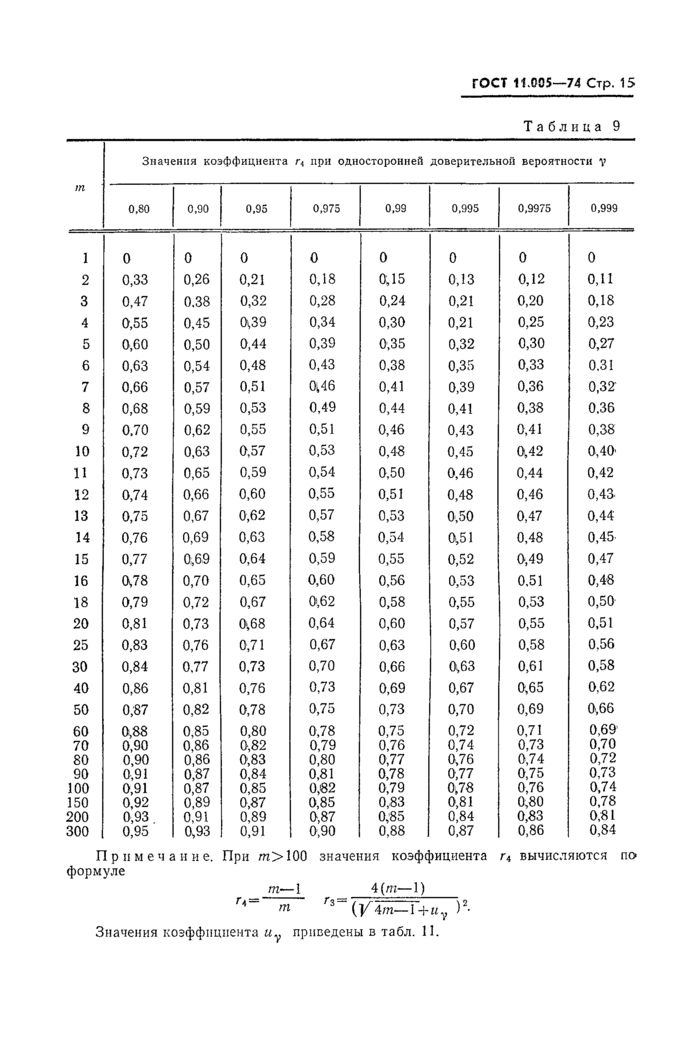
Таблица 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
т—1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание. При т>100 значения коэффициента г4 вычисляются па формуле
г3 =
4 (т—1)
т ' ° ’7 ' ’ ■ ‘2
Значения коэффициента приведены в табл. 11.
|
Таблица 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание. При ш>100 значения коэффициента г5 вычисляются по формуле
т—1 4 (т— 1)
Г5= т Г‘= (УШ^Л—и v )2
Значения коэффициента ttv приведены в табл. 11.
ГОСТ 11.005-74 Стр. 17
|
Таблица 11 Значения коэффициентов г0 н и | |||||||||||||||||||||||||||
|
ПРИЛОЖЕНИЕ 1 к ГОСТ 11.005-74 Справочное
ПРИМЕРЫ ПРИМЕНЕНИЯ ПРАВИЛ СТАНДАРТА
В приводимых примерах применимость экспоненциального распределения (в пп. 1—5) или распределения Пуассона (в п. б) предполагается заранее известной.
1. Примеры для случая полностью определенной выборки
Пример 1. На опыте получено три значения продолжительности ремонта» 350, 400 и 510 ч. Найти оценку и доверительные границы для средней продолжительности ремонта при доверительной вероятности 0,90.
Решение. Здесь п—3, у=0,90, выборка полностью определенная. Согласно подпункту 1 табл. 2 настоящего стандарта находим
Т=4г (350+400+510) =420 ч.
Доверительные границы находим по подпункту 1 табл. 4 настоящего стандарта. Из табл. 6 и 7 настоящего стандарта для т~3 и у—0^90 определяем т 1 — 2,73, г3=0,57. Далее находим ан = 0,57*420=240 ч; ав —2,73*420= 1147 ч.
Пример 2. В условиях примера 1 найти оценку и доверительные границы для %.
Решение. Согласно подпункту 1 табл. 3 настоящего стандарта находим
2 1 350+400+510 =0’0016 ч •
Доверительные границы находим по подпункту 1 табл. 5 настоящего стандарта. Из табл. 9 и 10 для пг = 3 и у = 0,90 определяем 7*4 = 0,38* г5=1,82, Далее находим
_ 0,0016 1,82 0,0016 Хв= 0,38
0,00088--- ; 0,0043 — .
2. Примеры для планов испытаний [AT, R, 7], [Л/, М, 7], [iV, М, Т £ ]
Пример 3. При испытаниях невосстанавливаемых объектов — электроосветительных ламп — по плану [ЛГ, R, 7] было получено 10' отказов. На испытания было поставлено N=20 ламп, длительность испытаний составляла 7=1000 ч. Найти оценку и доверительные границы для средней наработки до отказа при доверительной вероятности 0,80.
Решени е. Воспользуемся уравнениями в подпунктах 2 табл. 2 и 4 настоящего стандарта. Из табл. 6 и 7 настоящего стандарта для /п=10 и у — 0,80 находим
rj = 1,37, /*2=0,73. Далее имеем
х=
20*1000
10
=2000
ч;
ав== 1,37-2000 = 2740 ч.
Пример 4. В условиях примера 3 найти оценку и доверительные границы .для интенсивности отказов.
Решение. Воспользуемся уравнениями в подпунктах 2 табл. 3 и 5 настоящего стандарта и данными примера 3. Получаем
|
Л |
10 |
=0,5-Ю-3 |
|
А — |
20-1000 | |
|
0,5-10-3 |
. 1 | |
|
Ян — |
1,37 |
=0,36-ю-3 — ; |
|
0,5-10-3 |
. 1 | |
|
Яв = |
0,73 |
=0,68-10-3 — . |
Пример 5. При испытаниях холодильников по плану [JV, Mf 7] не было получено отказов. При этом было Af=10, 7=1000 ч. Найти доверительные границы для наработки на отказ и параметра потока отказов при доверительной вероятности 0,05.
Решение. Воспользуемся выражениями в подпункте 2 табл. 4 и 5 настоящего стандарта. По табл. 11 настоящего стандарта для находим
Го = 3,00.
Далее имеем
ю.1000
ан =-з-=3333 ч;
ав = оо;
Яв =
—3__з.ю-4 1.
10-1000 ~а 1и ч ’
Ян — 0.
3. Примеры для плана испытаний [ЛГ, £/, 7]
Пример 6. При испытаниях полупроводниковых приборов по плану [N, U, 7] было получено пять отказов. При этом было А^ = 20, 7 = 600 ч, а наработки до отказа составили ^ = 40 ч, х2 = 60 ч, х3=90 ч, х4 = 210 ч, х5 = 600 ч.
Найти оценку и доверительные границы для средней наработки до отказа при у = 0,80.
Решение. По выражению из подпункта 3 и табл. 2 настоящего стандарта находим
— 40+60+90+210 + 600+15.600 10000
х =-g- =—g— = 2000 ч.
Воспользуемся теперь указаниями п. 3.2 настоящего стандарта.
5
Для у=0,80 и т=5 из табл. 6 и 7 настоящего стандарта определяем П = 1,62, г2=0,63. Далее по формулам (6) и (7) настоящего стандарта вычисляем
5
Стр. 2 ГОСТ 11.005-74
1.2. Определение оценок и доверительных границ для экспоненциального распределения на практике чаще всего проводится для расчета характеристик надежности по результатам специально организованных испытаний или наблюдений.
В табл. 1 приведены характеристики двенадцати наиболее часто применяемых планов испытаний на надежность. Их можно разделить на три группы:
планы с индексом R, т. е. планы испытаний невосстанавлива-емых объектов, согласно которым отказавшие во время испытаний объекты заменяются новыми;
планы с индексом U, т. е. планы испытаний невосстанавлива-емых объектов, согласно которым отказавшие во время испытаний объекты не заменяются новыми;
планы с индексом М, т. е. планы испытаний восстанавливаемых объектов, согласно которым после каждого отказа работоспособность объекта восстанавливается.
1.3. При испытаниях невосстанавливаемых объектов по плану [N, U, г] при r=N получается полностью определенная выборка значений х\. При остальных планах испытаний невосстанавливаемых объектов, приведенных в табл. 1, получаются, как правило, неполностью определенные выборки.
При испытаниях восстанавливаемых объектов по плану [N, М, г] при любом г получается полностью определенная выборка. При остальных планах испытаний восстанавливаемых объектов, приведенных в табл. 1, получаются, как правило, неполностью определенные выборки.
1.4. Планы испытаний [N, U, (г, Т)], [Л/, М, (г, Т)]„
[N, R, (У, Т)], [Af, М, )] в дальнейшем называются двойс
твенными, в отличие от остальных планов в табл. 1, которые называются простыми.
При окончании испытаний по каждому двойственному плану получается результат, который соответствует одному из двух простых планов, кроме плана [N, М, (г, Т)]. Так, например, если при испытаниях по плану [N, U, (г, 71)] раньше получается г отказов, чем достигается время Т, то двойственный план (W, U, (г, Т)\ приводит к тому же результату, что и простой план [W, U, г].
1.5. Планы испытаний, приведенные в табл. 1, могут применяться не только для испытаний на надежность; эти планы применимы и в тех случаях, когда случайная величина х имеет физический смысл, не связанный с надежностью.
Стр. 20
Далее по формулам (4) и (5) настоящего стандарта находим
*'в= 1— 20-0,67 ~= 0,627;
|
/,в = 1— 20-1,57 =0,84L Теперь из выражений в подпункте 3 табл. 4 настоящего стандарта находим5 | ||||||||||||
|
Пример 7. В условиях примера 6 найти оценку и доверительные границы* для интенсивности отказов.
Решение. Используя выражения в подпункте 3 табл. 3 и 5 настоящего' стандарта и результаты, полученные в примере 6, получим
|
%— |
5 л 1- п л л о |
1 |
|
10000“ 0,50-0 |
Ч | |
|
0,172 |
1 | |
|
600 =°.29-К»"3 |
Ч | |
|
О 4^ О |
1 | |
|
Ав = |
'боо-=0,78-1°-3 |
Ч |
4. Примеры для планов испытаний R, г], [Л;, U, г], [АА М, г], [N, Mt rz ]
Пример 8. При испытаниях невосстанавливаемых объектов (кинескопов) по плану [N, R, г], где N—20, г—5, последний отказ был получен при длительности испытаний хг = 600 ч.
Найти оценку и доверительные границы для средней наработки до отказа при доверительной вероятности 0,8.
20*600
5
— 2400 ч.
х
Решение. По выражению в подпункте 4 табл. 2 настоящего стандарта находим
Доверительные границы находим по выражениям в подпункте 4 табл. 4 настоящего стандарта. Из табл. 6 и 8 настоящего стандарта по у=0,80 и т = Ъ определяем ri= 1,62, г3=0,75. Далее находим
ан = 0,75*2400— 1800 ч;
ав = 1,62*2400=3890 ч.
(сравните с решением примера 6).
Пример 9. При испытании резисторов по плану [Аг, U, г], где #=20, г=5, отказы были получены при наработках в часах: Xi = 40, х2—60, *3=90, *4=210, *5 = 600.
Найти оценку и доверительные границы для средней наработки до отказа при доверительной вероятности 0,80.
Решение. По выражению из подпункта 4 табл. 2 настоящего стандарта находим
ГОСТ 11.005-74 Стр. 3
|
Таблица 1 Характеристики планов испытаний на надежность | |||||||||||||||||||||
|
Стр. 4 ГОСТ 11.005-74
|
Продолжение табл. 1 | ||||||||
| ||||||||
|
Планы для объектов, восстанавливаемых в процессе испытаний |
|
7 |
[ЛГ, М, Г]; т7^0; s7=nt |
План испытаний, согласно которому испытаниям подлежат N объектов; после каждого отказа работоспособность объекта восстанавливается, каждый объект испытывается до наработки Т |
|
6 |
[N, М, г]; m&—Nr> 0; N S$~ 2 х л £=1 1 |
План испытаний, согласно которому испытаниям подлежат N объектов; после каждого отказа работоспособность объекта восстанавливается, каждый объект испытывается до возникновения у него г отказов |
|
9 |
[IV, М, (г. Г)]; 0^m9^Nr; 0 <S9s£JVr (см. п. 2.2) |
План испытаний, согласно которому испытаниям подлежат N объектов; после каждого отказа работоспособность объекта восстанавливается, каждый объект испытывается либо до возникновения г отказов, либо до наработки Т, в зависимости от того, какое из этих условии будет выполнено раньше |
|
10 |
[N,M,rz ]; miQ—r^ >0; N „ Sio— 2 хfe k— 1 |
План испытаний, согласно которому испытаниям подлежат N объектов; после каждого отказа работоспособность объекта восстанавливается, испытания прекращаются при возникновении суммарного числа rs отказов с учетом всех объектов |
|
11 |
[N,M, Ts ]; mu>0; Sn — T j. |
План испытаний, согласно которому испытаниям подлежат N объектов; после каждого отказа работоспособность объекта восстанавливается, испытания прекращаются при получении Г2 —суммарной наработки всех объектов |
|
12 ■ |
[N,M, (rs Ts )]; mi2=/raI0 или /Пц; Sl2 = Sio ИЛИ 5ц (см. п. 2.2) |
План испытаний, согласно которому испытаниям подлежат N объектов; после каждого отказа работоспособность объекта восстанавливается, испытания прекращаются при возникновении суммарного числа rs отказов с учетом всех объектов или при получении Т%—суммарной наработки всех объектов, в зависимости от того, какое из этих условий будет выполнено раньше |
ГОСТ 11.005-74 Стр. 5
Примечания:
1. В планах 1—6 параметр X экспоненциального распределения называется интенсивностью отказов.
2. В планах 7—12 имеет место простейший поток отказов, параметр которого обычно обозначается через Л. В настоящем стандарте для унификации используется обозначение X вместо Л.
3. Sj — суммарная наработка всех объектов за время испытаний по /-му плану; т\ — суммарное число отказов за время испытаний; xi — наработка г-го объекта до отказа; хг —наработка i-го объекта до r-го отказа; xi —
наработка t-го объекта полностью за время испытаний. В дальнейшем (табл, 2—5) вместо Sj употребляется обозначение S, а вместо т\ — обозначение т.
2. ОПРЕДЕЛЕНИЕ ОЦЕНОК ПАРАМЕТРОВ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
2.1. Экспоненциальное распределение имеет один параметр Х> который связан со средним значением а случайной величины д: соотношением
Оценка среднего значения а случайной величины д: будет обозначаться х; оценка параметра X будет обозначаться X.
Выражения для оценок х приведены в табл. 2.
В случае полностью определенной выборки объема п несмещенная оценка для а определяется по формуле:
x=J_Sxi. (2)
» £-1
При всех планах испытаний, указанных в табл. 1, оценка для а определяется по формуле
где 5 —суммарная наработка всех объектов за время испытаний;
т—суммарное число отказов всех объектов за время испытаний (т> 0).
Оценка по уравнению (3) в одних случаях является смещенной, в других — несмещенной, как указано в табл. 2.
2.2. Можно пользоваться табл. 2 для двойственных планов, Входя в эту таблицу с тем простым планом, к которому привели результаты испытаний по двойственному плану.
В случае плана [W, М, (г, Т)] для приближенного определения. оценок и доверительных границ можно использовать формулу для плана [М М, Т% J.
2.3. Если имеется несколько полностью определенных выборок
любого объема из одной и той же генеральной совокупности, то
несмещенную оценку х можно определить по уравнению (2), объединив все эти выборки в одну общую выборку.
Если имеются результаты нескольких серий испытаний объектов из одной и той же генеральной совокупности по одному и тому же плану, то можно получить общую оценку х по всем этим испытаниям, используя уравнение (3). При этом Sum будут относиться ко всей совокупности результатов испытаний.
2.4. Выражения для оценок К приведены в табл. 3.
Для нахождения оценок Т в случае двойственных планов испытаний, не указанных в табл. 3, используются выражения для соответствующих простых планов, как указано в п. 2.2.
|
Таблица 2 Выражения для оценок х | ||||||||||||||
|
|
ГОСТ 11.005-74 Стр. 7 Продолжение табл. 3 | |||||||||||
| |||||||||||
|
Обозначения см. в табл. 1. |
3. ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРОВ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
3.1. Выражения для аи и аь — соответственно нижней и верхней доверительных границ величины а при односторонней доверительной вероятности у представлены в табл. 4.
При этом следует пользоваться соответствующими оценками из табл. 2 (кроме плана [yV, U, Т]).
Для нахождения доверительных границ в случае двойственных планов испытаний, не указанных в табл. 4, используются выражения для соответствующих простых планов, как указано в п. 2.2.
3.2. Доверительные границы для а в случае плана [N, U, Т] находятся из подпункта 3 табл. 4. В случае т> 0 они выражаются через величины рн, Рв, которые определяются следующим образом:
т
ШГ*
т
(4)
Рн=1
(5)
NR, ’
где Ri, R2 определяются по следующим формулам: в случае
(6)
(7)
в случае
(8)
(9)
Коэффициенты гх и г2 находятся по табл. 6 и 7, в которые надо входить с величинами у и т.
Коэффициенты г\ и г2 находятся по табл. 6 и 7, в которые надо входить с величинами у и m' = N—m.
Если т мало по сравнению с N (т<0,Ш), то приближенно доверительные границы для а в случае плана [Л/, U, Т] можно находить по тем же правилам, что и для плана [N, Rr Т].
3.3. Выражения для Ян и Хв — соответственно нижней и верхней доверительных границ параметра X при односторонней доверительной вероятности у представлены в табл. 5. При этом следует пользоваться соответствующими оценками из табл. 3 (кроме плана [N, U, Т]).
Для нахождения доверительных планов испытаний, не указанных в табл. 5, используются выражения для соответствующих простых планов, как указано в п. 2.2.
Доверительные границы в случае плана [Nf U,T\ находятся с использованием уравнений и указаний п. 3.2 и уравнений
ГОСТ 11.005-74 Стр. 9
|
Таблица 4 Выражения для доверительных границ ап и ав | |||||||||||||||||||||
|
Примечание. Оценка х определяется по соответствующей строке табл. 2, коэффициенты ги г2, г3, г0 определяются из табл. 6, 7, 8 и 11 по у и т или /г, остальные обозначения — см. табл. 1.
|
Таблица 5 Выражения для доверительных границ и %в | |||||||||||||||||||||
|