ГОСТ 21098-82
Цепи кинематические. Методы расчета точности
Купить ГОСТ 21098-82 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Устанавливает методы расчета точности кинематических цепей, состоящих из нерегулируемых зубчатых, червячных и реечных передач винт - гайка, без учета упругих деформаций.
Оглавление
1 Цели и методы расчета точности кинематических цепей
2 Основные расчетные формулы
3 Последовательность расчетов
Приложение 1Термины, применяемые в настоящем стандарте, их обозначения и пояснения
Приложение 2 Расчет погрешности монтажа
Приложение 3 Расчет кинематической точности цепей на ЭЦВМ
Приложение 4 Примеры расчета кинематической погрешности
Приложение 5 Примеры расчета кинематической погрешности и мертвого хода
| Дата введения | 01.01.1984 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Экология
Организации:
| 20.12.1982 | Утвержден | Государственный комитет СССР по стандартам | 4911 |
|---|---|---|---|
| Разработан | Министерство высшего и среднего образования РСФСР | ||
| Издан | Издательство стандартов | 1983 г. |
Cinematik chains. Methods of calculation accuracy
- ГОСТ 10242-81 Основные нормы взаимозаменяемости. Передачи зубчатые реечные. Допуски
- ГОСТ 13506-81 Основные нормы взаимозаменяемости. Передачи зубчатые реечные мелкомодульные. Допуски
- ГОСТ 1643-81 Основные нормы взаимозаменяемости. Передачи зубчатые цилиндрические. Допуски
- ГОСТ 1758-81 Основные нормы взаимозаменяемости. Передачи зубчатые конические и гипоидные. Допуски
- ГОСТ 3675-81 Основные нормы взаимозаменяемости. Передачи червячные цилиндрические. Допуски
- ГОСТ 9178-81 Основные нормы взаимозаменяемости. Передачи зубчатые цилиндрические мелкомодульные. Допуски
- ГОСТ 9368-81 Основные нормы взаимозаменяемости. Передачи зубчатые конические мелкомодульные. Допуски
- ГОСТ 9774-81 Основные нормы взаимозаменяемости. Передачи червячные цилиндрические мелкомодульные. Допуски
- Показать все
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10
стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18
стр. 19

стр. 20

стр. 21

стр. 22

стр. 23
стр. 24
стр. 25

стр. 26

стр. 27

стр. 28

стр. 29

стр. 30
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ЦЕПИ КИНЕМАТИЧЕСКИЕ
МЕТОДЫ РАСЧЕТА ТОЧНОСТИ
ГОСТ 21098-82
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ MocKia
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ЦЕПИ КИНЕМАТИЧЕСКИЕ
МЕТОДЫ РАСЧЕТА ТОЧНОСТИ
ГОСТ 21098-82
1983
1983
Издание официальное
МОСКВА
|
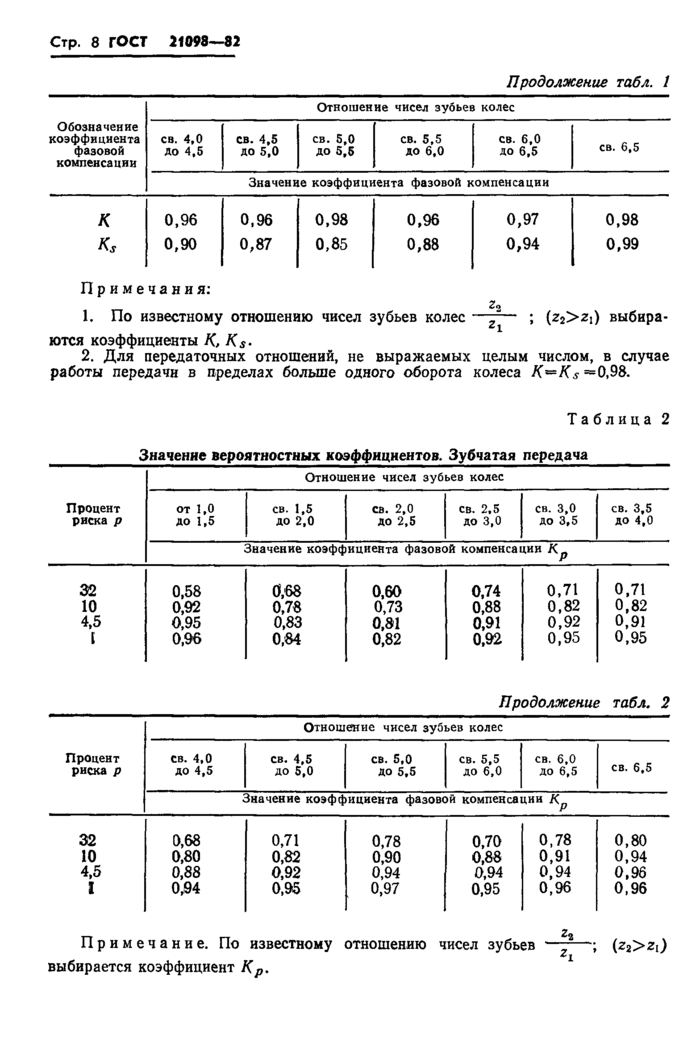
Продолжение табл. 1 | |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
Примечания:
г*
1. По известному отношению чисел зубьев колес —; (z2>z:) выбираются коэффициенты К, Ks-
2. Для передаточных отношений, не выражаемых целым числом, в случае работы передачи в пределах больше одного оборота колеса /С—Кs —0,98.
|
Таблица 2 Значение вероятностных коэффициентов. Зубчатая передача | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Продолжение табл. 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Za
Примечание. По известному отношению чисел зубьев —;—; (z2>Zi)
z1
выбирается коэффициент Кр.
ГОСТ HOW—32 Стр. 9
|
к |
0,90 |
0,95 |
0,80 |
0,80 |
0,95 |
0,95 |
0,88 |
|
К S |
0,07 |
0,17 |
0,40 |
0,65 |
0,65 |
0,60 |
0,59 |
Значение коэффициента фазовой компенсации. Зубчатая реечная передача
|
Таблица 3 | ||||||||||||||||||||||||
| ||||||||||||||||||||||||
|
Продолжение табл. 3 Приведенное передаточное отношение | ||||||||||||||||||||||||
| ||||||||||||||||||||||||
Примечание. По известному приведенному передаточному отношению
7/ ZP
1/Пр ——^—находятся коэффициенты К, К s- Коэффициенты фазовой компенсации, приведенные в ГОСТ 10242-81, следует рассматривать как близкие к вероятностным.
|
Таблица 4 Значение вероятностного коэффициента. Зубчатая реечная передача | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Продолжение табл. 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание. По известному приведенному передаточному отношению
tf гр
ипр=-и проценту риска р выбирается значение коэффициента Кр.
|
Таблица & Значение вероятностных коэффициентов. Червячная передача | ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
ГОСТ 21098-82 Стр. 11
ПРИЛОЖЕНИЕ 1 Рекомендуемое
ТЕРМИНЫ, ПРИМЕНЯЕМЫЕ В НАСТОЯЩЕМ СТАНДАРТЕ,ИХ ОБОЗНАЧЕНИЯ И ПОЯСНЕНИЯ
1. Кинематическая цепь—совокупность звеньев или механизмов, предназначенных для передачи движения.
2. Теоретическая кинематическая цепь — кинематическая цепь, составленная из звеньев с абсолютно точными размерами.
3. Реальная кинематическая цепь — кинематическая цепь, составленная из звеньев, которые имеют отклонения от заданных размеров и форм.
4. Ведущее звено —звено передачи, которое сообщает движение парному звену передачи.
5. Ведомое звено — звено передачи, которому сообщает движение парное звено передачи.
6. Погрешность положения — разность положений ведомого звена реальной и теоретической кинематических цепей для одинаковых положений ведущего звена.
7. Кинематическая погрешность кинематической цепи 6<ps —алгебраическая разность между погрешностями положений ведомого звена кинематической цепи (черт. 1)
|
/—кинематическая погрешность; 2—погрешность положения Черт. 1 |
8. Максимальная кинематическая погрешность кинематической цепи бф2тах~“ наиболыное возможное значение кинематической погрешности кинематической
цепи.
9. Минимальная кинематическая погрешность кинематической цепи бф^тш” наименьшее возможное значение кинематической погрешности кинематической цепи, рассчитанное с учетом возможных компенсаций.
10. Прямой ход — выбранное направление движения звеньев кинематической цепи.
11. Обратный ход — направление движения звеньев кинематической цепи, противоположное прямому ходу.
12. Мертвый ход кинематической цепи j^~~ разность положений ведомого звена для одинаковых положений ведущего звена при прямом и обратном ходах кинематической цепи (черт. 2).
13. Передаточный коэффициент погрешности | — коэффициент влияния, учитывающий изменение кинематической погрешности передачи при приведении ее к выходному звену кинематической цепи.
14. Передаточное отношение кинематической цепи — произведение передаточных отношений передач, составляющих кинематическую цепь.
|
/—погрешность положения при прямом ходе; 5—погрешность положения при обратном ходе; 3—мертвый ход |
Черт. 2
Отклонения, погрешности, допуски
15. Допуск на кинематическую погрешность колеса F{ —по ГОСТ 164а—81, ГОСТ 1758-81, ГОСТ 3675-81, ГОСТ 9178-81, ГОСТ 9368-81, ГОСТ 9774-81.
16. Допуск на кинематическую погрешность зубчатой рейки Fг —по ГОСТ
10242—81, ГОСТ 13506-81.
17. Допуск на погрешность винтовой линии на длине нарезанной частя чер*
вяка fhk —по ГОСТ 9774-81, ГОСТ 3675-81.
18. Допуск на погрешность профиля витка червяка — по ГОСТ 9774-81, ГОСТ 3675-81.
19. Наименьшее смещение исходного контура Е //s"“no ГОСТ 1643-81, ГОСТ 9178-81, ГОСТ 10242-81, ГОСТ 13506-81.
20. Наименьшее отклонение толщины витка червяка по хорде Eg^ —по ГОСТ 9774-81, ГОСТ 3675-81.
21. Наименьшее отклонение средней делительной толщины зуба по хорде Eg,—по ГОСТ 1758-81, ГОСТ 9368-81.
22. Допуск на смещение исходного контура Т и — по ГОСТ 1643-81, ГОСТ 9178—81, ГОСТ 10242-81, ГОСТ 13506-81.
23. Допуск на толщину витка червяка по хорде Т§—по ГОСТ 3675-81* ГОСТ 9774-81.
24. Допуск на среднюю делительную толщину зуба по хорде Т$—по ГОСТ 1758—81, ГОСТ 9368-81.
25. Накопленная погрешность шага резьбы 6fs — разность между действительным и номинальным расстояниями между любыми несоседними профилями витков по образующим среднего диаметра.
26. Предельное отклонение среднего диаметра винта:
верхнее Ъ'\ нижнее Ь" — по ГОСТ 9562-60.
27. Верхнее отклонение среднего диаметра гайки Ь — по ГОСТ 9562-60.
28. Предельные отклонения межосевого расстояния ±fa — по ГОСТ 1643—81, ГОСТ 9178-81, ГОСТ 10242-81, ГОСТ 13506-81.
29. Предельные отклонения межосевого расстояния в передаче ±/а—по ГОСТ 9774-81, ГОСТ 3675-81.
30. Предельные осевые смещения зубчатого венца ±/дм—по ГОСТ 1758—81 ГОСТ 9368-81.
31. Предельные отклонения межосевого угла ±ES — по ГОСТ 1758-81, ГОСТ 9368-81.
3i2. Предельные отклонения межосевого расстояния в обработке ±fac~~ по ГОСТ 3675-81, ГОСТ 9774-81.
33. Гарантированный боковой зазор Jnmin — по ГОСТ 1643-81, ГОСТ 1758—81, ГОСТ 9368-81, ГОСТ 3675-81, ГОСТ 9774-81, ГОСТ 10242-81, ГОСТ 13506-81, ГОСТ 9178-81.
ГОСТ 21098-82 Стр. 13
34. Номинальный межосевой угол в передаче 2—по ГОСТ 16560-70.
35. Угол наклона винтовой линии ф — по ГОСТ 11703-66
36. Поле рассеяния V — по ГОСТ 16319-80.
37. Координата середины поля рассеяния Ev— по ГОСТ 16319-80.
38. Коэффициент риска t — по ГОСТ 16319*—80.
39. Фазовая компенсация — уменьшение кинематической погрешности передачи в зависимости от начального относительного положения звеньев.
40. Коэффициент фазовой компенсации К, Ks —коэффициент, учитываю* щий степень изменения кинематической погрешности от начального положения звеньев.
41. Монтажное радиальное биение зубчатого колеса ег—составляющая радиального биения зубчатого венца колеса, вращающегося на рабочей оси, определяемая радиальным биением поверхности, сопряженной с посадочным местом колеса.
42. Монтажное осевое биение зубчатого колеса еа —составляющая осевого биения зубчатого венца колеса, вращающегося на рабочей оси, определяемая осевым биением поверхности, сопряженной с посадочным местом колеса.
43. Первичные радиальные биения колеса — погрешности, создающие радиальные биения поверхности, сопрягаемой с посадочным местом колеса.
44. Первичные осевые биения колеса — погрешности, создающие осевые биения поверхности, сопрягаемой с посадочным местом колеса.
Стр. 14 ГОСТ 21098-82
ПРИЛОЖЕНИЕ 2 Рекомендуемое
РАСЧЕТ ПОГРЕШНОСТИ МОНТАЖА
1. Колеса зубчатые цилиндрические, конические и червячные
1.1. Показателями точности монтажа зубчатых колес являются:
а) ег — монтажное радиальное биение зубчатого колеса;
б) е а— монтажное осевое биение зубчатого колеса.
1.2. Суммарная приведенная погрешность монтажа вычисляется на основании зависимости
(D
где а — угол исходного профиля колеса;
Р — делительный угол наклона линии зуба, для конических зубчатых колес — к образующей начального конуса.
1.3 В том случае, если не заданы допуски на монтажные радиальные и осевые биения зубчатых колес, их следует принимать равными:
(2)
где е i — допуски на погрешности, создающие первичные радиальные биения
колеса;
е / — допуски на погрешности, создающие первичные осевые биения колеса.
1 4 Допуски на погрешности, создающие первичные радиальные и осевые биения колеса, определяются на основании рабочих чертежей или другой технической документации.
2. Цилиндрические червяки
2 1 Показателями точности монтажа червяка являются радиальное биение витк< и е. и осевое биение еа.
2 2 Суммарная приведенная погрешность монтажа вычисляется на основании зависимости
(3)
тде a t торцовый угол профиля;
I — делительный угол подъема линии витка червяка.
3. Винты
3.1 Показателями точности монтажа винта являются радиальное биение витков ег и осевое биение е ,.
3.2. Суммарная приведенная погрешность монтажа вычисляется на основании зависимости
В2М= V ea+(er tg^)2
(4)
ГОСТ 21098-82 Стр. 15
ПРИЛОЖЕНИЕ Э Рекомендуемое
РАСЧЕТ КИНЕМАТИЧЕСКОЙ ТОЧНОСТИ ЦЕПЕЙ НА ЭЦВМ
1. Рекомендуемый алгоритм расчета кинематической погрешности и мертвого хода согласно черт. 1.
2. Исходные данные для расчета подготавливаются согласно таблице рекомендуемого приложения 5.
3. Алгоритм выводит на печать значения кинематической погрешности и мертвого хода каждой ступени цепи, суммарное значение кинематической погрешности и мертвого хода, рассчитанные по формулам (31<, 33) и (32, 35) соответственно методами максимума — минимума и вероятностным.
4. В том случае, если алгоритм преимущественно используется для определения кинематической точности одних типов передач, он может быть упрощен путем исключения блоков расчета неиспользуемых видов передач.
5. При необходимости алгоритм может быть приращен путем включения блоков расчета дополнительных видов передач.
6. При использовании ЭВМ малой мощности (Электроника 100, ЭКВМ ТЗ—16 и т. п.) рекомендуется вместе с числом передач последовательно вводить исходные данные.
Примечание. Тип передачи:
1 — зубчатая цилиндрическая;
2 — зубчатая коническая;
3 — червячная цилиндрическая;
4 — зубчатая реечная;
5 — винт — гайка.
бф ър I УсрЕр — значения, рассчитанные вероятностным методом.
Стр. 16 ГОСТ 210»—«2
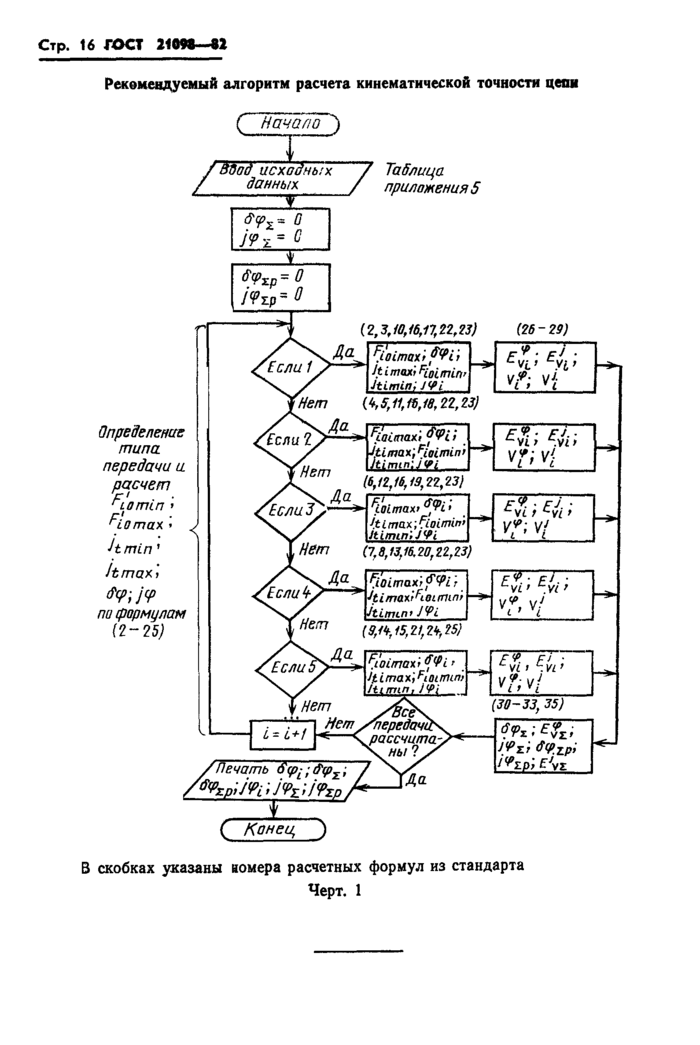
Рекомендуемый алгоритм расчета кинематической точности цепи
С Начало ')
/
Таблица
приложения 5
Определение типа передачи и расчет Fiomln »
г!
r to max »
JtmLn 1 Itmax\ t?<p;jcp па формулам (2~25)
|
Ьдад исходных* данных "Г |
|
/ Печать d'(pL; ; ^zpim'JvTiivTn С Конец ") |
|
(2,3,10,16,1% 22,23) (26-29) | |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
|
Ыа. | |||||||||||||||||||||||||||||||||||
В скобках указаны номера расчетных формул из стандарта
Черт. 1
ГОСТ 21098-82 Стр. 17
ПРИЛОЖЕНИЕ 4 Рекомендуемое
ПРИМЕРЫ РАСЧЕТА КИНЕМАТИЧЕСКОЙ ПОГРЕШНОСТИ
Пример 1
Задача. Рассчитать кинематическую погрешность зубчатой передачи 7—С по ГОСТ 1643-81.
т—3\ 26; z2=90; Е=ES/Vfa =20 мкм; р=10%.
Решение провести методами максимума — минимума и вероятностным. Решение. По ГОСТ 1643-81 и табл. 1 и 2 настоящего стандарта находим значения величин, необходимые для расчета:
Fix —56 мкм; мкм; /С—0,96; Кр —0,82.
Рассчитывается кинематическая погрешность, мкм:
а) метод максимума — минимума (10)
FfOmax - 0.96 (у 56® + 20* + У76* + 20*) = 132,5 ;
б) вероятностный метод (34)
Fl0p~ 0,82-0,96 (J/56* + 20* + ]/76a + 20»)= 113,2.
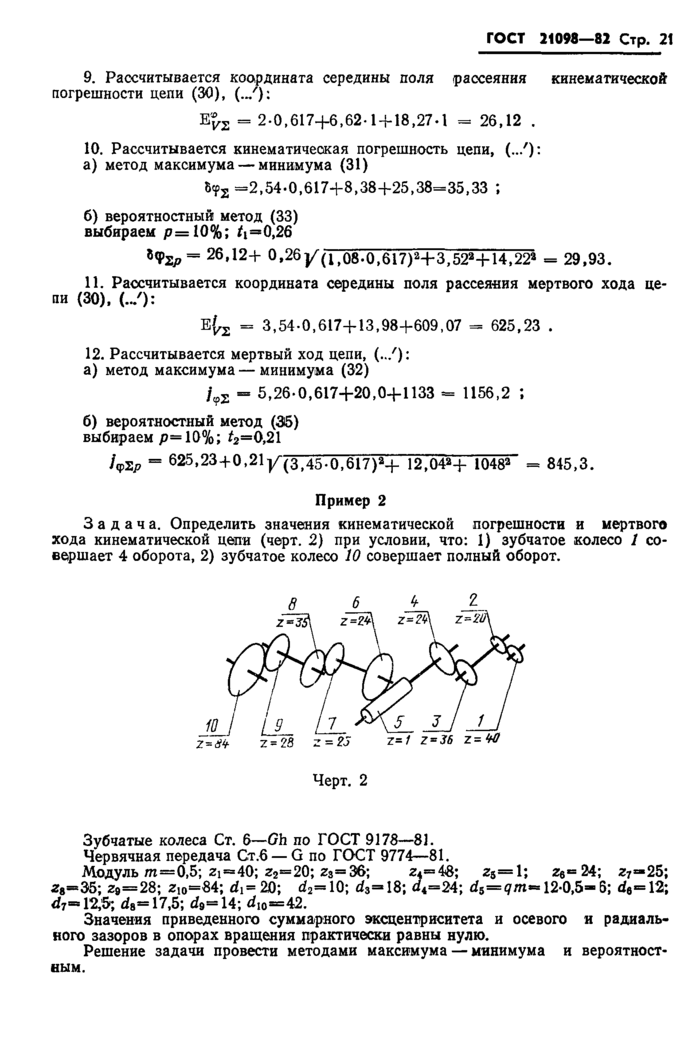
Пример 2
Задача. Рассчитать кинематическую погрешность зубчатой реечной передачи.
Зубчатое колесо 6—С по ГОСТ 1643-81: гК“20; мкм.
Зубчатая рейка 6—G по ГОСТ 10242—^81: гр —28; т=3; р«4^5%.
Решение провести методами максиму ма — минимума и вероятностным. Решение. По ГОСТ 1643-81, ГОСТ 10242-81 и табл. 3 и 4 настоящего стандарта находим значения величин, необходимые для расчета:
E 'i= 40 мкм; Fi% «52 мкм; Я**0,95; К р «0,88.
Рассчитывается кинематическая погрешность, мкм:
а) метод максимума—минимума (13)
F'iOmax = °.95 (]/402 + 20* + 52) == 92;
б) вероятностный метод (34)
F'i0р« 0,88-92«85.
Пример 3
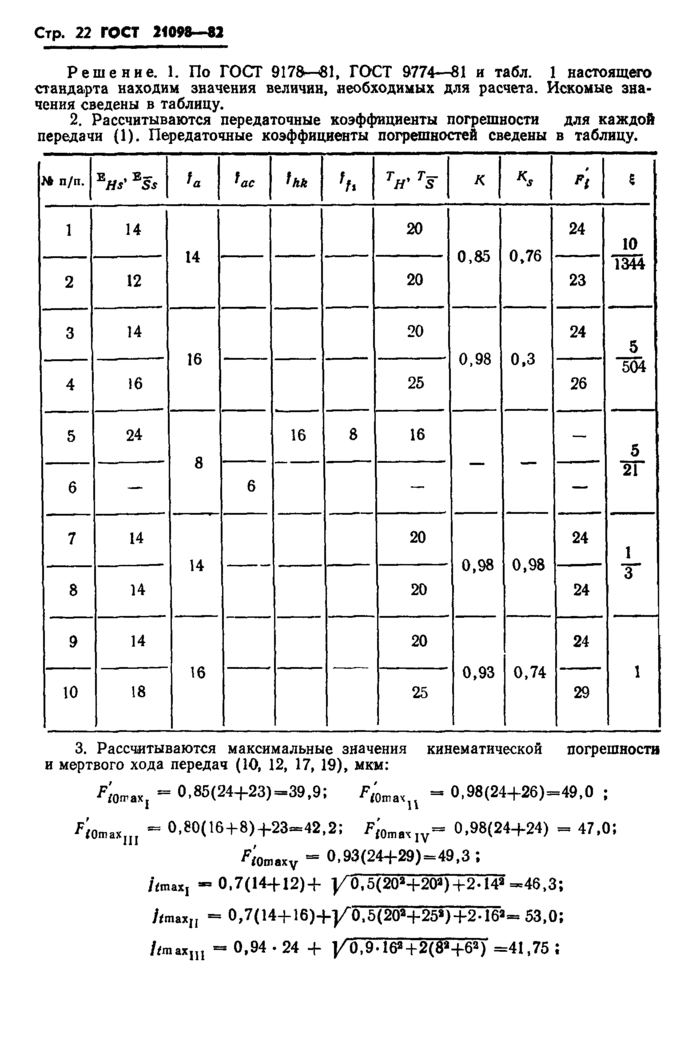
_ 3 а ^?^5Сч^1'ать кинематическую погрешность червячной передачи СТ-о по ГОСТ 3675-81:
т= 2; 2к —80; 2Ч«1; еГг ~еQi =15 мкм; а«20°; у«20°; ESiWi=21,5 мкм; р™ —4,5%.
Решение провести методами максимума — минимума и вероятностным. Решение. По ГОСТ 3675-81 находим значения величин, необходимые для расчета: ^«14 мкм; /^=7,1 мкм; F/a*=23 мкм; /Ср=0,89;
ESAit “ 1>2 УТ& + (15tg20° tg20°)a «18,2 мкм .
РАЗРАБОТАН Министерством высшего и среднего специального образования РСФСР
ИСПОЛНИТЕЛИ
В. А. Вышло*, канд. техн. наук (руководитель темы); С- С. Воронов, канд. техн. наук; Л. В. Гусакова
ВНЕСЕН Министерством высшего и среднего специального образования РСФСР
Зам. министра Э. К. Калинин
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 20 декабря 1982 г. № 4911
© Издательство стандартов, 1983
Стр. 18 ГОСТ 21093-82
Рассчитывается кинематическая погрешность, мкм:
а) метод максимума — минимума (12)
Fornax -0.8]Л 14 +7,1)4-18,* + )/23а + 21,5* = 53,77 ;
б) вероятностный метод (34)
F'lOp - 0,89*53,77 = 47,86.
Пример 4
Задача. Рассчитывать кинематическую погрешность передачи винт—гай* ка; —50 мкм; Еш—30 мкм; р=4,5%; /(р—0,86.
Решение провести методами максимума — минимума и вероятностным.
Решение
Рассчитывается кинематическая погрешность, мкм:
а) метод максимума — минимума (14)
F'i0wsx - /502 + 30* = 58,26 ;
б) вероятностный метод (34)
F't0p = 0,86-58,26 = 50,1 .
УДК 6Ы31.3.001.24(083.74) Группа Г02
ГОСТ
21098—82
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ЦЕПИ КИНЕМАТИЧЕСКИЕ Методы расчета точности
Cinematik chains. Methods of calculation accuraci
Постановлением Государственного комитета СССР по стандартам от 20 декабря 1982 г. Ms 4911 срок введения установлен
с 01.01. 84
Несоблюдение стандарта преследуется по закону
Настоящий стандарт устанавливает методы расчета точности кинематических цепей, состоящих из нерегулируемых зубчатых, червячных и реечных передач и передачи винт — гайка, без учета упругих деформаций.
1. ЦЕЛИ И МЕТОДЫ РАСЧЕТА ТОЧНОСТИ КИНЕМАТИЧЕСКИХ ЦЕПЕЙ
1.1. Устанавливаемые настоящим стандартом методы расчета предназначены для проведения анализа точности кинематических цепей с использованием вероятностного метода и метода максимума — минимума.
1.2. Анализ точности имеет своей целью определение значений показателей точности кинематических цепей, исходя из известных значений показателей точности составляющих звеньев.
1.3. Анализ точности кинематических цепей может проводиться на ЭВМ по алгоритму, приведенному в приложении 3.
1.4. При расчете точности кинематических цепей следует применять:
метод расчета на максимум — минимум, учитывающий только предельное отклонение звеньев кинематической цепи и самые неблагоприятные их сочетания;
вероятностный метод расчета, учитывающий рассеяние погрешностей и вероятность различных сочетаний отклонений составляющих звеньев кинематической цепи.
Стр. 2 ГОСТ 21098-82
1.5- При проведении анализа точности кинематических цепей вероятностным методом процент риска должен выбираться из соображений экономической целесообразности с учетом технических требований к кинематическим цепям. При расчете практически предельного значения кинематической погрешности и мертвого хода процент риска равен 0,27%.
2. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
2.1. Передаточный коэффициент погрешности передач
О)
П ii
ITTf ’
/ 7
где Zj —число зубьев ведущих зубчатых колес или число заходов червяка;
Zj — число зубьев ведомых зубчатых (червячных) колес.
Примечания:
1. Формула (1) справедлива для расчета передаточных коэффициентов передач при задании погрешностей звеньев в угловых единицах.
2. Термины, применяемые в настоящем стандарте, и их пояснения приведены в рекомендуемом приложении 1.
2.2. Минимальное значение кинематической погрешности передач, мкм.
(2)
(3)
1758—81 и ГОСТ
(4)
Передачи зубчатые цилиндрические по ГОСТ 1643-81 и ГОСТ 9178-81
гаш.-отлр’,,+гу
для степеней точности 7,8
F-h)
Передачи зубчатые конические по ГОСТ 9368-81
Р\.)
(5) 1 и
(6) >СТ
(7)
(5) 1 и
(6) >СТ
(7)
для степеней точности 7,8
^omin ~ 0,72Кs (77[1 + ^г,)
Передачи червячные цилиндрические по ГОСТ 3675—81 и
Передачи зубчатые реечные по ГОСТ 10242—81 и ГОСТ
13506—81
^ош.п = адо,7(/А, + /ь) + г;11
ГОСТ 21098—$2 Стр. 3
для степеней точности 7,8
- 0.71 <n + f;.> (8)
Передача винт—гайка
f;«,»-0.62«2 (9)
Примечание. Значения коэффициентов фазовой компенсации К а выбираются из табл. 1 или 3 в зависимости от вида передач.
2.3. Максимальное значение кинематической погрешности передач, мкм.
Передачи зубчатые цилиндрические по ГОСТ 1643-81 и ГОСТ 9178-81
'•«—-к I У(0' + Ч«. + + Ek,] <10>
Передачи зубчатые конические по ГОСТ 1758-81 и ГОСТ 9368-81
,г;.™-*[v + 4м,+/] on
Передачи червячные цилиндрические по ГОСТ 3675-81 и ГОСТ 9774-81
^„-».8р' (/«+//.)*+ Чм. +/(^)’+ Ч». (12)
(13)
Передачи зубчатые реечные по ГОСТ 10242-81 и ГОСТ 13506-81
Передачи винт — гайка
(14)
Примечания:
1. Значения коэффициентов фазовой компенсации К выбираются из табл. 1 и 3 в зависимости от видов передач.
жением 2.
2. Значения Е ш рассчитываются в соответствии с рекомендуемым прило
2.4. Минимальное значение мертвого хода передач, мкм. Передача винт—гайка
1тт=ь"Ч$ (15)
Остальные виды передач
//min = cosTcosp (1б)
2.5. Максимальное значение мертвого хода передач, мкм. Передачи зубчатые цилиндрические по ГОСТ 1643-81 и
Лшах—0,7(E№l+E№l) +|/л0,5(7^1+ Т^) +2/| + 0^+0^ ^
Передачи зубчатые конические по ГОСТ 1758-81 и ГОСТ 9368-81
/<шахв 0,94(E§St +EsSf)+]/’0,46j[/yWli sin SiP-H/^.sinSJ* +
+ (G2iSin8j*+(G2jSin8s)*+^+(G2 cosSj«—(^oS8t)»} +
Щ + ц )
о*
(18)
Передачи червячные цилиндрические по ГОСТ 3675-81 и ГОСТ 9774-81
it o,ax=0,94E5.s + j/0,9(7* +0*tT+Ж+71Л+ G*,+
+ 0*
09)
Передачи зубчатые реечные по ГОСТ 10242—81 и ГОСТ
13506—81
//max = 0,7 (EHSt + EWs,) + ]/"0,5(7^i+7^i)+2/2 +G^ ^0)
Передача винт — гайка
l*Zmax= + }/■ + 0*, (21)
Примечание. и Gr соответственно осевой и радиальный зазоры в опорах вращения; принимаются равными соответственно осевым и радиальным биениям, рассчитываемым по рекомендуемому приложению 2.
2.6. Значение кинематической погрешности и мертвого хода передач в угловых единицах, (../).
Для зубчатых и червячных передач
6,88F;0
(22)
где d — диаметр делительной окружности ведомого колеса, мм
6,88 jt
h d~
Для передачи винт — гайка
21,6 F
Ю
где РА — ход резьбы, мм
/*“
Р А
21,6 7/
Рк
(23)
(24)
(25)
ГОСТ 21098-82 Стр. 5
2.7. Координата середины поля рассеяния кинематической погрешности и мертвого хода передач, (../).
(26)
(27)
•pi® __ ^фт1п I Ч* ®фтах I .
1 о »
J (pmIn ( Ч" /<рmax f §
где i — порядковый номер передачи.
2.8. Поле рассеяния кинематической погрешности и мертвого хода передач, (../).
— 8?шах I — S?m!n I ? (28)
= /<ртах t — jf rain i . (29)
2.9. Координата середины поля рассеяния кинематической погрешности и мертвого хода кинематической цепи, (../).
|
П | ||||||||||||||
|
| ||||||||||
|
Примечание. Значение кинематической погрешности передачи яри расчете по вероятностному методу |
Г<0Р ~ ах (34)
Значение коэффициента Кр в зависимости от вида передачи и принимаемого процента риска р выбирается из табл. 2, 4, 5, 6
= Ek 4-t, ft )г (35)
Значение коэффициента t2 в зависимости от принимаемого процента риска р выбирается из следующего ряда.
| ||||||||||
|
Примечание. В случае необходимости значения кинематической погрешности и мертвого хода кинематической цепи могут быть приведены к ее входу путем деления полученных значений на передаточное отношение цепи. |
2.11. В том случае, если выходное колесо одной или нескольких передач совершает неполный оборот, соответствующие значения кинематических погрешностей, рассчитанных по формулам (2—8, 10—13), умножаются на коэффициент Ко, значение которого в зависимости от угла поворота выходного колеса <р выбирается из следующего ряда.
| ||||||||||||||
|
Продолжение |
| ||||||||||||||
|
3. ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТОВ |
Последовательность расчетов точности кинематических цепей вероятностным методом и методом максимума — минимума приведена ниже (в скобках указаны номера формул).
3.1. По соответствующей нормативно-технической документации и рабочим чертежам устанавливаются значения величин, необходимые для расчета кинематической погрешности и мертвого хода.
ГОСТ 21098-82 Стр. 7
3.2. Рассчитываются значения передаточных коэффициентов
(1).
3.3. Расчет кинематической погрешности
3.3.1. Рассчитываются максимальные и минимальные значения кинематической погрешности передач, составляющих кинематическую цепь (2—14).
3.3.2. Максимальные и минимальные значения кинематических погрешностей передач переводятся из линейных единиц в угловые (22, 24).
3.3.3. Рассчитываются координаты середин полей рассеяния и поля рассеяния кинематических погрешностей передач (26, 28).
3.3.4. Рассчитывается координата середины поля рассеяния кинематической погрешности цепи (30).
3.3.5. При вероятностном расчете выбирается процент риска.
3.3.6. Рассчитывается значение кинематической погрешности цепи:
по методу максимума — минимума (31);
по вероятностному методу (33).
3.4. Расчет мертвого хода
3.4.1. Рассчитываются максимальные и минимальные значения мертвого хода передач, составляющих кинематическую цепь (15-21).
3.4.2. Максимальные и минимальные значения мертвого хода передач переводятся из линейных единиц в угловые (23, 25).
3.4.3. Рассчитываются координаты середин полей рассеяния и поля рассеяния мертвого хода передач (27,29).
3.4.4. Рассчитывается координата середины поля рассеяния мертвого хода кинематической цепи (30).
3.4.5. При вероятностном расчете выбирается процент риска.
3.4.6. Рассчитывается значение мертвого хода кинематической цепи:
по методу максимума — минимума (32);
по вероятностному методу (35).
|
Таблица 1 Значение коэффициента фазовой компенсации. Зубчатая передача | |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||