Рекомендации по расчету точности сборки конструкций зданий
Купить бумажный документ с голограммой и синими печатями. подробнее
Цена на этот документ пока неизвестна. Нажмите кнопку "Купить" и сделайте заказ, и мы пришлем вам цену.
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
В документе приведены основные положения по расчету точности сборных железобетонных конструкций зданий, рекомендации по технологическому
обеспечению различных классов точности при производстве геодезических разбивочных и монтажных работ, даны примеры расчетов точности сборки конструкций и уравнений погрешностей для определения параметров точности. Для инженерно-технических работников проектных и строительных организаций.
Оглавление
Введение
1. Общие положения
2. Теоретические основы расчета точности
3. Методические положения по расчету точности сборки конструкций
4. Монтаж конструкций
5. Технологическое обеспечение классов точности при монтаже
Приложение 1. Методические примеры расчетов передаточного отношения
Приложение 2. Расчеты точности сборки конструкций
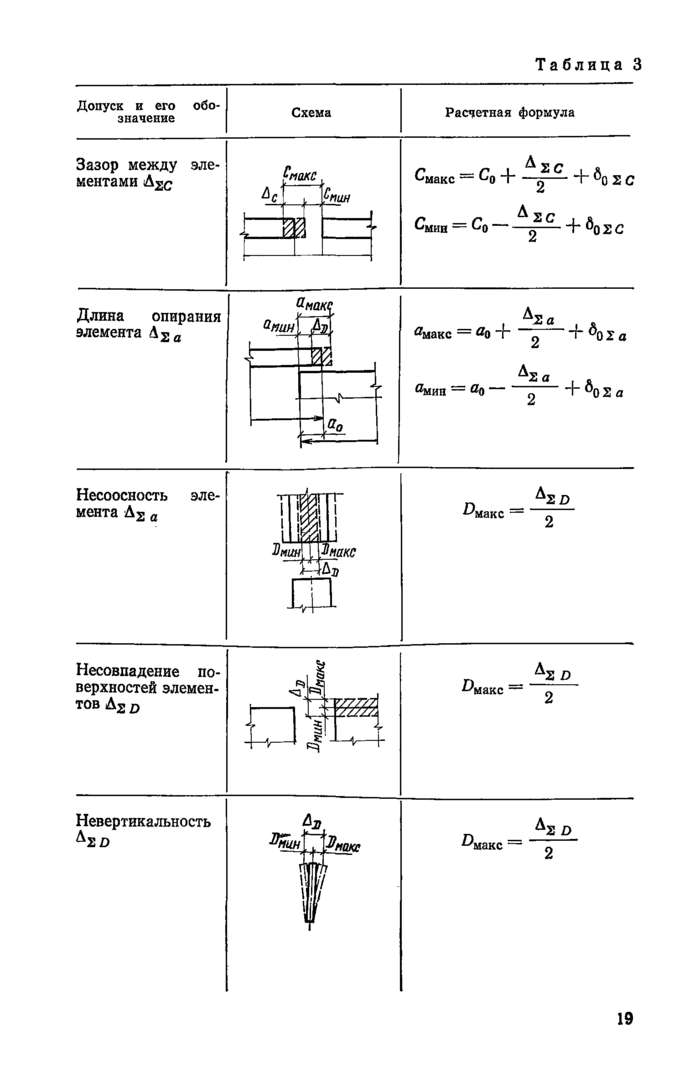
Приложение 3. Расчетные формулы и параметры точности установки элементов
Приложение 4. Статистические методы исследования и анализа точности монтажа конструкций
Приложение 5. Система технологических допусков
| Дата введения | 01.01.2021 |
|---|---|
| Добавлен в базу | 01.10.2014 |
| Актуализация | 01.01.2021 |
Этот документ находится в:
- Раздел Строительство
Организации:
| Разработан | ЦНИИОМТП Госстроя СССР | ||
| Издан | Стройиздат | 1983 г. | |
| Утвержден | ЦНИИОМТП Госстроя СССР |
- ГОСТ 21778-81 Система обеспечения точности геометрических параметров в строительстве. Основные положения
- ГОСТ 21779-82 Система обеспечения точности геометрических параметров в строительстве. Технологические допуски
- ГОСТ 23615-79 Система обеспечения точности геометрических параметров в строительстве. Статистический анализ точности
- ГОСТ 23616-79 Система обеспечения точности геометрических параметров в строительстве. Контроль точности
- ГОСТ 21780-2006 Система обеспечения точности геометрических параметров в строительстве. Расчет точности
- Показать все
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19
стр. 20

стр. 21

стр. 22
стр. 23

стр. 24
стр. 25
стр. 26

стр. 27
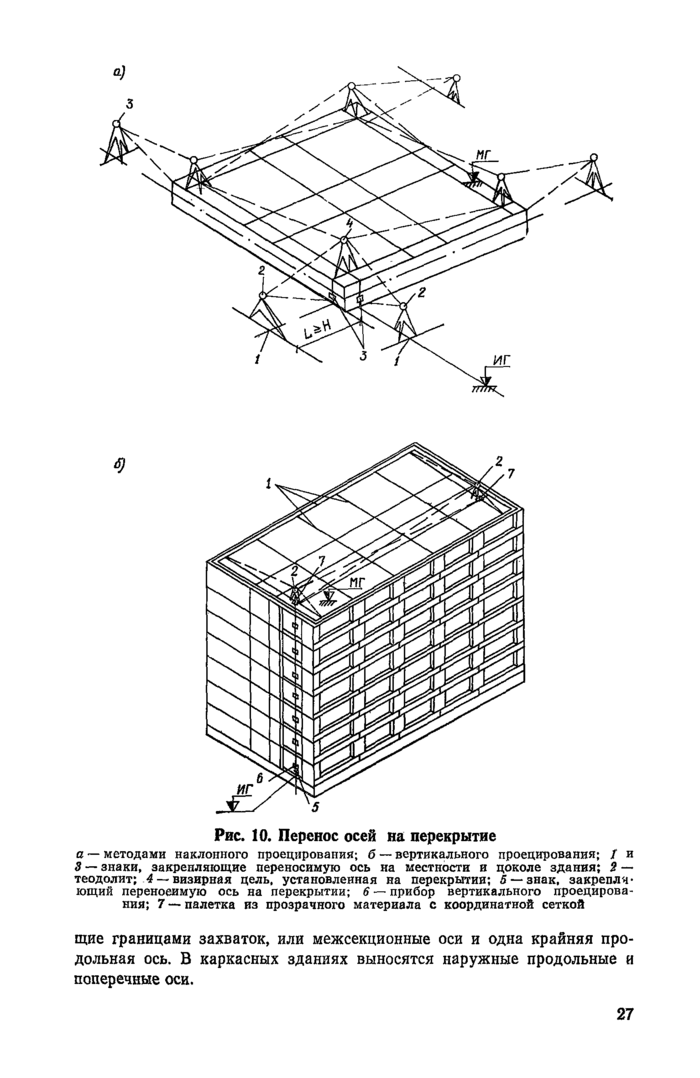
стр. 28

стр. 29

стр. 30
Рекомендации
|
по расчету точности сборки конструкций зданий |
ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ И ПРОЕКТНО-ЭКСПЕРИМЕНТАЛЬНЫЙ ИНСТИТУТ ОРГАНИЗАЦИИ, МЕХАНИЗАЦИИ И ТЕХНИЧЕСКОЙ ПОМОЩИ СТРОИТЕЛЬСТВУ (ЦНИИОМТП) ГОССТРОЯ СССР
Рекомендации
по расчету
точности
сборки
конструкций
зданий
Москва Стройиздат 1983
a2 = ]f 2 A' ■
(16>
(16>
2.25. Если бы в рабочих чертежах и технических условиях на кон-арукции указывались характеристики Мх и <х< распределения, было би целесообразно положить их в основу расчета цепей погрешностей.
Но так как характеристиками геометрической точности, приме-шемыми в чертежах и технических условиях, являются допуск А или допускаемое отклонение б и координата середины поля допуска б<ъ характеристики Mxt и неудобны для этой цели.
2.26. В отношении определения координаты середины поля допуска, соответствующей разности между средним значением эмпирического распределения и номинальным размером, применимы зависимость (15), пользуясь которой можно записать
п
г = 2 ^ i » (17)
/==1
где б02 и боа — соответственно координаты середины полей суммарного и составляющих допусков.
2.27. Для определения правила суммирования допусков воспользуемся уравнением (16), в котором обе части умножим на б2,
Г~п-
б<>2= у 2А*62°2‘ •
м
Принимая во внимание, что 6а = А, получим
As = 1/ 2 А, Д? . (18)
Уравнения (17) и (18) являются основными при расчетах точности конструкций.
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ
2.28. Рассеивание погрешностей изготовления и монтажа конструкций подчиняется определенным законам.
Законом распределения называют зависимость между возможными значениями Х\, х2,.., хк, случайной переменной и соответствующими вероятностями plt р2,..., рк
px = y = f (■*) •
2.29. Для непрерывных случайных величин, какими являются погрешности изготовления и монтажа конструкций, закон распределения
задается так называемой плотностью вероятности или дифференциальной функцией распределения, представляющими собой предел отношения попадания случайной величины х в интервал (х, х -f- Ах) к длине этого интервала Ах, когда она стремится к нулю.
2.30. Многочисленными исследованиями установлено, что рассеяние погрешностей изготовления и монтажа конструкций в большинстве своем подчиняется закону нормального распределения (закону Гаусса).
Закон нормального распределения характеризуется кривой, имеющей симметричную колоколообразную форму.
(х—х)* 2 а*
(19)
Уравнение кривой нормального распределения:
где у — плотность вероятности (величина ординаты); х — случайная величина; х — среднее значение случайной величины (центр распределения); а —среднее квадратическое отклонение случайной величины; е = 2,71828 (основание натуральных логарифмов); п = 3,14159... (постоянная величина).
2.31. Распределенные по нормальному закону погрешности характеризуются следующими свойствами:
малые по величине погрешности встречаются чаще, чем большие;
отрицательные и положительные погрешности, равные по абсолютной величине, встречаются одинаково часто;
среднее арифметическое из случайных погрешностей с увеличением их числа стремится к нулю.
2.32. Форма кривой нормального рассеивания, а также диапазон рассеивания зависят от величины среднего квадратического отклонения случайных величин погрешностей а. При увеличении <г кривая сплющивается, растягиваясь вдоль оси абсцисс. При уменьшении величины а высота кривой увеличивается и кривая сжимается по оси абсцисс (рис. 3).
2.33. Систематические погрешности на форму кривой не влияют, а вызывают смещение поля рассеивания (центра группирования) на величину, равную алгебраической сумме систематических погрешностей (рис. 4). Вся площадь, ограничиваемая кривой и осью абсцисс, равна вероятности того, что случайная величина (например, погрешность размеров) лежит в интервале от — оо до -f* оо. Эта площадь принимается равной 1 или 100%.
2.34. Вероятность (Р) того, что случайная величина х примет значения в любом интервале от некоторого значения Х\ до х2 определяется по формуле
|
И |
f* _ <*“-*)*
г — О л!
Рис. 4. Влияние х на положение кривой относительно начала координат
|
Рис. 3. Влияние величины о на форму кривой нормального распределения |
долях
X — X
а
Для удобства расчетов случайную величину х выражают в
среднего квадратического отклонения, для чего обозначают через /, тогда выражение (20) примет следующий вид:
1 U —
Р (*1 < х < ха) = у—- | е 2 d t. (21)
В приведенном выражении новые пределы интегрирования
(i = ~~1~а и t2 = а заменили пределы Х\ и х*
Правую часть уравнения (21), можно представить в виде суммы двух интегралов:
. (22)
__t±
t _tj_
2.35. Интеграл - 1__\ е 2 ^/ = Ф(/) носит название норми-
е 2 dt
J"
рованной функции Лапласа и его значения для различных t
=-—.приведены в литературе по математической статистике. Функ-
о
ция нечетная, следовательно Ф(—1)=—Ф(0 и для отрицательных значений t табличные данные берутся со знаком минус. В ряде случаев в таблицах приводятся двойные значения функции, т. е. Ф\ (/) = = 2Ф(0.
2.36. Таким образом, вероятность того, что случайная величина, подчиняющаяся закону нормального распределения, при испытаниях примет значения в пределах Х\—х2 может быть записана через Ф(/) следующим образом:
Р (х1<х<ха)=Ф (*а)-Ф Ui)=® (23)
В табл. 1 приведен ряд значений функций Ф(0 и <I>i (/) •
12
|
Таблица 1 | ||||||||||||||||||||||||||||||||||||||||
|
2.37. В технике, в том числе и в строительстве, принято диапазон рассеивания случайных погрешностей ограничивать зоной кривой, равной ±3а=6а(*=3).
Площадь, ограничиваемая кривой и осью абсцисс за пределами ±3а, равна 1—0,9973=0,0027 площади всей кривой и расположена симметрично по 0,00135 или по 0,135% с каждой стороны кривой.
Это значит, что при допуске, равном 6а, 99,73% конструкций, изготовленных или смонтированных при постоянных условиях, будут иметь размеры, находящиеся в пределах допуска, а примерно 0,27% конструкций будет иметь погрешность, превышающую ±3а.
2.38. В общем случае относительное количество элементов q, %, имеющих погрешность, превышающую dbaa, можно определить по формуле
q = [0,5 — Ф (г)) 2*100.
2.39. Если две случайные величины Xt и хг, каждая в отдельности, имеют нормальное распределение с параметрами х\ и Хг и af=a^=a2, то модуль разности этих величин
г=\х 1 — Хг\,
имеет распределение, которое носит название закона распределения модуля разности. Этому закону распределения, например, подчиняются невертикальность, несоосность и отклонения осей элементов при монтаже от проектного положения, непараллельность граней, овальность, конусность, смещения закладных деталей, выступов и гнезд изготовленных элементов, если не учитывается направление отсчета (знак отклонения) и плоскость отсчета фиксирована.
13
2.40. Плотность вероятности или дифференциальная функция распределения случайной величины г выражается следующим уравнением:
(24)
где x=\xi—Xz\ и о являются параметрами распределения модуля разности г.
При замене переменных через р = — , d р =-d г получаем
<*о
следующее выражение ф (Р) =
а 1/2
/2 л \е
(Р — Ро)8
<*0 (Р + Ро)»
4-е
]•
(25)
X
где ро= — является нормированным параметром распределения
модуля разности.
2.41. Вид кривой распределения <р(р) зависит от значения р0. При ро=0 кривая резко асимметрична, при р0=3 она совпадает с кривой нормального распределения (рис. 5).
2.42. Определение предельного отклонения р, аналогичного для закона нормального распределения производится по формулам:
или
F (Р) = 1ф (р —ро) +Ф (Р + Рв)1. (26) где каждое из двух слагаемых Ф (/) является интегралом вероятности Лапласа.
2.43. Если дано непосредственное распределение случайной величины модуля разности г и могут быть определены параметры этого распределения г и аг, то р0 может быть определено через параметр распределения (нормированное среднее)
|
Рис. 5. Вид кривых распределения модуля точности при р=0; 1,6 и 3 |
Яо=-7. (27)
Значения р0 для случайных величин Яо приведены на графике рис. 39. Пользуясь ими, по найденному р0 можно определить о(р) и все основные параметры распределения модуля разности, причем
а =
о (г)
(28)
и х = ар0. (29)
В прил. 2 приведены примеры расчета параметров распределения модуля разности.
14
3. МЕТОДИЧЕСКИЕ ПОЛОЖЕНИЯ ПО РАСЧЕТУ ТОЧНОСТИ СБОРКИ КОНСТРУКЦИЙОБЩИЕ ПОЛОЖЕНИЯ
3.1. Расчет точности состоит из определения суммарных характеристик точности замыкающих звеньев размерных цепей (целей погрешностей) конструкций и их элементов, в которых компенсируются погрешности технологических процессов и операций.
3.2. Расчет производится на основе выявления в конструктивнотехнологических схемах цепей погрешностей конструкций или элементов, непосредственно влияющих на собираемость, составления уравнения погрешностей (точности) и решения этого уравнения из условия соответствия суммарных характеристик точности замыкающих звеньев функциональным требованиям.
3.3. Замыкающим называется звено цепи погрешностей в технологической последовательности, размеры и точность которого зависят от размеров и точности всех остальных звеньев цепи.
Замыкающими звеньями размерных цепей конструкций служат, как правило, размеры в узлах сопряжений элементов, размеры зазоров между элементами, длины опиранйя элементов, несоосность или уступ элементов, невертикальность элементов.
3.4. Все остальные звенья цепи погрешностей, определяющие размеры и точность замыкающего звена, называются составляющими.
3.6. Задача расчета точности может быть: прямой, когда по известным значениям технологических допусков определяется функциональный допуск (проверочный расчет); обратной, когда по установленному функциональному допуску определяются технологические допуски (проектный расчет); комбинированной, сочетающей в себе элементы прямой и обратной задач.
МЕТОДИЧЕСКИЕ ПРИНЦИПЫ РАСЧЕТА ТОЧНОСТИ
3.6. Расчет точности конструкций должен производиться, как правило, из условия полной собираемости конструкций, при которой:
— ^2
■*макс *о ^ 2 ^0 2 ♦ (30)
д2
*мин *о ^ 2 “Ь^0 2 (31)
или при симметричных допусках
Д2 > лф , (32)
где Хмакс и Хмяв — наибольшее и наименьшее предельные значения размера, служащего замыкающим звеном, которые определяются рас-
15
Рекомендованы к изданию решением секции технологии строительного производства Научно-техничеокого совета ЦНИИОМТП.
Рекомендации по расчету точности сборки конструкций зданий / /ЦНИИОМТП.—М.: Стройиздат, 1983.— 135 с.
Приведены основные положения по расчету точности сборных железобетонных конструкций зданий, рекомендации по технологическому обеспечению различных классов точности при производстве геодезических разбивочных и монтажных работ, даны примеры расчетов точности сборки конструкций и уравнений погрешностей для определения параметров точности.
Для инженерно-технических работников проектных и строительных организаций.
Табл. 40, ил. 38.
Разработаны ЦНИИОМТП Госстроя СССР (канд. техн. наук Р. А. Каграманов при участии инж. С. Ц. Мкртчяна).
3204000000—437
047(01)—83
Инструкт.-нормат., II вып. — 103—83
© Стройиздат, 1983
ВВЕДЕНИЕ
В сборном строительстве проблема обеспечения качества неразрывно связана с обеспечением геометрических параметров точности сборки.
С геометрическими параметрами связаны такие важные эксплуатационные показатели конструкций, как их несущая способность и долговечность, звуко-, водо- и воздухонепроницаемость стыков, обеспечение эстетических требований и комфортности.
В настоящее время сборка конструкций зданий часто производится с отступлениями от требований проектов и норм. Одной из причин такого положения является назначение проектировщиками допусков на изготовление и монтаж элементов без расчетного обоснования, их увязки между собой и с функциональным допуском, без учета технических возможностей производства и особенности монтируемых конструкций.
Гарантия обеспечения определенного качества конструкций по геометрическим параметрам потребовала разработки комплекса стандартов (ГОСТ 21778-81, 21779—76, 21780—76, 23615—79 и 23616—79), составляющих систему обеспечения геометрической точности в строительстве, которыми устанавливаются общие правила расчета и назначения допусков, номенклатура и числовые значения технологических допусков.
Государственными стандартами введен ряд требований, обязывающих проектировщиков назначать допуски на основе расчета точности сборки конструкций, который должен стать неотъемлемой частью каждого типового и экспериментального проекта зданий и сооружений. Эти расчеты должны производиться методами, основанными на математической статистике и теории вероятностей.
1* Зак. 489
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Настоящие Рекомендации содержат основные положения по расчету геометрической точности сборки конструкций многоэтажных жилых и каркасных промышленных и общественных зданий.
1.2. Расчет геометрической точности сборки конструкций необходимо Производить для обеспечения на стадии проектирования собираемости конструкций с заданными эксплуатационными свойствами при наименьших материальных и трудовых затратах.
1.3. Расчет точности должен выполняться в процессе проектирования типовых, экспериментальных и индивидуальных конструкций зданий и сооружений и их элементов при назначении их номинальных размеров (в том числе размеров компенсаторов), разработке технологии изготовления элементов и конструкций и производства строительномонтажных работ.
1.4. В соответствии с результатами расчетов точности в рабочих чертежах конструкций и элементов зданий и в нормативно-технических документах устанавливаются номинальные размеры и предельные отклонения размеров элементов и узлов их сопряжений в конструкциях; в технологической документации на изготовление элементов и в проектах производства строительно-монтажных работ устанавливаются последовательность и способы выполнения разбивочных и сборочных работ, а также предусматриваются необходимые средства технологического обеспечения и контроля точности.
1.6. Собираемость конструкций может быть обеспечена конструктивными и технологическими мерами.
1.6. Основными конструктивными мерами по обеспечению собираемости конструкций являются назначения:
номинальных размеров элементов с учетом допускаемых отклонений при их изготовлении и монтаже;
размеров компенсаторов в узлах сопряжений элементов (зазоров, площадок опирания и т. п.), позволяющих компенсировать накопляемые в процессе изготовления и монтажа технологические погрешности, исключающие недопустимые контакты между элементами и обеспечивающие надежное заполнение зазоров в соответствии с проектом;
основных расчетных характеристик конструкций (несущей способности, сопротивления теплопередаче и т. п.) с учетом обеспечения качеств конструкции при предельных отклонениях геометрических параметров, влияющих на данное качество.
1.7. Основными технологическими мерами по обеспечению собираемости конструкций являются:
проектирование технологии производства работ, проектирование и изготовление технологической оснастки и формовочного оборудования, а также организация службы контроля, обеспечивающих изготовление изделий с заданными геометрическими параметрами;
проектирование технологии производства работ, проектирование и
4
изготовление монтажной оснастки, оборудования, приспособлений и инструмента, обеспечивающих соблюдение заданной точности при сборке конструкций;
разработка и применение методов и средств геодезических измерений, обеспечивающих заданную точность измерений, при разбивке, выверке и приемке конструкций.
1.8. Нахождение оптимального соответствия между технологическими и конструктивными мерами обеспечения собираемости конструкций, при которых обеспечивался бы минимум стоимости конструкции «в деле», является конечной и основной задачей расчета точности сборки конструкций и их элементов.
1.9. Подобная задача решается при разработке новых конструкций. Она связана с исследованием изменения функциональных (эксплуатационных) характеристик конструкций, в том числе их несущей способности при различных значениях технологических допусков.
В данном случае нахождение оптимального соответствия между конструктивными и технологическими мерами обеспечения собираемости конструкций и соответствующими допусками должно быть основано на сопоставлении дополнительных затрат, связанных с повышением точности изготовления и монтажа конструкций, с эффектом, достигаемым благодаря этому и связанным с экономией материалов в результате уменьшения сечения элементов, сокращения расхода стали, герметиков при устройстве стыков и т. п.
1.10. В том случае, когда физико-механические характеристики применяемых материалов, требования обеспечения прочности и комфортности не позволяют повысить собираемость конструкций за счет конструктивных мер, решается более ограниченная задача — нахождение такого соотношения между величинами технологических допусков, регламентирующих точность выполнения процессов по стадиям производства (изготовления, геодезической разбивки и монтажу элементов), при котором достигался бы минимум затрат на обеспечение суммарного технологического допуска.
2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАСЧЕТА ТОЧНОСТИ
2.1. Действительные размеры конструкций никогда не совпадают с номинальными (проектными), так как выполнение каждой технологической операции при изготовлении и монтаже конструкций неизбежно сопровождается погрешностями.
При этом под действительным понимается размер, установленный измерением с допустимой погрешностью.
2.2. Погрешности, возникающие при изготовлении и монтаже конструкций, по характеру их происхождения могут быть разбиты на две группы: систематические и случайные.
2.3. Систематические погрешности возникают под влиянием постоянно действующего фактора и не изменяются в процессе выполне-
5
ния технологического процесса. Они входят в случайную погрешность с постоянным знаком.
2.4. Случайные погрешности непостоянны по величине и знаку и возникают под влиянием случайных, изменяющихся в процессе выполнения технологического процесса факторов. Отнесение погрешности к тому или иному виду зависит от конкретных условий. Так, например, для погрешности партии сборных элементов, изготовленных в одной форме, имеющей погрешность х, последняя будет рассматриваться как систематическая составляющая. Однако, если рассматривать партию одноименных элементов, изготовленных в нескольких формах, то погрешности форм проявятся как случайные погрешности. То же самое можно сказать в отношении погрешностей монтажа. Например, погрешность установки базового элемента при ограниченно свободном монтаже проявится как систематическая погрешность для элементов, установленных в данной цепи. Однако она будет носить случайный характер, если рассматривать погрешности установки элементов в разных цепях, для каждой из которых будет свой базовый элемент.
2.6. Точность геометрических параметров в строительстве определяется установленными ГОСТ 21778-81 характеристиками действительной и нормативной точности.
ДЕЙСТВИТЕЛЬНАЯ ТОЧНОСТЬ
2.6. Характеристикой действительной точности каждого отдельно взятого размера служит величина действительного отклонения б* характеризующая степень приближения действительного размера к номинальному, что выражается следующей формулой:
о, (1)
где Х{ — действительный размер; хо — номинальный размер.
2.7. Действительное отклонение является количественным выражением систематических и случайных погрешностей, сопровождавших выполнение данного размера.
2.8. Оценку точности размеров в массовом производстве производят на основе изучения распределения размеров (или распределения погрешностей) и определения статических характеристик.
2.9. Совокупность значений погрешностей, расположенных в возрастающем порядке с указанием их вероятностей, называется распределением погрешностей.
2.10. Различают теоретические и эмпирические распределения погрешностей.
2.11. В теоретических распределениях оценка возможных значений погрешности производится при помощи вероятностей, а в эмпирических— при помощи частот или частостей, полученных в результате измерений. Следовательно, эмпирическим распределением погрешностей называется совокупность наблюденных значений их, расположен-
6
ных в возрастающем порядке, с указанием соответствующих частот или частостей.
2.12. О эмпирическом распределении случайной погрешности судят на основе выборочного наблюдения — выборки. Совокупность, из которой производится выборка, называется генеральной совокупностью. Объем N генеральной совокупности при изучении технологических процессов можно считать бесконечным. Объем п выборки всегда конечен.
|
Рис. 1. Теоретическая кривая нормального распределения и характеристики действительной точности (без скобок —для генеральной совокупности объемом V; в скобках — для выборочной совокупности объемом п) |
2.13. Чем больше объем выборки, тем точнее она отображает распределение изучаемого признака в генеральной совокупности. Результаты обработки выборочной совокупности называют выборочными или эмпирическими. Они дают выборочные (эмпирические) сводные статистические характеристики. В отличие от них для генеральных совокупностей сводные характеристики называются генеральными или теоретическими.
2.14. Характеристиками точности генеральной совокупности из N одноименных действительных размеров Х{ являются их генеральное среднее а, координата центра группирования действительных отклонений относительно номинального размера р и среднее квадратическое отклонение а или дисперсия D (рис. 1).
Генеральное среднее а и координата центра группирования р количественно характеризуют величину систематической погрешности, а среднее квадратическое отклонение а (или дисперсия D) — поле рассеяния действительных размеров, получаемое в результате воздействия случайных факторов.
В зависимости от направления смещения центра группирования отклонений относительно номинального размера координата центра группирования може* быть величиной положительной или отрицательной.
2.15. В практике характеристики точности генеральной совокупности а, Р, о (iD) вычисляют на основе выборочных наблюдений. В этом случае характеристикам точности генеральной совокупности будут соответствовать их выборочные оценки х, 6 и 5, установленные на основе данпых выборки объемом п измерений.
ХАРАКТЕРИСТИКИ НОРМАТИВНОЙ ТОЧНОСТИ
2.16. Точность геометрических параметров в стандартах и других нормативных документах, а также в рабочих чертежах характеризуется наибольшим и наименьшим предельными размерами Хмако и Хмин, верхним и нижним предельными отклонениями 6В и 6Н, допуском А и координатой середины поля допуска б0. Предельные отклонения и
7
координата середины поля допуска по знаку могут быть как положительными, так и отрицательными величинами. Допуск является положительной величиной.
(2)
(3)
(4)
(5)
2.17. Взаимосвязь между характеристиками нормативной точности определяется формулами:
6° — *макс — *о» бн = Хит — Xq\
Л = ДГмакс *мин ИЛИ А =6° 6Н1
6В + 6Н
|
///////Л Y//S/SA1 Хмим jJ Хца*с_^ у Рис. 2. Характеристики нормативной точности (штриховкой показано поле допуска) |
Графически характеристики нормативной точности представлены на рис. 2.
ВЫВОД ОСНОВНЫХ РАСЧЕТНЫХ ФОРМУЛ
2.18. Поскольку погрешности изготовления и монтажа конструкций являются случайными величинами, в отношении их можно пользоваться всеми правилами теории вероятностей.
Для расчета размерных цепей важными являются следующие теоремы теории вероятностей.
2.19. Среднее значение (математическое ожидание) суммы случайных величин равно сумме средпих значений (математических ожиданий) этих величин.
Так, если случайная величина х может быть представлена как сумма случайных величин Ху Хъ хп, т. е.
•. .±хл, то
* = *1 + Х»+ ... +*П. (6)
Эта теорема имеет широкое применение в расчете цепей погрешностей. Величина х в этих расчетах является средним значением размера замыкающего звена, а величины ху хъ хп — средними значениями составляющих звеньев.
2.20. Дисперсия суммы (разности) нескольких независимых случайных величин равна сумме дисперсий этих величин
D (*i + х2 + ... + хп) = D (*i) -|- D (**) + ... -\-D (хп). (7)
Из равенства а(х) =|ЛD(x) следует, что среднее квадратическое отклонение суммы (разности) независимых случайных величин равно корню квадратному из суммы квадратов средних квадратических отклонений этих величин
<т (Х\ + + ... -f- хп) = *1/ a* (*i) -j- (х2) + ... + cra (хп). (8)
Формула (8) называется формулой квадратичного сложения дисперсий.
Заметим, что в правой части этой формулы стоит знак плюс независимо от того, рассматривается сумма или разность случайных величин. На правиле сложения дисперсий основаны правила суммирования допусков при расчетах цепей погрешностей.
2.21. Среднее значение произведения случайной величины на постоянную равно произведению этой постоянной на среднее значение случайной величины:
х(сх)*=сх. (9)
2.22. Дисперсия произведения постоянной величины на случайную равна произведению квадрата постоянной величины на дисперсию случайной величины
D (сх) = c2D (х). (10)
Соответственно, среднее квадратическое отклонение произведения постоянной величины на случайную равно корню квадратному из произведения квадрата постоянной величины на среднее квадратическое отклонение случайной величины:
а (сх) = 1/72 оа . (11)
2.23. Поскольку отклонения составляющих звеньев цепей погрешностей связаны в общих случаях с отклонениями замыкающих звеньев передаточными отношениями Л< при расчетах точности необходимо бывает определить по существу характеристики произведения постоянной на случайную величину, т. е. сх.
2.24. Используя приведенные выше теоремы и заменив среднее значение х на математическое ожидание М, а также постоянную величину с на передаточное отношение Л<, можно написать в общем виде:
Обозначим М AjXt) и <т(2Л<*0 через и <т2 t а также
/
ах через -сг<.
п
(15)
м£= 2 AiMxt, /=1
9