ГОСТ 8032-84
Предпочтительные числа и ряды предпочтительных чисел
Купить ГОСТ 8032-84 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Устанавливает предпочтительные числа и ряды предпочтительных чисел, которые должны применяться при установлении градаций и отдельных значений параметров технических объектов, а также ряды чисел, применяемые в случаях, когда использование рядов предпочтительных чисел невозможно или нецелесообразно. Стандарт не распространяется на параметры технических объектов, естественная закономерность изменения значений которых отличается от закономерностей образования рядов, установленных настоящим стандартом
Оглавление
1. Основные положения
2. Основные ряды предпочтительных чисел
3. Дополнительные ряды предпочтительных чисел
4. Выборочные ряды предпочтительных чисел
5. Составные ряды предпочтительных чисел
6. Приближенные предпочтительные числа
7. Производные предпочтительные ряды чисел
8. Специальные ряды чисел
9. Общие правила применения предпочтительных чисел и предпочтительных рядов чисел
Приложение 1. Свойства рядов предпочтительных чисел
Приложение 2. Предпочтительные выборочные ряды предпочтительных чисел
Приложение 3. Специальные ряды чисел и значений величины (параметра)
| Дата введения | 01.07.1985 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Экология
- Раздел 07 МАТЕМАТИКА. ЕСТЕСТВЕННЫЕ НАУКИ
- Раздел 07.020 Математика
- Раздел 07 МАТЕМАТИКА. ЕСТЕСТВЕННЫЕ НАУКИ
- Раздел Электроэнергия
- Раздел 07 МАТЕМАТИКА. ЕСТЕСТВЕННЫЕ НАУКИ
- Раздел 07.020 Математика
- Раздел 07 МАТЕМАТИКА. ЕСТЕСТВЕННЫЕ НАУКИ
Организации:
| 09.08.1984 | Утвержден | Госстандарт СССР | 450 |
|---|
Preferred numbers and series of preferred numbers
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3
стр. 4
стр. 5

стр. 6

стр. 7
стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18
стр. 19
ГОСУДАРСТВЕННЫЙ СТАНДАРТ
СОЮЗА ССР
ПРЕДПОЧТИТЕЛЬНЫЕ ЧИСЛА И РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
ГОСТ 8032-84 (СТ СЭВ 3961—83)
Цена 5 коп.
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
Москва
УДК 389.17 : 006.354 Группа Т10
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРЕДПОЧТИТЕЛЬНЫЕ ЧИСЛА И РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
ОКСТУ 0080
Preferred numbers and series of preferred numbers
7.4.1. Арифметические предпочтительные ряды чисел должны применяться при установлении значений параметров:
сумма или разность которых должна принадлежать тому же ряду (например, при блочном проектировании и модульной координации размеров);
лежащих в ограниченных пределах, в которых целесообразна линеаризация (например, интервалы температур окружающего воздуха, определяющие нормы, размеры обуви и одежды);
когда равномерная градация обусловлена удобством использования (например, значения аргументов в таблицах, градуирование шкал приборов);
когда нужны точные целые значения (например, эталонные значения параметров);
выраженных в значениях логарифмов или в децибеллах (например, нормы на уровень шума).
7.4.2. Точные значения членов арифметических рядов в интервале 0—1000 представляют собой мантиссы десятичного логарифма исходных (точных) значений предпочтительных чисел.
7.4.3. Арифметические предпочтительные ряды чисел ограничены в обоих направлениях условиями п. 7.4.
7.4.4. Предпочтительные арифметические ряды могут быть положительными и отрицательными или могут переходить через нуль.
7.4.5. При сложении или вычитании числа предпочтительного арифметического ряда дают число того же ряда, если оно не выходит за его пределы.
7.4.6. Обозначения и разности основных и дополнительных арифметических предпочтительных рядов чисел устанавливаются но табл. 6.
Таблица 6
| |||||||||||||||||||||||||||||
|
Примечание. Точные значения членов основных арифметических рядов в интервале от 0 до 1000 приведены в табл. 2 в графе «Мантисса десятичного логарифма». | |||||||||||||||||||||||||||||
ГОСТ 8032-84 Стр. 11
7.4.7. В обозначениях арифметических предпочтительных рядов чисел должны указываться их разность и числа, ограничивающие ряд, например:
А 2 (—10 . . . +Ю)
А 0,5 (0 . . . 40)
А 1250 (5-103 . . . 2-104).
7.4.8. Для арифметических предпочтительных рядов чисел сохраняются положения п. 4.1 и раздела 4 настоящего стандарта.
Примечание. Обозначение выборочных арифметических рядов образуется аналогично обозначениям выборочных рядов предпочтительных чисел по
8. СПЕЦИАЛЬНЫЕ РЯДЫ ЧИСЕЛ
8.1. В случаях, когда ряды чисел, перечисленные в разделах 1—7 не могут быть применены из-за естественной закономерности изменения значений параметра, используют специальные ряды чисел, правила построения которых приведены в справочном приложении 3.
9. ОБЩИЕ ПРАВИЛА ПРИМЕНЕНИЯ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ И ПРЕДПОЧТИТЕЛЬНЫХ РЯДОВ ЧИСЕЛ
9.1. Предпочтительные числа и их ряды должны использоваться:
при установлении стандартных значений и рядов стандартных значений величин;
при нормировании значений исходных параметров продукции, условий ее существования и процессов, а также разрешенных и допускаемых их отклонений;
при нормировании значений параметров продукции, связанных логарифмируемой зависимостью с исходными параметрами, значения которых нормируются посредством предпочтительных чисел;
при приведении значений параметров предметов и процессов (в т. ч. природных констант), если использование предпочтительных чисел не влечет выхода за пределы допускаемого отклонения.
9.2. Производные и специальные ряды чисел допускается применять только в случае, если применение рядов предпочтительных чисел невозможно или нецелесообразно.
9.3. В случае альтернативных вариантов предпочтение следует отдавать ряду, имеющему меньшее число градаций, а также основному ряду перед выборочным и составным.
9.4. Применение дополнительных рядов предпочтительных чисел и предпочтительных рядов чисел допускается только в том
Стр. 12 ГОСТ 8032-84
случае, если ряд R40 или созданный на его основе производный ряд чисел не обеспечивает требуемого числа градаций. Применение дополнительного ряда должно сопровождаться подробным обоснованием.
9.5. Не допускается образовывать составные ряды путем соединения предпочтительных рядов различных видов, например, геометрического и арифметического, комплементарного и геометрического и т. д.
ПРИЛОЖЕНИЕ 1 Справочное
СВОЙСТВА РЯДОВ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
1. Произведение или частное двух предпочтительных чисел, а также положительные или отрицательные степени чисел ряда дают предпочтительное число этого же ряда с относительной ошибкой в пределах от —1,01 до +1,26%.
2. Куб любого числа ряда R10 в два раза больше куба предыдущего числа, а квадрат — в 1,6 раза больше квадрата предыдущего числа (с относительной ошибкой до 0,1 %).
3. Члены ряда R10 удваиваются через каждые три числа, ряда R20 — через шесть, ряда R40 — через 12 членов и т. д.
4. В рядах, начиная с R10 находится число 3, 15, приблизительно равное л, т. е. длины окружности и площади круга примерно равны предпочтительным числам, если диаметр — предпочтительное число.
5. Ряд R40 включает предпочтительные числа 3000, 1500, 750 и 375, представляющие собой синхронные частоты вращения валов электродвигателей в оборотах в минуту.
6. Основные и дополнительные ряды предпочтительных чисел содержат все целые степени десяти.
ГОСТ 8032-84 Стр. 13
ПРИЛОЖЕНИЕ 2 Рекомендуемое
|
Предпочтительные выборочные ряды предпочтительных чисел | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Примечание: Использование выборочных рядов, знаменатель которых равен знаменателю основного ряда, допускается только для установления значений зависимых параметров.
Стр. 14 ГОСТ 8032-84
ПРИЛОЖЕНИЕ 3 Справочное
СПЕЦИАЛЬНЫЕ РЯДЫ ЧИСЕЛ И ЗНАЧЕНИИ ВЕЛИЧИНЫ (ПАРАМЕТРА)
1. Двоичный ряд чисел.
t-й член ряда находится из выражения
/1-2*
Применяется в вычислительной технике.
2. Форматные ряды стандартных значений линейного размера стороны листа
Данный ряд линейного размера образуется из условия, что стороны формата листа связаны соотношением а/6=26/а, т. е. меньший формат получается путем разрезания большего формата при сохранении соотношения сторон.
Отсюда выражение для i-ro члена ряда, определяющего размеры сторон листов различного формата имеет вид:
значение а выбирается из двух условий:
площадь исходного листа равна 1 м2;
ряд должен содержать линейный размер 1 м.
4 _
В первом случае а= 1/ У 2 =0,841 м.
Во втором случае а— \ м.
Отсюда форматный ряд линейного размера в мм будет в первом случае: Fb ... 1189, 841, 594, 420, 297, 210, 148, 105, 74, 52, 37, 26, 18, 13, 9 ...
Во втором случае: F* ... 1414, 1000, 707, 500, 353, 250, 170, 125, 88, 62, 44, 31, 22, 15, 11 ...
3. Ряды линейных размеров, полученные на основе «золотого сечения».
Значения линейных размеров прямоугольника с соотношением сторон на основе «золотого сечения» выбираются из соотношения:
а а + b Ъ
Х=—= 1,618 или—=0,618.
Прямоугольник с таким соотношением сторон может быть составлен из квадратов или прямоугольников с таким же соотношением сторон.
Прямоугольники «золотого сечения» позволяют разместить наибольший объем информации, они обладают максимальной эстетической ценностью и могут быть рекомендованы, например, для книг, картин, плакатов, линейных размеров различного рода экранов, панно, витрин, фасадов строительных сооружений и т. д.
Выражение для i-ro члена ряда, определяющего размеры сторон прямоугольников, полученных из исходного на основе «золотого сечения», имеет вид:
а
1,6181 *
ГОСТ 8032-84 Стр. 15
Значение а выбирается из двух условий:
площадь исходного прямоугольника равна 1 м2, или ряд должен содержать линейный размер 1 м.
В первом случае а= 1,272, и ряд линейного размера в мм имеет вид:
GB ... 2058, 1272, 785, 485, 300, 185, 115, 70, 44, 27, 17, 10 ...
Во втором случае ряд в мм имеет вид:
Ge ... 2618, 1618, 1000, 618, 382, 236, 146, 90, 56, 34, 21, 13 ...
4. Ряд значений модульного линейного размера Данный ряд линейного размера образуется из условия, что параллелепипед при делении большего размера пополам должен образовать два подобных ему параллелепипеда, линейные размеры которых соответствуют предпочтительным значениям, точно стыкуются друг с другом. Для обеспечения названного требования значения линейных размеров сторон модуля должны быть связаны соотношением:
a _b_ b 2с
b ~~ с * с ~~ а "
Отсюда выражения для i-ro члена ряда значений линейного размера имеет вид:
1,26Qi •
Из условия, что исходный объем параллелепипеда равен 1 м3, определяется следующий ряд значений линейных размеров модуля в мм (а =1,260):
Мк: ... 1260, 1000, 794, 630, 500, 397, 315, 250, 198 ...
Данный ряд может быть использован при блочно-модульном конструировании.
5. Стандартный упаковочно-модульный ряд линейного размера
Стандартный упаковочно-модульный ряд линейного размера представляет собой модификацию предпочтительного модульного ряда линейного размера.
Данный ряд для внутренних линейных размеров упаковки вместо соотноше-
ния V 2 : 1 = 1,2599 использует соотношение
VTO: 1 = 1,29152
Использование стандартного упаковочно-модульного ряда линейных размеров обеспечивает следующее:
два тела, сложенные малыми -сторонами, точно заполняют внутреннее пространство третьего, большего тела при укладке их вдоль меньшего размера этого тела;
средний и больший наружный линейные размеры тела образуются путем добавления единичной толщины стенки к внутреннему линейному размеру. Для внутренних линейных размеров ряд стандартных значений имеет вид:
Му: 1000, 775, 600, 494, 359, 279, 215, 187, 129, 100.
6. Арифметические ряды времени и углового размера
В тех случаях, когда для измерения времени используются секунды и минуты или минуты и часы, а для измерения угловых размеров — угловые градусы, минуты и секунды, могут использоваться предпочтительные специальные арифметические ряды, образованные по п. 7.4 настоящего стандарта и имеющие разности 3 и 1,5.
7. Стандартные ряды номинальной емкости электрических конденсаторов и номинального сопротивления резисторов
Стр. 16 ГОСТ 8032-84
|
Данные ряды представляют собой геометрические ряды чисел со знамена телями, приведенными в таблице. | ||||||||||||
|
Тождественны следующие выборочные ряды:
R20/5 = Е12/3 R 40/3 = Е24/3
R80/5 = Е48/3 R160/5=Е96/3
8. Д в о и ч н о-д есятичный ряд чисел
Данный ряд представляет собой последовательность чисел
101+1
...10‘, 2-10*, —2~ , 10‘+1...
т. е. ряд DD: ... 1, 2, 5, 10 ...
Ряд может быть рекомендован для норм, каждая из которых имеет самостоятельное применение, например, масштабов выполнения карт, чертежей, цены деления средств измерений.
Редактор М. А. Глазунова Технический редактор Э. В, Митяй Корректор С. И. Ковалева
Сдано в наб. 09.12.86 Подо, в печ. 24.12.86 1,25 уел. п. л. 1,25 уел. кр.*отт. 1,07 уч.-изд л.
Тираж 20 ООО Цена 5 коп.
Ордена «Знак Почета» Издательство стандартов, 123840, Москва, ГСП,
Новопресненскнй пер., д. 3.
Вильнюсская типография Издательства стандартов, ул. Миндауго, 12/14. Зак. 5438.
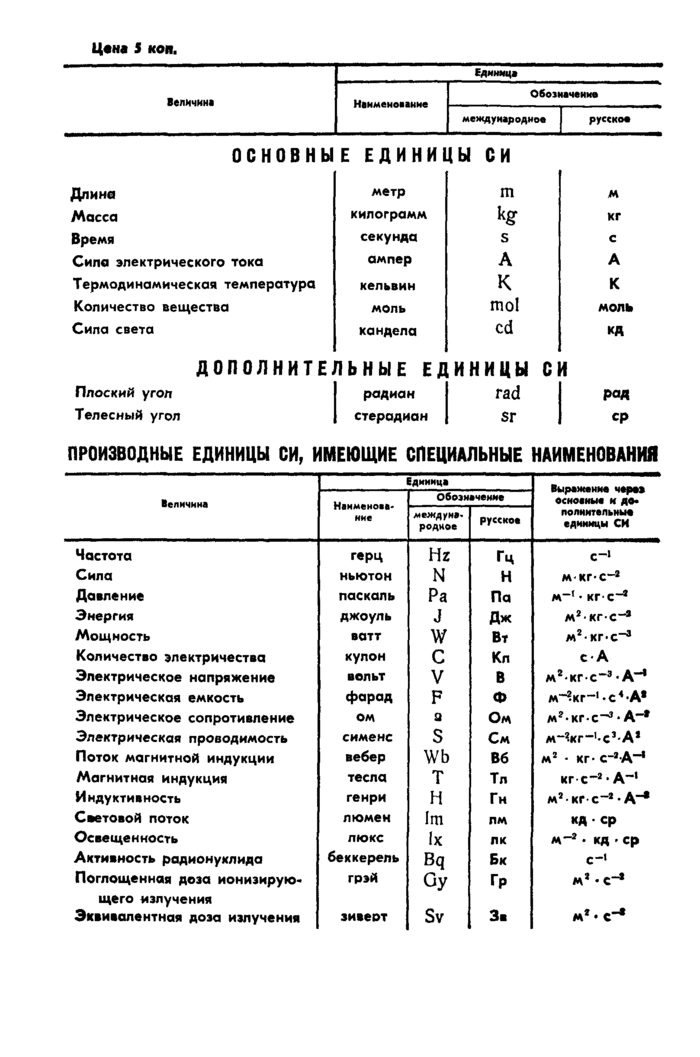
|
Величина |
Единица | ||
|
Наименование |
Обозначение | ||
|
международное |
русское | ||
|
основны |
Е ЕДИНИ1 |
1Ы СИ | |
|
Длина |
метр |
Ш |
М |
|
Масса |
килограмм |
% |
КГ |
|
Время |
секунда |
S |
С |
|
Сила электрического тока |
ампер |
А |
А |
|
Термодинамическая температура |
кельвин |
К |
К |
|
Количество вещества |
моль |
mol |
моль |
|
Сила света |
кандела |
cd |
кд |
|
ДОПОЛНИТЕЛЬНЫЕ ЕД |
1ИНИЦЫ СИ | ||
|
Плоский угол |
радиан |
rad |
рол |
|
Телесный угол |
стерадиан |
sr |
ср |
|
ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИ, ИМЕЮЩИЕ СПЕЦИАЛЬНЫЕ НАИМЕНОВАНИЯ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Значение R определяет число членов прогрессии в одном десятичном интервале.
Предпочтительные числа представляют собой округленные значения членов ряда данной прогрессии.
Члены прогрессии, расположенные в интервале от 1,00 до 10,00 составляют исходный ряд.
1.2. Ряды предпочтительных чисел не ограничиваются в обоих направлениях, при этом предпочтительные числа менее 1 и более 10 получают делением или умножением членов исходного ряда на число 10, 100, 1000 и т. д.
1.3. Предпочтительные числа одного ряда могут быть либо только положительными, либо только отрицательными.
1.4. Свойства рядов предпочтительных чисел приведены в справочном приложении 1.
2. ОСНОВНЫЕ РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
2.1. Обозначения и знаменатели основных рядов предпочтительных чисел устанавливаются по табл. 1, а члены в интервале от 1 до 10 — по табл. 2.
Таблица 1
Знаменатель ряда
Обозначение основного ряда
Точное значение <?т
Округленное значение <20
у То" 10/То
1,6
1,25
1,12
|
R 5 R10 R20 R40 1,06 40 а — у 10 Таблица 2 | ||||||||||||||||||||||||||||||||||||||||
|
20
J г
У ю
ГОСТ 8032-84 Стр. 3
|
Продолжение табл. 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2.2. При необходимости ограничения основных рядов в их обозначениях указываются предельные члены, которые всегда включаются в ограниченные ряды. Например:
Стр. 4 ГОСТ 8032-84
R10 (1,25 . . .) — ряд R10, ограниченный членом 1,25 (включи
тельно) в качестве нижнего предела;
R20 ( . . . 45) — ряд R20, ограниченный членом 45 (включительно) в качестве верхнего предела;
R40 (75 . . . 300) — ряд R40, ограниченный членами 75 и 300 и включающий оба члена.
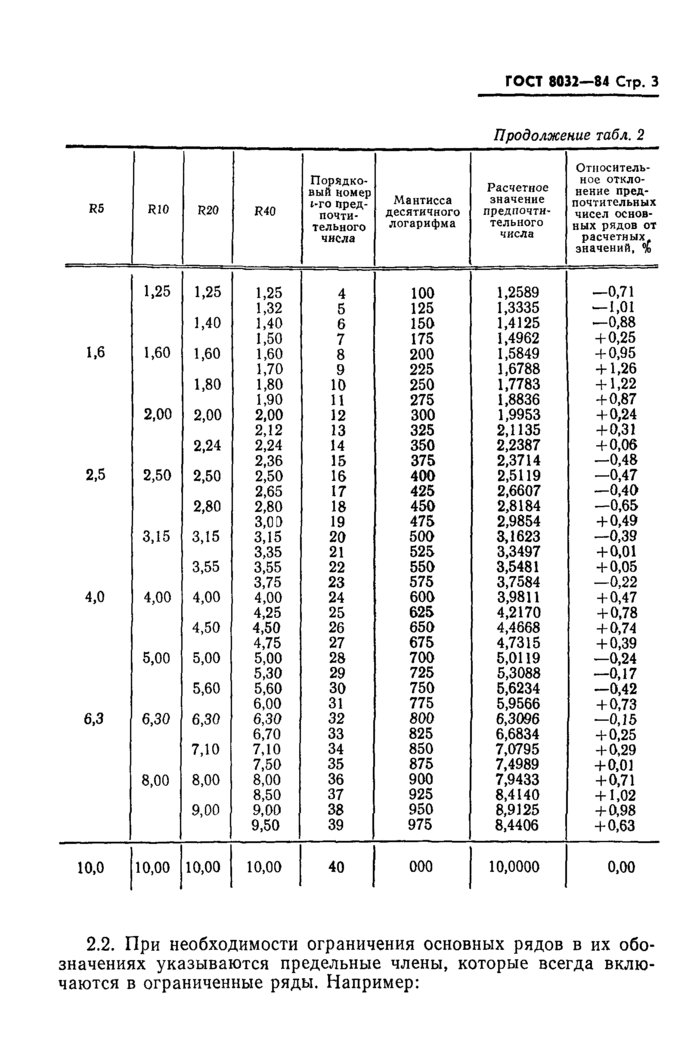
3. ДОПОЛНИТЕЛЬНЫЕ РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
3.1. Обозначения и знаменатели дополнительных рядов предпочтительных чисел устанавливаются по табл. 3, а члены в интервале от 1 до 10 — по табл. 4.
Таблица 3
|
Знаменатель ряда | ||
|
Обозначение дополнительного ряда |
Округленное значение Qc |
Точное значение |
|
R80 |
1,03 |
80/пг |
|
R160 |
1,015 |
,60/Т(Г |
|
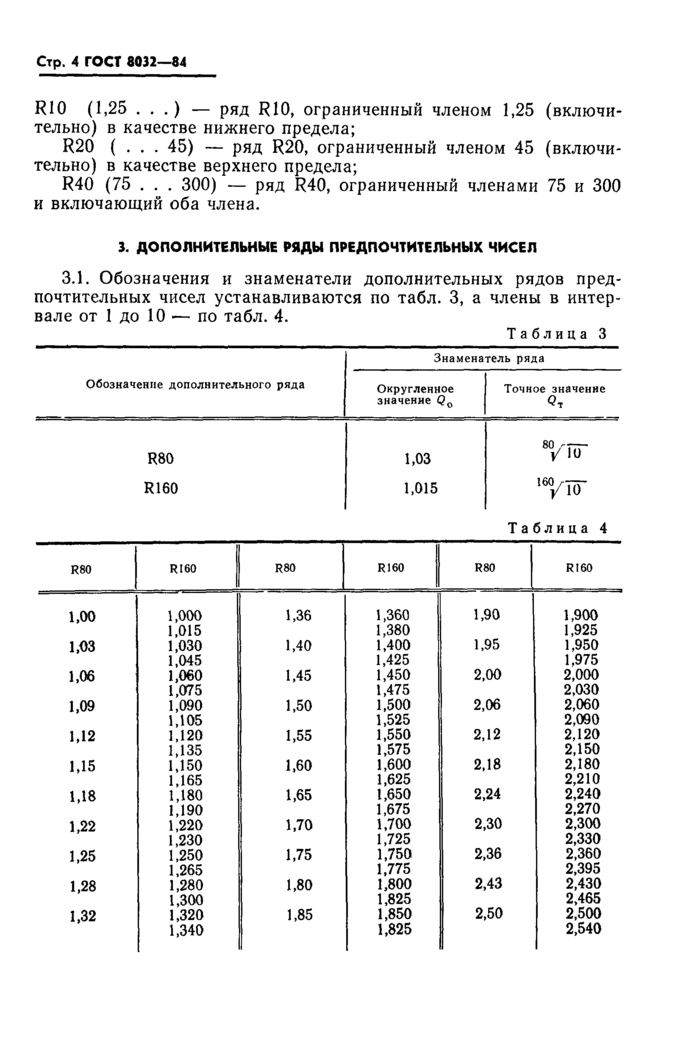
Таблица 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ГОСТ 8032-84 Стр. 5 Продолжение табл. 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3.2. Обозначения ограниченных дополнительных рядов аналогичны обозначению ограниченных основных рядов (см. п. 2.2.).
4. ВЫБОРОЧНЫЕ РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
4.1. Выборочные ряды предпочтительных чисел получают отбором каждого 2, 3, 4 . . . «-го члена основного или дополнительного ряда, начиная с любого числа ряда.
4.2. Обозначение выборочного ряда состоит из обозначения исходного основного ряда, после которого ставится косая черта и число 2, 3, 4 ... /г соответственно. Если ряд ограничен, обозначение должно содержать члены, ограничивающие ряд; если ряд не ограничен, должен быть указан хотя бы один его член, например:
Стр. 6 ГОСТ 8032-84
R 5/2 (1 .... 1000000) — выборочный ряд, составленный из каждого второго члена основного ряда R5, ограниченный членами 1 и 1000000;
R10/3 ( .... 80 ....) — выборочный ряд, составленный из каждого третьего члена основного ряда R10, включающий член 80 и не ограниченный в обоих направлениях;
R20/4 (112 ... .) — выборочный ряд, составленный из каж
дого четвертого члена основного ряда R20 и ограниченный по нижнему пределу членом 112;
R40/5 ( . . . . 60) — выборочный ряд, составленный из каж
дого пятого члена основного ряда R40 и ограниченный по верхнему пределу членом 60.
4.3. Выборочные ряды предпочтительных чисел должны применяться, когда уменьшение числа градаций создает дополнительный эффект по сравнению с использованием полных рядов. При этом предпочтение следует отдавать рядам, приведенным в справочном приложении 2.
4.4. Из выборочных рядов с одинаковым знаменателем предпочтение следует отдавать ряду, содержащему единицу или число, единственной значащей цифрой которого является единица (например, 0,01; 0,1; 10, 100 и т. д.).
5. СОСТАВНЫЕ РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
5.1. Составные ряды предпочтительных чисел получают путем сочетания различных основных и (или) выборочных рядов.
Составной ряд в различных интервалах имеет неодинаковые знаменатели.
5.2. Количество основных и выборочных рядов, используемых при получении составного ряда, должно быть минимальным.
5.3. Конечные и начальные члены смежных рядов, образующих составной ряд, должны быть одинаковыми, например:
R20 (1 . . . 2) R10 (2 . . . 10) R5/2 (10 . . . 1000)
5.4. Составные ряды предпочтительных чисел должны применяться, если требуемая плотность значений параметра в рассматриваемом интервале неодинакова.
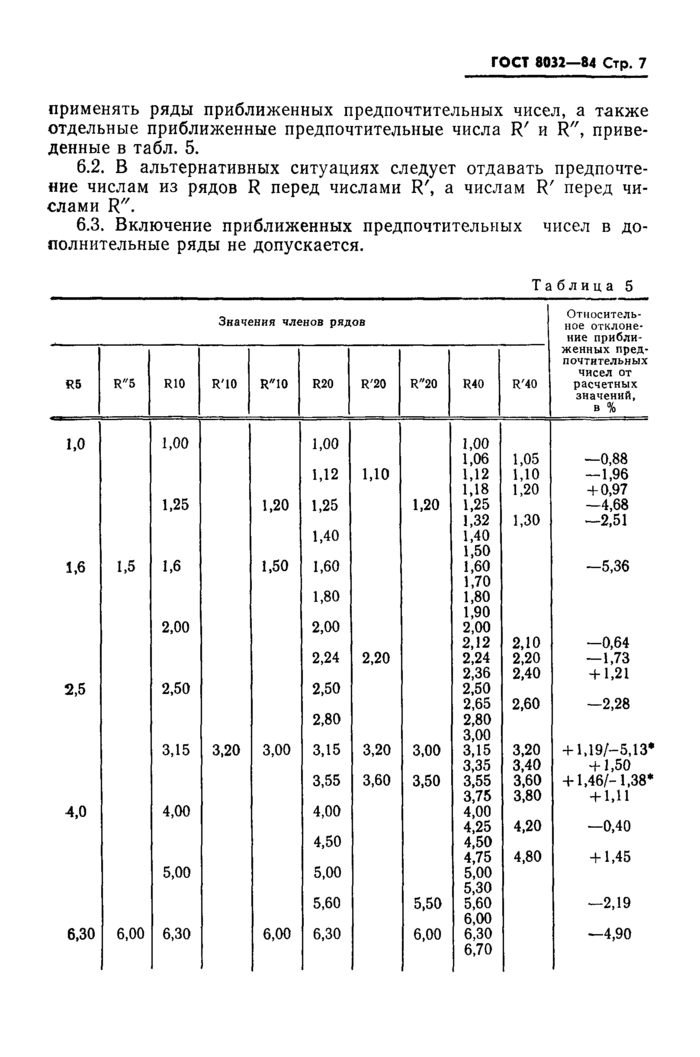
6. ПРИБЛИЖЕННЫЕ ПРЕДПОЧТИТЕЛЬНЫЕ ЧИСЛА
6.1. В обоснованных случаях вместо основных рядов предпочтительных чисел R и отдельных чисел этих рядов допускается
ГОСТ 8032-84 Стр. 7
применять ряды приближенных предпочтительных чисел, а также отдельные приближенные предпочтительные числа R' и R", приведенные в табл. 5.
6.2. В альтернативных ситуациях следует отдавать предпочтение числам из рядов R перед числами R', а числам R' перед числами R".
6.3. Включение приближенных предпочтительных чисел в дополнительные ряды не допускается.
Таблица 5
R5
1,01,6
2,5
4,0
|
R"5 1,5 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6,00
6,30
|
Продолжение табл. 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ГОСТ 8032-84 Стр. 9
7.2.1. Убывающие ряды положительных предпочтительных чисел содержат числа, приведенные в табл. 2, 4 и 5.
7.2.2. Обозначение убывающего ряда положительных предпочтительных чисел получают добавлением к обозначению каждого основного или дополнительного ряда предпочтительных чисел знака «!», например; | R5, | R10 ( . . . 1,25), | R20 (45 . . . ), | R40 (300 ... 75).
7.2.3. Для убывающих рядов положительных предпочтительных чисел сохраняются положения пп. 1.2, 1.3, 4.1 и раздела 5 настоящего стандарта.
7.3. Комплементарные предпочтительные ряды чисел получают на основе убывающей геометрической прогрессии. Выражение для r-го члена комплементарного ряда имеет вид:
#i=10m— | gi,
где т — целое число или нуль.
Для образования комплементарных рядов следует брать предпочтительные числа, приведенные в табл. 2, 4, 5 и вычитать их из 10т.
Комплементарные предпочтительные ряды чисел следует нс-пользовать для установления значений параметров, асимптотически стремящихся к 10т, например, чистоты вещества, КПД, вероятности безотказной работы.
7.3.1. Члены комплементарного ряда за некоторым исключением не есть предпочтительные числа.
7.3.2. Обозначение комплементарного ряда получают добавле
нием к обозначению исходного основного или дополнительного ряда предпочтительных чисел знака «—», например, £5, /И О (0,875 . . . ), Я 20 ( . . . 0,99955), R 40 (0,700 . . . 0,925).
7.3.3. Для комплементарных предпочтительных рядов чисел сохраняются положения п. 4.1 и раздела 5.
7.4. Арифметические предпочтительные ряды чисел получают на основе прогрессии, /-й член которой определяется выражением
= 10mlg^i = a0±——/
при условиях, что йо кратно 10m/R и
10т
йг R
<100,
где т — целое число или нуль.
Арифметический ряд предпочтительных чисел представляет собой арифметическую прогрессию с разностью D = 10m/R, причем: и сама разность, и члены ряда имеют точные значения.
Примечание. Условие, что а0 должно быть кратно 10m/R можно сформулировать так: при отсутствии ограничений арифметический предпочтительный ряд чисел должен содержать в качестве одного члена нуль.