ГОСТ Р 57949-2017
Трубы и детали трубопроводов из реактопластов, армированных стекловолокном. Методы регрессионного анализа
Купить ГОСТ Р 57949-2017 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Устанавливает два метода регрессионного анализа данных, которые при преобразовании в логарифмические значения имеют нормальное или асимметричное распределение. Стандарт применяют совместно со стандартами на методы испытаний труб и деталей трубопроводов из реактопластов, армированных стекловолокном для анализа зависимости их свойств от времени. Стандарт может быть также применен для анализа других данных. Порядок проведения испытаний для сбора данных, количество требуемых образцов и период времени сбора данных установлены в стандартах на методы испытаний труб и деталей трубопроводов из реактопластов, армированных стекловолокном.
Содержит требования ISO 10928:2009
Оглавление
1 Область применения
2 Сущность метода
3 Методика определения линейных взаимосвязей - методы А и В
4 Применение методов регрессионного анализа при испытаниях и проектировании продукции
Приложение A (обязательное) Порядок проектирования напорных труб и деталей трубопроводов из реактопластов, армированных стекловолокном
Приложение B (справочное) Полиномиальный анализ с использованием взаимосвязей второго порядка
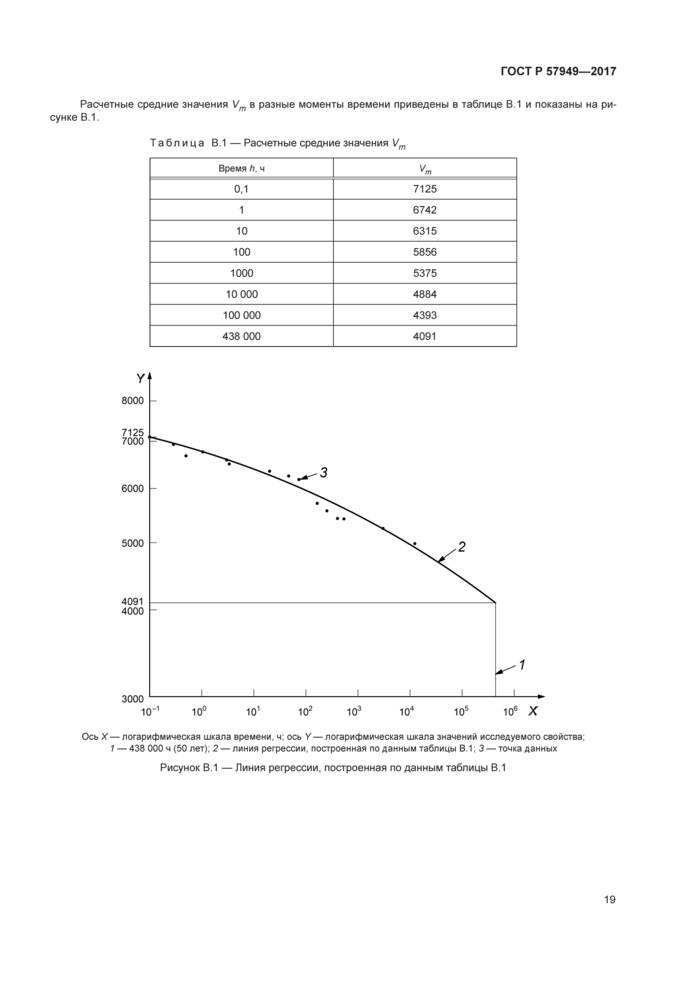
Приложение C (справочное) Нелинейный метод анализа
Приложение D (справочное) Расчет нижних границ доверительного и прогнозируемого интервалов для метода А
Приложение ДА (справочное) Оригинальный текст модифицированных структурных элементов примененного международного стандарта
Библиография
| Дата введения | 01.06.2018 |
|---|---|
| Добавлен в базу | 01.01.2019 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Экология
- Раздел Электроэнергия
- Раздел Экология
- Раздел Электроэнергия
Организации:
| 16.11.2017 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 1748-ст |
|---|---|---|---|
| Разработан | Объединение юридических лиц Союз производителей композитов | ||
| Разработан | АНО Центр нормирования, стандартизации и классификации композитов | ||
| Издан | Стандартинформ | 2017 г. |
Fiberglass-reinforced thermosetting plastics pipes and parts of pipelines. Methods for regression analysis
- ГОСТ Р 1.5-2012 Стандартизация в Российской Федерации. Стандарты национальные. Правила построения, изложения, оформления и обозначения
- ГОСТ Р 55076-2012 Трубы и детали трубопроводов из реактопластов, армированных стекловолокном. Методы определения наработки до отказа под действием постоянного внутреннего давления
- ГОСТ Р 55077-2012 Трубы и детали трубопроводов из реактопластов, армированных стекловолокном. Методы определения химической стойкости внутренней поверхности в условиях нагружения
- ГОСТ Р 54925-2012 Трубы и детали трубопроводов из реактопластов, армированных стекловолокном. Методы определения начального окружного предела прочности при растяжении
- ГОСТ 32661-2014 Трубы и детали трубопроводов из реактопластов, армированных волокном. Общие технические условия
- ГОСТ Р 54560-2015 Трубы и детали трубопроводов из реактопластов, армированных стекловолокном, для водоснабжения, водоотведения, дренажа и канализации. Технические условия
- ГОСТ Р 57006-2016 Трубы и детали трубопроводов из реактопластов, армированных стекловолокном. Метод определения долговременной удельной кольцевой жесткости при ползучести и коэффициента ползучести при воздействии влаги
- ГОСТ Р 57008-2016 Трубы и детали трубопроводов из реактопластов, армированных стекловолокном. Метод определения долговременной удельной кольцевой жесткости при релаксации и коэффициента релаксации при воздействии влаги
- ГОСТ Р 57030-2016 Трубы и детали трубопроводов из реактопластов, армированных стекловолокном. Метод определения долговременной предельной деформации изгиба и долговременной предельной относительной кольцевой деформации при воздействии влаги
- Показать все
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6
стр. 7

стр. 8
стр. 9
стр. 10
стр. 11

стр. 12
стр. 13

стр. 14

стр. 15
стр. 16
стр. 17
стр. 18
стр. 19

стр. 20

стр. 21

стр. 22
стр. 23

стр. 24

стр. 25

стр. 26
стр. 27

стр. 28
стр. 29

стр. 30
НАЦИОНАЛЬНЫЙ
СТАНДАРТ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
ГОСТР
57949—
2017
(ИСО 10928: 2009)
ТРУБЫ И ДЕТАЛИ ТРУБОПРОВОДОВ ИЗ РЕАКТОПЛАСТОВ, АРМИРОВАННЫХ СТЕКЛОВОЛОКНОМ
Методы регрессионного анализа
(ISO 10928:2009, Plastics piping systems — Glassreinforced thermosetting plastics (GRP) pipes and fittings — Methods for regression analysis and their use, MOD)
Издание официальное
Москва
Стандартинформ
2017
Предисловие
1 ПОДГОТОВЛЕН Объединением юридических лиц «Союз производителей композитов» совместно с Автономной некоммерческой организацией «Центр нормирования, стандартизации и классификации композитов» на основе собственного перевода на русский язык указанного в пункте 4 стандарта
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 497 «Композиты, конструкции и изделия из них»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 16 ноября 2017 г. № 1748-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 10928:2009 «Трубопроводы пластмассовые. Трубы и фитинги из термореактивных стеклопластиков (GRP). Методы регрессионного анализа и их применение» [ISO 10928:2009 «Plastics piping systems. — Glassreinforced thermosetting plastics (GRP) pipes and fittings — Methods for regression analysis and their use», MOD], включая изменение Amd.1:2013, путем изменения содержания отдельных структурных элементов, которые выделены вертикальной линией, расположенной на полях напротив соответствующего текста. Оригинальный текст этих структурных элементов приведенного международного стандарта и объяснения причин внесения технических отклонений приведены в дополнительном приложении ДА.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5)
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет (www.gost.ru)
© Стандартинформ, 2017
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
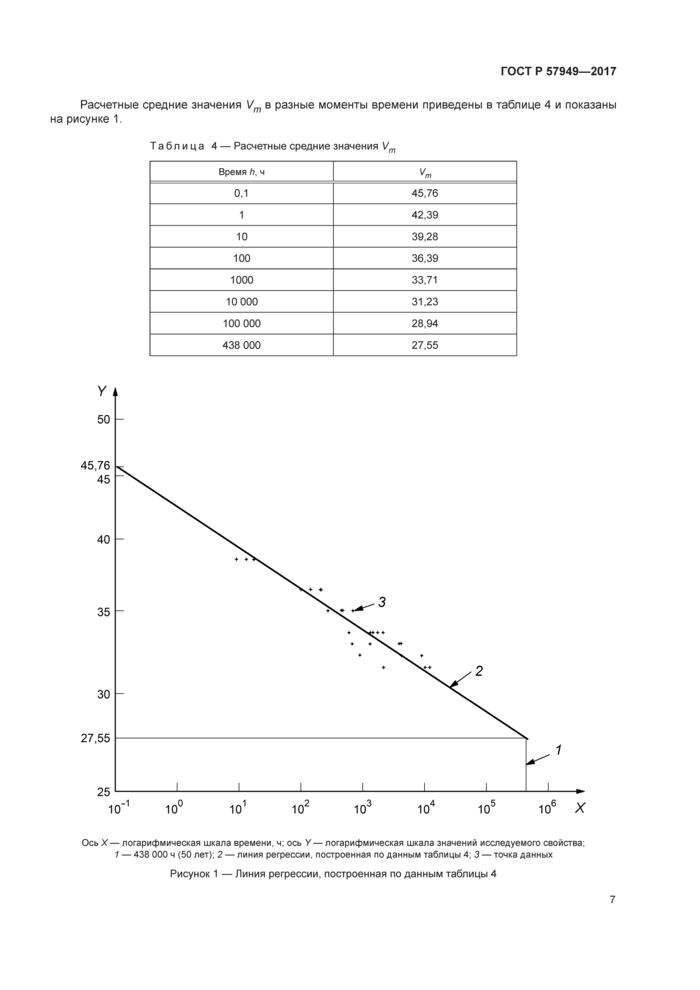
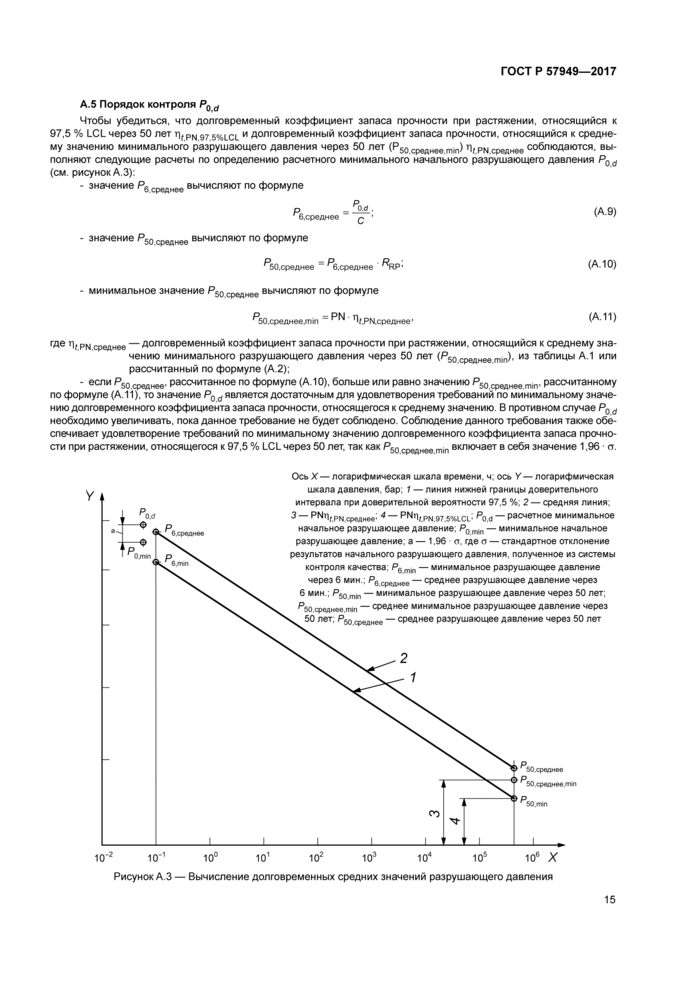
Расчетные средние значения Vm в разные моменты времени приведены в таблице 4 и показаны на рисунке 1.
|
Таблица 4 — Расчетные средние значения Vm | ||||||||||||||||||
|
|
ОсьХ—логарифмическая шкала времени, ч; ось Y—логарифмическая шкала значений исследуемого свойства; 1 — 438 ООО ч (50 лет); 2 — линия регрессии, построенная по данным таблицы 4; 3 — точка данных |
Рисунок 1 — Линия регрессии, построенная по данным таблицы 4
7
3.3 Метод В — Метод наименьших квадратов, где в качестве независимой переменной используют время
3.3.1 Общие положения
Сумму квадратов регрессионных остатков, параллельных оси У, Sy вычисляют по формуле
Sy=l{yi~Yf■ (21)
Сумму квадратов регрессионных остатков, параллельных оси X, Sx вычисляют по формуле
S, = S(x,.-X)2. (22)
Сумму квадратов регрессионных остатков, перпендикулярных прямой, Sxy вычисляют по формуле
(23)
sxy = X[(*,--x)2-(y,--y)2
Среднеарифметическое значение по всем у,-, У вычисляют по формуле (5), среднеарифметическое значение по всем xr X вычисляют по формуле (6).
Примечание — Если значение Sxyбольше нуля, угол наклона прямой b положительный, если меньше нуля — отрицательный.
3.3.2 Пригодность данных
|
S2 г2 = *У S S X у | |
|
г = | |
Квадратичный коэффициент корреляции г2 вычисляют по формуле
(24)
Линейный коэффициент корреляции г вычисляют по формуле
(25)
Данные не пригодны для анализа, если значение линейного коэффициента корреляции г меньше, чем соответствующее минимальное допустимое значение линейного коэффициента корреляции, приведенное в таблице 1, в зависимости от количества переменных п.
3.3.3 Функциональные зависимости Угол наклона прямой b вычисляют по формуле
|
(26) | |
|
Sx Точку пересечения с осью У а вычисляют по формуле а = Y- b ■ X. |
(27) |
3.3.4 Проверка пригодности к экстраполяции
Если прямую предполагается экстраполировать, вычисляют значение М по формуле
(28)
M_sl t2v(sxsy-s%)
S% (л - 2) S2
где tv— значение f-критерия Стьюдента, приведенное в таблице 2.
Если значение М меньше или равно нулю, данные не пригодны для экстраполяции.
3.3.5 Пример расчета
В таблице 5 приведены исходные данные для примера расчета метода В регрессионного анализа. В настоящем примере значение исследуемого свойства обозначено безразмерной величиной V.
|
Таблица 5 — Исходные данные для примера расчета метода В регрессионного анализа | ||||||||||
|
|
Окончание таблицы 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Суммы квадратов регрессионных остатков:
Sx = 31,6811;
Sy = 0,0347;
Sxy =-1,0242.
Коэффициент корреляции: г2 = 0,9556; г= 0,9775.
Функциональные зависимости (см. 3.3.3): а = 3,8286; b = -0,0323.
Проверка пригодности к экстраполяции (см. 3.3.4): tv= 2,1604;
М = 942,21.
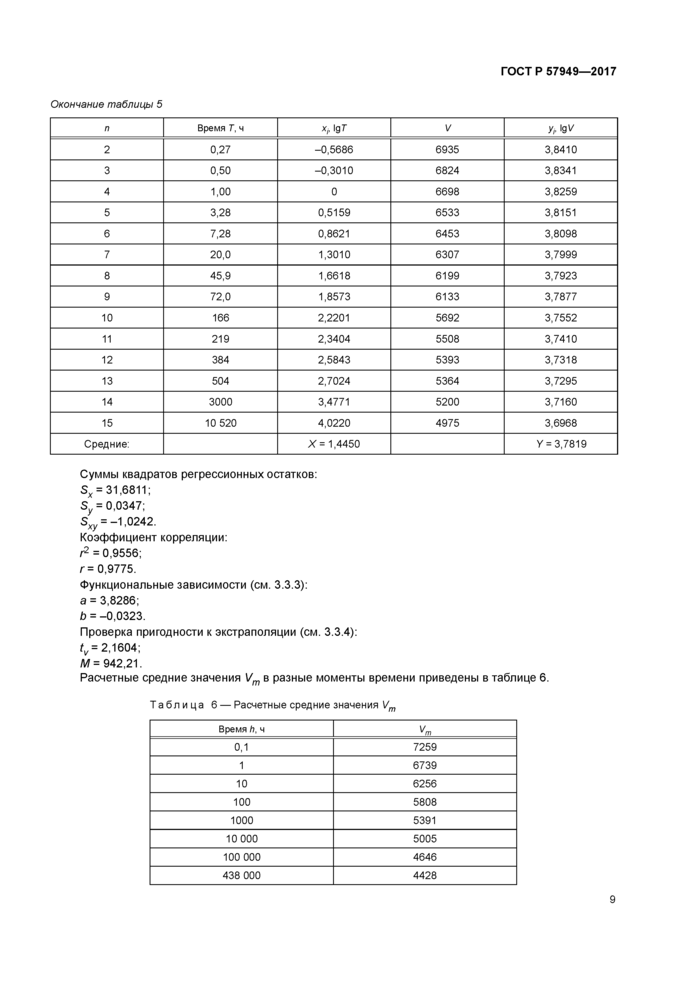
Расчетные средние значения Vm в разные моменты времени приведены в таблице 6.
|
Таблица 6 — Расчетные средние значения Vm | ||||||||||||||||||
|
9
4 Применение методов регрессионного анализа при испытаниях и проектировании продукции
4.1 Общие положения
В стандартах на методы испытаний труб и деталей трубопроводов из реактопластов, армированных стекловолокном, установлены лимитирующие требования к долговременным свойствам. Некоторые из них установлены по результатам разрушающих испытаний, например, начальный окружной предел прочности при растяжении, другие — на основании фактических или расчетных физических свойств, например долговременная удельная кольцевая жесткость при ползучести или при релаксации.
Данные свойства необходимо экстраполировать на долговременный период (например, 50 лет) для утверждения проектирования продукции или ее соответствия установленным требованиям. Экстраполированное значение Igy, используя значения а и Ь, определенные в соответствии с 3.2 или 3.3, вычисляют по формуле
Igy = а + Ь ■ fL, (29)
где tL — десятичный логарифм долговременного периода, ч [для 50 лет (438 ООО ч) fL = 5,64147].
Регрессионный анализ проводят в трех случаях в соответствии с 4.2—4.4.
4.2 Проектирование продукции
В первом случае регрессионный анализ проводят для проектирования или расчета линейки продукции. При этом используют данные долговременных испытаний на определение начального окружного предела прочности при растяжении [1]. Данные долговременных разрушающих испытаний анализируют методом А регрессионного анализа. Для проектирования также необходимо анализировать данные кратковременных испытаний [2]. Проектирование напорных труб и деталей трубопроводов из реактопластов, армированных стекловолокном, проводят в соответствии с приложением А.
4.3 Сравнение с требуемым значением
Во втором случае регрессионный анализ проводят для сравнения экстраполированного значения с минимальным требуемым значением. При этом используют данные испытаний на определение долговременной кольцевой деформации [3] и химической стойкости внутренней поверхности в условиях нагружения [4]. Данные долговременных разрушающих испытаний анализируют методом А регрессионного анализа.
4.4 Определение долговременных свойств
В третьем случае регрессионный анализ проводят для определения долговременных свойств труб и деталей трубопроводов из реактопластов, армированных стекловолокном, путем расчета экстраполированного значения, которое в дальнейшем используется производителем. При этом используют данные испытаний на определение долговременной удельной кольцевой жесткости при ползучести [5] или при релаксации [6]. Данные долговременных неразрушающих испытаний анализируют методом В регрессионного анализа.
10
ГОСТ P 57949—2017
Приложение А (обязательное)
Порядок проектирования напорных труб и деталей трубопроводов из реактопластов, армированных стекловолокном
А.1 Основные положения
Порядок проектирования, описанный в настоящем приложении, используют для определения минимальных рабочих характеристик давления для труб и деталей трубопроводов из реактопластов, армированных стекловолокном, изготовленных в соответствии с [7]. В настоящем приложении приведены рекомендуемые минимальные долговременные коэффициенты запаса прочности при растяжении относительно рабочих характеристик изделия.
Примечание — Аналогичный порядок проектирования напорных труб и деталей трубопроводов из реактопластов, армированных стекловолокном, приведен в [8] и [9].
Реактопласты, армированные стекловолокном, подвержены ползучести при прилагаемых нагрузках. Трубы и детали трубопроводов из реактопластов, армированных стекловолокном, испытывают для определения характеристик регрессионного анализа, поскольку эти характеристики зависят от технологии производства и используемого сырья.
Порядок проектирования, приведенный в настоящем приложении, основан на принципе производства, при котором трубы и детали трубопроводов из реактопластов, армированных стекловолокном, изготавливают по определенному проекту с использованием определенного технологического процесса и определенных материалов, а затем испытывают в соответствии с методом регрессионного анализа, например в [1], с аналогичными характеристиками регрессионного анализа. Данные, полученные в ходе испытаний, анализируют с помощью метода А настоящего стандарта. Угол наклона прямой, рассчитанный в результате регрессионного анализа, представляет собой общую характеристику регрессионного анализа изделий, изготовленных из аналогичных материалов с использованием аналогичных технологических процессов. Для изделий, изготовленных из аналогичных материалов с использованием аналогичных технологических процессов, характеристики регрессионного анализа сильно не отличается, то есть изделия разного диаметра и толщины дают схожие результаты.
Свойства изделий из реактопластов, армированных стекловолокном имеют внутреннюю изменчивость, но предполагается, что на производстве применяется система контроля качества, позволяющая определить коэффициент вариации и приемлемый уровень качества для начального окружного предела прочности при растяжении.
А.2 Минимальные значения долговременных коэффициентов запаса прочности
при растяжении
Большинство напорных труб и деталей трубопровода из реактопластов, армированных стекловолокном, укладывают под землей, при этом они подвергаются воздействию нагрузок от внутреннего давления и испытывают деформацию в результате нагрузки от веса грунта и движения транспорта. Учет этих комбинированных нагрузок и анализ влияния этих значений на вероятность разрушения в течение 50 лет показал, что комбинированный коэффициент запаса прочности, r|hat, должен быть не менее 1,5.
Минимальное значение кольцевой деформации зависит от жесткости трубы, которая определяет пределы деформации из-за изгиба. Зная минимальное приемлемое значение комбинированного коэффициента запаса прочности r|hat и условия изгиба, рассчитывают минимальное приемлемое значение коэффициента запаса прочности при растяжении r|f. Используя эти принципы, были рассчитаны долговременные коэффициенты запаса прочности при растяжении, относящиеся к 97,5 % LCL и средним значениям (r|fPN 97 5оЛ|_С|_ и r|f PN среднее соответственно), которые приведены в таблице А.1.
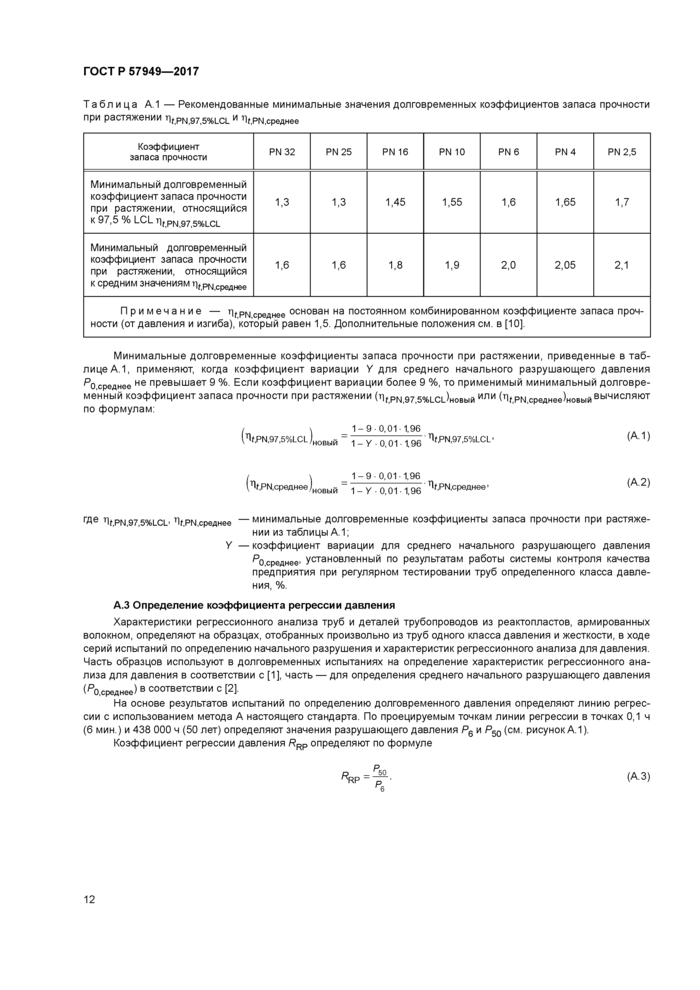
Таблица А.1 — Рекомендованные минимальные значения долговременных коэффициентов запаса прочности при растяжении TifiPNi97i5%LCL и д, PN
.среднее
|
Коэффициент запаса прочности |
PN 32 |
PN 25 |
PN 16 |
PN 10 |
PN 6 |
PN 4 |
PN 2,5 |
|
Минимальный долговременный коэффициент запаса прочности при растяжении, относящийся к 97,5 % LCL r|f рм 97 5%lcl |
1,3 |
1,3 |
1,45 |
1,55 |
1,6 |
1,65 |
1,7 |
|
Минимальный долговременный коэффициент запаса прочности при растяжении, относящийся К средним значениям Т^рм.среднее |
1,6 |
1,6 |
1,8 |
1,9 |
2,0 |
2,05 |
2,1 |
|
Примечание — r|fPNсреднее основан на постоянном комбинированном коэффициенте запаса прочности (от давления и изгиба), который равен 1,5. Дополнительные положения см. в [10]. | |||||||
Минимальные долговременные коэффициенты запаса прочности при растяжении, приведенные в таблице А.1, применяют, когда коэффициент вариации У для среднего начального разрушающего давления Р0 СредНее не превышает 9 %. Если коэффициент вариации более 9 %, то применимый минимальный долговременный коэффициент запаса прочности при растяжении (л^,РМ,97,5%1_С1_)НОвЬ1Й ИЛИ К,РМ,среднее)новый вычисляют по формулам:
(А.1)
I \ _ 1-9 0,01 1,96
l1lf,PN,97,5%LCLjHOBb|K ■1_y.0,01.1,96'11'W7’5%LCL
(А-2)
\ _ 1-9 0,01 1,96
>,PN,среднее]новь|й “ ! _ у . 0,01 Щ,96 ^'РМ'среднее
где T|fPN97 5%LCL’ 'HfPN среднее —минимальные долговременные коэффициенты запаса прочности при растяжении из таблицы А.1;
У — коэффициент вариации для среднего начального разрушающего давления Р0 среднее’ установленный по результатам работы системы контроля качества предприятия при регулярном тестировании труб определенного класса давления, %.
А.З Определение коэффициента регрессии давления
Характеристики регрессионного анализа труб и деталей трубопроводов из реактопластов, армированных волокном, определяют на образцах, отобранных произвольно из труб одного класса давления и жесткости, в ходе серий испытаний по определению начального разрушения и характеристик регрессионного анализа для давления. Часть образцов используют в долговременных испытаниях на определение характеристик регрессионного анализа для давления в соответствии с [1], часть — для определения среднего начального разрушающего давления (р0,среднее) в Соответствии С [2].
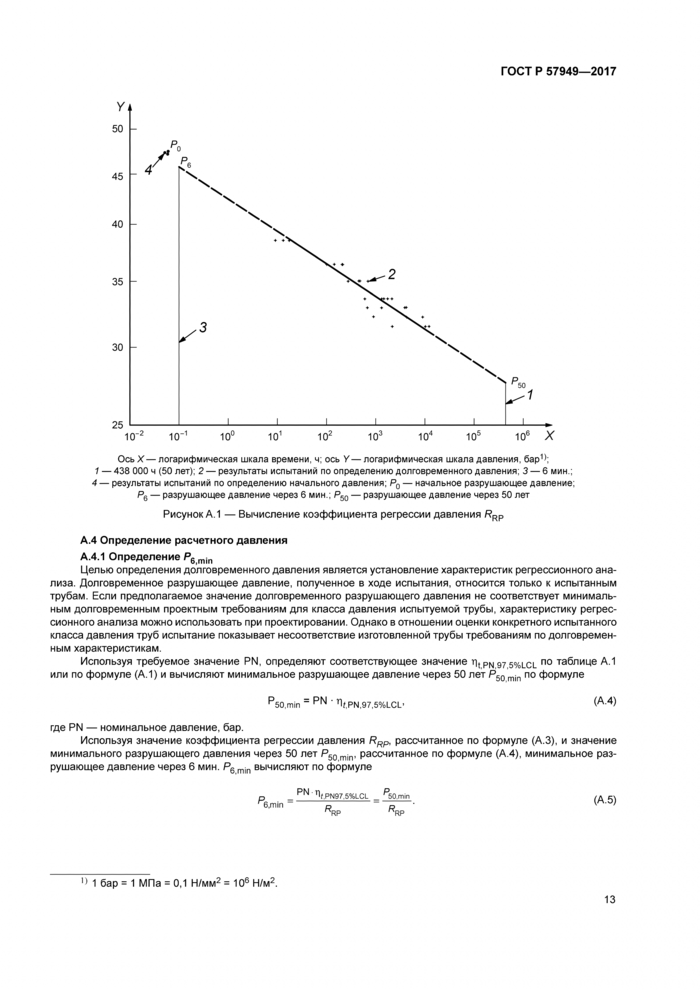
На основе результатов испытаний по определению долговременного давления определяют линию регрессии с использованием метода А настоящего стандарта. По проецируемым точкам линии регрессии в точках 0,1 ч (6 мин.) и 438 000 ч (50 лет) определяют значения разрушающего давления Р6 и Р50 (см. рисунок А.1).
Коэффициент регрессии давления PRP определяют по формуле
Krp=—■ (А.З)
Г6
|
ОсьХ—логарифмическая шкала времени, ч; ось У—логарифмическая шкала давления, бар1); 1 — 438 ООО ч (50 лет); 2 — результаты испытаний по определению долговременного давления; 3 — 6 мин.; 4 — результаты испытаний по определению начального давления; Р0 — начальное разрушающее давление; Р6 — разрушающее давление через 6 мин.; Р50 — разрушающее давление через 50 лет |
Рисунок А. 1 — Вычисление коэффициента регрессии давления PRP
А.4 Определение расчетного давления
А.4.1 Определение Р6 min
Целью определения долговременного давления является установление характеристик регрессионного анализа. Долговременное разрушающее давление, полученное в ходе испытания, относится только к испытанным трубам. Если предполагаемое значение долговременного разрушающего давления не соответствует минимальным долговременным проектным требованиям для класса давления испытуемой трубы, характеристику регрессионного анализа можно использовать при проектировании. Однако в отношении оценки конкретного испытанного класса давления труб испытание показывает несоответствие изготовленной трубы требованиям по долговременным характеристикам.
Используя требуемое значение PN, определяют соответствующее значение 'ntPN 97 5%LCL по таблице А.1 или по формуле (А.1) и вычисляют минимальное разрушающее давление через 50 лет Р50 mjn по формуле
P50,min = PN ‘ Tlf,PNi97i5%LCL» (А4)
где PN — номинальное давление, бар.
Используя значение коэффициента регрессии давления Rrr, рассчитанное по формуле (А.З), и значение минимального разрушающего давления через 50 лет ^50, min’ рассчитанное по формуле (А.4), минимальное разрушающее давление через 6 мин. Р6 mjn вычисляют по формуле
PN • % PN97,5%LCL P50,min
6,min
R,
RP
R,
RP
(A-5)
’) 1 бар = 1 МПа = 0,1 Н/мм2 = 106 Н/м2.
13
А.4.2 Определение расчетного минимального начального разрушающего давления Р0 d
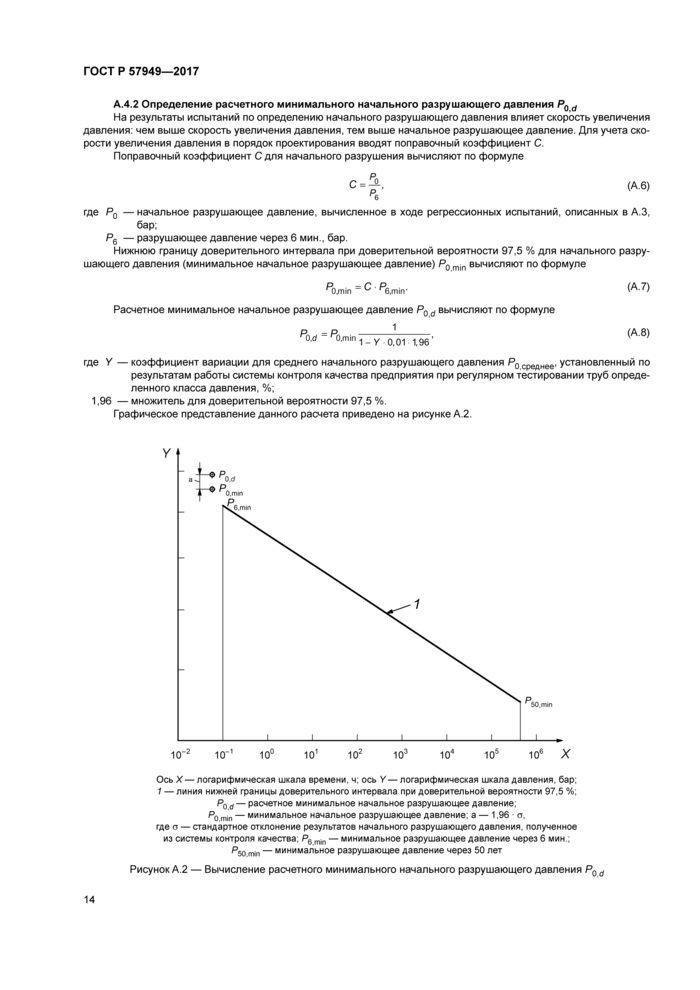
На результаты испытаний по определению начального разрушающего давления влияет скорость увеличения давления: чем выше скорость увеличения давления, тем выше начальное разрушающее давление. Для учета скорости увеличения давления в порядок проектирования вводят поправочный коэффициент С.
Поправочный коэффициент С для начального разрушения вычисляют по формуле
где Р0 — начальное разрушающее давление, вычисленное в ходе регрессионных испытаний, описанных в А.З, бар;
Р6 — разрушающее давление через 6 мин., бар.
(А.7)
Нижнюю границу доверительного интервала при доверительной вероятности 97,5 % для начального разрушающего давления (минимальное начальное разрушающее давление) Р0 mjn вычисляют по формуле
р — р . р #0,min “ ° *6, min*
Расчетное минимальное начальное разрушающее давление Р0 d вычисляют по формуле
(А.8)
р = р _1_
О'd °’min1-y 0,01 1,96 ’
где У — коэффициент вариации для среднего начального разрушающего давления Р0среднее, установленный по результатам работы системы контроля качества предприятия при регулярном тестировании труб определенного класса давления, %;
1,96 — множитель для доверительной вероятности 97,5 %.
Графическое представление данного расчета приведено на рисунке А.2.
|
Ось X—логарифмическая шкала времени, ч; ось У—логарифмическая шкала давления, бар; 1 — линия нижней границы доверительного интервала при доверительной вероятности 97,5 %; P0d — расчетное минимальное начальное разрушающее давление; Р0 mjn — минимальное начальное разрушающее давление; а — 1,96 ■ а, где а — стандартное отклонение результатов начального разрушающего давления, полученное из системы контроля качества; Рб mjn — минимальное разрушающее давление через 6 мин.; Р50 mjn — минимальное разрушающее давление через 50 лет |
Рисунок А.2 — Вычисление расчетного минимального начального разрушающего давления Р0 d
А.5 Порядок контроля PQ d
Чтобы убедиться, что долговременный коэффициент запаса прочности при растяжении, относящийся к 97,5 % LCL через 50 лет r|f PN 97 5o/oLCL и долговременный коэффициент запаса прочности, относящийся к среднему значению минимального разрушающего давления через 50 лет (Р50 среднее min) PN среднее соблюдаются, выполняют следующие расчеты по определению расчетного минимального начального разрушающего давления Р0 d (см. рисунок А.3):
- значение Переднее вычисляют по формуле
Р,\
*6, среднее
- значение ^50, среднее вычисляют по формуле
' о,d . С
(А-9)
Р — р D
*50,среднее *6,среднее rvRP’
- минимальное значение ^50, среднее вычисляют по формуле
р = рм . л
50,среднее,min •f.PN, среднее’
(А. 10)
(А. 11)
где \]t PN СредНее — долговременный коэффициент запаса прочности при растяжении, относящийся к среднему значению минимального разрушающего давления через 50 лет (Р50 среднее min)’ из таблицы А.1 или рассчитанный по формуле (А.2);
- если ^50, среднее’ рассчитанное по формуле (А. 10), больше или равно значению ^50,среднее,min’ рассчитанному по формуле (А.11), то значение Р0 d является достаточным для удовлетворения требований по минимальному значению долговременного коэффициента запаса прочности, относящегося к среднему значению. В противном случае Р0 d необходимо увеличивать, пока данное требование не будет соблюдено. Соблюдение данного требования также обеспечивает удовлетворение требований по минимальному значению долговременного коэффициента запаса прочно
сти при растяжении, относящегося к 97,5 % LCL через 50 лет, так как ^50,
среднее, min
включает в себя значение 1,96 ■ а.
V
10“
Ось X — логарифмическая шкала времени, ч; ось У — логарифмическая шкала давления, бар; 1 — линия нижней границы доверительного интервала при доверительной вероятности 97,5 %; 2 — средняя линия;
3 — PNr|j рм среднее; 4 — PNnf,pNi97i5%LCL; po,d — расчетное минимальное начальное разрушающее давление; Р0 mjn — минимальное начальное разрушающее давление; а — 1,96 ■ о, где о — стандартное отклонение результатов начального разрушающего давления, полученное из системы контроля качества; Р6 mjn — минимальное разрушающее давление через 6 мин.; Р6)Среднее — среднее разрушающее давление через 6 мин.; Р50 mjn — минимальное разрушающее давление через 50 лет; ^50,среднее,min — среднее минимальное разрушающее давление через 50 лет; Р50 среднее — среднее разрушающее давление через 50 лет
|
50,среднее 50,среднее,min | |
|
со | |
|
50,min | ||||
10"1
10°
ю1
10^
10d
ю4
10ь
106 X
Рисунок А.3 — Вычисление долговременных средних значений разрушающего давления
А.6 Оценка характеристик напорных изделий
Используя результаты испытаний начального разрушающего давления, выполненных для определенного класса труб за определенный период времени, вычисляют среднее начальное разрушающее давление Р0 среднее и стандартное отклонение а начального разрушающего давления. Коэффициент вариации для среднего начального разрушающего давления У, %, вычисляют по формуле
У =- 100. (А. 12)
^0, среднее
Для оценки изделия, спроектированного с использованием изложенного метода, система контроля качества должна быть способна подтвердить соответствие изделия требованиям по минимальному давлению, а также установить, является ли среднее начальное разрушающее давление Pq среднее большим или равным расчетному минимальному начальному разрушающему давлению PQ d.
16
ГОСТ P 57949—2017
Содержание
1 Область применения..................................................................1
2 Сущность метода.....................................................................1
3 Методика определения линейных взаимосвязей — методы АиВ.............................1
4 Применение методов регрессионного анализа при испытаниях и проектировании продукции.....10
Приложение А (обязательное) Порядок проектирования напорных труб
и деталей трубопроводов из реактопластов, армированных стекловолокном.......11
Приложение В (справочное) Полиномиальный анализ с использованием взаимосвязей
второго порядка..........................................................17
Приложение С (справочное) Нелинейный метод анализа....................................20
Приложение D (справочное) Расчет нижних границ доверительного и прогнозируемого
интервалов для метода А..................................................36
Приложение ДА (справочное) Оригинальный текст модифицированных структурных
элементов примененного международного стандарта.........................38
Библиография........................................................................39
ГОСТ P 57949—2017
Приложение В (справочное)
Полиномиальный анализ с использованием взаимосвязей второго порядка
В.1 Общие положения
Используя данный метод, строят кривую, задаваемую формулой
у= с+ dx + ex2, (В.1)
где у —десятичный логарифм значения исследуемого свойства; с —точка пересечения с осью У; d, е — коэффициенты двух порядков переменной х; х —десятичный логарифм времени, ч.
В.2 Переменные
Вычисляют следующие переменные:
- —сумму всех отдельно измеренных значений х;
- —сумму квадратов всех отдельно измеренных значений х;
- 'YjXf — сумму кубов всех отдельно измеренных значений х;
- ^xf — сумму четвертых степеней всех отдельно измеренных значений х;
- Ту. —сумму всех отдельно измеренных значений у;
' 2
- (2,у,) — квадрат суммы всех отдельно измеренных значений у;
- 2,у2 —сумму квадратов всех отдельно измеренных значений у
- ^(xj у,) — сумму произведений соответствующих отдельно измеренных значений х(-, у,-;
- J,(x2 у() — сумму произведений соответствующих отдельно измеренных значений xf, у-,
- сумму квадратов остатков, параллельных оси X, Sx для линейного участка, вычисляют по формуле
S, = X(*/-*)2. (В-2)
|
п |
гдеХ— среднеарифметическое значение по всем х(-, вычисляют по формуле (В.З)
- сумму квадратов остатков, параллельных оси X, Sxx для квадратичного участка вычисляют по формуле
sxx = X(x/--*2)2; (В-4)
- сумму квадратов остатков, параллельных оси У, Sy вычисляют по формуле
Sy = I>/-Y)2’ (В-5)
|
п |
где У — среднеарифметическое значение по всем у(-, вычисляют по формуле (В.6)
- сумму квадратов остатков, перпендикулярных кривой, 5худля линейного участка вычисляют по формуле
sxy = X[(x/-*My/-Y)} (в-7)
- сумму квадратов остатков, перпендикулярных кривой, Sxxy для квадратичного участка вычисляют по формуле
(В-8)
Sxxy = X[(x,?-^2)(y,-Y)}
17
Введение
В настоящем стандарте приведены методы регрессионного анализа данных, полученных в ходе испытаний в течение определенного времени, и использование результатов регрессионного анализа при проектировании изделий и оценке их соответствия эксплуатационным требованиям. Для регрессионного анализа используют данные, полученные в ходе испытаний образцов в соответствии с действующими стандартами, устанавливающими методы испытаний для расчета долговременных свойств труб и деталей трубопроводов из реактопластов, армированных стекловолокном, например начального окружного предела прочности при растяжении, долговременной кольцевой деформации, химической стойкости внутренней поверхности в условиях нагружения и долговременной удельной кольцевой жесткости при ползучести или при релаксации.
Был исследован ряд статистических методов, которые можно использовать для регрессионного анализа результатов разрушающих испытаний. Во многих из этих простых методов логарифмы данных должны удовлетворять следующим требованиям:
а) должны иметь нормальное распределение;
б) иметь линию регрессии с отрицательным наклоном;
в) иметь достаточно высокий коэффициент корреляции (см. таблицу 1).
Исследования показали, что требования б) и в) могут быть выполнены, а требование а) — нет, так как в распределении существует асимметрия. Дальнейшие исследования методов, применимых к асимметричным распределениям, привели к принятию ковариационного метода регрессионного анализа таких данных в настоящем стандарте.
Результаты неразрушающих испытаний, например на определение долговременной удельной кольцевой жесткости при ползучести или при релаксации, как правило, удовлетворяют всем трем требованиям, поэтому в соответствии с настоящим стандартом к ним применим более простой метод с использованием времени в качестве независимой переменной.
Данные методы регрессионного анализа данных ограничиваются методами анализа, определенными в стандартах на продукцию или методы испытаний. Для экстраполяции и прогнозирования долговременных свойств труб и деталей трубопроводов из реактопластов, армированных стекловолокном, могут быть использованы другие методы анализа. Например, полиномиальный анализ с использованием взаимосвязей второго порядка допускается применять для экстраполяции данных долговременной удельной кольцевой жесткости при ползучести или при релаксации, особенно при анализе данных за короткий период, когда форма кривых долговременной удельной кольцевой жесткости при ползучести или при релаксации может сильно отличаться от линейной. Полиномиальный анализ с использованием взаимосвязей второго порядка приведен в приложении В. В приложении С приведен альтернативный метод нелинейного анализа. Приложения В и С имеют справочный характер, и нелинейные методы, приведенные в них, применимы только для труб и деталей трубопроводов из реактопластов, армированных стекловолокном, и могут быть не применимы при исследовании других труб.
IV
ГОСТ Р 57949-2017 (ИСО 10928:2009)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТРУБЫ И ДЕТАЛИ ТРУБОПРОВОДОВ ИЗ РЕАКТОПЛАСТОВ, АРМИРОВАННЫХ СТЕКЛОВОЛОКНОМ
Методы регрессионного анализа
Fiberglass-reinforced thermosetting plastics pipes and parts of pipelines. Methods for regression analysis
Дата введения — 2018—06—01
1 Область применения
Настоящий стандарт устанавливает два метода регрессионного анализа данных, которые при преобразовании в логарифмические значения имеют нормальное или асимметричное распределение. Настоящий стандарт применяют совместно со стандартами на методы испытаний труб и деталей трубопроводов из реактопластов, армированных стекловолокном для анализа зависимости их свойств от времени. Настоящий стандарт может быть также применен для анализа других данных.
Порядок проведения испытаний для сбора данных, количество требуемых образцов и период времени сбора данных установлены в стандартах на методы испытаний труб и деталей трубопроводов из реактопластов, армированных стекловолокном.
2 Сущность метода
Регрессионный анализ проводят на основе метода наименьших квадратов, который можно адаптировать к асимметричному и/или нормальному распределениям. Используют два метода регрессионного анализа:
- метод А: ковариационный метод с использованием взаимосвязей первого порядка;
- метод В: метод наименьших квадратов с использованием взаимосвязей первого порядка, где в качестве независимой переменной используют время.
Методы регрессионного анализа включают в себя статистическую проверку корреляции данных и их пригодности к экстраполяции.
Экстраполяция с использованием методов регрессионного анализа позволяет продлить данные, полученные в течение 10 000 ч, для прогнозирования свойств на 50 лет, что, как правило, является максимальным временем экстраполяции.
В разделе 4 приведено применение методов регрессионного анализа при испытаниях и проектировании продукции.
3 Методика определения линейных взаимосвязей — методы А и В
3.1 Общие положения для методов А и В
Используя метод А (см. 3.2) или В (см. 3.3) строят прямую, задаваемую формулой
y=a + bx, (1)
где у —десятичный логарифм значения исследуемого свойства; а — точка пересечения с осью У; b —угол наклона прямой; х —десятичный логарифм времени, ч.
Издание официальное
3.2 Метод А — ковариационный метод
3.2.1 Общие положения
Рассчитывают переменные в соответствии с 3.2.2—3.2.5, используя формулы (2)—(4). Сумму квадратов регрессионных остатков, параллельных оси У, Qy вычисляют по формуле
Q„
m-yf
п
(2)
где у, — отдельное измеренное значение;
У — среднеарифметическое значение по всем у,, вычисляют по формуле (5); п — общее количество результатов (соответствующие пары хр yj).
Сумму квадратов регрессионных остатков, параллельных оси X, Qx вычисляют по формуле
Q
К*,-*)2
п
(3)
где х, — отдельное измеренное значение;
X — среднеарифметическое значение по всем х,, вычисляют по формуле (6).
Сумму квадратов регрессионных остатков, перпендикулярных прямой, Qxy вычисляют по формуле
I [(*,-*)• (у,-г)]
(4)
где
у ХУ/
п
x = Si
(5)
(6)
Примечание — Если значение Qxy больше нуля, угол наклона прямой Ь положительный, если меньше нуля — отрицательный.
3.2.2 Пригодность данных
Квадратичный коэффициент корреляции г2 вычисляют по формуле
|
rz = ——. Q Q |
(7)
Линейный коэффициент корреляции г вычисляют по формуле
(8)
Данные непригодны для анализа, если выполняется неравенство
<Jn-2 + [t(f)f
где t(f) — f-критерий Стьюдента.
В таблице 1 приведены минимальные допустимые значения линейного коэффициента корреляции г в зависимости от количества переменных п. Значения f-критерия Стьюдента основаны на двухстороннем уровне значимости 0,01.
|
Таблица 1 — Минимальные допустимые значения линейного коэффициента корреляции г | ||||||||||||
|
|
Количество переменных, п |
Число степеней свободы, (п-2) |
f-критерий Стьюдента, t (0,01) |
Минимальное значение, г |
|
15 |
13 |
3,012 |
0,6411 |
|
16 |
14 |
2,977 |
0,6226 |
|
17 |
15 |
2,947 |
0,6055 |
|
18 |
16 |
2,921 |
0,5897 |
|
19 |
17 |
2,898 |
0,5751 |
|
20 |
18 |
2,878 |
0,5614 |
|
21 |
19 |
2,861 |
0,5487 |
|
22 |
20 |
2,845 |
0,5368 |
|
23 |
21 |
2,831 |
0,5256 |
|
24 |
22 |
2,819 |
0,5151 |
|
25 |
23 |
2,807 |
0,5052 |
|
26 |
24 |
2,797 |
0,4958 |
|
27 |
25 |
2,787 |
0,4869 |
|
32 |
30 |
2,750 |
0,4487 |
|
37 |
35 |
2,724 |
0,4182 |
|
42 |
40 |
2,704 |
0,3932 |
|
47 |
45 |
2,690 |
0,3721 |
|
52 |
50 |
2,678 |
0,3542 |
|
62 |
60 |
2,660 |
0,3248 |
|
72 |
70 |
2,648 |
0,3017 |
|
82 |
80 |
2,639 |
0,2830 |
|
92 |
90 |
2,632 |
0,2673 |
|
102 |
100 |
2,626 |
0,2540 |
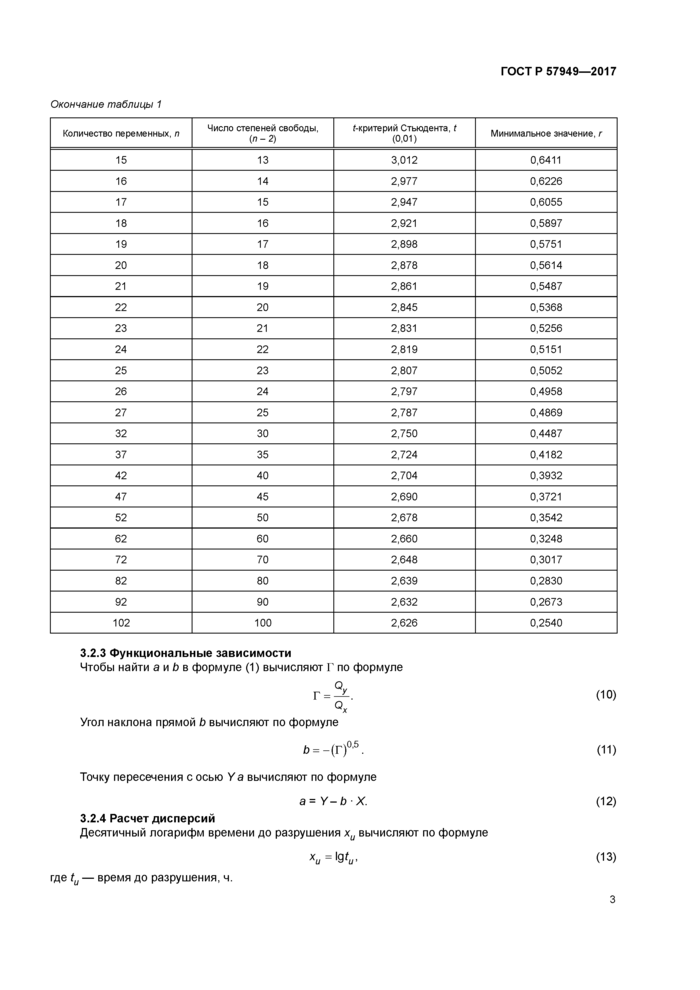
3.2.3 Функциональные зависимости
Чтобы найти а и b в формуле (1) вычисляют Г по формуле
Q
Г = -*-. (Ю)
Q
Угол наклона прямой b вычисляют по формуле
Ь = -( Г)0’5. (11)
Точку пересечения с осью У а вычисляют по формуле
а = Y- b ■ X. (12)
3.2.4 Расчет дисперсий
Десятичный логарифм времени до разрушения хи вычисляют по формуле
xu = Wu, (13)
где tu — время до разрушения, ч.
3
Для каждого отдельно измеренного значения от / = 1 до п вычисляют статистические показатели: - наилучшее значение для истинного значения по формуле
г-*/+ь(У/-а).
2Г
- наилучшее значение для истинного значения у, у/ по формуле
(14)
у/ = а + b ■ х/.
Дисперсию ошибки of для х вычисляют по формуле
(15)
.2 _ 8 “
(л-2).Г
(16)
Переменные Е и D вычисляют по формулам (17) и (18) соответственно:
Е =
2'Qxy’
(17)
D =
2 Г - Ь • о|
л • Q
(18)
ху
Дисперсию угла наклона прямой С вычисляют по формуле
С = D (1 + Е).
(19)
3.2.5 Проверка пригодности к экстраполяции
Если прямую предполагается экстраполировать, вычисляют значение Т по формуле
ь ь
, \0,5 /'"'0,5
varЬ) ^
(20)
Если абсолютное значение Т, то есть |Т|, равно или больше, чем применяемое значение f-критерия Стьюдента tv, приведенное в таблице 2 для степеней свободы (п - 2), данные пригодны для экстраполяции.
Примечание — Расчет границ доверительного интервала не требуется, но в приложении D приведен порядок расчета нижних границ доверительного и прогнозируемого интервалов (LCL и LPL соответственно).
|
Таблица 2 — Значения f-критерия Стьюдента tv (вероятность выхода за границы доверительного интервала 2,5 %, двусторонний уровень значимости 5 %, доверительная вероятность 97,5 %) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Число степеней свободы, (л-2) |
Значения f-критерия Стьюдента, tv |
Число степеней свободы, (п-2) |
Значения f-критерия Стьюдента, tv |
Число степеней свободы, (п-2) |
Значения f-критерия Стьюдента, tv |
Число степеней свободы, (п-2) |
Значения f-критерия Стьюдента, tv |
|
11 |
2,2010 |
36 |
2,0281 |
61 |
1,9996 |
86 |
1,9879 |
|
12 |
2,1788 |
37 |
2,0262 |
62 |
1,9990 |
87 |
1,9876 |
|
13 |
2,1604 |
38 |
2,0244 |
63 |
1,9983 |
88 |
1,9873 |
|
14 |
2,1448 |
39 |
2,0227 |
64 |
1,9977 |
89 |
1,9870 |
|
15 |
2,1315 |
40 |
2,0211 |
65 |
1,9971 |
90 |
1,9867 |
|
16 |
2,1199 |
41 |
2,0195 |
66 |
1,9966 |
91 |
1,9864 |
|
17 |
2,1098 |
42 |
2,0181 |
67 |
1,9960 |
92 |
1,9861 |
|
18 |
2,1009 |
43 |
2,0167 |
68 |
1,9955 |
93 |
1,9858 |
|
19 |
2,0930 |
44 |
2,0154 |
69 |
1,9949 |
94 |
1,9855 |
|
20 |
2,0860 |
45 |
2,0141 |
70 |
1,9944 |
95 |
1,9853 |
|
21 |
2,0796 |
46 |
2,0129 |
71 |
1,9939 |
96 |
1,9850 |
|
22 |
2,0739 |
47 |
2,0112 |
72 |
1,9935 |
97 |
1,9847 |
|
23 |
2,0687 |
48 |
2,0106 |
73 |
1,9930 |
98 |
1,9845 |
|
24 |
2,0639 |
49 |
2,0096 |
74 |
1,9925 |
99 |
1,9842 |
|
25 |
2,0595 |
50 |
2,0086 |
75 |
1,9921 |
100 |
1,9840 |
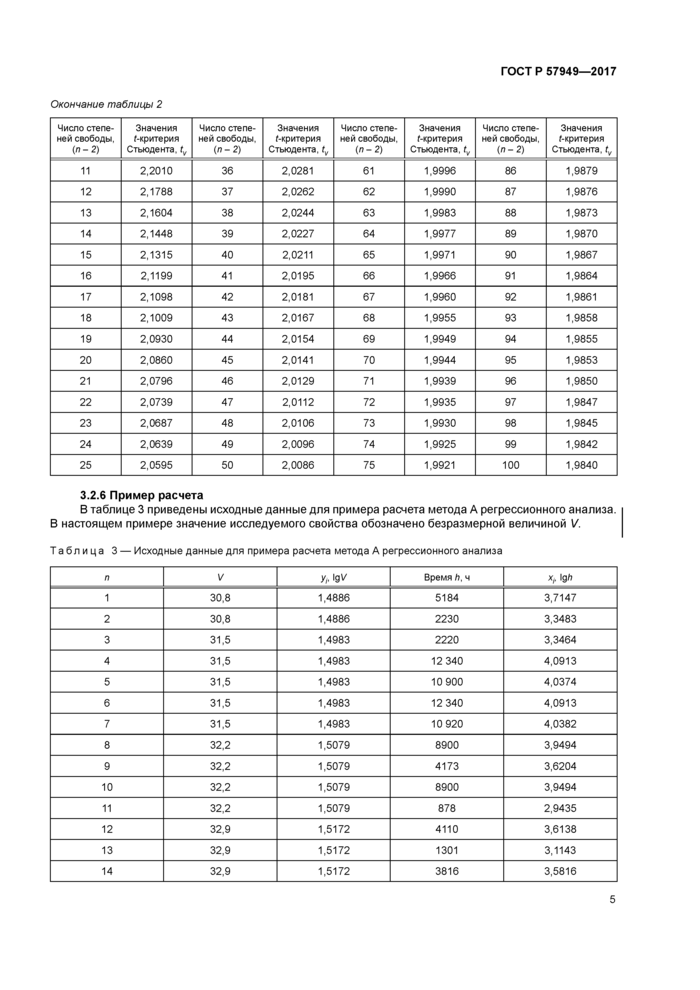
3.2.6 Пример расчета
В таблице 3 приведены исходные данные для примера расчета метода А регрессионного анализа. В настоящем примере значение исследуемого свойства обозначено безразмерной величиной V.
|
Таблица 3 — Исходные данные для примера расчета метода А регрессионного анализа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
п |
У |
У/. W |
Время h, ч |
х(, 1д/> |
|
15 |
32,9 |
1,5172 |
669 |
2,8254 |
|
16 |
33,6 |
1,5263 |
1430 |
3,1553 |
|
17 |
33,6 |
1,5263 |
2103 |
3,3228 |
|
18 |
33,6 |
1,5263 |
589 |
2,7701 |
|
19 |
33,6 |
1,5263 |
1710 |
3,2330 |
|
20 |
33,6 |
1,5263 |
1299 |
3,1136 |
|
21 |
35,0 |
1,5441 |
272 |
2,4346 |
|
22 |
35,0 |
1,5441 |
446 |
2,6493 |
|
23 |
35,0 |
1,5441 |
466 |
2,6684 |
|
24 |
35,0 |
1,5441 |
684 |
2,8351 |
|
25 |
36,4 |
1,5611 |
104 |
2,0170 |
|
26 |
36,4 |
1,5611 |
142 |
2,1523 |
|
27 |
36,4 |
1,5611 |
204 |
2,3096 |
|
28 |
36,4 |
1,5611 |
209 |
2,3201 |
|
29 |
38,5 |
1,5855 |
9 |
0,9542 |
|
30 |
38,5 |
1,5855 |
13 |
1,1139 |
|
31 |
38,5 |
1,5855 |
17 |
1,2304 |
|
32 |
38,5 |
1,5855 |
17 |
1,2304 |
|
Средние: |
У = 1,5301 |
Х = 2,9305 |
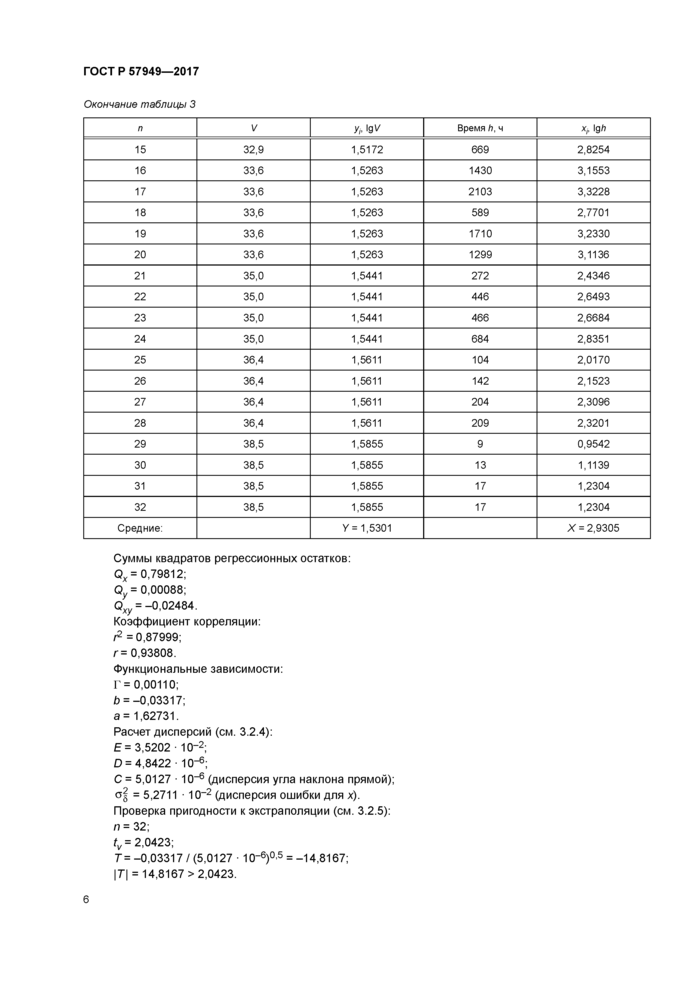
Суммы квадратов регрессионных остатков:
Qx= 0,79812;
Qy= 0,00088;
Qxy = -0,02484.
Коэффициент корреляции: г2 =0,87999; г= 0,93808.
Функциональные зависимости:
Г = 0,00110;
Ь = -0,03317; а= 1,62731.
Расчет дисперсий (см. 3.2.4):
Е= 3,5202 ■ 10-2;
D = 4,8422 ■ 10-1;
С = 5,0127 ■ 10“1 (дисперсия угла наклона прямой); Og = 5,2711 ■ 10“2 (дисперсия ошибки для х). Проверка пригодности к экстраполяции (см. 3.2.5): п = 32; tv= 2,0423;
Т= -0,03317 / (5,0127 ■ Ю"1)0 5 = -14,8167;
|Т| = 14,8167 >2,0423.
1