ГОСТ Р 54500.3-2011
Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения
Купить ГОСТ Р 54500.3-2011 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Руководство устанавливает общие правила оценивания и выражения неопределенности измерения, которые следует соблюдать при измерениях разной точности и в разных областях - от технических измерений на производстве до фундаментальных научных исследований.
Идентичен ISO/IEC Guide 98-3:2008
Оглавление
1 Область применения
2 Термины и определения
3 Основные понятия
4 Оценивание стандартной неопределенности
5 Определение суммарной стандартной неопределенности
6 Определение расширенной неопределенности
7 Представление результатов оценивания неопределенности
8 Краткое описание процедуры оценивания и представления неопределенности
Приложение А (справочное) Рекомендации Рабочей группы по неопределенности и МКМВ
Приложение В (обязательное) Основные метрологические термины
Приложение С (справочное) Основные термины и понятия математической статистики
Приложение D (справочное) Понятия «истинное значение», «погрешность» и «неопределенность»
Приложение Е (справочное) Мотивы и основы для разработки Рекомендации INC-1 (1980)
Приложение F (рекомендуемое) Практические рекомендации по оцениванию составляющих неопределенности
Приложение G (рекомендуемое) Число степеней свободы и уровни доверия
Приложение Н (справочное) Примеры
Приложение J (обязательное) Основные обозначения
Библиография
| Дата введения | 01.10.2012 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Завершение срока действия | 01.09.2018 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Строительство
- Раздел Экология
Организации:
| 16.11.2011 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 555-ст |
|---|---|---|---|
| Разработан | ФГУП ВНИИМ им. Д. И. Менделеева | ||
| Разработан | АНО НИЦ КД | ||
| Издан | Стандартинформ | 2012 г. |
Uncertainty of measurement. Part 3. Guide to the expression of uncertainty in measurement
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20

стр. 21
стр. 22
стр. 23

стр. 24

стр. 25

стр. 26

стр. 27

стр. 28

стр. 29

стр. 30
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ |
ГОСТ Р 54500.3—2011/Руководство ИСО/МЭК 98-3:2008НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЯ
Руководство ИСО/МЭК 98-3:2008НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЯ
Часть 3
Руководство по выражению неопределенности измерения
ISO/IEC Guide 98-3:2008 Uncertainty of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM:1995)
(IDT)
Издание официальное
|
Москва Стандартинформ 2012 |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации — ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева» (ФГУП «ВНИИМ») и Автономной некоммерческой организацией «Научно-исследовательский центр контроля и диагностики технических систем» (АНО «НИЦ КД») на основе собственного аутентичного перевода на русский язык международного документа, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК125 «Статистические методы в управлении качеством продукции»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 16 ноября 2011 г. № 555-ст
4 Настоящий стандарт идентичен международному документу Руководство ИСО/МЭК 98-3:2008 «Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения» [ISO/IEC Guide 98-3:2008 «Uncertainty of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM: 1995)»]
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом указателе «Национальные стандарты», а текст изменений и поправок—в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
©Стандартинформ, 2012
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008
шить, увеличив число наблюдений. Математическое ожидание (ожидаемое значение) (С.2.9, С.3.1) случайной погрешности равно нулю.
Примечание 1 — Выборочное стандартное отклонение среднего арифметического значения ряда наблюдений (см. 4.2.3) не является случайной погрешностью среднего значения, хотя такое толкование встречается в некоторых публикациях. На самом деле эта величина является мерой неопределенности среднего значения, обусловленной случайными эффектами. Точное значение погрешности среднего значения, обусловленной этими эффектами, не может быть известно.
Примечание 2 — В настоящем Руководстве уделяется большое внимание различию терминов «погрешность» и «неопределенность». Эти слова не являются синонимами, отражают разные понятия, и их не следует путать друг с другом или использовать в неправильном значении.
3.2.3 Систематическую погрешность, также как и случайную, нельзя устранить полностью, но зачастую можно уменьшить. Если систематическая погрешность возникает в результате известного действия влияющей величины на результат измерения (далее — систематического эффекта), то это влияние можно количественно оценить и, если оно существенно по сравнению с требуемой точностью измерения, внести поправку (В.2.23) или поправочный коэффициент (В.2.24) для его компенсации. Предполагается, что после внесения поправки математическое ожидание погрешности, обусловленной систематическим эффектом, становится равным нулю.
Примечание - Неопределенность поправки, вносимой в результат измерения для компенсации систематического эффекта, не является систематической погрешностью (часто называемой смещением) результата измерения, связанной с этим эффектом, как ее иногда определяют. На самом деле она представляет собой меру неопределенности результата из-за неполного знания о требуемом значении поправки. Погрешность, появляющаяся от неполной компенсации систематического эффекта, не может быть известна точно. Термины «погрешность» и «неопределенность» следует использовать правильно и следить за тем, чтобы не путать их.
3.2.4 Далее предполагается, что приняты все меры для выявления значимых систематических эффектов и соответствующие поправки внесены в результат измерения.
Пример — В результат измерения падения напряжения (измеряемая величина) на высокоомном резисторе вносят поправку, обусловленную конечным электрическим сопротивлением вольтметра для уменьшения систематического эффекта, вызванного присоединением вольтметра. Для вычисления поправки используют значения сопротивлений вольтметра и резистора, которые получены в результате других измерений и сами содержат неопределенности. Эти неопределенности учитывают при оценивании составляющей неопределенности измерения падения напряжения, связанной с вносимой поправкой и, в конечном счете, с систематическим эффектом вследствие конечного электрического сопротивления вольтметра.
Примечание 1 — Часто с целью исключить систематические эффекты измерительные приборы и системы настраивают или калибруют с использованием эталонов и стандартных образцов, однако при этом следует учитывать составляющие неопределенности, вносимые эталонами и стандартными образцами.
Примечание 2 — Случай, когда поправку на известный значимый систематический эффект не вносят, рассмотрен в примечании к 6.3.1 и в F.2.4.5.
3.3 Неопределенность
3.3.1 Неопределенность результата измерения отражает отсутствие точного знания значения измеряемой величины (см. 2.2). Результат измерения после внесения в него поправки на известные систематические эффекты остается только оценкой значения измеряемой величины, поскольку содержит неопределенности, связанные со случайными эффектами и неточностью поправки результата на систематические эффекты.
Примечание — Может оказаться, что результат измерения (после внесения поправки) будет очень близким к значению измеряемой величины и тем самым иметь пренебрежимо малую погрешность. Эту неисклю-ченную малую систематическую погрешность не следует путать с неопределенностью результата измерения.
3.3.2 Разнообразие источников неопределенности измерений включает в себя:
a) неполное определение измеряемой величины;
b) несовершенную реализацию определения измеряемой величины;
c) нерепрезентативность выборки (измерения проводят на образце, не представляющем измеряемую величину);
d) неточное знание влияния условий окружающей среды на результат измерения или неточное измерение величин, характеризующих эти условия;
5
e) субъективная систематическая погрешность (вносимая оператором при снятии показаний аналоговых приборов);
f) конечную разрешающую способность или порог чувствительности прибора;
д) неточные значения, приписанные эталонам и стандартным образцам;
h) неточные знания физических констант и других параметров, полученных из сторонних источников и используемых при обработке данных;
i) аппроксимации и предположения, используемые в методе и методике измерений (измерительной процедуре);
j) изменчивость в повторных наблюдениях при, казалось бы, неизменных условиях измерений.
Эти источники необязательно являются независимыми, например некоторые из источников, указанных в перечислениях а) — i), могут вносить вклад в источник, указанный в перечислении j). Если какой-либо систематический эффект не был выявлен, то он не может быть учтен в оценке неопределенности результата измерения, хотя и вносит вклад в погрешность измерения.
3.3.3 Рекомендация INC-1 (1980) Рабочей группы по неопределенности разделяет составляющие неопределенности на две категории в зависимости от метода оценивания: по типу А или В (см. 2.3.2 и 2.3.3). Эта классификация применима только к неопределенности и не является заменой классификации погрешности на случайную и систематическую. Неопределенность поправки на известный систематический эффект может в некоторых случаях быть оценена по типу А, а в других случаях — по типу В. То же самое относится к неопределенности, обусловленной случайными эффектами.
Примечание — В ряде публикаций составляющие неопределенности разделяют на «случайные» и «систематические», связывая их с погрешностями, возникающими, соответственно, из случайных и известных систематических эффектов. Такая классификация составляющих неопределенности может привести к неоднозначности толкования при ее практическом применении. Например, «случайная» составляющая неопределенности в одном измерении может стать «систематической» составляющей в другом измерении, в котором результат первого измерения используется в качестве входных данных. При классификации методов оценивания составляющих неопределенности, а не самих составляющих, такая неоднозначность устраняется. В то же время это не мешает объединять отдельные составляющие, оцененные двумя разными методами, в группы для конкретных целей (см. 3.4.3).
3.3.4 Классификация по типам А и В введена только для указания на наличие двух разных способов оценивания составляющих неопределенности и для удобства обсуждения. Ее не следует интерпретировать как различие в природе составляющих неопределенности, полученных разными методами оценивания. Оба способа оценивания основаны на распределении вероятностей (С.2.3), и независимо от способа оценивания составляющие неопределенности количественно характеризуются одним и тем же параметром: дисперсией или стандартным отклонением.
3.3.5 Оценку дисперсии и2 для составляющей неопределенности, оцениваемой по типу А, получают на основе ряда повторных наблюдений, и она совпадает с известной статистической характеристикой — выборочной дисперсией s2. Оценка стандартного отклонения (С.2.12, С.2.21, С.3.3) и, представляющая собой положительный квадратный корень из и2, совпадает таким образом с выборочным стандартным отклонением и - s, и для удобства ее иногда называют стандартной неопределенностью типа А. Оценку дисперсии и2 для составляющей неопределенности, оцениваемой по типу В, получают по имеющейся информации (см. 4.3), а оценку стандартного отклонения и иногда называют стандартной неопределенностью типа В.
Таким образом, стандартную неопределенность типа А рассчитывают по плотности распределения (С.2.5), полученной из распределения частот (С.2.18), а стандартную неопределенность типа В — по предполагаемой плотности распределения, отражающей степень уверенности в появлении того или иного события [часто называемой субъективной вероятностью (С.2.1)]. Оба подхода являются общепринятой интерпретацией понятия вероятности.
Примечание — Оценивание составляющей неопределенности по типу В обычно основывается на всей имеющейся в распоряжении надежной информации (см. 4.3.1).
3.3.6 Стандартную неопределенность результата измерения, полученного из значений ряда других величин, называют суммарной стандартной неопределенностью и обозначают ис. Она является оценкой стандартного отклонения результата измерения, равной положительному квадратному корню из суммарной дисперсии, т.е. суммы дисперсий и ковариаций (С.3.4) всех составляющих неопределенности, и полученной по правилу, названному в настоящем Руководстве законом трансформирования неопределенностей (см. раздел 5).
ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008
3.3.7 Для удовлетворения потребностей в ряде областей промышленности и торговли, а также требований в областях здравоохранения и обеспечения безопасности используют расширенную неопределенность U, получаемую умножением суммарной стандартной неопределенности ис на коэффициент охвата к. Назначением U является построение интервала, охватывающего результат измерения, в пределах которого, как можно ожидать, будет находиться большая часть распределения значений, которые обоснованно могут быть приписаны измеряемой величине. Выбор коэффициента к, обычно принимающего значения от 2 до 3, зависит от вероятности охвата или уровня доверия, соответствующего данному интервалу (см. раздел 6).
Примечание — Вместе со значением расширенной неопределенности U следует всегда указывать коэффициент охвата к. Это позволит восстановить значение стандартной неопределенности измеряемой величины, которая впоследствии может быть использована для расчета суммарной стандартной неопределенности результата измерения другой величины, зависящей от первой.
3.4 Практические аспекты
3.4.1 Если все величины, от которых зависит результат измерения, обладают вариативностью, то их неопределенности могут быть получены посредством статистических процедур. Однако на практике такой подход редко может быть реализован вследствие ограничений на временные и иные ресурсы, поэтому неопределенность результата измерения обычно оценивают, используя математическую модель измерения и закон трансформирования неопределенностей. Это объясняет используемое в данном Руководстве допущение, что измерение можно моделировать математически с точностью, достаточной для обеспечения требуемой точности измерения.
3.4.2 Поскольку математическая модель может быть неполной, для оценивания неопределенности на основе данных наблюдений следует обеспечить диапазоны вариативности влияющих величин, соответствующие тем, что имеют место в практических условиях измерений. Для получения достоверных оценок неопределенности рекомендуется, по возможности, использовать эмпирические математические модели, основанные на долговременных измерениях количественных величин, а также эталоны сравнения и контрольные карты, позволяющие судить, находится л и измерение под статистическим контролем. Если данные наблюдений, включая результаты статистически независимых измерений одной и той же измеряемой величины, свидетельствуют о неполноте модели, то модель должна быть пересмотрена. Использование хорошо спланированных экспериментов позволяет существенно повысить достоверность оценок неопределенности, поэтому планирование эксперимента следует рассматривать как важную часть в технике проведения измерений.
3.4.3 Чтобы оценить правильность работы измерительной системы, часто сравнивают выборочное стандартное отклонение полученных с ее помощью результатов измерений с оценкой стандартного отклонения, полученной суммированием составляющих неопределенности от разных источников. В этом случае необходимо учитывать составляющие неопределенности (независимо от того, как получена их оценка — по типу А или В) только от тех источников, которые обусловливают вариативность измеряемой величины в ходе эксперимента.
Примечани е —Для этих целей все источники неопределенности разбивают на две группы: те, которые обусловливают вариативность измеряемой величины в ходе эксперимента, и те, которые в ходе данного эксперимента на изменения значений измеряемой величины влияния не оказывают.
3.4.4 Если неопределенность поправки на систематический эффект незначительна по сравнению с суммарной стандартной неопределенностью результата измерения, то ее при оценивании неопределенности результата измерения можно не учитывать. Если сама поправка на систематический эффект незначительна по сравнению с суммарной стандартной неопределенностью результата измерения, то допускается не вносить эту поправку в результат измерения.
3.4.5 На практике, особенно в области законодательной метрологии, измерительный прибор часто поверяют сравнением с эталоном, и при этом неопределенности, связанные с эталоном и процедурой сравнения, пренебрежимо малы по сравнению с требуемой точностью поверки. Примером может служить использование эталонов массы при поверке весов. Если составляющими неопределенности вследствие их малости допустимо пренебречь, то разность между показанием прибора и эталоном можно рассматривать как погрешность поверяемого прибора (см. также F.2.4.2).
3.4.6 Иногда результат измерения выражают в единицах эталона, а не в соответствующих единицах Международной системы единиц физических величин (СИ). Т.е., по сути, результат измерения выражают в виде отношения к принятому значению эталона. При этом неопределенность, приписанная результату
7
измерения, может быть существенно меньше неопределенности, которая имела бы место при выражении результата измерения в единицах СИ.
Пример — Прецизионный источник напряжения на диоде Зенера калибруют методом сравнения с эталоном постоянного напряжения на основе эффекта Джозефсона. Для расчета напряжения, создаваемого эталоном, используют значение постоянной Джозефсона, рекомендованное для международного применения МКМВ. Относительная суммарная стандартная неопределенность ис (VS)IVS (см. 5.1.6) калибровки источника на диоде Зенера будет равна 2-10г8, если напряжение источника Vs выражено в относительных единицах через напряжение, создаваемое эталоном, и 4-10г7, если оно выражено в единицах СИ (т.е. в вольтах). Разница в оценках обусловлена дополнительной неопределенностью, связанной с выражением постоянной Джозефсона в единицах СИ.
3.4.7 Ошибки при регистрации или анализе данных могут вносить значительную неизвестную погрешность в результат измерения. Если ошибка велика, то ее можно выявить проверкой данных, но небольшие ошибки могут быть замаскированы случайными изменениями измеряемой величины или даже быть приняты за случайные изменения. Такие ошибки не имеют отношения к неопределенности измерения.
3.4.8 Хотя настоящее Руководство устанавливает общую методологию оценивания неопределенности, его применение требует от пользователя критического мышления, интеллектуальной честности и компетентности. Оценивание неопределенности нельзя рассматривать как типовую задачу, требующую применения стандартных математических процедур. От пользователя требуется детальное знание природы измеряемой величины и процедуры измерения. Поэтому качество оценки неопределенности, приписанной результату измерения, зависит, в конечном счете, от понимания, критического анализа и профессиональной добросовестности всех лиц, принимающих участие в ее получении.
4 Оценивание стандартной неопределенности
Дополнительное руководство преимущественно практического характера по оцениванию составляющих неопределенности приведено в приложении F.
4.1 Моделирование измерения
4.1.1 В большинстве случаев измеряемую величину У не измеряют непосредственно, а определяют через N других величин ХЬХ2 XN посредством функциональной зависимости f:
Y=f(XbX2.....XN). (1)
Примечание 1 — В настоящем Руководстве для упрощения записи один и тот же символ используется для обозначения как физической величины (измеряемой величины), так и случайной величины (см. 4.2.1), представляющей возможные значения этой физической величины. Если указано, что величина X, имеет некоторое распределение вероятностей, то она понимается как случайная переменная. При этом предполагается, что сама физическая величина характеризуется одним единственным значением (см. 1.2 и 3.1.3).
Примечание 2 — Если имеется ряд наблюдений случайной величины, то k-е наблюдение случайной величины X, обозначается X, к. Например, если сопротивление резистора обозначить R, то его к-е наблюдение обозначается Rk.
Примечание 3 — Оценка X, (строго говоря, оценка математического ожидания X,) обозначается х(.
Пример—Если к клеммам терморезистора с линейной зависимостью сопротивления от температуры с температурным коэффициентом а, имеющего при температуре t0 сопротивление R0, приложена разность потенциалов V, то рассеиваемую на данном терморезисторе при температуре t мощность Р (измеряемую величину) рассчитывают по формуле
P = f(V, Ro, a, t) = V2/{R0 [1 +aft-10)]}.
Примечани e — Другим методам измерения P будут соответствовать другие математические модели.
4.1.2 Входные величины Х1, Х2.....XN, от которых зависит выходная величина У, также можно рас
сматривать как измеряемые величины, и они тоже могут зависеть от других величин, включая поправки и поправочные коэффициенты на систематические эффекты, что усложняет вид функциональной зависимости f, которая, таким образом, никогда не может быть в явном виде определена полностью. Кроме того, функциональная зависимость / может быть определена экспериментально или существовать только в виде алгоритма численного расчета. Поэтому в настоящем Руководстве функциональная зависимость f понимается в более широком смысле, а именно, как функция, которая включает в себя все величины, в том числе поправки и поправочные коэффициенты, способные существенно влиять на неопределенность измерения У
8
ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008
Таким образом, если данные показывают, что функциональная зависимость/не моделирует измерение с требуемой точностью, то для устранения неадекватности модели в нее должны быть включены дополнительные входные величины (см. 3.4.2). Включением дополнительной входной величины можно учесть неполноту знаний о явлении, влияющем на измеряемую величину. В примере 4.1.1 дополнительные входные величины могут потребоваться, например, чтобы учесть известную неравномерность распределения температуры по резистору, нелинейную зависимость сопротивления резистора от температуры или зависимость сопротивления от атмосферного давления.
Примечание — В то же время формула (1) может иметь самый простой вид, например, У=Х1 -Х2. Такая модель соответствует, к примеру, сравнению двух определений одной и той же величины X.
4.1.3 Входные величины Х1; Х2, ...,XN могут быть разделены на две группы:
- величины, значения и неопределенности которых определяют непосредственно в текущем измерении. Эти значения и неопределенности можно получить, например, в результате однократного наблюдения, повторных наблюдений или по основанным на опыте суждениям. Они могут включать определения поправок к показаниям приборов и поправок на влияющие величины, такие как окружающая температура, атмосферное давление и влажность;
- величины, значения и неопределенности которых получены из сторонних источников. К ним относятся величины, связанные с аттестованными эталонами, стандартными образцами веществ и материалов, а также величины, значения которых указаны в справочниках.
4.1.4 Оценку измеряемой величины У, обозначаемую у, получают из формулы (1), подставляя в нее входные оценки хь х2, .... xN для N входных величин Хь Х2, .... XN. Таким образом, выходная оценка у, являющаяся результатом измерения, имеет вид
y=f(x i,x2.....xN). (2)
Примечание — В некоторых случаях оценку у получают как среднее арифметическое (см. 4.2.1) п независимых определений Yk величины У по формуле
У = У = 1ХУЛ = 1 tf(xXk, xZk,...,xNM),
k=1 'k=1
когда каждое определение имеет одну и ту же неопределенность и каждое основано на полном наборе наблюдаемых значений N входных величин X/, полученных в одно и то же время. Этому способу усреднения следует отдать
_ _ _ _ . п
предпочтение перед расчетом по формуле у = f(Xv Х2 XN), где X, = — ^Х,- к ~ среднее арифметическое
п к=1
отдельных наблюдений X, к, в тех случаях, когда функциональная зависимость /нелинейна. Для линейной зависимости /указанные два способа усреднения дают одинаковые результаты (см. Н.2 и Н.4).
4.1.5 Оценку стандартного отклонения результата измерения (оценки выходной величины) у в виде суммарной стандартной неопределенности, обозначаемой ис (у), получают из оценок стандартного отклонения результатов измерений (оценок) х, каждой входной величины в виде стандартных неопределенностей, обозначаемых и (х;) (см. 3.3.5 и 3.3.6).
4.1.6 Каждую входную оценку х, и связанную с ней стандартную неопределенность и (х,) получают из вероятностного распределения значений входной величины Хг Это вероятностное распределение можно интерпретировать как частотную вероятность, основанную на серии наблюдений X, к величины Xh или как априорное распределение. Оценки составляющих стандартной неопределенности по типу А основаны на частотном представлении вероятности, а по типу В — на априорных распределениях. Следует понимать, что в обоих случаях распределения отражают некоторое модельное представление знаний о случайной величине.
4.2 Оценивание стандартной неопределенности типа А
4.2.1 В большинстве случаев наилучшей оценкой математического ожидания случайным образом изменяющейся величины q [случайной переменной (С.2.2)], для которой при постоянных условиях измерения (см. В.2.1.5) были получены п независимых наблюдений qk, является среднее арифметическое (или просто среднее) значение q из л наблюдений:
Л п
(3)
'4=1
9
Поэтому для получения результата измерения/по формуле (2) в качестве оценких, входной величины^- по результатам п независимых повторных наблюдений X,к используют среднее арифметическое
значение х, = X,, вычисленное в соответствии с формулой (3). Оценку входных величин, относящихся ко
второй группе по 4.1.3, для которых повторные наблюдения отсутствуют, получают другими методами (см. 4.1.3).
4.2.2 Разброс значений в наблюдениях обусловлен случайными изменениями влияющих величин (случайными эффектами, см. 3.2.2). Выборочную дисперсию s2 (qk), являющуюся оценкой дисперсии а2 для данного распределения вероятностей величины q, получают по формуле
(4)
Положительный квадратный корень s(qk) из выборочной дисперсии называют выборочным стандартным отклонением (см. В.2.17). Эта величина характеризует изменчивость наблюдений qk или, точнее, их
разброс относительно среднего значения q .
4.2.3 Наилучшей оценкой дисперсии среднего значения a2(q), a2 (q)= о2 I п, является
(5)
Выборочная дисперсия среднего значения s2 (q) и выборочное стандартное отклонение среднего значения s(q), равное положительному квадратному корню из s2 (q), определяют количественно, насколько хорошей оценкой математического ожидания \ik величины q является q , и могут быть использованы в качестве меры неопределенности q .
Таким образом, стандартную неопределенность и (xj) оценки х, = X,-, полученную по л независимым повторным наблюдениям X■ к входной величины X,, определяют как ц(х,) = s(X,) с использованием
формулы (5) для оценки s2 (X, ). Для удобства и2 (х, ) = s2 (X, ) и и(х,) = s(X,) иногда называют, соответственно, дисперсией типа А и стандартной неопределенностью типа А.
Примечание 1 — Число наблюдений п должно быть достаточно большим, чтобы q и s2 (q) являлись надежными оценками математического ожидания щ случайной величины q и дисперсии математического ожидания о2 (q)= о2 I п соответственно (см. примечание к 4.3.2). При построении доверительных интервалов
(см. 6.2.2) следует учитывать различие между s2(q) и с2 (q). Если q распределена по нормальному закону (см. 4.3.4), то это различие учитывается применением f-распределения для выборочного среднего (см. G.3.2).
Примечание 2 — Хотя одной из основных характеристик распределения вероятностей является именно
дисперсия, в данном случае s2 (q), на практике удобнее использовать s(q), поскольку эта величина имеет ту же размерность, что и q, и более проста для восприятия, чем дисперсия.
4.2.4 Для измерений, проводимых в хорошо известных условиях под статистическим контролем,
может быть доступна объединенная оценка дисперсии s2 (или объединенное выборочное стандартное
отклонение sp). Если значение измеряемой величины q определяют по п независимым наблюдениям, то в
качестве оценки выборочной дисперсии среднего значения q рекомендуется принимать s2 / п , а не
s2 (qk) / п, а в качестве стандартной неопределенности, соответственно, и = sp / -Jn (см. примечание к
Н.3.6).
4.2.5 Часто для получения оценки х, входной величины X/используют функциональную зависимость, полученную по экспериментальным данным методом наименьших квадратов. Выборочные оценки дисперсий и стандартных отклонений параметров функциональной зависимости, а также значений, прогнозируе-
ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008
мых по данной функциональной зависимости, обычно могут быть легко вычислены с помощью хорошо известных статистических процедур (см. Н.З и [8]).
4.2.6 При заявлении оценки составляющей неопределенности и (х,) типа А всегда необходимо указывать соответствующее ей число степеней свободы v, (С.2.31) — см. G.3. В простейшем случае л независимых наблюдений, когда х, = X, и i/(x,) = s(X,), v, = п - 1.
4.2.7 В случае коррелированной (например, во времени) последовательности наблюдений входной величины среднее значение и выборочное стандартное отклонение, полученные согласно 4.2.1 и 4.2.3, могут быть неадекватными оценками (С.2.25) соответствующих статистик (С.2.23). Для анализа таких наблюдений следует использовать статистические процедуры, специально разработанные для обработки рядов случайных коррелированных результатов измерений.
Примечание — Примером специальных процедур являются те, что используют для обработки результатов измерений эталонов частоты. Может оказаться, что измерения, проявляющие себя как некоррелированные на коротком интервале времени, должны рассматриваться как коррелированные на более длительных интервалах с применением специальных методов обработки (см., например, [9], где подробно рассматривается так называемая дисперсия Аллана).
4.2.8 Анализ оценивания неопределенности типа А в 4.2.1—4.2.7 не является исчерпывающим. Существует много ситуаций, иногда довольно сложных, требующих применения разных статистических методов. Важным примером является планирование эксперимента, часто основанное на применении метода наименьших квадратов, в целях калибровки для оценки неопределенностей, связанных с кратковременными и долговременными случайными изменениями результатов сличений материальных эталонов с неизвестными размерами единиц величин (например, концевых мер длины, эталонов массы) с эталонами сравнения с известными передаваемыми размерами единиц величин. В таких сравнительно простых измерительных задачах составляющие неопределенности часто можно оценить посредством дисперсионного анализа (см. Н.5) результатов иерархических экспериментов для заданного числа уровней иерархии.
Примечание — На низких ступенях поверочной схемы, когда размер единицы величины, передаваемый эталоном сравнения, считают известным точно (поскольку эти эталоны были калиброваны с использованием первичных эталонов), неопределенность результата калибровки может состоять только из стандартной неопределенности типа А, за которую принимают объединенное выборочное стандартное отклонение, полученное в условиях, полно характеризующих измерение.
4.3 Оценивание стандартной неопределенности типа В
4.3.1 Для оценки х, входной величины X,, которая не была определена в результате повторных наблюдений, значения оценки дисперсии и2 (х,) или стандартной неопределенности и (х,) получают в результате обобщения и анализа всей доступной информации о возможной вариативности X,. Такая информация может включать в себя:
-данные предшествующих измерений;
- полученные опытным или теоретическим путем сведения о свойствах материалов и характеристиках приборов;
-характеристики, заявляемые изготовителем;
-данные, приводимые в свидетельствах о калибровке и других документах;
- неопределенности величин, которые вместе со значениями этих величин приведены в справочниках.
Для удобства оценки и2 (х,) и и (х,), полученные таким образом, называют, соответственно, дисперсией типа В и стандартной неопределенностью типа В.
Примечание — Если х, получено из известного априорного распределения вероятностей, то соответствующую этой величине дисперсию следует обозначать и2 (X)- Однако для упрощения в настоящем Руководстве используются обозначения и2 (х;) и и (х/).
4.3.2 Правильное использование доступной информации для оценивания стандартной неопределенности типа В требует физической интуиции, основанной на опыте и общих знаниях, которая приходит с накопленной практикой. Следует понимать, что оценка стандартной неопределенности по типу В может быть не менее надежной, чем оценка стандартной неопределенности по типу А, особенно если последняя получена в условиях небольшого числа статистически независимых наблюдений.
Примечание — Если распределение вероятностей q (см. примечание 1 к 4.2.3) является нормальным, то отношение a[s(q)]la(q) приблизительно равно [2(п -1)]“1/2. Таким образом, если принять o[s(q)] в качестве
11
неопределенности s(q), то для 10 наблюдений (л = 10) относительная неопределенность s(q) будет равна 24 %, а для 50 наблюдений (п = 50) — 10 % (дополнительная информация приведена в таблице Е.1 приложения Е).
4.3.3 Если оценка х, взята из технической документации изготовителя, свидетельства о поверке, справочника или другого документального источника, в котором значение неопределенности х, дано в виде стандартного отклонения, умноженного на некоторый коэффициент, то стандартную неопределенность и(х,) можно получить, разделив справочное значение неопределенности на этот коэффициент, а оценку дисперсии и2(х,) — возведя полученный результат в квадрат.
Пример — Согласно сертификату о калибровке масса ms, эталона из нержавеющей стали с номинальным значением 1 кг равна 1000,000325 г, а его «неопределенность в виде утроенного стандартного отклонения равна 240 мкг». В этом случае стандартную неопределенность эталона массы получают как u(mj = 240/3 = 80 мкг. Это соответствует относительной стандартной неопределенности u(mj/ms = 80-Юг9 (см. 5.1.6). Оценка дисперсии составляет и2(тJ = (80-10-6)2 = 6,4-1<У~9 г2.
Примечание — Как правило, источник информации, указывающий неопределенность измерения какой-либо величины, не приводит составляющие этой неопределенности. В большинстве случаев при выражении неопределенности измерения в соответствии с настоящим Руководством это не имеет значения, поскольку при вычислении суммарной стандартной неопределенности результата измерения единообразно суммируются стандартные неопределенности всех входных величин (см. раздел 5).
4.3.4 Приводимая в том или ином источнике информация о неопределенности х, не всегда имеет вид величины, кратной стандартному отклонению, как рассмотрено в 4.3.3. Часто такую неопределенность определяют в виде интервала с уровнем доверия 90 %, 95 % или 99 % (см. 6.2.2). Если не указано иное, то можно предположить, что для расчета указанного интервала была использована гипотеза о нормальном распределении (С.2.14) величины х(. В этом случае стандартную неопределенность для х, получают делением приведенного в источнике информации значения на соответствующий коэффициент для нормального распределения. Так вышеуказанным трем уровням доверия соответствуют следующие коэффициенты: 1,64; 1,96 и 2,58 (см. также таблицу G.1 приложения G).
Примечание — В таком предположении не было бы необходимости, если бы неопределенность была выражена в соответствии с рекомендациями настоящего Руководства, в котором подчеркивается необходимость при заявлении неопределенности всегда указывать используемый коэффициент охвата (см. 7.2.3).
Пример—Согласно свидетельству о калибровке, сопротивление Rs эталонного резистора с номинальным значением 10 Ом равно 10,000742 Ом ± 129 мкОм при температуре 23 °С и «неопределенность 129 мкОМ соответствует интервалу с уровнем доверия 99 %». В этом случае стандартную неопределенность сопротивления можно принять равной и (Rs) = 129/2,58 = 50 мкОм. Это соответствует относительной стандартной неопределенности и (Rs) / Rs = 5,0-10~6 (см. 5.1.6). Оценка дисперсии равна и2 (Rs) = (5,0-1 (Г6)2 = 2,5-10г9 Ом2.
4.3.5 Рассмотрим случай, когда на основе некоторого источника информации можно сделать заключение, что значение входной величины X) с равной вероятностью может находиться как в пределах интервала от а_ до а+, таки вне этого интервала. Другими словами, вероятность того, что значениеХ, находится в интервале от а_ до а+ равно 0,5 или 50 %. Если есть основания предположить, что распределение вероятностей X, близко к нормальному, то лучшей оценкой х,- для убудет средняя точка этого интервала. Обозначив а полуширину интервала, а = (а+ -а_)/2, можно принять i/(x,) = 1,48а, поскольку для нормального распределения с математическим ожиданием д и стандартным отклонением о интервал д ± о/1,48 охватывает приблизительно 50 % распределения.
Пример — Станочник, определяя размеры детали, решил, что ее длина I с вероятностью 0,5 находится в интервале от 10,07 до 10,15 мм и записал это в виде I = (10,11 ± 0,04) мм, понимая под этим, что ± 0,04 — интервал с уровнем доверия 50 %. В этом случае а = 0,04 мм, и в предположении нормального распределения возможных значений I стандартная неопределенность длины будет равна и (1) = 1,48-0,04 = 0,06 мм. Оценка дисперсии будет и2 (1) = (1,48-0,04)2 = 3,5-10~3 мм2.
4.3.6 Рассмотрим случай, подобный изложенному в 4.3.5, но когда на основе имеющейся информации можно утверждать, что «в двух случаях из трех значение Х; будет находиться в интервале от а_ до а+. Другими словами, вероятность того, что значение X) находится в интервале от а_ до а+ равно приблизительно 0,67. Тогда с достаточным основанием можно принять и(х) = а, поскольку для нормального распределения с математическим ожиданием д и стандартным отклонением о интервал д ± о охватывает приблизительно 68,3 % распределения.
12
ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008
Примечани е — Точное значение стандартного отклонения о, соответствующего интервалу с доверительной вероятностью р = 2/3, равно 0,96742, тогда стандартную неопределенность и (х,-) следовало бы получить по формуле и (Xj) = а/0,96742 = 1,033э. Однако столь высокая точность вычислений стандартной неопределенности, очевидно, не является оправданной.
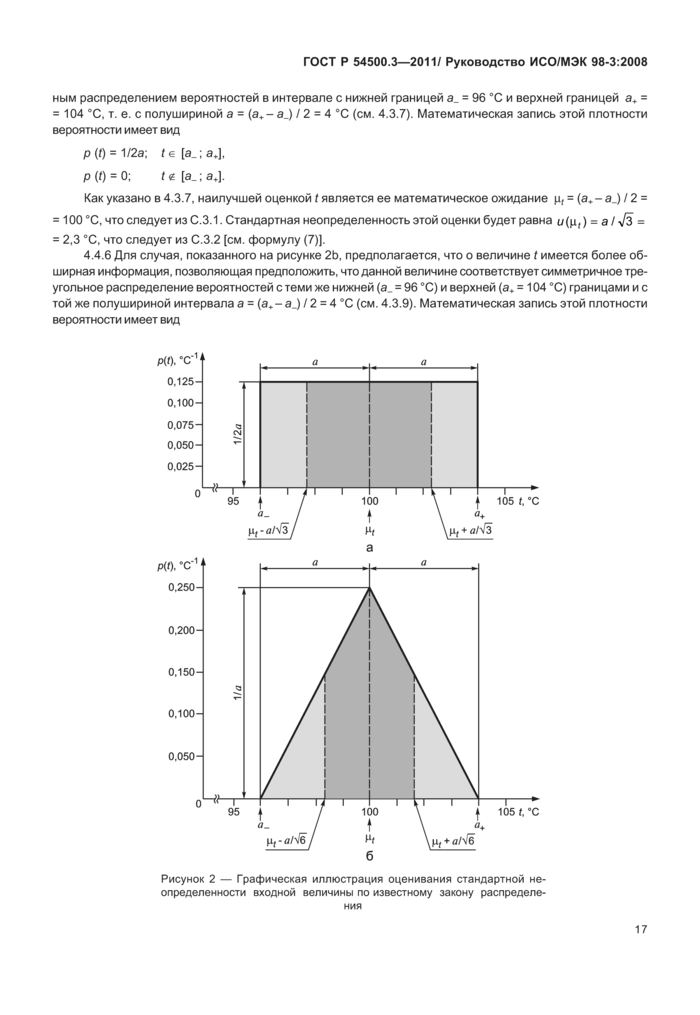
4.3.7 В ряде случаев можно оценить только границы (верхний и нижний пределы) для X), в частности, утверждать, что «для всех практических целей вероятность нахождения значения Xj в интервале от а_ до а+ близка к единице, а вне пределов этого интервала — несущественна». Если дополнительная информация о возможных значениях X, внутри указанного интервала отсутствует, то остается предположить, что вероятность для X, принять любое значение в пределах интервала одинакова (что соответствует равномерному или прямоугольному распределению вероятностей, см. 4.4.5 и рисунок 2). Тогда х„ равное математическому ожиданию Xj, будет средней точкой интервала, х, = (а+ + а_)/2. Дисперсию и2(х,) такого распределения определяют по формуле
(6)
и2(х,) = (а+ - а_)2/12 .
Если разность между границами, а+-а_, обозначить 2а, то формула (6) примет вид
(7)
u2(Xj) - а2/3.
Примечание — Если составляющая неопределенности, полученная таким образом, дает значительный вклад в неопределенность результата измерения, то целесообразно рассмотреть возможность получения дополнительной информации для уточнения вида распределения.
Пример 1 — Согласно справочнику значение температурного коэффициента линейного расширения чистой меди при 20 °С сс20 (Си) равно 16,52-10~6 °С~1, а погрешность этого значения не превышает 0,40- КГ6 °С~1. На основании такой ограниченной информации можно только предположить, что значение а2о (Си) равновероятно распределено в интервале от 16,12-10~6 до 16,92-10~6 °С~* и что вероятность нахождения а2о (Си) вне пределов этого интервала очень мала. Дисперсию симметричного прямоугольного распределения возможных значений о^о (Си) с полушириной а = 0,40-10~6 °С~* можно получить по формуле (7): и2 (а20) = (0,40-1(Г6)2/3 = 53,3-10~15 °С~2. Тогда стандартная неопределенность будет равна
и (а20) = (0,40-1Or6) /4з = 0,23-КГ6 °С~1.
Пример 2 — В технических условиях изготовителем цифрового вольтметра указано, что «в промежутке от года до двух лет после калибровки прибора его погрешность состоит из относительной погрешности, равной 14-КГ6, и погрешности, приведенной к пределу измерений (1 В), равной 2-КГ6. Пусть спустя 20 месяцев после калибровки повторные измерения напряжения V в диапазоне до 1В дали среднее
значение V =0,928571 В. При этом известно, что стандартная неопределенность по типу А, связанная
с изменчивостью при повторных наблюдениях, u(V) =12мкВ. Оценку стандартной неопределенности по типу В по техническим условиям изготовителя можно получить в предположении, что указанная им погрешность определяет симметричные границы равномерного распределения аддитивной поправки AV к V с нулевым математическим ожиданием. Тогда полуширину а диапазона возможных значений A(V) определяют как а = (14-10г6) 0,928571 + (2-КГ6) -1 = 15-10г6 В или 15 мкВ, и из формулы (7) получают u2(AV) = 75 мкВ2 и u(AV) = 8,7 мкВ. Оценка значения измеряемой величины V, для простоты
обозначаемая тем же символом V, равна V = V + AV = 0,928571 В. Суммарную стандартную неопределенность этой оценки получают суммированием стандартной неопределенности по типу А, равной 12 мкВ, и стандартной неопределенности по типу В, равной 8,7 мкВ. Общий метод суммирования составляющих стандартной неопределенности дан в разделе 5, а этот конкретный пример рассмотрен в 5.1.5.
4.3.8 В рассмотренном в 4.3.7 случае верхняя (а+) и нижняя (а_) границы диапазона изменений входной величины Xj могут быть расположены несимметрично относительно лучшей оценки х,-. Так, если нижнюю границу представить в виде а_ = х,-Ь_, а верхнюю — в виде а+ = х,+ Ь+, то может быть справедливо условие Ь_^Ь+. Поскольку в этом случае х,- (математическое ожиданиеX) не находится посередине интервала от а_ до а+, то распределение вероятностей X) не может быть равномерным в данном интервале. При этом имеющейся информации может быть недостаточно, чтобы сделать обоснованное заключение о виде распределения, а произвольный выбор разных моделей распределения даст разные оценки дисперсии. В этом случае простейшей оценкой дисперсии является
(8)
13
которая совпадает с дисперсией прямоугольного распределения в интервале шириной (Ь+ + Ь_) (асимметричные распределения рассматриваются также в F.2.4.4 и G.5.3).
Пример — Пусть в примере 1 ( 4.3.7) в справочнике значение коэффициента дано как о^о (Си) = = 16,52-10г6 °С~1 и указано, что «наименьшее возможное значение коэффициента равно 16,40-10~6 °С~1, а наибольшее — 16,92-10~6 °С~1». Тогда Ь_ = 0,12-10~6 °С~1, Ь+ = 0,40-10~6 °С~1, и по формуле (8) получаем и (О2о) = 0,15-10~6 'С-1.
Примечание 1 — Во многих практических измерительных ситуациях, когда границы асимметричны, целесообразно вносить поправку в оценку х,- на величину (Ь+ - Ь_) / 2, чтобы новая оценка х) величины X/ находилась посередине диапазона, х] = (з+ + э_) / 2. Это сведет ситуацию к случаю, рассмотренному в 4.3.7, при новых значениях Ь'+ = Ь1 = (Ь+ + Ь_) / 2 = (а+ - а_) 12 = а.
Примечание2 — Основываясь на принципе максимума энтропии, можно показать, что в случае асимметричных границ плотность вероятности распределения с максимальной энтропией имеет вид р(Х/) = = А ехр {- л(Х, - X/)}, где А и X являются решением системы уравнений: А = [Ь_ ехр (ХЬ_) + Ь+ ехр (-ХЬ+)]-1, X = = {ехр [Я,(Ь+ + Ь_)]-1 }/{Ь_ ехр [л(Ь+ + Ь_)] + Ь+}\ X > 0 в случае Ь+> Ь_ и X < 0 в случае Ь+ < Ь_. Дисперсия такого распределения имеет вид и2(х() = Ь+Ь_ - (Ь+ - Ь_) / X.
4.3.9 В случае, рассмотренном в 4.3.7, отсутствие информации о возможных значениях величины X, в пределах границ ее изменения от а_ до а+ не позволило сделать иного предположения о плотности распределения вероятностей X,, кроме как принять ее постоянной в пределах интервала от а_ до а+ и нулевой вне этого интервала. Распределение вероятностей такого вида содержит разрывы (на границах интервала), что зачастую не имеет под собой ясной физической основы. Во многих случаях можно ожидать, что значениях, вблизи границ интервала гораздо менее вероятны, чем в его центре. Тогда симметричное прямоугольное распределение целесообразно заменить симметричным трапецеидальным распределением с шириной нижнего основания а+ - а_ = 2а и шириной верхнего основания 2ар, где 0 < р < 1. При Р -> 1 это распределение стремится к прямоугольному, рассмотренному в 4.3.7, а при р -»0 — к треугольному (см. 4.4.6 и рисунок2Ь). Математическое ожидание величины Х/Дпя такого трапецеидального распределения будет равно х, = (а_+ а+) / 2, дисперсия и2 (ху) определяется по формуле
и2 (Ху) = а2 (1 + р2)/6, (9а)
а в случае треугольного распределения (Р = 0):
и2 (ху) = а2/6. (9Ь)
Примечание 1 — Для нормального распределения с математическим ожиданием ц и стандартным отклонением о в интервал ц ± Зо попадают приблизительно 99,73 % значений случайной величины. Таким образом, если принять что интервал от а_ до а+ охватывает не 100 %, а 99,73 % значений и что случайная величина распределена по закону, близкому к нормальному (это будет дополнительной информацией о распределении случайной величины по сравнению с той, что рассмотрена в 4.3.7), то и2 (х,) = а2/9. Для сравнения: дисперсия симметричного прямоугольного распределения на интервале полушириной а равна а2/3 [формула (7)], а дисперсия симметричного треугольного распределения на интервале полушириной а равна а2/6 [формула (9Ь)]. Различия в значениях дисперсий этих трех распределений довольно незначительны по сравнению с разницей в объемах информации, требуемой для обоснования выбора того или иного распределения.
Примечание 2 — Т рапецеидальное распределение можно рассматривать как свертку двух прямоугольных распределений (см. [10]): одного с полушириной а-], равной длине средней линии трапеции, а-| = а (1 + |3)/2, другого — с полушириной а2, равной длине средней линии треугольника, образованного боковой линией, опущенной из нее высотой и частью нижнего основания трапеции, а2 = а (1 - Р)/2. Тогда дисперсию трапецеидального распределения и2 можно представить в виде суммы дисперсий этих двух прямоугольных распределений: и2 = а2/3+а2/3. Свертку распределений можно интерпретировать также как случайную величину, распределенную по равномерному закону на интервале 2а-|, значение которого известно с некоторой неопределенностью, определяемой другим равномерным распределением на интервале 2а2, т. е. как равномерно распределенную случайную величину, границы распределения которой точно не известны. Но даже если з2 составляет 30 % аЛ, стандартное отклонение трапецеидального распределения и будет превышать I >/з менее чем на 5 %.
4.3.10 Важно, чтобы одни и те же составляющие неопределенности не были учтены более одного раза. Если составляющая неопределенности, обусловленная конкретным эффектом, получена оцени-
14
ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008
Содержание
1 Область применения........................................ 1
2 Термины и определения...................................... 2
3 Основные понятия......................................... 3
4 Оценивание стандартной неопределенности............................ 8
5 Определение суммарной стандартной неопределенности...................... 18
6 Определение расширенной неопределенности........................... 22
7 Представление результатов оценивания неопределенности..................... 24
8 Краткое описание процедуры оценивания и представления неопределенности........... 26
Приложение А (справочное) Рекомендации Рабочей группы по неопределенности и МКМВ..... 28
Приложение В (обязательное) Основные метрологические термины................. 30
Приложение С (справочное) Основные термины и понятия математической статистики........ 36
Приложение D (справочное) Понятия «истинное значение», «погрешность» и «неопределенность» . . 43
Приложение Е (справочное) Мотивы и основы для разработки Рекомендации INC-1 (1980)...... 48
Приложение F (рекомендуемое) Практические рекомендации по оцениванию составляющих неопределенности ...................................... 54
Приложение G (рекомендуемое) Число степеней свободы и уровни доверия............. 63
Приложение Н (справочное) Примеры................................ 71
Приложение J (обязательное) Основные обозначения........................ 95
Библиография............................................ 99
ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008
ванием типа В, то она должна войти как независимая составляющая при расчете суммарной стандартной неопределенности только в той части, в какой этот эффект не вызывает вариативности результатов измерения. Это обусловлено тем, что та часть эффекта, которая вносит вклад в вариативность, уже включена в составляющую неопределенности, полученную на основе статистического анализа наблюдений.
4.3.11 Обсуждение оценивания стандартной неопределенности типа В в 4.3.3—4.3.9 проведено на качественном уровне. Однако получение оценок неопределенности в максимально возможной мере должно быть основано на количественных данных, как подчеркивается в 3.4.1 и 3.4.2.
4.4 Графическая иллюстрация оценивания стандартной неопределенности
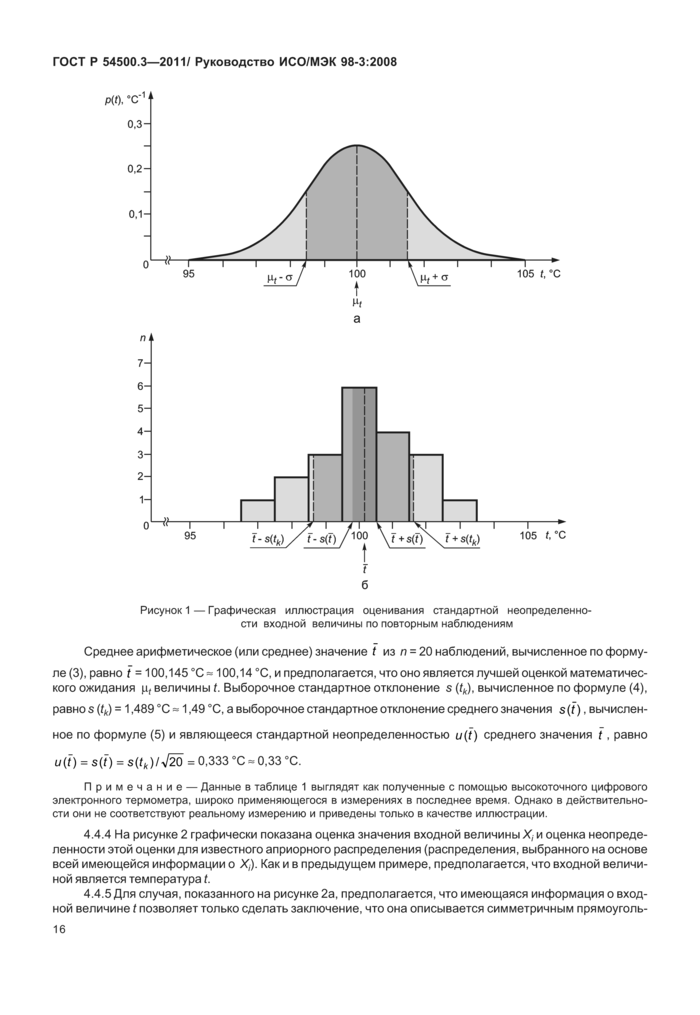
4.4.1 На рисунке 1 графически показана оценка значения входной величины X, и оценка неопределенности этой оценки по выборке (повторным наблюдениям) из генеральной совокупности с неизвестным законом распределения.
4.4.2 На рисунке 1а показан пример, когда входной величиной X/является температура /, а неизвестным распределением является нормальное распределение с математическим ожиданием д* = 100 °С и стандартным отклонением а = 1,5 °С, плотность вероятности которого описывается формулой (см. С.2.14)
Примечание — Из определения плотности распределения вероятностей р (z) следует необходимость выполнения условия jp(z)dz = 1.
4.4.3 На рисунке 1Ь показана гистограмма п = 20 повторных наблюдений tk температуры f, взятых, предположительно, из генеральной совокупности, которая описывается распределением, изображенным на рисунке 1а. Для построения гистограммы наблюдения, значения которых даны в таблице 1, были сгруппированы в классы шириной 1 °С. (Гистограмма приведена в качестве иллюстрации; ее построение не входит в статистический анализ данных.)
|
Таблица 1 —Двадцать повторных наблюдений температуры /, сгруппированных в классы шириной 1 °С | ||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||
|
15 | ||||||||||||||||||||||||||||||||||||||
Аннотация к Руководству ИСО/МЭК 98-3:2008
Руководство устанавливает общие правила оценивания и представления неопределенности измерения применительно к широкому спектру измерений. Основой Руководства является Рекомендация 1 (СИ 981) Международного комитета мер и весов (МКМВ) и Рекомендация INC-1 (1980) Рабочей группы по неопределенности. Рабочая группа по неопределенности была организована Международным бюро мер и весов (МБМВ) по поручению МКМВ. Рекомендация, разработанная Рабочей группой, является единственной рекомендацией в отношении выражения неопределенности измерения, одобренной межправительственной организацией.
Руководство разработано объединенной рабочей группой экспертов, назначенных МБМВ, ИСО, МЭК и МОЗМ.
Следующие семь организаций1 поддержали разработку Руководства, которое публикуется от их имени:
- Международное бюро мер и весов (МБМВ);
- Международная электротехническая комиссия (МЭК);
- Международная федерация клинической химии (МФКХ)2;
- Международная организация по стандартизации (ИСО);
- Международный союз теоретической и прикладной химии (ИЮПАК)2;
- Международный союз теоретической и прикладной физики (ИЮПАП)2;
- Международная организация законодательной метрологии (МОЗМ).
Пользователей Руководства приглашают присылать свои замечания и предложения в любую из семи указанных международных организаций, чьи адреса указаны на обратной странице обложки3.
ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008
Предисловие к Руководству ИСО/МЭК 98-3:2008
В 1978 г., признавая отсутствие международного единства по вопросу выражения неопределенности измерения, наиболее авторитетная международная организация в области метрологии МКМВ обратилась в МБМВ с просьбой рассмотреть эту проблему совместно с национальными метрологическими лабораториями и подготовить соответствующую рекомендацию.
МБМВ подготовило подробную анкету и разослало ее в 32 национальные метрологические лаборатории, заинтересованные в разрешении данной проблемы, а также, для сведения, в пять международных организаций. К началу 1979 г. были получены ответы из21 лаборатории [1]. Почти в каждом ответе подчеркивалась важность установления признанной на международном уровне процедуры выражения неопределенности измерения и объединения частных составляющих неопределенности в одну общую неопределенность. Однако в том, какой должна быть эта процедура, единства достигнуто не было. Для решения этого вопроса МБМВ организовало встречу, на которой присутствовали представители 11 национальных метрологических лабораторий. Эта Рабочая группа по неопределенности разработала Рекомендацию INC-1 (1980) «Выражение экспериментальных неопределенностей» [2]. Рекомендация была одобрена МКМВ в 1981 г. [3] и подтверждена в 1986 г. [4].
Задачу разработки подробного Руководства, основанного на подготовленной Рабочей группой Рекомендации (которая является, скорее, краткой формулировкой общих принципов, чем детализированной инструкцией), МКМВ передал Международной организации по стандартизации ИСО, которая могла в большей степени учесть потребности, возникающие из широких интересов промышленности и торговли.
Ответственность за решение указанной задачи была возложена на Техническую консультативную группу по метрологии (ИСО/ТАГ 4), целью которой, в том числе, является координация разработки руководств в области измерений, представляющих общий интерес для ИСО и других шести организаций, которые вместе с ИСО участвуют в работе ИСОЯАГ 4: МЭК (партнера ИСО в области международной стандартизации); МКМВ и МОЗМ (двух всемирно признанных международных организаций в области метрологии); ИЮПАК и ИЮПАП (двух международных союзов в области физики и химии) и МФКХ.
ИСОЯАГ 4, в свою очередь, учредила Рабочую группу 3 (ИСОЯАГ 4/РГ 3), состоящую из экспертов, предложенных МБМВ, МЭК, ИСО и МОЗМ и утвержденных председателем ИСОЯАГ 4. Перед ней была поставлена следующая задача: разработать руководящий документ, базирующийся на Рекомендации Рабочей группы по неопределенности МБМВ, в котором были бы сформулированы правила выражения неопределенности измерения и который использовался бы организациями и службами в области стандартизации, калибровки, аккредитации лабораторий, а также в метрологии.
Целью данного руководства должно было стать:
- обеспечение предоставления полной информации о том, как получены утверждения о неопределенности измерений;
- создание основы для международного сопоставления результатов измерений.
Настоящее первое издание Руководства ИСО/МЭК 98-3 отменяет и заменяет «Руководство по выражению неопределенности измерений», опубликованное совместно МБМВ, МЭК, МФКХ, ИСО, ИЮПАК, ИЮПАП и МОЗМ в 1993 г. и переизданное с исправлениями в 1995 г*
* Примечание к изданию 2008 г.: При разработке издания 2008 г. в версию 1995 г. были внесены необходимые исправления, подготовленные JCGM/WG 1. Эти исправления затрагивают пункты 4.2.2, 4.2.4, 5.1.2, В.2.17, С.3.2, С.3.4, Е.4.3, Н.4.3, Н.5.2.5 и Н.6.2.
V
Введение
0.1 Сообщению о результате измерения физической величины должна сопутствовать некоторая количественная характеристика качества результата измерений, чтобы при использовании данного результата возможно было оценить его достоверность. Без такой информации результаты измерений нельзя сопоставить ни друг с другом, ни со значениями, указанными в технических условиях или стандарте. Это требует наличия простой в применении, понятной и общепризнанной процедуры, позволяющей характеризовать качество результата измерений, т.е. оценивать и выражать его неопределенность.
0.2 Понятие неопределенности как количественной характеристики является относительно новым в истории измерений, хотя понятия погрешности и анализа погрешностей давно используются в метрологической практике. В настоящее время общепризнанно, что после того, как найдены оценки всех ожидаемых составляющих погрешности и в результат измерения внесены соответствующие поправки, все еще остается некоторая неопределенность в отношении полученного результата, т.е. сомнение в том, насколько точно он соответствует значению измеряемой величины.
0.3 Подобно тому, как Международная система единиц (СИ), будучи системой практически универсального использования, привнесла согласованность во все научные и технические измерения, международное единство в оценивании и выражении неопределенности измерения обеспечило бы должное понимание и правильное использование широкого спектра результатов измерений в науке, технике, торговле, промышленности и законодательстве. В условиях международного рынка чрезвычайно важно, чтобы метод оценивания и выражения неопределенности был единым во всем мире, а результаты измерений, проведенных в разных странах, были легко сопоставимы между собой.
0.4 Идеальный метод оценивания и выражения неопределенности результата измерения должен быть
-универсальным, т.е. применимым ко всем видам измерений и всем видам входной информации, используемой в измерениях.
Величина, непосредственно используемая для выражения неопределенности, должна быть:
- внутренне согласованной, т.е. непосредственно выводиться из составляющих ее компонентов и не зависеть от того, как эти компоненты группируются и как они делятся на подкомпоненты;
-переносимой, т.е. допускающей непосредственное использование неопределенности, полученной для одного результата измерения, в качестве составляющей неопределенности другого измерения, в котором используется первый результат.
Кроме того, зачастую в промышленности и торговле, а также в здравоохранении и в сфере обеспечения безопасности результат измерения должен быть представлен с указанием охватывающего его интервала, в пределах которого, как можно ожидать, будет находиться большая часть распределения значений, которые обоснованно могут быть приписаны измеряемой величине. Таким образом, идеальный метод оценивания и выражения неопределенности измерения должен предоставлять возможность указать такой интервал, в частности, который был бы действительно близок к доверительному интервалу с заданным уровнем доверия.
0.5 Подход, на котором базируется настоящий руководящий документ, изложен в Рекомендации INC-1 (1980) [2] Рабочей группы по неопределенности, организованной МБМВ по инициативе МКМВ (см. предисловие). Данный подход, обоснованность которого обсуждается в приложении Е, соответствует всем вышеуказанным требованиям. Этого нельзя сказать о большинстве других используемых в настоящее время методах. Рекомендация INC-1 (1980) была одобрена и вновь подтверждена МКМВ его собственными Рекомендацией 1 (СИ981) [3] и Рекомендацией 1 (СИ 986) [4], перевод которых приведен в приложении А (разделы А.2 и А.З соответственно). Поскольку основой для настоящего Руководства остается Рекомендация INC-1 (1980), ее перевод также приведен в приложении А (раздел А. 1)4.
0.6 Краткое описание метода, установленного настоящим руководящим документом по оцениванию и выражению неопределенности измерений, приведено в разделе 8, а ряд подробных поясняющих примеров — в приложении Н. Остальные приложения посвящены: терминам, используемым в метрологии (приложение В), основным терминам и понятиям математической статистики (приложение С), сопоставлению понятий «истинное значение», «погрешность» и «неопределенность» (приложение D), практическому руководству по оцениванию составляющих неопределенности (приложение F), оцениванию степеней свободы и уровней доверия (приложение G), используемым основным математическим символам (приложение J). В конце документа приведена библиография.
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЯ Часть 3
Руководство по выражению неопределенности измерения
Uncertainty of measurement. Part 3. Guide to the expression of uncertainty in measurement
Дата введения 2012 — 10—01
1 Область применения
1.1 Настоящее Руководство устанавливает общие правила оценивания и выражения неопределенности измерения, которые следует соблюдать при измерениях разной точности и в разных областях — от технических измерений на производстве до фундаментальных научных исследований. Подход, установленный настоящим Руководством, распространяется на широкий спектр измерений, включая те, что используют для:
- обеспечения требуемого качества продукции и контроля качества на производстве:
- проверки выполнения требований законов и нормативных документов;
- проведения фундаментальных и прикладных исследований и разработок в науке и технике;
- калибровки эталонов и приборов, а также проведения испытаний в соответствии с национальной схемой обеспечения единства измерений (для обеспечения прослеживаемости к национальным эталонам);
- разработки, поддержания и сличения международных и национальных эталонов единиц физических величин, включая стандартные образцы веществ и материалов.
1.2 Настоящее Руководство, в первую очередь, рассматривает выражение неопределенности измерения хорошо определенной физической величины, характеризуемой единственным значением. Если предмет изучения нельзя охарактеризовать единственным значением, а лишь некоторым распределением значений или если он характеризуется зависимостью от одного или более параметров (например, представляет собой временной процесс), то измеряемыми величинами, требуемыми для его описания, являются параметры распределения или зависимости.
1.3 Настоящее Руководство распространяется также на оценивание и выражение неопределенности результатов теоретических расчетов и испытаний, методов измерений, анализа сложных систем. Поскольку в таких приложениях результат оценивания величины и его неопределенность могут быть умозрительными и полностью основанными на гипотетических данных, то термин «результат измерений», используемый в настоящем Руководстве, следует толковать в этом более широком контексте.
1.4 Настоящее Руководство устанавливает общие правила оценивания и выражения неопределенности измерения и не содержит подробных указаний для конкретных измерений. В нем не рассматривается также вопрос, каким образом полученная оценка неопределенности результата конкретного измерения может быть использована в дальнейшем, например, для вывода о сопоставимости данного результата с результатами аналогичных измерений, для установления допусков в технологическом процессе, для заключения о соблюдении или несоблюдении установленных требований безопасности. Подобные вопросы, связанные со специфическими областями измерений или с конкретным использованием количественных оценок неопределенности, могут рассматриваться в других стандартах, основанных на настоящем Руко-
водстве5. Такие стандарты могут представлять собой упрощенные версии настоящего Руководства, но они должны содержать в себе все необходимые сведения, исходя из требуемого уровня точности и сложности измерений, на которые они распространяются.
Примечание — Возможны случаи, когда концепция неопределенности измерения неприменима в полном объеме, например при определении точности метода испытаний (см., например, [5]).
2 Термины и определения
2.1 Общие метрологические термины
Определения ряда общих метрологических терминов по тематике настоящего Руководства, таких как «измеримая величина», «измеряемая величина» и «погрешность измерения», приведены в приложении В. Эти определения взяты из Международного словаря основных и общих терминов в метрологии [6]6. Кроме того, в приложении С приведены определения ряда основных статистических терминов, взятых большей частью из ИСО 3534-1 [7]. Когда один из этих метрологических или статистических терминов (или терминов, близко с ними связанных) встречается в тексте впервые (начиная с раздела 3), он выделяется полужирным шрифтом, а в скобках приводится номер подраздела, в котором дано его определение.
Ввиду особой важности для настоящего Руководства термина «неопределенность измерения» его определение дано как в приложении В, так и в 2.2.3. Определения других наиболее важных для настоящего Руководства терминов даны в 2.3.1 — 2.3.6. В этих подразделах так же, как и в приложениях В и С, выделение в термине слова скобками означает, что данное слово, если только это не приводит к путанице, может быть опущено.
2.2 Термин «неопределенность»
Понятие неопределенности подробно рассматривается в разделе 3 и приложении D.
2.2.1 Слово «неопределенность» означает сомнение, и, таким образом, в широком смысле «неопределенность измерения» означает сомнение в достоверности результата измерения. Специальные термины для величин, характеризующих количественную меру такого сомнения (например, стандартного отклонения), отсутствуют, поэтому слово «неопределенность» используют и в указанном широком смысле, и в смысле некоторой количественной меры.
2.2.2 В настоящем Руководстве слово «неопределенность», используемое без прилагательного, относится как к общему понятию неопределенности, так и к любым количественным мерам неопределенности. Если необходимо уточнить, какая количественная мера имеется в виду, то для этого используется соответствующее прилагательное.
2.2.3 Для применения в настоящем Руководстве и в международном словаре VIM [6] (VIM:1993, словарная статья 3.9) принято следующее формальное определение термина «неопределенность измерения»:
неопределенность (измерения) [uncertainty (of measurement)]: Параметр, относящийся к результату измерения и характеризующий разброс значений, которые могли бы быть обоснованно приписаны измеряемой величине.
Примечание 1 — Параметром может быть, например, стандартное отклонение (или величина, пропорциональная стандартному отклонению) или полуширина интервала, которому соответствует заданный уровень доверия.
Примечание 2 — Неопределенность измерения, как правило, включает в себя много составляющих. Некоторые из них могут быть оценены из статистического распределения результатов ряда измерений и описаны выборочными стандартными отклонениями. Другие составляющие, которые также могут быть описаны стандартными отклонениями, оценивают, исходя из основанных на опыте предположений или иной информации о виде закона распределения.
ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008
Примечание 3 — Предполагается, что результат измерения является лучшей оценкой измеряемой величины, а все составляющие неопределенности, включая обусловленные систематическими эффектами (разного рода поправками, используемым эталоном сравнения), вносят вклад в разброс значений измеряемой величины.
2.2.4 Определение неопределенности измерения, приведенное в 2.2.3, является рабочим, привязанным, в первую очередь, к понятиям результата измерения и оценки его неопределенности. Однако оно не противоречит использованию понятия неопределенности измерений в других смыслах, таких как:
- мера возможной погрешности оценки измеряемой величины, полученной как результат измерения;
- оценка, характеризующая диапазон значений, в пределах которого находится истинное значение измеряемой величины (VIM:1984,3.09).
Хотя оба эти традиционно используемые представления справедливы как идеализация, основной акцент в них сделан на неизвестные величины: «погрешность» результата измерения и «истинное значение» измеряемой величины (в противоположность известной оценке этой величины) соответственно. Тем не менее, независимо от того, какой смысл вкладывают в понятие неопределенности, для оценивания составляющей неопределенности всегда используют одни и те же данные и имеющуюся информацию (см. также раздел Е.5).
2.3 Термины, вводимые Руководством
Как правило, пояснения терминов, вводимых настоящим Руководством, даны при их первом употреблении в тексте. Однако для удобства пользования Руководством определения этих терминов собраны в настоящем подразделе.
Примечание — Более полное рассмотрение вводимых в настоящем подразделе терминов содержится: для термина по 2.3.2 — в 3.3.3 и 4.2; для термина по 2.3.3 — в 3.3.3 и 4.3; для термина по 2.3.4 — в разделе 5 [см. также формулы (10) и (13)]; для термина по 2.3.6 — в разделе 6.
2.3.1 стандартная неопределенность (standard uncertainty): Неопределенность результата измерения, выраженная в виде стандартного отклонения.
2.3.2 оценивание (неопределенности) типа А [Туре A evaluation (of uncertainty)]: Метод оценивания неопределенности путем статистического анализа ряда наблюдений.
2.3.3 оценивание (неопределенности) типа В [Туре В evaluation (of uncertainty)]: Метод оценивания неопределенности, отличный от статистического анализа ряда наблюдений.
2.3.4 суммарная стандартная неопределенность (combined standard uncertainty): Стандартная неопределенность результата измерения, полученного из значений ряда других величин, равная положительному квадратному корню взвешенной суммы дисперсий или ковариаций этих величин, весовые коэффициенты при которых определяются зависимостью изменения результата измерения от изменений этих величин.
2.3.5 расширенная неопределенность (expanded uncertainty): Величина, определяющая интервал вокруг результата измерения, который, как ожидается, содержит в себе большую часть распределения значений, что с достаточным основанием могут быть приписаны измеряемой величине.
Примечание 1 —Долю распределения, охватываемую интервалом, можно рассматривать как вероятность охвата или уровень доверия для данного интервала.
Примечание 2 — Чтобы сопоставить интервалу, рассчитанному через расширенную неопределенность, некоторое значение уровня доверия, необходимо сделать в явном или неявном виде предположение о форме распределения, характеризуемого результатом измерения и его суммарной стандартной неопределенностью. Уровень доверия, поставленный в соответствие этому интервалу, может быть известен только в той мере, в которой оправдано сделанное предположение о форме распределения.
Примечание 3 — В параграфе 5 Рекомендаций INC-1 (1980) расширенная неопределенность названа общей неопределенностью.
2.3.6 коэффициент охвата (coverage factor): Коэффициент, на который умножают суммарную стандартную неопределенность для получения расширенной неопределенности.
Примечание — Коэффициент охвата обычно принимает значения от 2 до 3.
3 Основные понятия
Дополнительное рассмотрение основных понятий можно найти в приложении D, в котором основное внимание уделено вопросам сопоставления (в том числе, графического) «истинного» значения, погрешности и неопределенности, и в приложении Е, где исследуются необходимость разработки и статистическая
3
база Рекомендации INC-1 (1980), на которой основано настоящее Руководство. В приложении J приведен словарь основных математических символов, используемых в настоящем Руководстве.
3.1 Измерение
3.1.1 Целью измерения (В.2.5) является определение значения (В.2.2) измеряемой величины (В.2.9), т.е. значения конкретной величины (В.2.1, примечание 1), которую надо измерить. Поэтому измерению предшествует определение измеряемой величины, метода измерения (В.2.7) и методики измерения (измерительной процедуры) (В.2.8).
Примечание — Термин «истинное значение» (см. приложение D) не используется в настоящем Руководстве по причинам, указанным в D.3.5. Термины «значение измеряемой величины» и «истинное значение измеряемой величины» рассматриваются как эквивалентные.
3.1.2 Обычно результат измерения (В.2.11) является только аппроксимацией или оценкой (С.2.26) значения измеряемой величины и, таким образом, будет полным только в том случае, если он сопровождается указанием неопределенности (В.2.18) этой оценки.
3.1.3 На практике определение (дефиниция) измеряемой величины зависит от требований кточности измерения (В.2.14). Измеряемую величину следует определять с достаточной полнотой (сучетом необходимой точности измерений), чтобы для всех практических целей, связанных с измерением, значение измеряемой величины было единственным. Именно в таком смысле выражение «значение измеряемой величины» используется в настоящем Руководстве.
Пример — Если длину стального стержня номинальной длины 1 м нужно узнать с точностью до микрона, то определение измеряемой величины должно включать температуру и давление, при которых длина стержня должна быть измерена. Таким образом, определение измеряемой величины должно иметь вид, например: длина стержня при температуре 25,00 °С и давлении 101 325 Па (с указанием, возможно, других необходимых параметров, например способа опирания стержня при измерении). Однако если длина стержня должна быть получена с точностью до миллиметра, то определение измеряемой величины не требует указания температуры, давления и иных аналогичных факторов.
Примечание — Недостаточно полное определение измеряемой величины может привести к росту составляющей неопределенности, которая в этом случае должна быть включена в оценку неопределенности результата измерения (см. D.1.1, D.3.4 и D.6.2).
3.1.4 Во многих случаях результат измерения получают на основе ряда наблюдений, выполненных в условиях повторяемости (В.2.15, примечание 1).
3.1.5 Предполагается, что причиной изменчивости результатов повторных наблюдений являются влияющие величины (В.2.10), от которых может зависеть результат измерений и которые невозможно поддерживать в точности постоянными.
3.1.6 Очень важно правильно составить математическую модель, с помощью которой совокупность повторных наблюдений преобразуется в результат измерения, поскольку помимо наблюдений в нее обычно необходимо включать различные влияющие величины, точные значения которых неизвестны. Эта неизвестность вносит вклад в неопределенность результата измерений наряду с изменчивостью результатов повторных наблюдений и с неточностью самой математической модели.
3.1.7 В настоящем Руководстве измеряемая величина рассматривается как скаляр, т.е. ее значение выражается единственным числом. Распространение на случай связанных между собой величин, определяемых одновременно в одном измерении, требует перейти от рассмотрения измеряемой скалярной величины и ее дисперсии (С.2.11, С.2.20, С.3.2) к измеряемой векторной величине и ковариационной матрице (С.3.5). В настоящем Руководстве измерение векторной величины рассматривается только в примерах (см. Н.2, Н.З и Н.4).
3.2 Погрешности, случайные и систематические эффекты, поправки
3.2.1 Погрешность (В.2.19) результата измерения обусловлена несовершенством измерительной процедуры. Традиционно погрешность рассматривают как сумму двух составляющих: случайной (В.2.20) и систематической (В.2.21).
Примечание — Погрешность является идеализированным понятием, поскольку на практике ее точное значение неизвестно.
3.2.2 Предполагается, что случайная погрешность возникает из непредсказуемых временных или пространственных изменений влияющих величин. Следствием таких изменений, называемых далее случайными эффектами, являются изменения измеряемой величины при повторных наблюдениях. Хотя случайную погрешность результата измерения нельзя компенсировать введением поправки, ее можно умень-
4
1
Примечание к изданию 2008 г.: В 2005 г. к указанным семи международным организациям присоединилось Международное сотрудничество по аккредитации лабораторий (ИЛАК).
2
Примечание к изданию 2008 г.: В 1995 г. наименования трех международных организаций были изменены. Теперь эти организации имеют следующие наименования: Международная федерация клинической химии и лабораторной медицины (МФКХ); Международная организация по теоретической и прикладной химии (ИЮПАК); Международная организация по теоретической и прикладной физике (ИЮПАП).
3
Примечание к изданию 2008 г.: В настоящее время ссылка на адреса восьми международных организаций, поддержавших разработку Руководства, приведены на сайте Объединенного комитета по разработке руководств в области метрологии (JCGM) http://www.bipm.org/en/committees/jc/jcgm.
4
В оригинале Рекомендация INC-1 (1980) приведена дважды: на французском языке в А.1 и на английском языке в 0.7. Во избежание дублирования подраздел 0.7 Введения из настоящего стандарта исключен.
Издание официальное
5
Примечание к изданию 2008 г.: Ряд таких документов общего и частного характера уже опубликован. Не претендующий на полноту перечень подобных документов можно найти на сайте http://www.bipm.org/en/committees/ jc/jcgm/wglbibliography.html. Кроме того, перечень действующих документов, ссылающихся на Руководство по выражению неопределенности измерений, можно получить, воспользовавшись полнотекстовым поиском на сайтах http://www.iso.org/ и http://www.iec.ch/.
6
Примечание к изданию 2008 г.: Третье издание словаря опубликовано в 2007 г. как Руководство ИСО/МЭК 99 «Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины» [ISO/IEC Guide 99, International vocabulary of metrology — Basic and general concepts and associated terms (VIM)].