ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
НАЦИОНАЛЬНЫЙ
СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
|
ГОСТ
Р
50779.22-2005
(ИСО
2602:1980)
|
СТАТИСТИЧЕСКИЕ
МЕТОДЫ
СТАТИСТИЧЕСКОЕ
ПРЕДСТАВЛЕНИЕ ДАННЫХ
ТОЧЕЧНАЯ
ОЦЕНКА И ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ СРЕДНЕГО
ISO 2602:1980
Statistical interpretation of test results -
Estimation
of the mean - Confidence interval (MOD)
Москва
Стандартинформ
2005
Предисловие
Задачи,
основные принципы и правила проведения работ по государственной стандартизации
в Российской Федерации установлены ГОСТ Р 1.0-92 «Государственная система
стандартизации Российской Федерации. Основные положения» и ГОСТ Р 1.2-92
«Государственная система стандартизации Российской Федерации. Порядок
разработки государственных стандартов»
Сведения
о стандарте
1 ПОДГОТОВЛЕН Техническим комитетом по
стандартизации ТК 125 «Статистические методы в управлении качеством продукции»
и Научно-исследовательским центром контроля и диагностики технических систем на
основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением технического регулирования и стандартизации
Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом
Федерального агентства по техническому регулированию и метрологии от 31 мая
2005 г. № 112-ст
4 Настоящий стандарт
является модифицированным по отношению к международному стандарту ИСО 2602:1980
«Статистическое представление результатов испытаний. Оценка среднего.
Доверительный интервал» (ISO 2602:1980 «Statistical interpretation of test results - Estimation of the mean - Confidence interval», MOD) путем включения отдельных фраз, которые выделены
в тексте курсивом, с целью гармонизации с национальными стандартами.
Наименование
настоящего стандарта изменено относительно наименования указанного
международного стандарта для приведения в соответствие с ГОСТ
1.5 (подраздел 3.6)
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в
указателе «Национальные стандарты», а текст изменений -
в информационных указателях «Национальные стандарты». В случае пересмотра
или отмены настоящего стандарта соответствующая информация будет опубликована в
информационном указателе «Национальные стандарты»
СОДЕРЖАНИЕ
|
1 Область применения. 2
2 Нормативные ссылки. 2
3 Термины и определения. 2
4 Условия применения методов. 2
5 Точечная оценка среднего. 3
6 Доверительный интервал для среднего. 3
7 Представление результатов. 5
Приложение А Доверительный
интервал для среднего на основе размахов. 6
|
ГОСТ Р 50779.22-2005
(ИСО 2602:1980)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические
методы
СТАТИСТИЧЕСКОЕ
ПРЕДСТАВЛЕНИЕ ДАННЫХ
Точечная
оценка и доверительный интервал для среднего
Statistical interpretation of
test results - Estimation of the mean - Confidence interval
Дата
введения - 2005-07-01
1
Область применения
Настоящий
стандарт устанавливает методы определения по результатам испытаний точечной
оценки и доверительного интервала среднего (далее - среднее) генеральной
совокупности.
2
Нормативные ссылки
В
настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ
Р 50779.10-2000 (ИСО 3534-1-93) Статистические
методы. Вероятность и основы статистики. Термины и определения (ИСО
3534-1:1993, IDТ)
ГОСТ
Р 50779.21-2004 Статистические методы. Правила определения и методы расчета
статистических характеристик по выборочным данным. Часть 1. Нормальное
распределение (ИСО 2854:1976, NEQ)
Примечание
- При пользовании настоящим стандартом целесообразно проверить действие
ссылочных стандартов по указателю «Национальные стандарты», составленному по
состоянию на 1 января текущего года, и по соответствующим информационным
указателям, опубликованным в текущем году. Если ссылочный стандарт заменен
(изменен), то при пользовании настоящим стандартом следует руководствоваться
замененным (измененным) стандартом. Если ссылочный стандарт отменен без замены,
то положение, в котором дана ссылка на него, применяют в части, не затрагивающей
эту ссылку.
3
Термины и определения
В
настоящем стандарте применены термины по ГОСТ
Р 50779.10.
4
Условия применения методов
Результаты
испытаний представлены результатами измерений непрерывной величины. Настоящий
стандарт не охватывает обработку результатов испытаний, когда исследуемая
величина является дискретной (например, наличие или отсутствие свойства,
количество дефектов).
Распределение
вероятностей, взятое как математическая модель для генеральной совокупности, -
нормальное распределение, для которого параметры (среднее т и
стандартное отклонение s) неизвестны.
Предположение
о нормальности очень широко используют: распределение результатов, полученных в
условиях испытаний, обычно нормальное или почти нормальное распределение.
Может
быть, однако, полезным проверить предположение о нормальности распределения с
помощью соответствующих методов. Вычисления могут быть упрощены изменением начала
координат или единицы измерения результатов испытаний, но округлять эти
результаты не рекомендуется. Недопустимо отбрасывать любые результаты
наблюдений или применять любые корректировки к очевидно неопределенным
наблюдениям, не подкрепленные доказательствами на экспериментальной,
технической или какой-либо другой основе, которая должна быть четко
установлена.
Метод
испытаний может быть источником систематических ошибок, которые в настоящем
стандарте не определены. Однако существование таких ошибок может сделать
неприменимыми методы, изложенные далее.
В
частности, если имеет место несистематическое смещение, увеличение выборки
размера п не повлияет на смещение.
Методы,
представленные в ГОСТ
Р 50779.21, могут быть использованы в определенных случаях для
идентификации систематических ошибок.
5
Точечная оценка среднего
5.1 Случай несгруппированных
результатов
После
отбрасывания сомнительных результатов серии включают в себя результаты п
измерений хi (где i = 1, 2, 3, ... n), некоторые из которых могут быть
одинаковыми.
Среднее
т основного нормального распределения оценивают как среднее
арифметическое п результатов:
(1)
5.2 Случай
сгруппированных в классы результатов
Когда
число результатов достаточно велико (например, более 50), может быть выгодно
сгруппировать их в классы одинаковой ширины. В определенных случаях результаты
могут быть получены уже сгруппированными в классы.
Частоту
в каждом классе, то есть число результатов в классе, обозначают ni.
Обозначая
число классов к, имеют
(2)
Среднюю
точку класса обозначают yi.
Тогда среднее т оценивают как взвешенное среднее всех средних точек
классов
(3)
6
Доверительный интервал для среднего
Доверительный
интервал для среднего совокупности вычисляют на основе оценок среднего и
стандартного отклонения.
Альтернативный
метод вычисления доверительного интервала с использованием размахов дан в
приложении А.
6.1 Оценка стандартного отклонения
6.1.1 Случай несгруппированных результатов
Оценку
s
стандартного отклонения s, вычисляемую на основе квадратов отклонений от
среднего арифметического, задают формулой
(4)
где xi - значение i-го измерения (i = 1, 2, 3,... n);
п
- общее число измерений;
-
среднее арифметическое п измерений, вычисленное по формуле (1).
Для
упрощения вычислений рекомендуется использовать формулу
(5)
6.1.2 Случай сгруппированных результатов
В
случае группирования в классы формула для оценки стандартного отклонения имеет
вид
(6)
где уi - средняя точка в i-м классе (i = 1, 2, 3, ... к);
к
- число классов;
п
- общее число измерений;
-
взвешенное среднее всех средних точек классов, вычисленное по формуле (3).
Для
простоты вычислений рекомендуется использовать формулу
(7)
В
случае сгруппированных данных вычисленное значение s может
быть скорректировано (поправка Шеппарда). Поскольку эта поправка при правильно
выбранной ширине класса невелика, ее вводят не всегда.
6.2 Доверительный интервал для среднего
Доверительный
интервал определяется тем, какая выбрана доверительная вероятность 1 - a
(0,95 или 0,99), и тем, какой будет построен интервал (односторонний или
двусторонний).
6.2.1 Двусторонний
доверительный интервал
Двусторонний
доверительный интервал для среднего т совокупности определяют по
следующим формулам:
а)
для доверительной вероятности 0,95:
(8)
б)
для доверительной вероятности 0,99:
(9)
6.2.2 Односторонний
доверительный интервал
Односторонний
доверительный интервал для среднего т совокупности определяют по одной
из следующих формул:
а)
для доверительной вероятности 0,95:
(10)
или
(11)
б)
для доверительной вероятности 0,99:
(12)
или
(13)
При
этом х, если необходимо, может быть заменен на в случае
сгруппированных в классы результатов.
Здесь
t0,975,
t0,995,
t0,95,
t0,99
- квантили распределения Стьюдента с n
= п + 1 степенями свободы.
Их
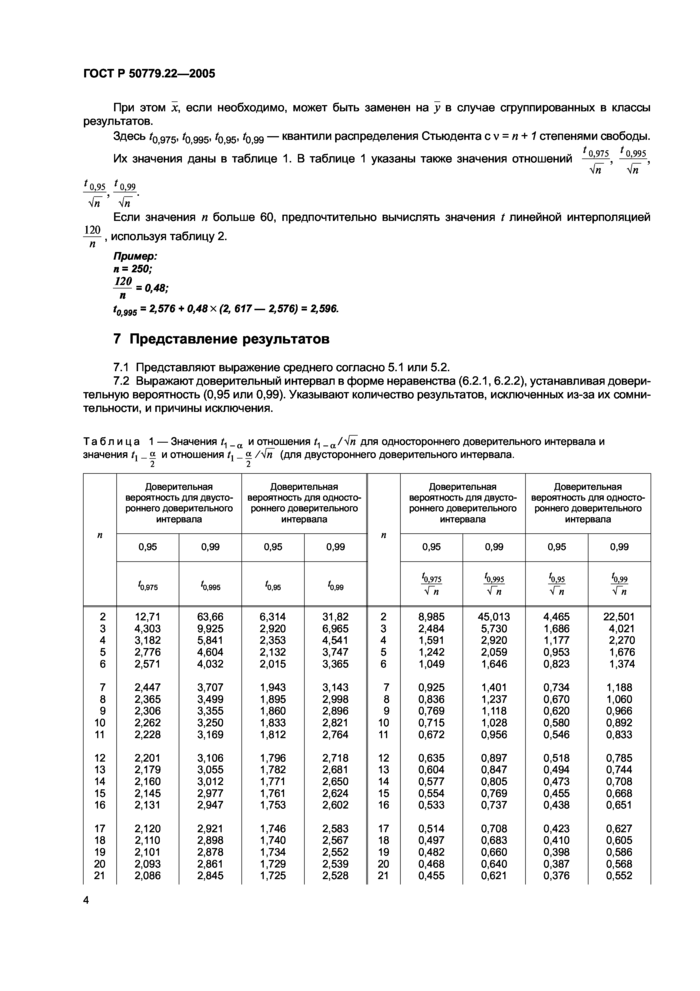
значения даны в таблице 1. В таблице 1 указаны также значения
отношений , , , .
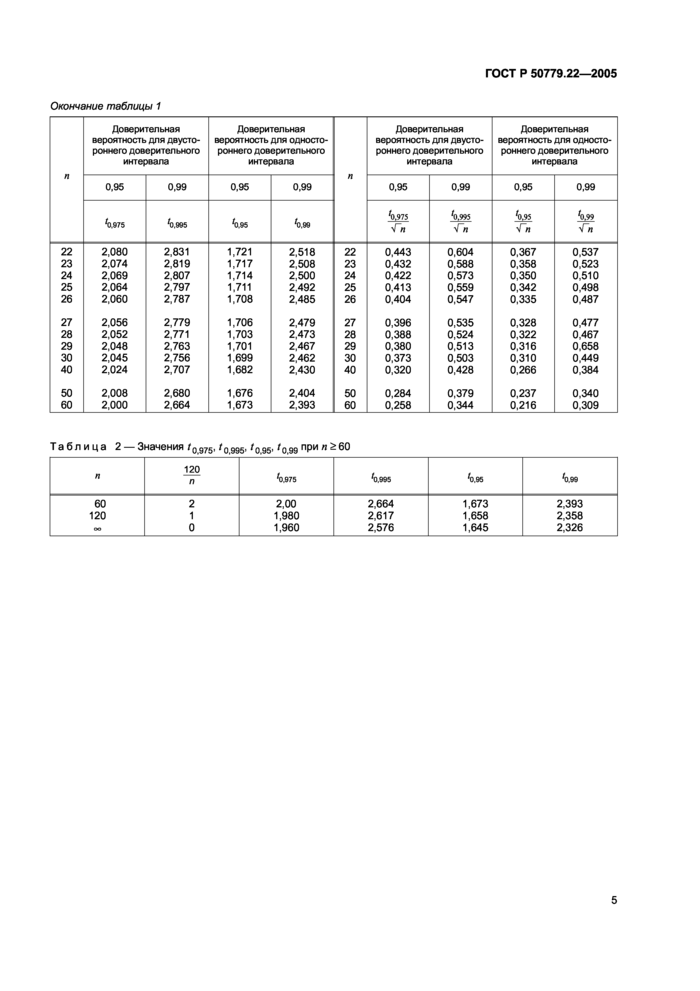
Если
значения п больше 60, предпочтительно вычислять значения t линейной интерполяцией , используя таблицу 2.
Пример:
п
= 250;
t0,995 = 2,576 + 0,48 ´ (2,617 - 2,576) = 2,596.
7
Представление результатов
7.1 Представляют выражение среднего согласно 5.1 или 5.2.
7.2 Выражают доверительный интервал в форме
неравенства (6.2.1,
6.2.2),
устанавливая доверительную вероятность (0,95 или 0,99). Указывают количество
результатов, исключенных из-за их сомнительности, и причины исключения.
Таблица
1 - Значения t1-a и отношения t1-a/ для одностороннего доверительного интервала и значения и отношения / (для двустороннего доверительного интервала.
|
п
|
Доверительная вероятность для
двустороннего доверительного интервала
|
Доверительная вероятность для
одностороннего доверительного интервала
|
n
|
Доверительная вероятность для двустороннего
доверительного интервала
|
Доверительная вероятность для
одностороннего доверительного интервала
|
|
0,95
|
0,99
|
0,95
|
0,99
|
0,95
|
0,99
|
0,95
|
0,99
|
|
t0,975
|
t0,995
|
t0,95
|
t0,99
|
t0,975
|
t0,995
|
t0,95
|
t0,99
|
|
2
|
12,71
|
63,66
|
6,314
|
31,82
|
2
|
8,985
|
45,013
|
4,465
|
22,501
|
|
3
|
4,303
|
9,925
|
2,920
|
6,965
|
3
|
2,484
|
5,730
|
1,686
|
4,021
|
|
4
|
3,182
|
5,841
|
2,353
|
4,541
|
4
|
1,591
|
2,920
|
1,177
|
2,270
|
|
5
|
2,776
|
4,604
|
2,132
|
3,747
|
5
|
1,242
|
2,059
|
0,953
|
1,676
|
|
6
|
2,571
|
4,032
|
2,015
|
3,365
|
6
|
1,049
|
1,646
|
0,823
|
1,374
|
|
7
|
2,447
|
3,707
|
1,943
|
3,143
|
7
|
0,925
|
1,401
|
0,734
|
1,188
|
|
8
|
2,365
|
3,499
|
1,895
|
2,998
|
8
|
0,836
|
1,237
|
0,670
|
1,060
|
|
9
|
2,306
|
3,355
|
1,860
|
2,896
|
9
|
0,769
|
1,118
|
0,620
|
0,966
|
|
10
|
2,262
|
3,250
|
1,833
|
2,821
|
10
|
0,715
|
1,028
|
0,580
|
0,892
|
|
11
|
2,228
|
3,169
|
1,812
|
2,764
|
11
|
0,672
|
0,956
|
0,546
|
0,833
|
|
12
|
2,201
|
3,106
|
1,796
|
2,718
|
12
|
0,635
|
0,897
|
0,518
|
0,785
|
|
13
|
2,179
|
3,055
|
1,782
|
2,681
|
13
|
0,604
|
0,847
|
0,494
|
0,744
|
|
14
|
2,160
|
3,012
|
1,771
|
2,650
|
14
|
0,577
|
0,805
|
0,473
|
0,708
|
|
15
|
2,145
|
2,977
|
1,761
|
2,624
|
15
|
0,554
|
0,769
|
0,455
|
0,668
|
|
16
|
2,131
|
2,947
|
1,753
|
2,602
|
16
|
0,533
|
0,737
|
0,438
|
0,651
|
|
17
|
2,120
|
2,921
|
1,746
|
2,583
|
17
|
0,514
|
0,708
|
0,423
|
0,627
|
|
18
|
2,110
|
2,898
|
1,740
|
2,567
|
18
|
0,497
|
0,683
|
0,410
|
0,605
|
|
19
|
2,101
|
2,878
|
1,734
|
2,552
|
19
|
0,482
|
0,660
|
0,398
|
0,586
|
|
20
|
2,093
|
2,861
|
1,729
|
2,539
|
20
|
0,468
|
0,640
|
0,387
|
0,568
|
|
21
|
2,086
|
2,845
|
1,725
|
2,528
|
21
|
0,455
|
0,621
|
0,376
|
0,552
|
|
22
|
2,080
|
2,831
|
1,721
|
2,518
|
22
|
0,443
|
0,604
|
0,367
|
0,537
|
|
23
|
2,074
|
2,819
|
1,717
|
2,508
|
23
|
0,432
|
0,588
|
0,358
|
0,523
|
|
24
|
2,069
|
2,807
|
1,714
|
2,500
|
24
|
0,422
|
0,573
|
0,350
|
0,510
|
|
25
|
2,064
|
2,797
|
1,711
|
2,492
|
25
|
0,413
|
0,559
|
0,342
|
0,498
|
|
26
|
2,060
|
2,787
|
1,708
|
2,485
|
26
|
0,404
|
0,547
|
0,335
|
0,487
|
|
27
|
2,056
|
2,779
|
1,706
|
2,479
|
27
|
0,396
|
0,535
|
0,328
|
0,477
|
|
28
|
2,052
|
2,771
|
1,703
|
2,473
|
28
|
0,388
|
0,524
|
0,322
|
0,467
|
|
29
|
2,048
|
2,763
|
1,701
|
2,467
|
29
|
0,380
|
0,513
|
0,316
|
0,658
|
|
30
|
2,045
|
2,756
|
1,699
|
2,462
|
30
|
0,373
|
0,503
|
0,310
|
0,449
|
|
40
|
2,024
|
2,707
|
1,682
|
2,430
|
40
|
0,320
|
0,428
|
0,266
|
0,384
|
|
50
|
2,008
|
2,680
|
1,676
|
2,404
|
50
|
0,284
|
0,379
|
0,237
|
0,340
|
|
60
|
2,000
|
2,664
|
1,673
|
2,393
|
60
|
0,258
|
0,344
|
0,216
|
0,309
|
Таблица 2 - Значения t0,975,
t0,995,
t0,95,
t0,99
при п ³ 60
|
п
|
|
t0,975
|
t0,995
|
t0,95
|
t0,99
|
|
60
|
2
|
2,00
|
2,664
|
1,673
|
2,393
|
|
120
|
1
|
1,980
|
2,617
|
1,658
|
2,358
|
|
¥
|
0
|
1,960
|
2,576
|
1,645
|
2,326
|
Приложение А
(справочное)
Доверительный интервал для среднего на основе
размахов
А.1
Условия применения метода
Если
результаты ранжированы в соответствии с их значениями так, что х1
< х2 < ... < хn, то
W = xn
- x1 (A.1)
является
размахом выборки. Доверительный интервал для среднего совокупности может быть
определен на основе размаха выборки, когда количество измерений мало, например
12 или менее. Практическое удобство вычисления состоит в его быстроте, а
недостаток - в том, что вычисление на основе размахов приводит к более широкому
доверительному интервалу.
А.2
Двусторонний доверительный интервал
Двусторонний
доверительный интервал для среднего т совокупности определяют по
следующим формулам:
а)
при доверительной вероятности 1 - a = 0,95:
(А.2)
б)
при доверительной вероятности 1 - a = 0,99:
(А.3)
Значения
коэффициентов q0,75,
q0,995,
q0,95,
q0,99
даны в таблице А.1.
А.3
Односторонний доверительный интервал
Односторонний
доверительный интервал для среднего т совокупности определяют по одной
из следующих формул:
а)
при доверительной вероятности 1 - a = 0,95:
(А.4)
б)
при доверительной 1 - a = 0,99:
(А.5)
Значения
коэффициентов q1-a
(q0,95,
q0,99)
даны в таблице А.1.
Таблица А.1 - Значения q1-a
для одностороннего доверительного интервала и значения для двустороннего
доверительного интервала
|
п
|
Доверительная вероятность для
двустороннего доверительного интервала
|
Доверительная вероятность для
одностороннего доверительного интервала
|
|
0,95
|
0,99
|
0,95
|
0,99
|
|
q0,975
|
q0,995
|
q0,95
|
q0,99
|
|
2
|
6,353
|
31,828
|
3,157
|
15,910
|
|
3
|
1,304
|
3,008
|
0,885
|
2,111
|
|
4
|
0,717
|
1,316
|
0,529
|
1,023
|
|
5
|
0,507
|
0,843
|
0,388
|
0,685
|
|
6
|
0,399
|
0,628
|
0,312
|
0,523
|
|
7
|
0,333
|
0,507
|
0,263
|
0,429
|
|
8
|
0,288
|
0,429
|
0,230
|
0,366
|
|
9
|
0,255
|
0,374
|
0,205
|
0,322
|
|
10
|
0,230
|
0,333
|
0,186
|
0,288
|
|
11
|
0,210
|
0,302
|
0,170
|
0,262
|
|
12
|
0,194
|
0,277
|
0,158
|
0,241
|
Ключевые
слова: статистические методы, результаты испытаний, оценка
среднего, доверительный интервал, стандартное отклонение, выборка