ГОСТ Р ИСО 5725-2-2002
Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
Распространяется на методы измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающие в качестве результата измерений единственное значение. При этом единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
Переиздание. Март 2009 г.
Оглавление
Предисловие к государственным стандартам Российской Федерации ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002 под общим заголовком «Точность (правильность и прецизионность)
Предисловие к международному стандарту ИСО 5725
Введение к международному стандарту ИСО 5725
1 Область применения
2 Нормативные ссылки
3 Определения
4 Исходная модель и оцениваемые показатели
5 Требования к эксперименту по оценке прецизионности
5.1 Программа эксперимента
5.2 Привлечение лабораторий
5.3 Подготовка материалов
6 Персонал, привлекаемый к участию в эксперименте по оценке прецизионности
6.1 Совет экспертов
6.2 Статистические функции
6.3 Исполнительные функции
6.4 Инспекторы
6.5 Операторы
7 Статистический анализ данных эксперимента по оценке прецизионности
7.1 Предварительные соображения
7.2 Представление результатов и используемые обозначения
7.3 Анализ данных на совместимость и наличие выбросов
7.4 Расчет общего среднего значения и дисперсий
7.5 Установление функциональной зависимости между значениями прецизионности и средним значением m для уровня
7.6 Статистический анализ как поэтапная процедура
7.7 Доклад совету экспертов и принимаемые им решения
8 Статистические таблицы
Приложение А Условные обозначения и сокращения, используемые в ГОСТ Р ИСО 5725
Приложение В Примеры статистического анализа экспериментов по оценке прецизионности
В.1 Пример 1. Определение содержания серы в угле (несколько уровней без недостающих данных и без выбросов)
В.2 Пример 2. Точка размягчения смолы (несколько уровней с недостающими данными)
В.3 Пример 3. Термометрическое титрование креозотового масла (несколько уровней с выбросами)
Приложение С Библиография
50 страниц
| Дата введения | 01.11.2002 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Строительство
- Раздел Экология
Организации:
| 23.04.2002 | Утвержден | Госстандарт России | 161-ст |
|---|---|---|---|
| Разработан | ВНИИстандарт Госстандарта России | ||
| Разработан | ВНИИМС (ВНПО Агропромснаб ) | ||
| Разработан | ВНИИКИ | ||
| Издан | ИПК Издательство стандартов | 2002 г. | |
| Издан | Стандартинформ | 2009 г. |
Accuracy (trueness and precision) of measurement methods and results. Part 2. Basic method for determination of repeability and reproducibility of a standard measurement method
РМГ 29-99Государственная система обеспечения единства измерений. Метрология. Основные термины и определения. Заменен на РМГ 29-2013.ГОСТ Р ИСО/МЭК 17025-2000Общие требования к компетентности испытательных и калибровочных лабораторий. Заменен на ГОСТ Р ИСО/МЭК 17025-2006.- ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
- ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
- ГОСТ Р ИСО 5725-4-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений
- ГОСТ Р ИСО 5725-5-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
- ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике
ГОСТ Р 8.563-96Государственная система обеспечения единства измерений. Методики выполнения измерений. Заменен на ГОСТ Р 8.563-2009.- ГОСТ Р ИСО/МЭК 17025-2006 Общие требования к компетентности испытательных и калибровочных лабораторий
- Показать все
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16
стр. 17

стр. 18

стр. 19

стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26
стр. 27

стр. 28

стр. 29
стр. 30
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОЧНОСТЬ
(ПРАВИЛЬНОСТЬ
И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ
И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Часть 2
Основной метод определения
повторяемости и воспроизводимости стандартного
метода измерений
|
Москва Стандартинформ 2009 |
Предисловие
1 Разработан Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологической службы» Госстандарта России (ВНИИМС), Всероссийским научно-исследовательским институтом стандартизации (ВНИИСтандарт), Всероссийским научно-исследовательским институтом классификации, терминологии и информации по стандартизации и качеству (ВНИИКИ) Госстандарта России
ВНЕСЕН Управлением метрологии и Научно-техническим управлением Госстандарта России
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 23 апреля 2002 г. № 161-ст
3 Настоящий стандарт представляет собой полный аутентичный текст международного стандарта ИСО 5725-1:1994 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений»
4 ВВЕДЕН ВПЕРВЫЕ
5 ПЕРЕИЗДАНИЕ. Март 2009 г.
СОДЕРЖАНИЕ
|
Предисловие к государственным стандартам Российской Федерации ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002 под общим заголовком «точность (правильность и прецизионность) методов и результатов измерений». 2 Предисловие к международному стандарту исо 5725. 5 Введение к международному стандарту исо 5725. 6 1 Область применения. 7 2 Нормативные ссылки. 8 3 Определения. 8 4 Исходная модель и оцениваемые показатели. 8 5 Требования к эксперименту по оценке прецизионности. 9 5.1 Программа эксперимента. 9 5.2. Привлечение лабораторий. 10 5.3 Подготовка материалов. 11 6 Персонал, привлекаемый к участию в эксперименте по оценке прецизионности. 12 6.1 Совет экспертов. 12 6.2 Статистические функции. 12 6.3 Исполнительные функции. 13 6.4 Инспекторы.. 13 6.5 Операторы.. 14 7 Статистический анализ данных эксперимента по оценке прецизионности. 14 7.1 Предварительные соображения. 14 7.2 Представление результатов и используемые обозначения. 15 7.3 Анализ данных на совместимость и наличие выбросов. 17 7.4 Расчет общего среднего значения и дисперсий. 23 7.5 Установление функциональной зависимости между значениями прецизионности и средним значением т для уровня. 24 7.6 Статистический анализ как поэтапная процедура. 28 7.7 Доклад совету экспертов и принимаемые им решения. 31 8 Статистические таблицы.. 32 Приложение а. Условные обозначения и сокращения, используемые в ГОСТ Р ИСО 5725. 35 Приложение в. Примеры статистического анализа экспериментов по оценке прецизионности. 37 В.1 Пример 1. Определение содержания серы в угле (несколько уровней без недостающих данных и без выбросов) 37 В.2 Пример 2. Точка размягчения смолы (несколько уровней с недостающими данными) 41 В.3 Пример 3 - Термометрическое титрование креозотового масла (несколько уровней с выбросами) 46 Приложение С. Библиография. 51 |
ПРЕДИСЛОВИЕ К ГОСУДАРСТВЕННЫМ СТАНДАРТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002 ПОД ОБЩИМ ЗАГОЛОВКОМ «ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ»
Целью разработки Государственных стандартов Российской Федерации ГОСТ Р ИСО 5725-1-2002, ГОСТ Р ИСО 5725-2-2002, ГОСТ Р ИСО 5725-3-2002, ГОСТ Р ИСО 5725-4-2002, ГОСТ Р ИСО 5725-5-2002, ГОСТ Р ИСО 5725-6-2002, далее - ГОСТ Р ИСО 5725, является прямое применение в Российской Федерации шести частей основополагающего Международного стандарта ИСО 5725 под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений» в практической деятельности по метрологии (разработке, аттестации и применению методик выполнения измерений), стандартизации методов контроля (испытаний, измерений, анализа), испытаниям продукции, в том числе для целей подтверждения соответствия, оценке компетентности испытательных лабораторий согласно требованиям ГОСТ Р ИСО/МЭК 17025-2000*.
_____________
* С 1 июля 2007 г. введен в действие ГОСТ Р ИСО/МЭК 17025-2006.
ГОСТ Р ИСО 5725 представляет собой полный аутентичный текст шести частей международного стандарта ИСО 5725, в том числе:
ГОСТ Р ИСО 5725-1-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения»;
ГОСТ Р ИСО 5725-2-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений»;
ГОСТ Р ИСО 5725-3-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-4-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений»;
ГОСТ Р ИСО 5725-5-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике».
Каждая часть содержит аутентичный перевод предисловия и введения к международному стандарту ИСО 5725, а также предисловие к государственным стандартам Российской Федерации (ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002) и издается самостоятельно.
Пользование частями 2 - 6 ГОСТ Р ИСО 5725 в отдельности возможно только совместно с частью 1 (ГОСТ Р ИСО 5725-1), в которой установлены основные положения и определения, касающиеся всех частей ГОСТ Р ИСО 5725.
В соответствии с основными положениями ИСО 5725-1 (пункт 1.2) настоящий стандарт распространяется на методы измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающие в качестве результата измерений единственное значение. При этом это единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
Стандарты ИСО 5725 могут применяться для оценки точности выполнения измерений различных физических величин, характеризующих измеряемые свойства того или иного объекта, в соответствии со стандартизованной процедурой. При этом в пункте 1.2 ИСО 5725-1 особо отмечено, что стандарт может применяться для оценки точности выполнения измерений состава и свойств очень широкой номенклатуры материалов, включая жидкости, порошкообразные и твердые материалы - продукты материального производства или существующие в природе, при условии, что учитывают любую неоднородность материала.
Применяемый в международных стандартах термин «стандартный метод измерений» адекватен отечественному термину «стандартизованный метод измерений».
В ИСО 5725:1994 - 1998 и ИСО/МЭК 17025-99 понятие «метод измерений» («measurement method») включает совокупность операций и правил, выполнение которых обеспечивает получение результатов с известной точностью. Таким образом, понятие «метод измерений» по ИСО 5725 и ИСО/МЭК 17025 адекватно понятию «методика выполнения измерений (МВИ)» по ГОСТ Р 8.563-96 «Государственная система обеспечения единства измерений. Методики выполнения измерений» (пункт 3.1) и соответственно значительно шире по смыслу, чем определение термина «метод измерений» в Рекомендации по межгосударственной стандартизации РМГ 29-99 «Государственная система обеспечения единства измерений. Метрология. Основные термины и определения» (пункт 7.2).
Более того, в оригинале ИСО 5725 очень часто употребляется в качестве понятия «метод измерений» и английский термин «test method», перевод которого на русский язык - «метод испытаний» (см. в оригинале примечание 1 к пункту 3.2 ИСО 5725-1) и который по смыслу совпадает с термином 6.2 ИСО 5725-1 «standard measurement method» (стандартизованный метод измерений). Соответственно в качестве термина «результат измерений» в оригинале стандарта чаще используется английский термин «test result» (см. пункт 3.2 ИСО 5725-1), причем в контексте как с термином «test method» (см. пункт 3.2), так и с термином «measurement method» (см. в оригинале, например, пункты 1.2 или 7.2.1 ИСО 5725-1).
При этом следует иметь в виду, что область применения ИСО 5725 - точность стандартизованных методов измерений, в том числе предназначенных для целей испытаний продукции, позволяющих количественно оценить характеристики свойств (показателей качества и безопасности) объекта испытаний (продукции). Именно поэтому во всех частях стандарта результаты измерений характеристик образцов, взятых в качестве выборки из партии изделий (или проб, отобранных из партии материала), являются основой для получения результатов испытаний всей партии (объекта испытаний). Когда объектом испытаний является конкретный образец (test speciment, sample), результаты измерений и испытаний могут совпадать. Такой подход имеет место в примерах по определению показателей точности стандартного (стандартизованного) метода измерений, содержащихся в ИСО 5725.
Следует отметить, что в отечественной метрологии точность (accuracy) и погрешность (error) результатов измерений, как правило, определяются сравнением результата измерений с истинным или действительным (условно истинным) значением измеряемой физической величины (являющимися фактически эталонными значениями измеряемых величин, выраженными в узаконенных единицах).
В условиях отсутствия необходимых эталонов, обеспечивающих воспроизведение, хранение и передачу соответствующих значений единиц величин, необходимых для оценки погрешности (точности) результатов измерений, и в отечественной, и в международной практике за действительное значение зачастую принимают общее среднее значение (математическое ожидание) установленной (заданной) совокупности результатов измерений. В ИСО 5725 эта ситуация отражена в термине «принятое опорное значение» (см. пункты 3.5 и 3.6 ГОСТ Р ИСО 5725-1) и рекомендуется ГОСТ Р ИСО 5725-1 для использования в этих случаях и в отечественной практике.
Термины «правильность» (trueness) и «прецизионность» (precision) в отечественных нормативных документах по метрологии до настоящего времени не использовались. При этом «правильность» - степень близости результата измерений к истинному или условно истинному (действительному) значению измеряемой величины или в случае отсутствия эталона измеряемой величины - степень близости среднего значения, полученного на основании большой серии результатов измерений (или результатов испытаний) к принятому опорному значению. Показателем правильности обычно является значение систематической погрешности (см. пункт 3.7 ГОСТ Р ИСО 5725-1).
В свою очередь «прецизионность» - степень близости друг к другу независимых результатов измерений, полученных в конкретных установленных условиях. Эта характеристика зависит только от случайных факторов и не связана с истинным или условно истинным значением измеряемой величины (см. пункт 3.12 ГОСТ Р ИСО 5725-1). Мера прецизионности обычно вычисляется как стандартное (среднеквадратическое) отклонение результатов измерений, выполненных в определенных условиях. Количественные значения мер прецизионности существенно зависят от заданных условий. Экстремальные показатели прецизионности - повторяемость, сходимость (repeatability) и воспроизводимость (reproducibility) регламентируют и в отечественных нормативных документах, в том числе в большинстве государственных стандартов на методы контроля (испытаний, измерений, анализа) (см. пункты 3.12 - 3.20 ГОСТ Р ИСО 5725-1).
В соответствии с ИСО 5725 цель государственных стандартов ГОСТ Р ИСО 5725 состоит в том, чтобы:
а) изложить основные положения, которые следует иметь в виду при оценке точности (правильности и прецизионности) методов и результатов измерений при их применении, а также при планировании экспериментов по оценке различных показателей точности (ГОСТ Р ИСО 5725-1);
б) регламентировать основной способ экспериментальной оценки повторяемости (сходимости) и воспроизводимости методов и результатов измерений (ГОСТ Р ИСО 5725-2);
в) регламентировать процедуру получения промежуточных показателей прецизионности методов и результатов измерений, изложив условия их применения и методы оценки (ГОСТ Р ИСО 5725-3);
г) регламентировать основные способы определения правильности методов и результатов измерений (ГОСТ Р ИСО 5725-4);
д) регламентировать для применения в определенных обстоятельствах несколько альтернатив основным способам (ГОСТ Р ИСО 5725-2 и ГОСТ Р ИСО 5725-4) определения прецизионности и правильности методов и результатов измерений, приведенных в ГОСТ Р ИСО 5725-5;
е) изложить некоторые практические применения показателей правильности и прецизионности (ГОСТ Р ИСО 5725-6).
Представленные в виде таблицы рекомендации по применению основных положений ГОСТ Р ИСО 5725 в деятельности по метрологии, стандартизации, испытаниям, оценке компетентности испытательных лабораторий со ссылками на нормы государственных стандартов Российской Федерации, содержащих требования к выполнению соответствующих работ, приведены в приложении к предисловию в ГОСТ Р ИСО 5725-1.
Алгоритм проведения экспериментов по оценке повторяемости, воспроизводимости, промежуточных показателей прецизионности, показателей правильности (характеристик систематической погрешности) методов и результатов измерений рекомендуется внедрять через программы экспериментальных метрологических исследований показателей точности (характеристик погрешности) результатов измерений, выполняемых по разрабатываемой МВИ, и (или) через программы контроля показателей точности применяемых МВИ.
Использование приведенных в приложениях А к каждому стандарту условных обозначений в качестве обязательных рекомендуется только для тех показателей точности, которые до настоящего времени в отечественной метрологической практике не использовались (например, для показателей по пунктам 3.9 - 3.12 ГОСТ Р ИСО 5725-1). Для остальных показателей и критериев используемые в ГОСТ Р ИСО 5725 условные обозначения, как правило, могут применяться наряду с условными обозначениями этих показателей и критериев, принятых в действующих отечественных документах (например, предел повторяемости (сходимости) с условным обозначением r по пункту 3.16 ГОСТ Р ИСО 5725-1 наряду с условным обозначением d, принятым для этого показателя в ряде рекомендаций по метрологии, а также в государственных стандартах на методы испытаний продукции).
ПРЕДИСЛОВИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
Международная организация по стандартизации (ИСО) является Всемирной федерацией национальных организаций по стандартизации (комитетов - членов ИСО). Разработка международных стандартов обычно осуществляется техническими комитетами ИСО. Каждый член ИСО, заинтересованный в деятельности соответствующего технического комитета, имеет право быть представленным в этом комитете. Правительственные и неправительственные международные организации, сотрудничающие с ИСО, также принимают участие в этой работе. ИСО тесно сотрудничает с Международной электротехнической комиссией (МЭК) по всем вопросам стандартизации в области электротехники.
Проекты международных стандартов, принятые техническими комитетами, направляются техническим комитетам - членам ИСО на голосование перед их утверждением Советом ИСО в качестве международных стандартов. Стандарты утверждаются в качестве международных в соответствии с установленными в ИСО требованиями: в случае их одобрения по меньшей мере 75 % комитетов - членов ИСО, принимавших участие в голосовании.
Международный стандарт ИСО 5725-2 был подготовлен Техническим комитетом ИСО/ТК 69 «Применение статистических методов», Подкомитетом ПК 6 «Методы и результаты измерений».
ИСО 5725 состоит из следующих частей под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений»:
Часть 1. Основные положения и определения
Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
Часть 4. Основные методы определения правильности стандартного метода измерений
Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
Часть 6. Использование значений точности на практике
ИСО 5725 (части 1 - 6) в совокупности аннулирует и заменяет ИСО 5725:1986, область распространения которого была расширена включением правильности (в дополнение к прецизионности) и условий промежуточной прецизионности (в дополнение к условиям повторяемости и воспроизводимости).
Приложение А является обязательным для настоящей части ИСО 5725. Приложения В и С - справочные.
ВВЕДЕНИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
0.1 В ИСО 5725 для описания точности метода измерений используются два термина: «правильность» и «прецизионность». Термин «правильность» характеризует степень близости среднего арифметического значения большого числа результатов измерений к истинному или принятому опорному значению, термин «прецизионность» - степень близости результатов измерений друг к другу.
0.2 Общие соображения об этих понятиях представлены в ИСО 5725-1 и поэтому здесь не повторяются. Эта часть ИСО 5725 должна применяться в сочетании с ИСО 5725-1, поскольку в ней даны определения и общие положения.
0.3 Настоящая часть ИСО 5725 касается исключительно оценок, выполняемых с помощью стандартных отклонений повторяемости и воспроизводимости. Несмотря на то, что для оценки прецизионности при определенных обстоятельствах применяют эксперименты и других типов (например, эксперимент с разделенными уровнями), их не рассматривают в настоящей части ИСО 5725, так как они скорее являются предметом ИСО 5725-5. В настоящей части ИСО 5725-2 также не представлены какие-либо другие показатели прецизионности, являющиеся промежуточными между двумя главными показателями: стандартными отклонениями повторяемости и воспроизводимости; промежуточные показатели описаны в ИСО 5725-3.
0.4 При определенных условиях данные, полученные из эксперимента, выполняемого с целью оценки прецизионности, используют также для оценки правильности. Оценку правильности не рассматривают в настоящей части ИСО 5725-2; все аспекты оценки правильности являются предметом ИСО 5725-4.
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ)
МЕТОДОВ
И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Часть 2
Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
Accuracy (trueness and
precision) of measurement methods and results. Part 2.
Basic method for the determination of repeatability and reproducibility of a
standard measurement method.
Дата введения 2002-11-01
1 Область применения
1.1 Настоящий стандарт:
- описывает общие принципы планирования совместных межлабораторных экспериментов, предназначенных для количественной оценки прецизионности методов измерений;
- детально описывает основной алгоритм количественной оценки прецизионности методов измерений в повседневной практике;
- является руководством для персонала, имеющего отношение к планированию эксперимента, осуществлению и анализу результатов измерений по оценке прецизионности.
Примечание 1 - Модификации данного основного метода, предусмотренные для конкретных целей, представлены в других частях ГОСТ Р ИСО 5725.
В приложении В приведены практические примеры экспериментальной оценки прецизионности методов измерений.
1.2 Настоящий стандарт распространяется на методы измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающие в качестве результата измерений единственное значение. При этом единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
1.3 Предполагают, что при планировании и осуществлении эксперимента по оценке прецизионности соблюдены все принципы, установленные ГОСТ Р ИСО 5725-1. Основной метод предусматривает получение и использование одного и того же количества результатов измерений в каждой лаборатории при анализе проб (образцов), соответствующих одним и тем же уровням измеряемой характеристики (испытуемого параметра); т.е. имеется в виду сбалансированный эксперимент с однородными уровнями. Основной метод применяют к процедурам, которые были стандартизованы и регулярно используются во многих лабораториях.
Примечание 2 - Приводятся рабочие примеры для демонстрации сбалансированных однородных серий результатов измерений, даже несмотря на то, что в одном примере было обработано разное количество параллельных определений из расчета на базовый элемент (несбалансированность), а в другом некоторые данные были упущены. Это имеет место в случае, если эксперимент, запланированный как сбалансированный, может оказаться на самом деле несбалансированным, в частности, поскольку при анализе данных выявляются также квазивыбросы и выбросы.
1.4 В качестве подходящего основания для интерпретации и анализа результатов измерений, распределение которых считают приблизительно нормальным, принимают статистическую модель, приведенную в разделе 5 ГОСТ Р ИСО 5725-1.
1.5 Основной метод, описываемый в настоящем стандарте, предназначен для оценки прецизионности метода измерений:
a) когда требуется найти стандартные отклонения повторяемости и воспроизводимости, определение которых дано в ГОСТ Р ИСО 5725-1;
b) когда предполагаемые к использованию материалы являются однородными либо когда влияние неоднородности может быть учтено в значениях прецизионности;
c) когда приемлемо использование схемы проведения эксперимента, основанной на сбалансированных однородных уровнях.
1.6 Такой же подход может быть использован для предварительной оценки прецизионности методов измерений, которые не стандартизованы или не используются повседневно.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
ГОСТ Р ИСО 5725-4-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений
ГОСТ Р ИСО 5725-5-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
3 Определения
В настоящем стандарте применяют определения, регламентированные ИСО 3534-1 [1] и ГОСТ Р ИСО 5725-1.
Условные обозначения, используемые в ГОСТ Р ИСО 5725, приведены в приложении А.
4 Исходная модель и оцениваемые показатели
4.1 Процедуры, представленные в настоящем стандарте, основываются на статистической модели, приведенной в разделе 5 ГОСТ Р ИСО 5725-1 и, в частности, в равенствах (2) - (6).
Модель описывается следующим выражением
у = т + В + е, (1)
где (для конкретного исследуемого материала, изделия, продукта и т.п.):
т - общее среднее значение (математическое ожидание);
В - лабораторная составляющая систематической погрешности результатов измерений, выполненных в соответствии со стандартным методом в условиях повторяемости;
е - случайная погрешность, имеющая место при каждом измерении в условиях повторяемости.
4.2 Равенства (2) - (6) раздела 5 ГОСТ Р ИСО 5725-1 относятся к истинным стандартным отклонениям рассматриваемых совокупностей. На практике точные значения стандартных отклонений неизвестны, и оценки значений прецизионности должны быть сделаны на основании относительно небольшой выборки из всех возможных лабораторий, а в пределах данных лабораторий - на основании небольшой выборки из всех возможных результатов измерений.
4.3 В статистической практике, когда истинное значение стандартного отклонения s неизвестно и заменяется оценкой, основанной на выборке, символ s заменяется на s, чтобы подчеркнуть, что это - оценка. Это должно быть сделано в каждом из равенств (2) - (6) ГОСТ Р ИСО 5725-1, где:
- оценка межлабораторной дисперсии;
- оценка внутрилабораторной дисперсии;
- среднее арифметическое значение случайной величины , являющееся также оценкой дисперсии повторяемости (сходимости); данное среднее арифметическое значение берется по всем лабораториям, принимающим участие в эксперименте по оценке точности, которые остались после исключения выбросов;
- оценка дисперсии воспроизводимости
(1)
5 Требования к эксперименту по оценке прецизионности
5.1 Программа эксперимента
5.1.1 Согласно программе, используемой в основном методе, пробы (образцы) из q партий материалов, представляющих q различных уровней измеряемой характеристики, посылаются в р лабораторий, каждая из которых в условиях повторяемости на каждом из q уровней получает точно п параллельных определений. Эксперимент данного типа носит название сбалансированного эксперимента с однородными уровнями.
5.1.2 Выполнение измерений должно быть организовано с соблюдением следующих требований.
a) Любая предварительная проверка оборудования должна соответствовать требованиям стандарта на метод измерений.
b) Каждая группа из п измерений, относящихся к одному уровню, должна осуществляться при соблюдении условий повторяемости, т. е в пределах короткого интервала времени и одним и тем же оператором, а также без какой бы то ни было промежуточной перекалибровки аппаратуры, если только это не является неотъемлемой частью выполнения измерений.
c) Необходимо, чтобы группа из п измерений в условиях повторяемости выполнялась независимым образом так, как если бы это были п измерений на различных материалах. Тем не менее, как правило, оператор знает, что он исследует идентичный материал, и поэтому в инструкциях необходимо подчеркнуть, что главной целью эксперимента является определение именно различий (расхождений) в результатах, которые могут появиться при реальных испытаниях. Если же есть основания опасаться, что, несмотря на данное предостережение, предварительные результаты могут повлиять на последующие результаты измерений и, следовательно, на дисперсию повторяемости, то следует принять решение, включать ли в число п на каждом из q уровней некоторое количество проб (образцов) из других уровней, так чтобы оператор не знал, какие из них являются повторами для данного уровня (модифицировав таким перемешиванием основной метод). Такая методика, однако, могла бы создать трудности в обеспечении условий повторяемости в период между измерениями, т.к. в этом случае необходимо, чтобы все q групп из п измерений были осуществлены в пределах короткого интервала времени.
d) Однако при использовании основного метода «в чистом виде» не обязательно стремиться к тому, чтобы все q групп из п измерений были проведены в пределах короткого интервала времени; различные группы измерений могут проводиться в разные дни.
e) Измерения для всех q уровней должны выполняться одним и тем же оператором, и, кроме того, п измерений на данном уровне должны выполняться с использованием одного и того же оборудования.
f) Если в процессе измерений оператор не сможет их выполнить полностью, измерения может завершить другой оператор при условии, что замена оператора не произойдет в пределах группы из п измерений на одном уровне, т.е. замены операторов могут происходить лишь при переходе от одного уровня к другому. Любое такого рода изменение должно регистрироваться вместе с результатами.
g) Должен быть задан временной интервал проведения измерений, т.е. время между датой получения проб и датой завершения всех измерений.
h) Все пробы должны быть отчетливо промаркированы с указанием названия эксперимента и шифра пробы.
5.1.3 В 5.1.2 и других пунктах настоящего стандарта упоминается оператор. В действительности некоторые измерения может проводить группа операторов, каждый из которых выполняет какую-то специфическую часть процедуры. В этом случае группа должна рассматриваться как «оператор», и любое изменение в группе должно восприниматься как смена «оператора».
5.1.4 В коммерческой практике (торговле) результаты измерений (испытаний) могут округляться довольно грубо, однако в эксперименте по оценке прецизионности результаты должны регистрироваться (вычисляться) с точностью, по меньшей мере на один знак большей, чем количество значащих цифр, установленное для регистрации результатов измерений (испытаний) стандартным методом. Если метод не устанавливает количество значащих цифр, округление не должно быть грубее половины оценки стандартного отклонения повторяемости. Когда прецизионность зависит от уровня т, для различных уровней могут потребоваться различные степени округления.
5.2. Привлечение лабораторий
5.2.1 Основные принципы, касающиеся привлечения лабораторий к участию в межлабораторном эксперименте, изложены в 6.3 ГОСТ Р ИСО 5725-1. При привлечении к совместной работе необходимого числа лабораторий должны быть четко сформулированы сферы их ответственности. Пример опросного листа представлен на рисунке 1.
5.2.2 В настоящем стандарте под «лабораторией» подразумевают сочетание таких факторов, как оператор, оборудование и место выполнения измерений (испытаний). Одно место выполнения измерений (испытаний) (или лаборатория в общепринятом значении этого слова) может, таким образом, представлять собой несколько «лабораторий» в том случае, если оно может предусматривать наличие нескольких операторов, каждый из которых располагает своим рабочим местом с комплектом оборудования и условиями, в которых должна выполняться работа.
Рисунок 1 - Опросный лист для межлабораторного исследования
5.3 Подготовка материалов
5.3.1 Вопросы, которые следует принять во внимание при отборе материалов, предназначенных для использования в эксперименте по оценке прецизионности, рассмотрены в 6.4 ГОСТ Р ИСО 5725-1.
5.3.2 При решении вопроса по обеспечению материалом для проведения эксперимента необходимо иметь в виду возможность его случайных потерь или ошибок при получении некоторых результатов измерений, что может потребовать использование дополнительного количества материала. Материала должно быть достаточно, чтобы обеспечить эксперимент и предусмотреть соответствующий резерв.
5.3.3 Необходимо рассмотреть, желательно ли для некоторых лабораторий получение каких-либо предварительных результатов измерений с целью ознакомления с методом измерений перед получением официального результата измерений и если да, то должен ли быть предусмотрен для данной цели дополнительный материал (не из числа проб для эксперимента по оценке прецизионности).
5.3.4 При необходимости гомогенизация материала должна быть проведена наиболее подходящим для него способом. Если материал, предназначенный для испытаний, не является однородным, важно подготовить пробы тем способом, который установлен для метода, предпочтительно начав с одной партии реального материала для каждого уровня. Для нестабильных материалов должны быть даны специальные указания по их хранению и обращению с ними.
5.3.5 Для проб на каждом уровне в каждой лаборатории должны использоваться п отдельных контейнеров в случае, если существует хотя бы малейшая опасность ухудшения качества материалов после того, как контейнер один раз уже был открыт (например, за счет окисления, потери летучих компонентов или в случае гигроскопического материала). Для нестабильных материалов должны быть даны специальные указания по их хранению и обращению с ними. Могут также понадобиться меры предосторожности для обеспечения идентичности проб вплоть до момента проведения измерений. Если материал, предназначенный для измерений, состоит из смеси порошков с различной относительной плотностью или зернистостью, может потребоваться определенная осторожность, так как вследствие сотрясения может произойти расслоение, например во время транспортирования. В случаях возможной реакции при контакте с атмосферой пробу нужно плотно упаковать в ампулы - либо вакуумированные, либо заполненные инертным газом. Для скоропортящихся материалов, таких как пробы пищи или крови, при необходимости может потребоваться направлять их в лаборатории, участвующие в эксперименте, в глубокозамороженном состоянии, с подробными инструкциями относительно процедуры оттаивания.
6 Персонал, привлекаемый к участию в эксперименте по оценке прецизионности
Примечание 3 - Нельзя ожидать, что методы работы различных лабораторий будут идентичными. Следовательно, содержание настоящего раздела является лишь руководством, которое нужно модифицировать применительно к каждой конкретной ситуации.
6.1 Совет экспертов
6.1.1 Совет должен состоять из экспертов, хорошо знакомых с методом измерений и его применением.
6.1.2 Задачами совета экспертов являются:
a) планирование и координация эксперимента;
b) принятие решения по вопросам количества лабораторий, уровней и измерений, предполагаемых к проведению, а также количества требуемых значащих цифр;
c) назначение лица, ответственного за статистическую обработку данных эксперимента (см. 6.2);
d) назначение лица, ответственного за проведение эксперимента (см. 6.3);
e) рассмотрение и обсуждение инструкций, которые должны быть представлены инспектором лабораторий в дополнение к стандартному методу измерений;
f) принятие решения по вопросу, могут ли некоторые операторы быть допущены к проведению небольшого количества неофициальных измерений для того, чтобы восстановить навыки владения методом после долгого перерыва (такие измерения ни в коем случае не должны осуществляться на официальных совместных пробах);
g) обсуждение доклада о результатах статистического анализа, полученных по завершении эксперимента;
h) установление окончательных значений для стандартных отклонений повторяемости и воспроизводимости;
i) принятие решений в случаях, когда требуются дальнейшие действия с целью совершенствования стандарта на метод измерений, либо в отношении тех лабораторий, чьи результаты измерений были исключены как выбросы.
6.2 Статистические функции
По крайней мере один член совета экспертов должен иметь опыт статистического планирования и анализа экспериментов. Задачами этого эксперта являются:
a) использование своих специализированных знаний при планировании эксперимента;
b) анализ данных;
c) подготовка доклада для представления совету экспертов с соблюдением указаний, содержащихся в 7.7.
6.3 Исполнительные функции
6.3.1 Обязанности по организации эксперимента как такового должны быть возложены на отдельную лабораторию. Сотрудник данной лаборатории, называемый ответственным исполнителем и назначаемый советом экспертов, должен взять на себя организацию эксперимента.
6.3.2 Задачи ответственного исполнителя:
a) привлечь к сотрудничеству необходимое количество лабораторий и обеспечить назначение инспекторов;
b) организовать и проверить подготовку материалов и отправку проб; для каждого уровня необходимое количество материала должно быть выделено и храниться в качестве резерва;
c) подготовить инструкции, распространяющиеся на требования пункта 5.1.2, и заблаговременно разослать их инспекторам с тем, чтобы у них была возможность представить какие-либо комментарии или вопросы и обеспечить правильный отбор операторов (см. 6.4.2а);
d) разработать удобные формы: для оператора с целью их заполнения в качестве рабочих документов, для инспектора - в виде протокола результатов испытаний в необходимом формате по количеству значащих цифр (такие формы должны включать в себя фамилию оператора, даты получения и измерения проб, используемое оборудование и другую имеющую отношение к делу информацию);
e) рассматривать любые вопросы, поступившие от лабораторий и имеющие отношение к выполнению измерений;
f) следить за соблюдением общего временного графика выполнения работ;
g) обеспечить сбор форм с данными и передачу их эксперту по статистике.
6.4 Инспекторы
6.4.1 Один из сотрудников каждой из участвующих в эксперименте лабораторий должен быть назначен ответственным за организацию фактического выполнения измерений в соответствии с инструкциями, полученными от ответственного исполнителя, а также за подготовку отчетности о результатах измерений (испытаний).
6.4.2 Задачи инспектора:
a) обеспечить правильный отбор операторов (ими должны быть лица, которые могли бы нормально выполнять такого рода измерения в повседневной работе);
b) выдавать пробы операторам в соответствии с указаниями ответственного исполнителя (а также, в случае необходимости, обеспечивать материалом для ознакомительных экспериментов);
c) инспектировать выполнение измерений (инспектор не должен принимать участия в осуществлении процедуры выполнения измерений);
d) обеспечить выполнение требуемого количества измерений;
e) обеспечить соблюдение установленного расписания выполнения измерений;
f) обеспечить сбор результатов измерений, регистрируемых в согласованном формате по количеству десятичных знаков, с описанием любых аномалий и трудностей, с которыми пришлось столкнуться, а также комментариев операторов.
6.4.3 Инспектор каждой лаборатории должен составить полный отчет, содержащий:
а) результаты измерений, разборчиво заносимые операторами в предусмотренные формы, без переписывания от руки или печатания (в качестве альтернативы допускается распечатка с компьютера или испытательного оборудования);
b) исходные данные наблюдений или показания (если таковые имеются), на основании которых были получены результаты измерений, разборчиво заносимые оператором в предусмотренные формы, без переписывания от руки или печатания;
c) комментарии (замечания) операторов по стандарту на метод измерений;
d) сведения о нарушениях или помехах, если таковые были во время измерений, включая любую смену оператора, которая могла быть вместе с данными о том, какие измерения каким оператором были выполнены, и причины, приведшие к любым пропускам в получении результатов;
e) дата(ы) получения пробы;
f) дата(ы), когда каждая из проб была подвергнута измерениям;
g) информация об используемом оборудовании;
h) иные сведения, имеющие отношение к делу.
6.5 Операторы
6.5.1 В каждой лаборатории измерения должны осуществляться одним оператором, отобранным в качестве ответственного за выполнение измерений в процессе нормальной работы.
6.5.2 Поскольку предметом эксперимента является определение прецизионности, достигаемое совместно всеми операторами, реализующими стандартный метод измерений, операторы вообще не должны получать каких-либо указаний по расширению (модификации) стандарта на метод измерений (далее - стандарт). Однако внимание операторов должно быть обращено на то, что целью эксперимента является нахождение пределов, в которых результаты могут варьироваться на практике, чтобы у них было меньше соблазнов для исключения или доработки тех результатов, которые им кажутся несостоятельными.
6.5.3 Хотя, как правило, операторы не должны получать никаких дополнительных разъяснений к стандартному методу измерений, они должны привлекаться к обсуждению стандарта и, в особенности, к подтверждению достаточности, недвусмысленности и ясности содержащихся в нем указаний.
6.5.4 Задачи операторов:
a) выполнять измерения в соответствии со стандартным методом измерений;
b) сообщать о любых аномалиях или трудностях, с которыми пришлось столкнуться; лучше сообщить об ошибке, чем подгонять результаты измерений, так как один или два недостающих результата не испортят эксперимента, а большое их количество выявит недостаток стандарта;
c) комментировать адекватность указаний, содержащихся в стандарте; операторы должны сообщать о любых случаях, когда они не в состоянии следовать указаниям, так как это также может выявить недостаток, присущий стандарту.
7 Статистический анализ данных эксперимента по оценке прецизионности
7.1 Предварительные соображения
7.1.1 Анализ данных как статистическая задача, решаемая экспертом по статистике, предусматривает три следующих один за другим этапа:
a) критическое изучение данных с целью обнаружения и обработки выбросов и других нерегулярностей, а также проверки пригодности модели;
b) расчет предварительных оценок прецизионности и средних значений для каждого уровня раздельно;
c) установление окончательных значений прецизионности и средних значений, в том числе аналитическое представление зависимости между прецизионностью и средним значением т для уровня - в случаях, когда анализ показывает, что такая зависимость существует.
7.1.2 При анализе в первую очередь рассчитывают для каждого уровня раздельно оценки:
- дисперсии повторяемости
- межлабораторной дисперсии
- дисперсии воспроизводимости
- среднего значения т.
7.1.3 Что касается выбросов, анализ включает в себя систематическое использование статистических приемов (тестов), большое многообразие которых представлено в технической литературе, и которые могли бы быть применены в настоящем стандарте. Из практических соображений в стандарт было включено лишь ограниченное количество таких приемов, описанных в 7.3.
7.2 Представление результатов и используемые обозначения
7.2.1 Базовые элементы
Каждое сочетание лаборатории и уровня (определенного образца материала) носит название базового элемента (ячейки) эксперимента по оценке прецизионности. В идеальном случае результаты эксперимента с р лабораториями и q уровнями представляют собой таблицу с pq базовыми элементами, каждый из которых содержит п результатов измерений, которые в совокупности могут быть использованы для расчета стандартных отклонений повторяемости и воспроизводимости. Данная идеальная ситуация, однако, не всегда достигается на практике. Отклонения происходят вследствие избыточных данных, недостающих данных и выбросов.
7.2.2 Избыточные данные
Иногда лаборатория может осуществить и запротоколировать более чем п официально заданных результатов измерений. В таком случае инспектор должен сообщить, почему это было сделано и какие результаты измерений являются корректными. Если объяснение заключается в том, что все результаты равнозначны, то должен быть произведен случайный отбор из имеющихся в наличии результатов измерений с целью выбора запланированного количества результатов для анализа.
7.2.3 Недостающие данные
В других случаях некоторые из результатов измерений могут отсутствовать, например вследствие потери образца или ошибки при выполнении измерения. По результатам анализа, рекомендованного в 7.1, совершенно незаполненными базовыми элементами можно просто пренебречь, в то время как частично незанятые базовые элементы могут быть учтены в стандартной процедуре расчета.
7.2.4 Выбросы
Это данные среди исходных результатов измерений (или данные, занесенные в таблицу и полученные из результатов измерений), которые настолько отклоняются от сопоставимых данных, внесенных в ту же самую таблицу, что признаются несовместимыми. Опыт показал, что невозможно во всех случаях избежать выбросов, и с ними нужно поступать таким же образом, как с недостающими данными.
7.2.5 Выпадающие лаборатории
Когда на различных уровнях в пределах одной и той же лаборатории имеет место несколько необъяснимых аномальных результатов измерений, данная лаборатория может рассматриваться как выброс, имеющий слишком высокую внутрилабораторную дисперсию и/или слишком большую внутрилабораторную систематическую погрешность. В таком случае может оказаться целесообразным исключить некоторые или все данные такой выпадающей лаборатории.
Настоящий стандарт не содержит статистических тестов, при помощи которых может быть сделан вывод относительно сомнительных лабораторий. Ответственность за первоначальное решение должна возлагаться на эксперта по статистике, однако обо всех отбракованных лабораториях необходимо сообщать совету экспертов для принятия решения о дальнейших действиях.
7.2.6 Ошибочные данные
Явно ошибочные данные должны быть изучены и исправлены или исключены.
7.2.7 Результаты измерений, сбалансированных по однородным уровням
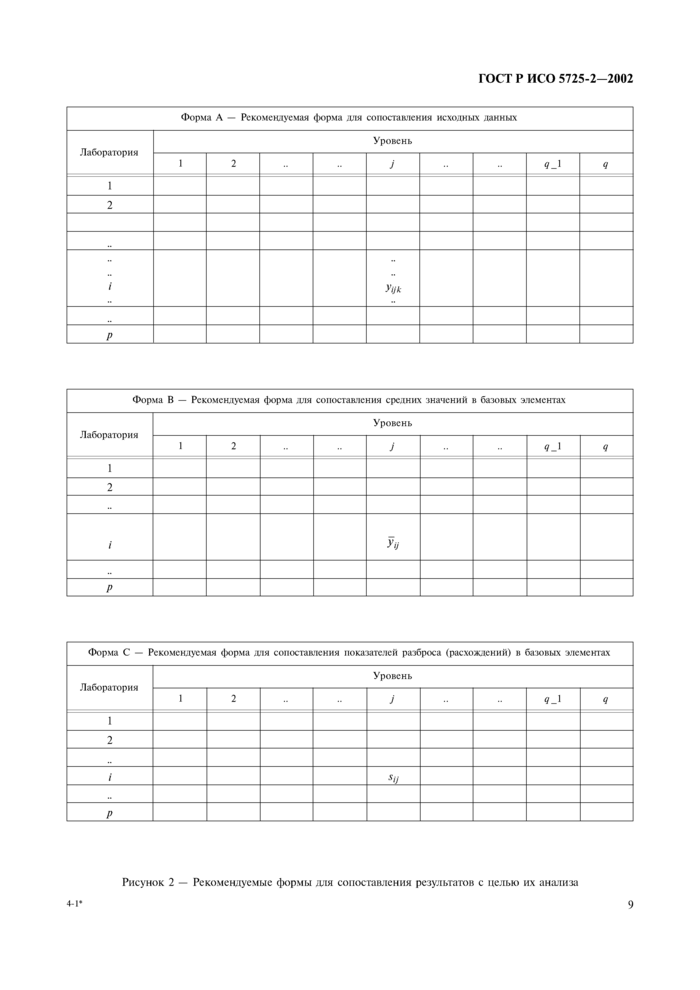
Идеальный случай представляет собой р лабораторий с номерами i (i = 1, 2, ..., р), каждая из которых проводит измерения на q уровнях с номерами j (j = 1, 2, ..., q), осуществляя п параллельных определений на каждом уровне (каждая ij комбинация). В итоге представляют pqn результатов измерений. Вследствие появления недостающих (7.2.3) или отклоняющихся (7.2.4) результатов измерений, или же выпадающих лабораторий (7.2.5), или ошибочных данных (7.2.6) эта идеальная ситуация не всегда достижима. Поэтому формы записи, приведенные в 7.2.8 - 7.2.10, а также процедуры, представленные в 7.4, приемлемы для различного количества результатов измерений. Рекомендуемые формы для статистического анализа представлены на рисунке 2. Для удобства они будут упоминаться просто как формы А, В и С.
|
Форма А - Рекомендуемая форма для сопоставления исходных данных |
|||||||||
|
Лаборатория |
Уровень |
||||||||
|
1 |
2 |
... |
... |
j |
... |
... |
q - 1 |
q |
|
|
1 |
|||||||||
|
2 |
|||||||||
|
... |
|||||||||
|
... ... i ... |
... ... yijk ... |
||||||||
|
... |
|||||||||
|
p |
|||||||||
|
Форма В - Рекомендуемая форма для сопоставления средних значений в базовых элементах |
|||||||||
|
Лаборатория |
Уровень |
||||||||
|
1 |
2 |
... |
... |
j |
... |
... |
q - 1 |
q |
|
|
1 |
|||||||||
|
2 |
|||||||||
|
... |
|||||||||
|
i |
|
||||||||
|
... |
|||||||||
|
p |
|||||||||
|
Форма С - Рекомендуемая форма для сопоставления показателей разброса (расхождений) в базовых элементах |
|||||||||
|
Лаборатория |
Уровень |
||||||||
|
1 |
2 |
... |
... |
j |
... |
... |
q - 1 |
q |
|
|
1 |
|||||||||
|
2 |
|||||||||
|
... |
|||||||||
|
i |
sij |
||||||||
|
... |
|||||||||
|
p |
|||||||||
Рисунок 2 - Рекомендуемые формы для сопоставления результатов с целью их анализа
7.2.8 Исходные результаты измерений
См. форму А на рисунке 2,
где nij - количество результатов измерений в базовом элементе (ячейке) для лаборатории i на уровне j;
yijk - любой из этих результатов измерений (k = 1, 2, ..., пij);
pj - количество лабораторий, отчитавшихся по крайней мере одним результатом измерений для уровня j (после исключения результатов, признанных выбросами или ошибочными).
7.2.9 Средние значения в базовых элементах (форма В на рисунке 2)
Рассчитывают по данным формы А следующим образом
(2)
Средние значения для базовых элементов необходимо фиксировать с точностью, на одну значащую цифру большей, чем результаты испытаний в форме А.
7.2.10 Показатели разброса (расхождения) в базовых элементах (форма С на рисунке 2).
Рассчитывают по данным форм А (см. 7.2.8) и В (7.2.9) следующим образом. В общем случае в качестве таких показателей используют значения внутриэлементных стандартных отклонений, рассчитываемые на основе данных форм А и В по формуле
(3)
или по эквивалентной формуле
(4)
При использовании формул (3) и (4) необходимо сохранять достаточное количество значащих цифр при расчетах, а именно каждое промежуточное значение должно рассчитываться с количеством значащих цифр, по крайней мере вдвое большим по сравнению с количеством цифр в исходных данных.
Примечание 4 - Если базовый элемент ij содержит лишь два результата измерений, то внутриэлементное расхождение (аналог стандартного отклонения) равно
sij = ÷yij1 - yij2÷/√2. (5)
Таким образом, если во всех базовых элементах содержится по два результата измерений, для простоты вместо стандартных отклонений могут быть использованы абсолютные расхождения.
Стандартное отклонение должно выражаться значением, на одну значащую цифру большим, чем в результатах по форме А.
Для значений nij, меньших 2, в форме С должен быть проставлен прочерк.
7.2.11 Исправленные или исключенные данные
Поскольку некоторые из данных могут быть исправлены или исключены на основании тестов, описанных в 7.1.3, 7.3.3 и 7.3.4, значения уijk, пij и рj, используемые для окончательного определения прецизионности и общего среднего, могут отличаться от значений, соответствующих исходным результатам измерений, зафиксированным в формах А, В и С (рисунок 2). Следовательно, при представлении в отчете (докладе) окончательных значений прецизионности и правильности необходимо всегда точно определять, какие данные, если таковые имеются, были исправлены или исключены.
7.3 Анализ данных на совместимость и наличие выбросов
См. стандарт ASTM Е 691-87 [2].
Исходя из данных, собранных на различных уровнях, нужно оценить стандартные отклонения повторяемости и воспроизводимости. Наличие отдельных лабораторий или значений, которые представляются несовместимыми со всеми остальными лабораториями или значениями, может изменить оценки, так что решения об исключении данных нужно принимать только после тщательного анализа. Вводят два подхода к принятию таких решений:
a) графический анализ совместимости;
b) статистическое тестирование выбросов.
7.3.1 Графический анализ совместимости
Используют две меры, носящие названия статистик Манделя h и k. Можно отметить, что помимо отображения вариабельности (непостоянства результатов) метода измерений, они помогают оценить лаборатории.
7.3.1.1 Сначала для каждой лаборатории рассчитывают статистики межлабораторной совместимости h посредством деления средних различий в базовых элементах (среднее значение для базового элемента минус общее среднее значение для данного уровня) на стандартные отклонения средних значений в базовых элементах (для данного уровня)
(6)
где определены в 7.2.9, а - в 7.4.4.
Затем значения hij для каждого базового элемента наносят на диаграмму в последовательности увеличения индекса i, так чтобы каждому номеру лаборатории соответствовала группа значений hij, относящихся к разным уровням (см. рисунок В.7).
7.3.1.2 Далее рассчитывают статистики внутрилабораторной совместимости k путем вычисления внутриэлементного стандартного отклонения
для каждого уровня и последующего вычисления значений
(7)
для каждой лаборатории в пределах каждого уровня.
Наконец значения kij для каждого базового элемента наносят на диаграмму в последовательности увеличения индекса i, так чтобы каждому номеру лаборатории соответствовала группа значений kij, относящихся к разным уровням (см. рисунок В.8).
7.3.1.3 Изучая диаграммы для h и k, можно отметить, что наглядные представления результатов для отдельных лабораторий заметно отличаются от других. Это выражается в последовательно высокой или низкой внутриэлементной вариации и/или в последовательно высоких или низких средних значениях для базовых элементов по многим уровням. С такими лабораториями нужно установить контакт, чтобы постараться выяснить причину расхождений.
На основании полученных сведений эксперт по статистике может:
a) сохранить на данный момент результаты лаборатории;
b) попросить лабораторию выполнить измерение заново (если это возможно);
c) исключить данные лаборатории из анализа.
7.3.1.4 В диаграммах для h можно увидеть различные проявления. В одном случае все лаборатории могут иметь как положительные, так и отрицательные значения h на различных уровнях эксперимента. В другом случае отдельные лаборатории могут иметь тенденцию к представлению либо только положительных, либо только отрицательных значений h, и количество лабораторий, дающих отрицательные значения, приблизительно равно количеству лабораторий, дающих положительные значения. Ни одно из этих проявлений не является необычным или требующим изучения, хотя во втором случае может возникнуть мысль о существовании в лаборатории некоего общего источника систематической погрешности. Однако если все значения h для одной лаборатории имеют один знак, а для прочих лабораторий - другой, то в этом случае необходимо попытаться найти причину. Также нужно искать причины расхождений, если значения h для лаборатории, во-первых, являются сравнительно большими и, во-вторых, неким систематическим образом зависят от уровня эксперимента. На диаграммах для h проводят линии, соответствующие индикаторам, представленным в 8.3 (таблицы 6 и 7). Эти индикаторные линии служат ориентирами при анализе диаграмм.
7.3.1.5 Если одна из лабораторий выделяется по статистике k, имея при этом много больших значений, то должна быть установлена причина этого, указывающая на худшую повторяемость по сравнению с другими лабораториями. Например, лаборатория могла бы иметь последовательно меньшие значения k, если бы не влияли такие факторы, как завышение при округлении своих данных или недостаточная чувствительность в диапазоне измерений. На диаграммах для k также проводятся линии в соответствии с индикаторами, представленными в 8.3 (таблицы 6 и 7), служащие ориентирами при анализе диаграмм.
7.3.1.6 Когда из части диаграммы для h или k, относящейся к некоей лаборатории, видно, что некоторые значения близки к критическим, т.е. соответствующим индикаторным линиям, нужно рассмотреть всю диаграмму для уровня. Нередко значение, представляющее большим в части диаграммы, относящейся к лаборатории, оказывается в разумных пределах совместимым со значениями для других лабораторий на том же уровне. Однако если обнаруживается, что оно сильно отличается от значений для других лабораторий, то необходимо попытаться выяснить причину.
7.3.1.7 В дополнение к диаграммам h и k гистограммы средних значений и расхождений для базовых элементов могут показать наличие, например, двух несовпадающих подмножеств результатов измерений. Такой случай потребовал бы специального подхода, поскольку общий основной принцип, лежащий в основе методов, описываемых здесь, предполагает единственное множество с унимодальным распределением.
7.3.2 Статистическое тестирование выбросов
7.3.2.1 Для анализа данных на наличие выбросов рекомендуется следующая методика.
a) Для идентификации выбросов применяют критерии, приведенные в 7.3.3 и 7.3.4:
- если значение меры, определяемой статистическим критерием (значением тестовой статистики), меньше (или равно) 5 %-ного критического значения тестовой статистики (критического значения при 5 %-ном уровне значимости), то тестируемую позицию признают корректной;
- если значение тестовой статистики больше 5 %-ного критического значения и меньше (или равно) 1 %-ного критического значения, то тестируемую позицию называют квазивыбросом и отмечают одной звездочкой;
- если значение тестовой статистики больше 1 %-ного критического значения, то тестируемую позицию называют статистическим выбросом и отмечают двумя звездочками.
b) Далее проводят исследование с целью выяснения, могут ли квазивыбросы и/или статистические выбросы быть объяснены какой-либо технической ошибкой, например:
- ошибкой при выполнении измерения;
- ошибкой в расчетах;
- элементарной опиской при переписывании результата измерений;
- анализом не той пробы (образца).
В случае, когда ошибка появилась при расчетах или переписывании, сомнительный результат должен быть заменен правильным значением; когда ошибка являлась следствием анализа не той пробы, результат должен быть помещен в соответствующий ему базовый элемент. После того, как такого рода коррекция будет произведена, исследование на предмет квазивыбросов или выбросов должно быть повторено. В случае, если объяснение технической ошибки таково, что оно свидетельствует о невозможности замены сомнительного результата измерений, он должен быть исключен как «подлинный» выброс, не имеющий отношения к правильно проводимому эксперименту.
c) Когда какие-либо квазивыбросы и/или статистические выбросы остаются необъяснимыми или исключенными в качестве принадлежащих к выпадающей лаборатории, квазивыбросы сохраняют в качестве коррективных позиций, а статистические выбросы исключают, если только эксперт по статистике не решит оставить их, имея на это соответствующие основания.
d) В случае, когда после вышеописанной процедуры данные для базового элемента были исключены для формы В на рисунке 2, то тогда должны быть также исключены соответствующие данные для формы С на рисунке 2 и наоборот.
7.3.2.2 В 7.3.3 и 7.3.4 представлены два типа критериев. Критерий Кохрена предназначен для обработки внутрилабораторных расхождений результатов измерений и должен применяться в первую очередь, после чего должны быть приняты корректирующие меры, в случае необходимости, с повторением измерений (испытаний). Другой критерий (Граббса) главным образом предназначен для обработки межлабораторных расхождений, а также может использоваться (если п > 2) в случаях, когда проверка с применением критерия Кохрена вызвала подозрение в том, что высокая внутрилабораторная вариация обусловлена только одним из результатов измерений в базовом элементе.
7.3.3 Критерий Кохрена
7.3.3.1 В настоящем стандарте предполагается, что между лабораториями существуют лишь небольшие различия во внутрилабораторных расхождениях. Опыт, однако, показывает, что дело обстоит не всегда так, поэтому для проверки справедливости этого предположения нужна количественная оценка. Для данной цели могли бы быть использованы несколько критериев, но был выбран критерий Кохрена.
7.3.3.2 Для совокупности из р стандартных отклонений si, рассчитанных исходя из одного и того же количества (n) результатов испытаний в базовых элементах, тестовая статистика Кохрена имеет вид
(8)
где smax - наивысшее значение стандартного отклонения в совокупности.
a) В случае, если значение тестовой статистики меньше (или равно) 5 %-ного критического значения, тестируемую позицию признают корректной.
b) В случае, если значение тестовой статистики больше 5 %-ного критического значения и меньше (или равно) 1 %-ного значения, тестируемую позицию называют квазивыбросом и отмечают одной звездочкой.
c) В случае, если значение тестовой статистики больше 1 %-ного критического значения, тестируемую позицию называют статистическим выбросом и отмечают двумя звездочками.
Критические значения для критерия Кохрена представлены в 8.1 (таблица 4).
Критерий Кохрена должен применяться для формы С (рисунок 2) на каждом уровне раздельно.
7.3.3.3 Строго говоря, критерий Кохрена применяют лишь в случаях, когда все стандартные отклонения исходят из одного и того же количества (n) результатов измерений, полученных в условиях повторяемости. В фактических случаях это количество может меняться за счет недостающих или исключенных данных. В настоящем стандарте тем не менее предполагается, что в должным образом организованном эксперименте такие изменения в количестве результатов измерений из расчета на базовый элемент будут ограничены и ими можно пренебречь, то есть критерий Кохрена можно использовать применительно к количеству результатов измерений п, имеющих место в большинстве базовых элементов.
7.3.3.4 При помощи критерия Кохрена проверяют только наивысшее значение в совокупности стандартных отклонений, и поэтому такая проверка является односторонней. Разброс в дисперсиях может также, разумеется, проявляться в наинизших значениях стандартных отклонений. Однако на малые значения стандартного отклонения может оказывать очень сильное влияние степень округления исходных данных, и поэтому они не очень надежны. Кроме того, представляется нецелесообразным отвергать данные лаборатории из-за того, что ею достигнута более высокая прецизионность в результатах измерений по сравнению с другими лабораториями. Поэтому критерий Кохрена считают адекватным.
7.3.3.5 При критическом рассмотрении формы С (рисунок 2) иногда может обнаружиться, что значения стандартных отклонений для определенной лаборатории на всех или на большинстве уровней ниже значений стандартных отклонений для других лабораторий. Это может указывать на то, что лаборатория работает с более низким значением стандартного отклонения повторяемости по сравнению с другими лабораториями, которое, в свою очередь, может быть обусловлено либо лучшей техникой выполнения анализов и лучшим оборудованием, либо модифицированным или неправильным применением стандартного метода измерений. В случае, если это имеет место, об этом необходимо сообщить совету экспертов, который должен решить, заслуживает ли данный вопрос более детального изучения. (Примером этого является лаборатория № 2 в эксперименте, подробно описанном в В.1 приложения В).
7.3.3.6 Если наивысшее значение стандартного отклонения классифицировано как выброс, то оно должно быть исключено, а проверка с использованием критерия Кохрена может быть повторена на оставшихся значениях. Следует заметить, что процедура повторения может привести к излишним исключениям данных в случаях, когда нормальное распределение, принятое за основу, не является достаточно хорошей аппроксимацией. Повторное применение критерия Кохрена предлагается здесь лишь в качестве полезного средства ввиду отсутствия статистического критерия, разработанного для проверки нескольких выбросов вместе. Критерий Кохрена не разрабатывался для данной цели, и выводы при его повторном применении необходимо делать с большой осторожностью. Так же осторожно нужно использовать критерий Кохрена в случаях, когда результаты, характеризующиеся высокими значениями стандартных отклонений (в особенности, если они имеют место в пределах лишь одного из уровней), представлены двумя или тремя лабораториями. С другой стороны, если на различных уровнях в пределах одной лаборатории обнаруживается несколько квазивыбросов и/или статистических выбросов, то это может быть веским указанием на то, что внутрилабораторная дисперсия слишком высока, и данные этой лаборатории должны быть полностью исключены.
7.3.4 Критерий Граббса
7.3.4.1 Проверка на один выброс
Для проверки, не является ли выбросом наибольшая величина из х расположенных в порядке возрастания совокупности данных xi (i = 1, 2, ..., р), вычисляют статистику Граббса Gp по формуле
(9)
где
(10)
(11)
Для проверки значимости наименьшего результата наблюдения вычисляют тестовую статистику
a) В случае, если значение тестовой статистики меньше (или равно) 5 %-ного критического значения, тестируемую позицию признают корректной.
b) В случае, если значение тестовой статистики больше 5 %-ного критического значения и меньше (или равно) 1 %-ного критического значения, тестируемую позицию называют квазивыбросом и отмечают одной звездочкой.
c) В случае, если значение тестовой статистики больше 1 %-ного критического значения, тестируемую позицию называют статистическим выбросом и отмечают двумя звездочками.
7.3.4.2 Проверка на два выброса
Чтобы проверить, могут ли два наибольших результата наблюдений быть выбросами, вычисляют статистику Граббса
(12)
где
(13)
(14)
а также
(15)
Соответственно, чтобы проверить два наименьших результата наблюдений, вычисляют статистику Граббса
(16)
где
(17)
(18)
Критические значения для критерия Граббса представлены в 8.2 (таблица 5).
7.3.4.3 Применение критерия Граббса
При анализе эксперимента по оценке прецизионности критерий Граббса может быть применен к следующим случаям.
a) Анализ средних значений базовых элементов (форма В на рисунке 2) для заданного уровня j, при этом
и
p = pj.
Сначала к средним значениям базовых элементов уровня j применяют критерий Граббса для одного выброса, как описано в 7.3.4.1. Если обнаруживается, что среднее значение базового элемента является выбросом, необходимо исключить его и повторить проверку для другого экстремального среднего значения базового элемента (например, если наивысшее значение является выбросом, то тогда следует проверить наинизшее значение, а наивысшее значение при этом исключить), однако при этом не следует применять критерий Граббса для двух выбросов, описанный в 7.3.4.2. Этот последний критерий нужно применять в случае, если при проверке с использованием критерия Граббса для одного выброса обнаруживается, что средние значения базовых элементов не имеют выбросов.
b) Анализ исходных данных в пределах базового элемента, для которого в результате проверки с использованием критерия Кохрена обнаруживается сомнительность значения стандартного отклонения.
7.4 Расчет общего среднего значения и дисперсий
7.4.1 Метод анализа
Метод анализа, принятый в настоящем стандарте, включает в себя нахождение оценки общего среднего т и прецизионности для каждого уровня отдельно. Результаты расчета представляют в виде таблицы для каждого значения j.
7.4.2 Исходные данные
Исходные данные, необходимые для расчетов, должны быть представлены в трех таблицах (рисунок 2), соответствующих формам:
- таблице А, содержащей результаты измерений;
- таблице В, содержащей средние значения в базовых элементах;
- таблице С, содержащей показатели разброса (расхождений) в базовых элементах.
7.4.3 Непустые базовые элементы
Следствием правила, сформулированного в 7.3.2.1d, является то, что количество непустых базовых элементов для каждого уровня, используемых при расчете, в таблицах В и С всегда будет одинаковым. Исключение мог бы составить случай, когда, вследствие недостающих данных, базовый элемент в таблице А содержит лишь один результат измерений, что повлечет за собой появление незаполненного базового элемента в таблице С, но не в таблице В. В данном случае можно:
a) отбросить единичный результат измерений, после чего появятся незаполненные базовые элементы в таблицах В и С, или
b) если потерю информации рассматривают как нежелательную, вносят прочерк в форму С.
Количество непустых базовых элементов может быть разным для различных уровней, поэтому и введен индекс j в pj.
7.4.4 Расчет общего среднего значения
Для уровня j общее среднее значение равно
(19)
7.4.5 Расчет дисперсий
Для каждого уровня рассчитывают три дисперсии: повторяемости, межлабораторную и воспроизводимости.
7.4.5.1 Дисперсия повторяемости равна
(20)
7.4.5.2 Межлабораторная дисперсия равна
(21)
где
(22)
(23)
Соответствующие расчеты проиллюстрированы примерами в В.1 и В.3 приложения В.
7.4.5.3 Для частного случая, когда все пij = п = 2, приведенные формулы упрощаются и имеют вид
Они проиллюстрированы примером, представленным в В.2 приложения В.
7.4.5.4 Когда вследствие случайных эффектов (вызванных ограниченностью выборки) из данных расчетов для получается отрицательное значение, его следует принять равным нулю.
7.4.5.5 Дисперсия воспроизводимости составит
(24)
7.4.6 Зависимость дисперсий от т
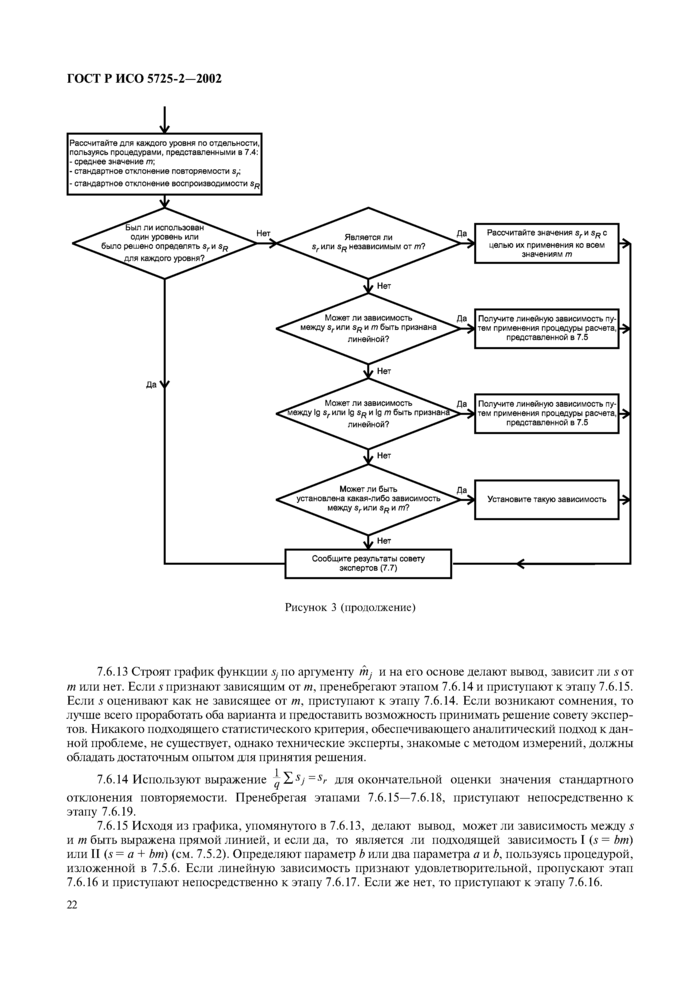
Далее необходимо определить, зависит ли прецизионность от общего среднего значения т для уровня, и если зависит, то найти соответствующее функциональное соотношение.
7.5 Установление функциональной зависимости между значениями прецизионности и средним значением т для уровня
7.5.1 Регулярная функциональная связь между прецизионностью и т существует не во всех случаях. В частности, если неотъемлемой частью расхождений между результатами измерений является неоднородность материала, функциональная связь будет иметь место лишь в случае, если данная неоднородность является регулярной функцией среднего значения для уровня т. Для твердых материалов различного состава, получаемых по различным технологиям, эта функциональная связь никоим образом не является несомненной. Этот вопрос нужно решить до применения описанной ниже процедуры. В качестве альтернативы для каждого рассматриваемого материала могли бы быть установлены отдельные значения прецизионности.
7.5.2 Обоснования и процедуры вычислений, изложенные в 7.5.3 - 7.5.9, относятся к стандартным отклонениям как повторяемости, так и воспроизводимости, однако для краткости здесь они представлены только для повторяемости. Будут рассмотрены только три типа соотношений:
I: sr = bm (прямая линия, проходящая через начало координат);
II: sr = a + bm (прямая линия, проходящая выше начала координат);
III: lgsr = с + dlgm (или sr = Cmd); d £ 1 (экспоненциальная зависимость).
Можно ожидать, что в большинстве случаев существования зависимости по крайней мере одно из данных равенств даст ее удовлетворительное описание. Если же нет, то эксперт по статистике, осуществляющий анализ, должен будет найти альтернативное решение. Чтобы избежать путаницы, постоянные величины а, b, с, С и d, присутствующие в данных равенствах, могут различаться при помощи подстрочных индексов ar, br для повторяемости и aR, bR - для воспроизводимости, однако они были опущены в записи в данном разделе опять же для упрощения системы обозначений. Кроме того, sr было сокращено просто до s для удобства простановки подстрочного индекса уровня j.
7.5.3 Обычно d > 0, таким образом, зависимости I и III будут сводиться к s = 0 для т = 0, что может показаться неприемлемым. Однако при упоминании в отчетах данных по прецизионности необходимо разъяснять, что они применимы только в пределах уровней, охватываемых межлабораторным экспериментом по ее оценке.
7.5.4 Для а = 0 и d = 1 все три зависимости являются тождественными, поэтому в случае, когда а располагается вблизи нуля и/или d располагается вблизи единицы, две или все три данные зависимости будут обеспечивать практически равноценное соответствие; предпочтение должно быть отдано зависимости I, поскольку она допускает нижеследующее простое утверждение: «Два результата измерений считаются сомнительными, если они различаются более чем на (100b) %».
С точки зрения статистической терминологии данная формулировка означает, что коэффициент вариации (100s/m) постоянен для всех уровней.
7.5.5 Если на графике функции sj в зависимости от аргумента или на графике функции lgsj в зависимости от аргумента обнаруживается, что совокупность точек лежит достаточно близко к прямой линии, то может оказаться достаточной графическая аппроксимация; однако если из каких-то соображений предпочтение отдается аналитическому методу аппроксимации, то для зависимостей I и II рекомендуется методика, изложенная в 7.5.6, а для зависимости III - методика, представленная в 7.5.8.
7.5.6 С точки зрения статистики аппроксимация прямой линией осложняется за счет того, что как , так и sj являются оценками и, следовательно, подвержены ошибкам. Однако поскольку угловой коэффициент b обычно невелик (порядка 0,1 или менее), то ошибки в оценке имеют небольшое влияние, и превалируют ошибки в оценке s.
7.5.6.1 Хорошая оценка параметров линии регрессии требует взвешенной регрессии, так как стандартное отклонение величины s пропорционально прогнозируемому значению sj ().
Весовые коэффициенты должны быть пропорциональны 1/()2, где представляет собой прогнозируемое стандартное отклонение повторяемости для уровня j. Однако зависит и от параметров, которые еще только должны быть рассчитаны.
Математически правильная методика нахождения оценок, соответствующих наименьшим взвешенным среднеквадратичным отклонениям, довольно сложна. Рекомендуется нижеследующая методика, которая оказалась удовлетворительной на практике.
7.5.6.2 При весовых коэффициентах Wj, равных 1/()2, где N = 0, 1, 2 ... для последовательных итераций, расчетные формулы выглядят следующим образом:
Тогда для зависимости I (s = bm) значение b равно Т5/Т3.
Для зависимости II (s = a + bm):
(25)
(26)
7.5.6.3 В случае зависимости I алгебраическая подстановка весовых коэффициентов , причем , приводит к упрощенному выражению:
(27)
и нет необходимости в каких бы то ни было итерациях.
7.5.6.4 В случае зависимости II начальные значения представляют собой исходные значения s, полученные в соответствии с 7.4. Они используются для расчета (j = 1, 2, ... q)
и вычисления а1 и b1 по формулам из 7.5.6.2.
Это приводит к
Затем расчеты повторяют для с целью получения
Та же самая методика могла бы быть теперь повторена еще раз для весовых коэффициентов , вытекающих из данных равенств, однако это повлечет за собой лишь незначительные изменения. Стадия от W0j до W1j является эффективной с точки зрения исключения грубых ошибок в весах, и равенство для должно рассматриваться в качестве окончательного результата.
7.5.7 Стандартное отклонение для lgs не зависит от s, и поэтому в данном случае подходящей является невзвешенная регрессия lgs по .
7.5.8 Для зависимости III расчетные формулы выглядят следующим образом:
и значит
(28)
(29)
7.5.9 В 7.5.9.1 - 7.5.9.3 для одной и той же совокупности данных приводятся примеры аппроксимирующих зависимостей I - III, представленных в 7.5.2. Числовые данные взяты из В.3 приложения В и используются здесь лишь для того, чтобы проиллюстрировать числовую процедуру. Они рассмотрены подробнее в приложении В.
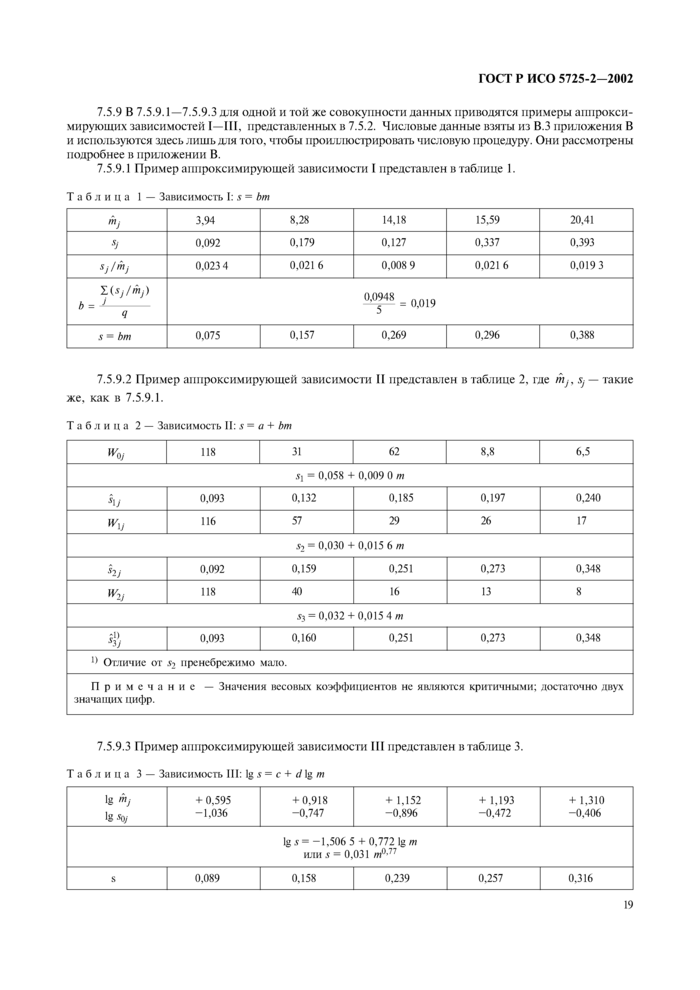
7.5.9.1 Пример аппроксимирующей зависимости I представлен в таблице 1.
Таблица 1 - Зависимость I: s = bm
|
|
3,94 |
8,28 |
14,18 |
15,59 |
20,41 |
|
sj |
0,092 |
0,179 |
0,127 |
0,337 |
0,393 |
|
|
0,023 4 |
0,021 6 |
0,008 9 |
0,021 6 |
0,019 3 |
|
|
|
||||
|
s = bm |
0,075 |
0,157 |
0,269 |
0,296 |
0,388 |
7.5.9.2 Пример аппроксимирующей зависимости II представлен в таблице 2, где , sj - такие же, как в 7.5.9.1.
Таблица 2 - Зависимость II: s = а + bm
|
W0j |
118 |
31 |
62 |
8,8 |
6,5 |
|
s1 = 0,058 + 0,0090 m |
|||||
|
|
0,093 |
0,132 |
0,185 |
0,197 |
0,240 |
|
W1j |
116 |
57 |
29 |
26 |
17 |
|
s2 = 0,030 + 0,0156 m |
|||||
|
|
0,092 |
0,159 |
0,251 |
0,273 |
0,348 |
|
W1j |
118 |
40 |
16 |
13 |
8 |
|
s3 = 0,032 + 0,0154 m |
|||||
|
1) |
0,093 |
0,160 |
0,251 |
0,273 |
0,348 |
|
1) Отличие от s2 пренебрежимо мало. |
|||||
|
Примечание - Значения весовых коэффициентов не являются критичными; достаточно двух значащих цифр. |
|||||
7.5.9.3 Пример аппроксимирующей зависимости III представлен в таблице 3.
Таблица 3 - Зависимость III: lgs = с + dlgm
|
lgs0j |
+0,595 -1,036 |
+0,918 -0,747 |
+1,152 -0,896 |
+1,193 -0,472 |
+1,310 -0,406 |
|
lgs = -1,506 5 + 0,772lgm или s = 0,031m0,77 |
|||||
|
s |
0,089 |
0,158 |
0,239 |
0,257 |
0,316 |
7.6 Статистический анализ как поэтапная процедура
Примечание 5 - На рисунке 3 представлена излагаемая в настоящем подразделе процедура статистического анализа.
7.6.1 Все имеющиеся результаты измерений сводят в одну форму А, представленную на рисунке 2 (см. 7.2). Рекомендуется составить данную форму таким образом, чтобы она имела строк с индексами j = 1, 2, ..., р (представляющих р лабораторий, которые сообщили данные) и q столбцов с индексами j = 1, 2, ..., q (представляющих q уровней в возрастающей последовательности).
В эксперименте с однородными уровнями нет необходимости различать результаты измерений в пределах базового элемента формы А, и они могут заноситься в любом порядке.
7.6.2 Проверяют форму А на предмет каких-либо очевидных нарушений, изучают их и, в случае необходимости, исключают явно ошибочные данные (например, выходящие за пределы диапазона средства измерений или невозможные по техническим соображениям) и докладывают о результатах проверки совету экспертов. Иногда сразу же видно, что результаты измерений в отдельной лаборатории либо в отдельном базовом элементе располагаются на уровне, не совместимом с другими данными. Такого рода явно не согласующиеся результаты должны быть незамедлительно исключены, однако об этом необходимо сообщить совету экспертов с целью дальнейшего рассмотрения (см. 7.7.1).
7.6.3 На основании формы А, скорректированной в необходимых случаях согласно 7.6.2, рассчитывают средние значения для базовых элементов и показатели разброса данных в базовых элементах и заполняют соответственно формы В и С.
Если базовый элемент в форме А содержит только один результат измерений, необходимо принять одно из решений по 7.4.3.
7.6.4 Готовят диаграммы для статистик Манделя h и k, описанные в 7.3.1, и изучают их на предмет совместимости данных. Эти диаграммы могут отображать пригодность данных для дальнейшего анализа, наличие каких-либо возможных выбросовых значений или выпадающих лабораторий. Тем не менее никакие определенные решения на данной стадии не принимают до завершения работ по 7.6.5 - 7.6.9.
7.6.5 Проверяют формы В и С (см. рисунок 2) уровень за уровнем на предмет возможных квазивыбросов и/или статистических выбросов (см. 7.3.2.1а). При этом следует применить статистические критерии, приведенные в 7.3, ко всем сомнительным позициям, отмечая квазивыбросы одной звездочкой, а статистические выбросы - двумя. Если же никаких квазивыбросов или статистических выбросов нет, пропускают этапы 7.6.6 - 7.6.10 и приступают прямо к этапу 7.6.11.
7.6.6 Анализируют вопрос, имеется ли или может ли существовать какое-то техническое объяснение квазивыбросов и/или статистических выбросов и, по возможности, проверяют такое объяснение. В зависимости от результатов корректируют или исключают те квазивыбросы и/или статистические выбросы, которые были удовлетворительно объяснены, и вносят в формы соответствующие исправления. Если после этого никаких квазивыбросов или статистических выбросов не останется, пропускают этапы 7.6.7 - 7.6.10 и приступают прямо к этапу 7.6.11.
Примечание 6 - Большое количество квазивыбросов и/или статистических выбросов может свидетельствовать о резко выраженных расхождениях дисперсий в базовых элементах или резко выраженных различиях между лабораториями, и в связи с этим может возникнуть сомнение в пригодности метода измерений. Об этом необходимо доложить совету экспертов.
7.6.7 Если распределение необъясненных квазивыбросов или статистических выбросов в формах В или С не наводит на мысль о каких-либо выпадающих лабораториях (см. 7.2.5), то пропускают этап 7.6.8 и приступают прямо к этапу 7.6.9.
7.6.8 При наличии убедительных оснований против сомнительных лабораторий, достаточных для исключения некоторых либо всех их данных, исключают соответствующие данные и докладывают об этом совету экспертов.
Решение об исключении некоторых либо всех данных, полученных от отдельной лаборатории, принимает эксперт по статистике, осуществляющий анализ, однако об этом следует сообщить совету экспертов с целью дальнейшего рассмотрения (см. 7.7.1).
7.6.9 Если какие-либо квазивыбросы и/или статистические выбросы остаются необъясненными либо не относятся к выпадающей лаборатории, исключают статистические выбросы, но сохраняют квазивыбросы.
7.6.10 Если на предыдущих стадиях какая-либо запись в форме В была исключена, то тогда должна быть также исключена соответствующая запись в форме С, и наоборот.
7.6.11 Исходя из данных, которые были сохранены в качестве корректных в формах В и С, рассчитывают, пользуясь формулами, приведенными в 7.4, для каждого уровня отдельно среднее значение и стандартные отклонения повторяемости и воспроизводимости.
7.6.12 Если в эксперименте используют только один уровень или если было принято решение о том, что стандартные отклонения повторяемости и воспроизводимости должны быть даны отдельно для каждого уровня (см. 7.5.1) непосредственно в численном виде, а не в виде функциональной зависимости от уровня, то пропускают этапы 7.6.13 - 7.6.18 и приступают прямо к этапу 7.6.19.
Примечание 7 - Последующие этапы 7.6.13 - 7.6.17 применяют по отношению как к sr, так и к sR в отдельности, однако для краткости эти пункты написаны только для sr.
Рисунок 3 - Структурная схема принципиальных этапов статистического анализа
(см. продолжение)
Рисунок 3 (продолжение)
7.6.13 Строят график функции sj по аргументу и на его основе делают вывод, зависит от s от т или нет. Если s признают зависящим от т, пренебрегают этапом 7.6.14 и приступают к этапу 7.6.15. Если s оценивают как не зависящее от т, приступают к этапу 7.6.14. Если возникают сомнения, то лучше всего проработать оба варианта и предоставить возможность принимать решение совету экспертов. Никакого подходящего статистического критерия, обеспечивающего аналитический подход к данной проблеме, не существует, однако технические эксперты, знакомые с методом измерений, должны обладать достаточным опытом для принятия решения.
7.6.14 Используют выражение для окончательной оценки значения стандартного отклонения повторяемости. Пренебрегая этапами 7.6.15 - 7.6.18, приступают непосредственно к этапу 7.6.19.
7.6.15 Исходя из графика, упомянутого в 7.6.13, делают вывод, может ли зависимость между s и т быть выражена прямой линией, и если да, то является ли подходящей зависимость I (s = bm) или II (s = а + bm) (см. 7.5.2). Определяют параметр b или два параметра а и b, пользуясь процедурой, изложенной в 7.5.6. Если линейную зависимость признают удовлетворительной, пропускают этап 7.6.16 и приступают непосредственно к этапу 7.6.17. Если же нет, то приступают к этапу 7.6.16.
7.6.16 Строят график функции lgsj по аргументу и делают, исходя из этого графика, вывод, есть ли основания представить зависимость между lgs и lgm прямой линией или нет. В первом случае определяют параметры с и d зависимости III (lg s = с + dlgm), пользуясь процедурой, приведенной в 7.5.8.
7.6.17 Если на этапе 7.6.15 или 7.6.16 было установлено удовлетворительное соотношение, то окончательными значениями sr (или sR) считают сглаженные значения, полученные из данной зависимости для заданных значений т. Пренебрегая этапом 7.6.18, приступают к этапу 7.6.19.
7.6.18 Если на этапе 7.6.15 или 7.6.16 не было установлено никакого удовлетворительного соотношения, то эксперт по статистике должен решить, может ли быть установлено какое-либо другое соотношение между s и m, или, в качестве альтернативы, настолько ли нерегулярны данные, что установление функциональной зависимости представляется невозможным.
7.6.19 Готовят доклад, демонстрирующий основные данные и результаты, а также выводы из статистического анализа, и представляют его совету экспертов. Для иллюстрации совместимости или изменчивости результатов может оказаться полезным графическое представление по 7.3.1.
7.7 Доклад совету экспертов и принимаемые им решения
7.7.1 Доклад эксперта по статистике
Завершив статистический анализ, эксперт по статистике должен представить на рассмотрение совету экспертов доклад. В докладе должна быть следующая информация:
a) полный перечень наблюдений, полученных от операторов и/или инспекторов, знающих стандарт на метод измерений;
b) полный перечень лабораторий, которые были исключены как выпадающие на этапах 7.6.2 и 7.6.8, и основания для их исключения;
c) полный перечень обнаруженных квазивыбросов и/или статистических выбросов с пояснениями, были ли они объяснены и исправлены или исключены;
d) форма с окончательными результатами для , sr, sR и перечень выводов, сделанных на этапах 7.6.13, 7.6.15 или 7.6.16, проиллюстрированных одним из графиков, рекомендованных для этих этапов;
e) формы А, В и С (рисунок 2), использованные при статистическом анализе, - возможно, в качестве приложения.
7.7.2 Решения, принимаемые советом экспертов
Совет экспертов затем должен обсудить данный доклад и принять решения по следующим вопросам.
a) Являются ли несогласующиеся результаты, квазивыбросы или выбросы, если таковые имеются, следствием недостатков в тексте стандарта на метод измерений?
b) Какие меры должны быть приняты по отношению к исключенным выпадающим лабораториям?
c) Свидетельствуют ли результаты выпадающих и/или комментарии, полученные от операторов и инспекторов, о необходимости совершенствования стандарта на метод измерений? Если да, то какие именно улучшения требуются?
d) Могут ли результаты эксперимента по оценке прецизионности быть основой для установления значений стандартных отклонений повторяемости и воспроизводимости? Если да, то каковы эти значения, в какой форме они должны быть опубликованы и какова сфера применения данных о прецизионности?
7.7.3 Полный доклад
На завершающей стадии ответственным исполнителем должен быть подготовлен для одобрения советом экспертов доклад, детально излагающий основания для работы и как она была организована, включающий в себя доклад эксперта по статистике и подробное изложение согласованных выводов. Часто бывает полезным какое-либо графическое представление совместимости или изменчивости результатов. Доклад должен быть направлен лицам, отвечающим за санкционирование работ, а также другим заинтересованным организациям и компаниям.
8 Статистические таблицы
8.1 Критические значения для критерия Кохрена (см. 7.3.3) представлены в таблице 4.
8.2 Критические значения для критерия Граббса (см. 7.3.4) представлены в таблице 5.
При применении критерия Граббса к одному предельному значению выброс или квазивыброс устанавливают в случае превышения значениями статистики Граббса приведенных в этой таблице 1 %-ных или 5 %-ных критических значений соответственно.
При применении критерия Граббса к двум предельным значениям выброс или квазивыброс устанавливают в случае, если значения статистики Граббса меньше приведенных в этой таблице 1 %-ных или 5 %-ных критических значений соответственно.
Таблица 4 - Критические значения для критерия Кохрена
|
р |
n = 2 |
n = 3 |
n = 4 |
n = 5 |
n = 6 |
|||||
|
1 % |
5 % |
1 % |
5 % |
1 % |
5 % |
1 % |
5 % |
1 % |
5 % |
|
|
2 |
- |
- |
0,995 |
0,975 |
0,979 |
0,939 |
0,959 |
0,906 |
0,937 |
0,877 |
|
3 |
0,993 |
0,967 |
0,942 |
0,871 |
0,883 |
0,798 |
0,834 |
0,746 |
0,793 |
0,707 |
|
4 |
0,968 |
0,906 |
0,864 |
0,768 |
0,781 |
0,684 |
0,721 |
0,629 |
0,676 |
0,590 |
|
5 |
0,928 |
0,841 |
0,788 |
0,684 |
0,696 |
0,598 |
0,633 |
0,544 |
0,588 |
0,506 |
|
6 |
0,883 |
0,781 |
0,722 |
0,616 |
0,626 |
0,532 |
0,564 |
0,480 |
0,520 |
0,445 |
|
7 |
0,838 |
0,727 |
0,664 |
0,561 |
0,568 |
0,480 |
0,508 |
0,431 |
0,466 |
0,397 |
|
8 |
0,794 |
0,680 |
0,615 |
0,516 |
0,521 |
0,438 |
0,463 |
0,391 |
0,423 |
0,360 |
|
9 |
0,754 |
0,638 |
0,573 |
0,478 |
0,481 |
0,403 |
0,425 |
0,358 |
0,387 |
0,329 |
|
10 |
0,718 |
0,602 |
0,536 |
0,445 |
0,447 |
0,373 |
0,393 |
0,331 |
0,357 |
0,303 |
|
11 |
0,684 |
0,570 |
0,504 |
0,417 |
0,418 |
0,348 |
0,366 |
0,308 |
0,332 |
0,281 |
|
12 |
0,653 |
0,541 |
0,475 |
0,392 |
0,392 |
0,326 |
0,343 |
0,288 |
0,310 |
0,262 |
|
13 |
0,624 |
0,515 |
0,450 |
0,371 |
0,369 |
0,307 |
0,322 |
0,271 |
0,291 |
0,243 |
|
14 |
0,599 |
0,492 |
0,427 |
0,352 |
0,349 |
0,291 |
0,304 |
0,255 |
0,274 |
0,232 |
|
15 |
0,575 |
0,471 |
0,407 |
0,335 |
0,332 |
0,276 |
0,288 |
0,242 |
0,259 |
0,220 |
|
16 |
0,553 |
0,452 |
0,388 |
0,319 |
0,316 |
0,262 |
0,274 |
0,230 |
0,246 |
0,208 |
|
17 |
0,532 |
0,434 |
0,372 |
0,305 |
0,301 |
0,250 |
0,261 |
0,219 |
0,234 |
0,198 |
|
18 |
0,514 |
0,418 |
0,356 |
0,293 |
0,288 |
0,240 |
0,249 |
0,209 |
0,223 |
0,189 |
|
19 |
0,496 |
0,403 |
0,343 |
0,281 |
0,276 |
0,230 |
0,238 |
0,200 |
0,214 |
0,181 |
|
20 |
0,480 |
0,389 |
0,330 |
0,270 |
0,265 |
0,220 |
0,229 |
0,192 |
0,205 |
0,174 |
|
21 |
0,465 |
0,377 |
0,318 |
0,261 |
0,255 |
0,212 |
0,220 |
0,185 |
0,197 |
0,167 |
|
22 |
0,450 |
0,365 |
0,307 |
0,252 |
0,246 |
0,204 |
0,212 |
0,178 |
0,189 |
0,160 |
|
23 |
0,437 |
0,354 |
0,297 |
0,243 |
0,238 |
0,197 |
0,204 |
0,172 |
0,182 |
0,155 |
|
24 |
0,425 |
0,343 |
0,287 |
0,235 |
0,230 |
0,191 |
0,197 |
0,166 |
0,176 |
0,149 |
|
25 |
0,413 |
0,334 |
0,278 |
0,228 |
0,222 |
0,185 |
0,190 |
0,160 |
0,170 |
0,144 |
|
26 |
0,402 |
0,325 |
0,270 |
0,221 |
0,215 |
0,179 |
0,184 |
0,155 |
0,164 |
0,140 |
|
27 |
0,391 |
0,316 |
0,262 |
0,215 |
0,209 |
0,173 |
0,179 |
0,150 |
0,159 |
0,135 |
|
28 |
0,382 |
0,308 |
0,255 |
0,209 |
0,202 |
0,168 |
0,173 |
0,146 |
0,154 |
0,131 |
|
29 |
0,372 |
0,300 |
0,248 |
0,203 |
0,196 |
0,164 |
0,168 |
0,142 |
0,150 |
0,127 |
|
30 |
0,363 |
0,293 |
0,241 |
0,198 |
0,191 |
0,159 |
0,164 |
0,138 |
0,145 |
0,124 |
|
31 |
0,355 |
0,286 |
0,235 |
0,193 |
0,186 |
0,155 |
0,159 |
0,134 |
0,141 |
0,120 |
|
32 |
0,347 |
0,280 |
0,229 |
0,188 |
0,181 |
0,151 |
0,155 |
0,131 |
0,138 |
0,117 |
|
33 |
0,339 |
0,273 |
0,224 |
0,184 |
0,177 |
0,147 |
0,151 |
0,127 |
0,134 |
0,114 |
|
34 |
0,332 |
0,267 |
0,218 |
0,179 |
0,172 |
0,144 |
0,147 |
0,124 |
0,131 |
0,111 |
|
35 |
0,325 |
0,262 |
0,213 |
0,175 |
0,168 |
0,140 |
0,144 |
0,121 |
0,127 |
0,108 |
|
36 |
0,318 |
0,256 |
0,208 |
0,172 |
0,165 |
0,137 |
0,140 |
0,118 |
0,124 |
0,106 |
|
37 |
0,312 |
0,251 |
0,204 |
0,168 |
0,161 |
0,134 |
0,137 |
0,116 |
0,121 |
0,103 |
|
38 |
0,306 |
0,246 |
0,200 |
0,164 |
0,157 |
0,131 |
0,134 |
0,113 |
0,119 |
0,101 |
|
39 |
0,300 |
0,242 |
0,196 |
0,161 |
0,154 |
0,129 |
0,131 |
0,111 |
0,116 |
0,099 |
|
40 |
0,294 |
0,237 |
0,192 |
0,158 |
0,151 |
0,126 |
0,128 |
0,108 |
0,114 |
0,097 |
|
р - количество лабораторий для данного уровня; n - количество результатов измерений в базовом элементе (см. 7.3.3.3). |
||||||||||
Таблица 5 - Критические значения для критерия Граббса
|
р |
Одно наибольшее или одно наименьшее |
Два наибольших или два наименьших |
||
|
Свыше 1 % |
Свыше 5 % |
Ниже 1 % |
Ниже 5 % |
|
|
3 |
1,155 |
1,155 |
- |
- |
|
4 |
1,496 |
1,481 |
0,0000 |
0,0002 |
|
5 |
1,764 |
1,715 |
0,0018 |
0,0090 |
|
6 |
1,973 |
1,887 |
0,0116 |
0,0349 |
|
7 |
2,139 |
2,020 |
0,0308 |
0,0708 |
|
8 |
2,274 |
2,126 |
0,0563 |
0,1101 |
|
9 |
2,387 |
2,215 |
0,0851 |
0,1492 |
|
10 |
2,482 |
2,290 |
0,1150 |
0,1864 |
|
11 |
2,564 |
2,355 |
0,1448 |
0,2213 |
|
12 |
2,636 |
2,412 |
0,1738 |
0,2537 |
|
13 |
2,699 |
2,462 |
0,2016 |
0,2836 |
|
14 |
2,755 |
2,507 |
0,2280 |
0,3112 |
|
15 |
2,806 |
2,549 |
0,2530 |
0,3367 |
|
16 |
2,852 |
2,585 |
0,2767 |
0,3603 |
|
17 |
2,894 |
2,620 |
0,2990 |
0,3822 |
|
18 |
2,932 |
2,651 |
0,3200 |
0,4025 |
|
19 |
2,968 |
2,681 |
0,3398 |
0,4214 |
|
20 |
3,001 |
2,709 |
0,3585 |
0,4391 |
|
21 |
3,031 |
2,733 |
0,3761 |
0,4556 |
|
22 |
3,060 |
2,758 |
0,3927 |
0,4711 |
|
23 |
3,087 |
2,781 |
0,4085 |
0,4857 |
|
24 |
3,112 |
2,802 |
0,4234 |
0,4994 |
|
25 |
3,135 |
2,822 |
0,4376 |
0,5123 |
|
26 |
3,157 |
2,841 |
0,4510 |
0,5245 |
|
27 |
3,178 |
2,859 |
0,4638 |
0,5360 |
|
28 |
3,199 |
2,876 |
0,4759 |
0,5470 |
|
29 |
3,218 |
2,893 |
0,4875 |
0,5574 |
|
30 |
3,236 |
2,908 |
0,4985 |
0,5672 |
|
31 |
3,253 |
2,924 |
0,5091 |
0,5766 |
|
32 |
3,270 |
2,938 |
0,5192 |
0,5856 |
|
33 |
3,286 |
2,952 |
0,5288 |
0,5941 |
|
34 |
3,301 |
2,965 |
0,5381 |
0,6023 |
|
35 |
3,316 |
2,979 |
0,5469 |
0,6101 |
|
36 |
3,330 |
2,991 |
0,5554 |
0,6175 |
|
37 |
3,343 |
3,003 |
0,5636 |
0,6247 |
|
38 |
3,356 |
3,014 |
0,5714 |
0,6316 |
|
39 |
3,369 |
3,025 |
0,5789 |
0,6382 |
|
40 |
3,381 |
3,036 |
0,5862 |
0,6445 |
|
р - количество лабораторий для данного уровня; Примечание - Таблица воспроизведена с разрешения Американской статистической ассоциации [3]. |
||||
8.3 Индикаторы для статистик Манделя h и k (см. 7.3.1) представлены в таблицах 6 и 7.
Таблица 6 - Индикаторы для статистик Манделя h и k на 1 %-ном уровне значимости
|
р |
h |
k |
||||||||
|
п |
||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
3 |
1,15 |
1,71 |
1,64 |
1,58 |
1,53 |
1,49 |
1,46 |
1,43 |
1,41 |
1,39 |
|
4 |
1,49 |
1,91 |
1,77 |
1,67 |
1,60 |
1,55 |
1,51 |
1,48 |
1,45 |
1,43 |
|
5 |
1,72 |
2,05 |
1,85 |
1,73 |
1,65 |
1,59 |
1,55 |
1,51 |
1,48 |
1,46 |
|
6 |
1,87 |
2,14 |
1,90 |
1,77 |
1,68 |
1,62 |
1,57 |
1,53 |
1,50 |
1,47 |
|
7 |
1,98 |
2,20 |
1,94 |
1,79 |
1,70 |
1,63 |
1,58 |
1,54 |
1,51 |
1,48 |
|
8 |
2,06 |
2,25 |
1,97 |
1,81 |
1,71 |
1,65 |
1,59 |
1,55 |
1,52 |
1,49 |
|
9 |
2,13 |
2,29 |
1,99 |
1,82 |
1,73 |
1,66 |
1,60 |
1,56 |
1,53 |
1,50 |
|
10 |
2,18 |
2,32 |
2,00 |
1,84 |
1,74 |
1,66 |
1,61 |
1,57 |
1,53 |
1,50 |
|
11 |
2,22 |
2,34 |
2,01 |
1,85 |
1,74 |
1,67 |
1,62 |
1,57 |
1,54 |
1,51 |
|
12 |
2,25 |
2,36 |
2,02 |
1,85 |
1,75 |
1,68 |
1,62 |
1,58 |
1,54 |
1,51 |
|
13 |
2,27 |
2,38 |
2,03 |
1,86 |
1,76 |
1,68 |
1,63 |
1,58 |
1,55 |
1,52 |
|
14 |
2,30 |
2,39 |
2,04 |
1,87 |
1,76 |
1,69 |
1,63 |
1,58 |
1,55 |
1,52 |
|
15 |
2,32 |
2,41 |
2,05 |
1,87 |
1,76 |
1,69 |
1,63 |
1,59 |
1,55 |
1,52 |
|
16 |
2,33 |
2,42 |
2,05 |
1,88 |
1,77 |
1,69 |
1,63 |
1,59 |
1,55 |
1,52 |
|
17 |
2,35 |
2,44 |
2,06 |
1,88 |
1,77 |
1,69 |
1,64 |
1,59 |
1,55 |
1,52 |
|
18 |
2,36 |
2,44 |
2,06 |
1,88 |
1,77 |
1,70 |
1,64 |
1,59 |
1,56 |
1,52 |
|
19 |
2,37 |
2,44 |
2,07 |
1,89 |
1,78 |
1,70 |
1,64 |
1,59 |
1,56 |
1,53 |
|
20 |
2,39 |
2,45 |
2,07 |
1,89 |
1,78 |
1,70 |
1,64 |
1,60 |
1,56 |
1,53 |
|
21 |
2,39 |
2,46 |
2,07 |
1,89 |
1,78 |
1,70 |
1,64 |
1,60 |
1,56 |
1,53 |
|
22 |
2,40 |
2,46 |
2,08 |
1,90 |
1,78 |
1,70 |
1,65 |
1,60 |
1,56 |
1,53 |
|
23 |
2,41 |
2,47 |
2,08 |
1,90 |
1,78 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
24 |
2,42 |
2,47 |
2,08 |
1,90 |
1,79 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
25 |
2,42 |
2,47 |
2,08 |
1,90 |
1,79 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
26 |
2,43 |
2,48 |
2,09 |
1,90 |
1,79 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
27 |
2,44 |
2,48 |
2,09 |
1,90 |
1,79 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
28 |
2,44 |
2,49 |
2,09 |
1,91 |
1,79 |
1,71 |
1,65 |
1,60 |
1,57 |
1,53 |
|
29 |
2,45 |
2,49 |
2,09 |
1,91 |
1,79 |
1,71 |
1,65 |
1,60 |
1,57 |
1,53 |
|
30 |
2,45 |
2,49 |
2,10 |
1,91 |
1,79 |
1,71 |
1,65 |
1,61 |
1,57 |
1,53 |
|
p - количество лабораторий для данного уровня; n - количество параллельных определений в пределах каждой лаборатории для данного уровня. Примечание - Материал предоставлен доктором Дж. Манделем |
||||||||||
Таблица 7 - Индикаторы для статистик Манделя h и k на 5 %-ном уровне значимости
|
р |
h |
k |
|||||||||
|
п |
|||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||
|
3 |
1,15 |
1,65 |
1,53 |
1,45 |
1,40 |
1,37 |
1,34 |
1,32 |
1,30 |
1,29 |
|
|
4 |
1,42 |
1,76 |
1,59 |
1,50 |
1,44 |
1,40 |
1,37 |
1,35 |
1,33 |
1,31 |
|
|
5 |
1,57 |
1,81 |
1,62 |
1,53 |
1,46 |
1,42 |
1,39 |
1,36 |
1,34 |
1,32 |
|
|
6 |
1,66 |
1,85 |
1,64 |
1,54 |
1,48 |
1,43 |
1,40 |
1,37 |
1,35 |
1,33 |
|
|
7 |
1,71 |
1,87 |
1,66 |
1,55 |
1,49 |
1,44 |
1,41 |
1,38 |
1,36 |
1,34 |
|
|
8 |
1,75 |
1,88 |
1,67 |
1,56 |
1,50 |
1,45 |
1,41 |
1,38 |
1,36 |
1,34 |
|
|
9 |
1,78 |
1,90 |
1,68 |
1,57 |
1,50 |
1,45 |
1,42 |
1,39 |
1,36 |
1,35 |
|
|
10 |
1,80 |
1,90 |
1,68 |
1,57 |
1,50 |
1,46 |
1,42 |
1,39 |
1,37 |
1,35 |
|
|
11 |
1,82 |
1,91 |
1,69 |
1,58 |
1,51 |
1,46 |
1,42 |
1,39 |
1,37 |
1,35 |
|
|
12 |
1,83 |
1,92 |
1,69 |
1,58 |
1,51 |
1,46 |
1,42 |
1,40 |
1,37 |
1,35 |
|
|
13 |
1,84 |
1,92 |
1,69 |
1,58 |
1,51 |
1,46 |
1,43 |
1,40 |
1,37 |
1,35 |
|
|
14 |
1,85 |
1,92 |
1,70 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,37 |
1,35 |
|
|
15 |
1,86 |
1,93 |
1,70 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
|
16 |
1,86 |
1,93 |
1,70 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
|
17 |
1,87 |
1,93 |
1,70 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
|
18 |
1,88 |
1,93 |
1,71 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
|
19 |
1,88 |
1,93 |
1,71 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
|
20 |
1,89 |
1,94 |
1,71 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
|
21 |
1,89 |
1,94 |
1,71 |
1,60 |
1,52 |
1,47 |
1,44 |
1,41 |
1,38 |
1,36 |
|
|
22 |
1,89 |
1,94 |
1,71 |
1,60 |
1,52 |
1,47 |
1,44 |
1,41 |
1,38 |
1,36 |
|
|
23 |
1,90 |
1,94 |
1,71 |
1,60 |
1,53 |
1,47 |
1,44 |
1,41 |
1,38 |
1,36 |
|
|
24 |
1,90 |
1,94 |
1,71 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,38 |
|
|
25 |
1,90 |
1,94 |
1,71 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
|
26 |
1,90 |
1,94 |
1,71 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
|
27 |
1,91 |
1,94 |
1,71 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
|
28 |
1,91 |
1,94 |
1,71 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
|
29 |
1,91 |
1,94 |
1,72 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
|
30 |
1,91 |
1,94 |
1,72 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
|
p - количество лабораторий для данного уровня; n - количество параллельных определений в пределах каждой лаборатории для данного уровня. Примечание - Материал предоставлен доктором Дж. Манделем. |
|||||||||||
ПРИЛОЖЕНИЕ А
(обязательное)
Условные обозначения и сокращения, используемые в ГОСТ Р ИСО 5725
|
а |
Отсекаемый на оси ординат отрезок в соотношении s = а + bт |
|
А |
Показатель, используемый для расчета неопределенности оценки |
|
b |
Угловой коэффициент прямой в соотношении s = а + bт |
|
В |
Лабораторная составляющая систематической погрешности измерений при реализации конкретного метода - разность между систематической погрешностью лаборатории при реализации конкретного метода измерений (конкретной МВИ) и систематической погрешностью метода измерений |
|
B0 |
Составляющая величины В, представляющая все факторы, которые не изменяются в условиях промежуточной прецизионности |
|
В(1), B(2) и т.д. |
Составляющие величины В, представляющие факторы, которые изменяются в условиях промежуточной прецизионности |
|
с |
Отсекаемый на оси ординат отрезок в соотношении lgs = с + dlgm |
|
С, С¢, С" |
Тестовые статистики |
|
Сcrit, С¢crit, C²crit |
Критические значения для статистик |
|
CDp |
Критическая разность для вероятности Р |
|
CRp |
Критический диапазон для вероятности Р |
|
d |
Угловой коэффициент прямой в соотношении lgs = с + dlgm |
|
е |
Составляющая результата измерений, представляющая случайную погрешность каждого результата измерений |
|
f |
Коэффициент критического диапазона |
|
Fp(v1, v2) |
p-квантиль F-распределения с v1 и v2 степенями свободы |
|
G |
Статистика Граббса |
|
h |
Статистика Манделя для межлабораторной совместимости |
|
k |
Статистика Манделя для внутрилабораторной совместимости |
|
LCL |
Нижний предел контроля (действия либо предупреждения) |
|
т |
Общее среднее значение измеряемой характеристики; уровень |
|
М |
Количество факторов, рассматриваемых в условиях промежуточной прецизионности |
|
N |
Количество повторений (итераций) |
|
n |
Количество результатов измерений, полученных в одной лаборатории на одном уровне (т.е. в пределах ячейки - базового элемента) |
|
р |
Количество лабораторий, участвующих в межлабораторном эксперименте |
|
Р |
Вероятность |
|
q |
Количество уровней измеряемой характеристики в межлабораторном эксперименте |
|
r |
Предел повторяемости (сходимости) |
|
R |
Предел воспроизводимости |
|
RM |
Стандартный образец |
|
s |
Оценка стандартного отклонения |
|
|
Прогнозируемое стандартное отклонение |
|
Т |
Итог или сумма какого-либо выражения |
|
t |
Количество объектов испытаний или групп объектов |
|
UCL |
Верхний предел контроля (действия либо предупреждения) |
|
W |
Весовой коэффициент, используемый при расчете взвешенной регрессии |
|
w |
Диапазон изменения выборки результатов измерений |
|
х |
Заданная величина, используемая для критерия Граббса |
|
у |
Результат измерений (испытаний) |
|
|
Среднее арифметическое значение результатов измерений (испытаний) |
|
|
Общее среднее значение результатов измерений (испытаний) |
|
a |
Уровень значимости |
|
b |
Вероятность ошибки второго рода |
|
g |
Отношение стандартного отклонения воспроизводимости к стандартному отклонению повторяемости (сходимости) (sR/sr) |
|
D |
Систематическая погрешность лаборатории при реализации конкретного стандартного метода измерений (конкретной МВИ) |
|
|
Оценка D |
|
d |
Систематическая погрешность метода измерений |
|
|
Оценка d |
|
l |
Поддающаяся обнаружению разность между систематическими погрешностями двух лабораторий при реализации одного и того же метода измерений или систематическими погрешностями двух методов измерений (МВИ) одного и того же назначения на идентичных образцах |
|
m |
Истинное или принятое опорное значение измеряемой величины (характеристики) |
|
v |
Число степеней свободы |
|
r |
Поддающееся обнаружению соотношение между стандартными отклонениями повторяемости (сходимости) для методов В и А |
|
s |
Истинное (действительное) значение стандартного отклонения |
|
t |
Составляющая результата измерений, представляющая изменение, обусловленное временем, прошедшим с момента последней калибровки |
|
j |
Поддающееся обнаружению соотношение между квадратными корнями из межлабораторных средних квадратов для методов В и А |
|
|
p-квантиль c2-распределения с v степенями свободы |
Символы, используемые в качестве подстрочных индексов
|
С |
Различие, определяемое калибровкой |
|
Е |
Различие, определяемое оборудованием |
|
i |
Идентификатор для конкретной лаборатории |
|
I() |
Идентификатор для промежуточных мер прецизионности; в скобках - идентификация типа промежуточной ситуации |
|
j |
Идентификатор для уровня (ГОСТ Р ИСО 5725-2) |
|
Идентификатор для группы испытаний или для фактора (ГОСТ Р ИСО 5725-3) |
|
|
k |
Идентификатор для конкретного результата испытаний в лаборатории i на уровне j |
|
L |
Межлабораторный |
|
m |
Идентификатор для поддающейся обнаружению систематической погрешности |
|
М |
Различие, обусловленное неидентичностью проб (образцов) |
|
О |
Различие, определяемое сменой оператора |
|
Р |
Вероятность |
|
r |
Повторяемость |
|
R |
Воспроизводимость |
|
Т |
Различие, обусловленное периодом (временем), в течение которого проводят измерения или оценочный эксперимент |
|
W |
Внутрилабораторный |
|
1, 2, 3 ... |
Для результатов измерений, нумеруемых в порядке их получения |
|
(1), (2), (3) ... |
Для результатов измерений (испытаний), нумеруемых в порядке возрастания измеряемой величины |
ПРИЛОЖЕНИЕ В
(справочное)
Примеры статистического анализа экспериментов по оценке прецизионности
В.1 Пример 1. Определение содержания серы в угле (несколько уровней без недостающих данных и без выбросов)
B.1.1 Общие положения
a) Метод измерений
Определение содержания серы в угле (результаты измерений выражают в процентах по массе).
b) Источник
Tomkins, S.S: Industrial and Engineering Chemistry (Analytical edition), 14, 1942, pp 141 - 145 [4].
c) Описание
В эксперименте принимали участие восемь лабораторий, которые провели анализ в соответствии со стандартным методом измерений, описанным в приведенном выше источнике [4]. Лаборатория № 1 сообщила о четырех результатах анализа, а лаборатория № 5 - о четырех или пяти; остальные лаборатории выполнили по три измерения.
d) Графическое представление
Обычно для графического представления данных используют статистики Манделя h и k, однако из-за того, что в данном примере они недостаточно иллюстрированы, статистики были заменены диаграммами других типов. Диаграммы Манделя полностью проиллюстрированы и рассмотрены в примере В.3.
B.1.2 Исходные данные
Исходные данные представлены в процентах по массе [% (m/m)] в таблице В.1, выполненной по форме А рисунка 2 (см. 7.2.8), и не вызывают особых замечаний.
Графические представления этих данных даны на рисунках В.1 - В.4.
Таблица В.1 - Исходные данные. Содержание серы в угле, в процентах по массе
|
Номер лаборатории i |
Уровень j |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
0,71 |
1,20 |
1,68 |
3,26 |
|
0,71 |
1,18 |
1,70 |
3,26 |
|
|
0,70 |
1,23 |
1,68 |
3,20 |
|
|
0,71 |
1,21 |
1,69 |
3,24 |
|
|
2 |
0,69 |
1,22 |
1,64 |
3,20 |
|
0,67 |
1,21 |
1,64 |
3,20 |
|
|
0,68 |
1,22 |
1,65 |
3,20 |
|
|
3 |
0,66 |
1,28 |
1,61 |
3,37 |
|
0,65 |
1,31 |
1,61 |
3,36 |
|
|
0,69 |
1,30 |
1,62 |
3,38 |
|
|
4 |
0,67 |
1,23 |
1,68 |
3,16 |
|
0,65 |
1,18 |
1,66 |
3,22 |
|
|
0,66 |
1,20 |
1,66 |
3,23 |
|
|
5 |
0,70 |
1,31 |
1,64 |
3,20 |
|
0,69 |
1,22 |
1,67 |
3,19 |
|
|
0,66 |
1,22 |
1,60 |
3,18 |
|
|
0,71 |
1,24 |
1,66 |
3,27 |
|
|
0,69 |
- |
1,68 |
3,24 |
|
|
6 |
0,73 |
1,39 |
1,70 |
3,27 |
|
0,74 |
1,36 |
1,73 |
3,31 |
|
|
0,73 |
1,37 |
1,73 |
3,29 |
|
|
7 |
0,71 |
1,20 |
1,69 |
3,27 |
|
0,71 |
1,26 |
1,70 |
3,24 |
|
|
0,69 |
1,26 |
1,68 |
3,23 |
|
|
8 |
0,70 |
1,24 |
1,67 |
3,25 |
|
0,65 |
1,22 |
1,68 |
3,25 |
|
|
0,68 |
1,30 |
1,67 |
3,26 |
|
Примечание 8 - В эксперименте, результаты которого представлены в таблице В.1, лаборатории не инструктировались относительно необходимого числа измерений; указывалось только минимальное число (равное трем для каждого базового элемента). Согласно рекомендованной процедуре, изложенной в настоящем стандарте, для лабораторий № 1 и № 5, представивших большее число результатов, должен быть произведен случайный отбор трех из них. Однако чтобы проиллюстрировать процедуру расчета для разного количества результатов измерений в базовых элементах, в этом примере все результаты были сохранены. Читатель сам может произвести случайный отбор с целью уменьшения количества результатов измерений до трех в каждом базовом элементе и убедиться, что в данном случае такое изменение процедуры оказывает относительно малое влияние на значения , sr и sR.
В.1.3 Расчет средних значений для базовых элементов ()
Средние значения для базовых элементов представлены в процентах по массе [% (m/m)] в таблице В.2, выполненной по форме В рисунка 2 (см. 7.2.9).
В.1.4 Расчет стандартных отклонений (sij)
Стандартные отклонения представлены в процентах по массе [% (m/m)] в таблице В.3, выполненной по форме В рисунка 2 (см. 7.2.10).
В.1.5 Проверка на совместимость и наличие выбросов
При n = 3 и числе лабораторий p = 8 критические значения для критерия Кохрена равны 0,516 для 5 % и 0,615 для 1 %.
Для уровня 1 наибольшее значение s имеет место в лаборатории № 8; при этом Ss2 = 0,00182; тестовая статистика = 0,347.
Для уровня 2 наибольшее значение s имеет место в лаборатории № 5; при этом Ss2 = 0,00636; тестовая статистика = 0,287.
Для уровня 3 наибольшее значение s имеет место в лаборатории № 5; при этом Ss2 = 0,00172; тестовая статистика = 0,598.
Для уровня 4 наибольшее значение s имеет место в лаборатории № 4; при этом Ss2 = 0,00463; тестовая статистика = 0,310.
Таблица В.2 - Средние значения в базовых элементах. Содержание серы в угле, в процентах по массе
|
Номер лаборатории i |
Уровень j |
|||||||
|
1 |
2 |
3 |
4 |
|||||
|
|
nij |
|
nij |
|
nij |
|
nij |
|
|
1 |
0,708 |
4 |
1,205 |
4 |
1,688 |
4 |
3,240 |
4 |
|
2 |
0,680 |
3 |
1,217 |
3 |
1,643 |
3 |
3,200 |
3 |
|
3 |
0,667 |
3 |
1,297 |
3 |
1,613 |
3 |
3,370 |
3 |
|
4 |
0,660 |
3 |
1,203 |
3 |
1,667 |
3 |
3,203 |
3 |
|
5 |
0,690 |
5 |
1,248 |
4 |
1,650 |
5 |
3,216 |
5 |
|
6 |
0,733 |
3 |
1,373 |
3 |
1,720 |
3 |
3,290 |
3 |
|
7 |
0,703 |
3 |
1,240 |
3 |
1,690 |
3 |
3,247 |
3 |
|
8 |
0,677 |
3 |
1,253 |
3 |
1,673 |
3 |
3,257 |
3 |
Таблица В.3 - Стандартные отклонения. Содержание серы в угле, в процентах по массе
|
Номер лаборатории i |
Уровень j |
|||||||
|
1 |
2 |
3 |
4 |
|||||
|
sij |
nij |
sij |
nij |
sij |
nij |
sij |
nij |
|
|
1 |
0,005 |
4 |
0,021 |
4 |
0,010 |
4 |
0,028 |
4 |
|
2 |
0,010 |
3 |
0,006 |
3 |
0,006 |
3 |
0,000 |
3 |
|
3 |
0,021 |
3 |
0,015 |
3 |
0,006 |
3 |
0,010 |
3 |
|
4 |
0,010 |
3 |
0,025 |
3 |
0,012 |
3 |
0,038 |
3 |
|
5 |
0,019 |
5 |
0,043 |
4 |
0,032 |
5 |
0,038 |
5 |
|
6 |
0,006 |
3 |
0,015 |
3 |
0,017 |
3 |
0,020 |
3 |
|
7 |
0,012 |
3 |
0,035 |
3 |
0,010 |
3 |
0,021 |
3 |
|
8 |
0,025 |
3 |
0,042 |
3 |
0,006 |
3 |
0,006 |
3 |
Полученные результаты означают, что один базовый элемент на уровне 3 можно считать квазивыбросом и что выбросов нет. Квазивыброс сохраняют в последующих расчетах.
Применение критерия Граббса к средним значениям базовых элементов дало результаты, представленные в таблице В.4. В данном случае нет единичных квазивыбросов или выбросов. На уровнях 2 и 4 высокие результаты для лабораторий № 3 и № 6 согласно тестовой статистике для двух пиков представляют собой квазивыбросы; они были сохранены в анализе.
Рисунок В.1 - Содержание серы в угле, уровень (образец) 1
Рисунок В.2 - Содержание серы в угле, уровень (образец) 2
Рисунок В.3 - Содержание серы в угле, уровень (образец) 3
Рисунок В.4 - Содержание серы в угле, уровень (образец) 4
В.1.6 Расчет , srj и sRj
Дисперсии, аналитическое представление которых дано в 7.4.4 и 7.4.5, рассчитывают нижеследующим образом, с использованием уровня 1 в качестве примера.
Количество лабораторий р = 8
sr = 0,01524.
sR = 0,02632.
Расчеты для уровней 2, 3 и 4 могут быть выполнены аналогичным образом, что приведет к результатам, представленным в таблице В.5.
В.1.7 Зависимость прецизионности от m
Рассмотрение данных, содержащихся в таблице В.5, не обнаруживает какой-либо зависимости, и поэтому в качестве показателей прецизионности могут быть использованы средние значения стандартных отклонений srj и SRj.
В.1.8 Выводы
Меры прецизионности для данного метода измерений, выраженные в процентах по массе, имеют следующие значения:
- стандартное отклонение повторяемости sr = 0,022;
- стандартное отклонение воспроизводимости SR = 0,045.
Таблица В.4 - Применение критерия Граббса к средним значениям в базовых элементах
|
Уровень |
Одиночный нижний |
Одиночный верхний |
Двойной нижний |
Двойной верхний |
Значения |
|
1 |
1,24 |
1,80 |
0,539 |
0,298 |
Значения статистики Граббса |
|
2 |
0,91 |
2,09 |
0,699 |
0,108 |
|
|
3 |
1,67 |
1,58 |
0,378 |
0,459 |
|
|
4 |
0,94 |
2,09 |
0,679 |
0,132 |
|
|
Квазивыбросы |
2,126 |
2,126 |
0,110 1 |
0,110 1 |
Критические значения Граббса |
|
Выбросы |
2,274 |
2,274 |
0,056 3 |
0,056 3 |
Таблица В.5 - Расчетные значения , srj и sRj для содержания серы в угле, в процентах по массе
|
Уровень j |
pj |
|
srj |
sRj |
|
1 |
8 |
0,690 |
0,015 |
0,026 |
|
2 |
8 |
1,252 |
0,029 |
0,061 |
|
3 |
8 |
1,667 |
0,017 |
0,035 |
|
4 |
8 |
3,250 |
0,025 |
0,058 |
Данные значения стандартных отклонений повторяемости и воспроизводимости могут быть применены в диапазоне содержания серы 0,69 - 3,25 % по массе. Они были определены на основании эксперимента с однородными уровнями, в котором участвовало восемь лабораторий, представивших результаты в этом диапазоне, в которых были обнаружены и сохранены четыре квазивыброса.
В.2 Пример 2. Точка размягчения смолы (несколько уровней с недостающими данными)
B.2.1 Общие положения
a) Метод измерений
Определение точки размягчения смолы при помощи кольца и шарика.
b) Источник
Стандартные методы испытаний дегтя и аналогичных продуктов.
Раздел «Смолы». Метод серии РТЗ с использованием нейтрального глицерина [5].
c) Материал
Материал был отобран из промышленных партий смолы, собран и подготовлен согласно указаниям, приведенным в части «Пробы» раздела «Смолы» [5].
d) Описание
При определении точки размягчения смолы измерения температуры производились в градусах Цельсия. В эксперименте участвовало 16 лабораторий. С целью охватить стандартный набор технических смол, предполагалось произвести измерения на четырех образцах (уровнях), имеющих точки размягчения вблизи 87,5, 92,5, 97,5 и 102,5 °С. Однако для уровня 2 был выбран не соответствующий требованиям материал со средней температурой размягчения около 96 °С, который скорее соответствовал уровню 3. Лаборатория № 5 вначале неправильно провела анализ пробы для уровня 2 (эта проба измерялась первой), в результате чего у нее осталось недостаточно материала для выполнения еще одного измерения на этом уровне. Лаборатория № 8 обнаружила, что у нее вообще нет образца для уровня 1 (она располагала двумя образцами для уровня 4).
e) Графические изображения
Статистики Манделя h и k должны были быть представлены на диаграмме, но снова в этом примере они не использовались и были заменены другим типом графического представления данных. Диаграммы Манделя полностью проиллюстрированы и рассмотрены в примере, приведенном в В.3.
B.2.2 Исходные данные
Исходные данные представлены в градусах Цельсия в таблице В.6, выполненной по форме А рисунка 2 (см. 7.2.8).
В.2.3 Средние значения для базовых элементов
Средние значения для базовых элементов представлены в градусах Цельсия в таблице В.7, выполненной по форме В рисунка 2 (см. 7.2.9).
Графическое изображение этих данных представлено на рисунке В.5.
Таблица В.6 - Исходные данные. Точка размягчения смолы, °С
|
Номер лаборатории i |
Уровень j |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
91,0 |
97,0 |
96,5 |
104,0 |
|
89,6 |
97,2 |
97,0 |
104,0 |
|
|
2 |
89,7 |
98,5 |
97,2 |
102,6 |
|
89,8 |
97,2 |
97,0 |
103,6 |
|
|
3 |
88,0 |
97,8 |
94,2 |
103,0 |
|
87,5 |
94,5 |
95,8 |
99,5 |
|
|
4 |
89,2 |
96,8 |
96,0 |
102,5 |
|
88,5 |
97,5 |
98,0 |
103,5 |
|
|
5 |
89,0 |
97,2 |
98,2 |
101,0 |
|
90,0 |
- |
98,5 |
100,2 |
|
|
6 |
88,5 |
97,8 |
99,5 |
102,2 |
|
90,5 |
97,2 |
103,2 |
102,0 |
|
|
7 |
88,9 |
96,6 |
98,2 |
102,8 |
|
88,2 |
97,5 |
99,0 |
102,2 |
|
|
8 |
- |
96,0 |
98,4 |
102,6 |
|
- |
97,5 |
97,4 |
103,9 |
|
|
9 |
90,1 |
95,5 |
98,2 |
102,8 |
|
88,4 |
96,8 |
96,7 |
102,0 |
|
|
10 |
86,0 |
95,2 |
94,8 |
99,8 |
|
85,8 |
95,0 |
93,0 |
100,8 |
|
|
11 |
87,6 |
93,2 |
93,6 |
98,2 |
|
84,4 |
93,4 |
93,9 |
97,8 |
|
|
12 |
88,2 |
95,8 |
95,8 |
101,7 |
|
87,4 |
95,4 |
95,4 |
101,2 |
|
|
13 |
91,0 |
98,2 |
98,0 |
104,5 |
|
90,4 |
99,5 |
97,0 |
105,6 |
|
|
14 |
87,5 |
97,0 |
97,1 |
105,2 |
|
87,8 |
95,5 |
96,6 |
101,8 |
|
|
15 |
87,5 |
95,0 |
97,8 |
101,5 |
|
87,6 |
95,2 |
99,2 |
100,9 |
|
|
16 |
88,8 |
95,0 |
97,2 |
99,5 |
|
85,0 |
93,2 |
97,8 |
99,8 |
|
|
Примечание - Очевидных квазивыбросов или статистических выбросов нет. |
||||
В.2.4 Абсолютные расхождения в базовых элементах
В данном примере в каждом базовом элементе имеются два результата измерений, и для характеристики их различий могут быть использованы абсолютные расхождения, представленные в таблице В.8, выполненной по форме В рисунка 2 (см. 7.2.10).
Графическое изображение этих данных представлено на рисунке В.6.
Таблица В.7 - Средние значения для базовых элементов. Точка размягчения смолы, °С
|
Номер лаборатории i |
Уровень j |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
90,30 |
97,10 |
96,75 |
104,00 |
|
2 |
89,75 |
97,85 |
97,10 |
103,10 |
|
3 |
87,75 |
96,15 |
95,00 |
101,25 |
|
4 |
88,85 |
97,15 |
97,00 |
103,00 |
|
5 |
89,50 |
- |
98,35 |
100,60 |
|
6 |
89,50 |
97,50 |
101,35 |
102,10 |
|
7 |
88,55 |
97,05 |
98,60 |
102,50 |
|
8 |
- |
96,75 |
97,90 |
103,25 |
|
9 |
89,25 |
96,15 |
97,45 |
102,40 |
|
10 |
85,90 |
95,10 |
93,90 |
100,30 |
|
11 |
86,00 |
93,30 |
93,75 |
98,00 |
|
12 |
87,80 |
95,60 |
95,60 |
101,45 |
|
13 |
90,70 |
98,85 |
97,50 |
105,05 |
|
14 |
87,65 |
96,25 |
96,85 |
103,50 |
|
15 |
87,55 |
95,10 |
98,50 |
101,20 |
|
16 |
86,90 |
94,10 |
97,50 |
99,65 |
|
Примечание - Результат для i = 5, j = 2 был исключен (см. 7.4.3). |
||||
Таблица В.8 - Абсолютные расхождения в базовых элементах. Точка размягчения смолы, °С
|
Номер лаборатории i |
Уровень j |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
1,4 |
0,2 |
0,5 |
0,0 |
|
2 |
0,1 |
1,3 |
0,2 |
1,0 |
|
3 |
0,5 |
3,3 |
1,6 |
3,5 |
|
4 |
0,7 |
0,7 |
2,0 |
1,0 |
|
5 |
1,0 |
- |
0,3 |
0,8 |
|
6 |
2,0 |
0,6 |
3,7 |
0,2 |
|
7 |
0,7 |
0,9 |
0,8 |
0,6 |
|
8 |
- |
1,5 |
1,0 |
1,3 |
|
9 |
1,7 |
1,3 |
1,5 |
0,8 |
|
10 |
0,2 |
0,2 |
1,8 |
1,0 |
|
11 |
3,2 |
0,2 |
0,3 |
0,4 |
|
12 |
0,8 |
0,4 |
0,4 |
0,5 |
|
13 |
0,6 |
1,3 |
1,0 |
1,1 |
|
14 |
0,3 |
1,5 |
0,5 |
3,4 |
|
15 |
0,1 |
0,2 |
1,4 |
0,6 |
|
16 |
3,8 |
1,8 |
0,6 |
0,3 |
B.2.5 Проверка на совместимость и наличие выбросов
Применение критерия Кохрена дает значения статистики С, представленные в таблице В.9. Критические значения (см. 8.1) на уровне 5 %-ной значимости при n = 2 составляют 0,471 для р = 15 и 0,452 для р = 16. Никаких квазивыбросов не отмечено.
При применении к средним значениям в базовых элементах критериев Граббса не было обнаружено ни единичных, ни двойных квазивыбросов или выбросов (см. таблицу В.10).
B.2.6 Расчет , srj и sRj
Эти величины рассчитаны в соответствии с 7.4.4 и 7.4.5.
Для уровня 1, используемого в качестве примера, и n = 2 расчеты выглядят следующим образом (с целью облегчения арифметических действий из всех данных вычтено 80,00).
Количество лабораторий р = 15.
Количество параллельных определений n = 2.
sr = 1,1092.
sR = 1,6697.
Значения для всех четырех уровней (образцов) представлены в таблице В.11.
Таблица В.9 - Значения статистики Кохрена С
|
Уровень j |
1 |
2 |
3 |
4 |
|
С |
0,391 (15) |
0,424 (15) |
0,434 (16) |
0,380(16) |
|
Примечание - В скобках приведено количество лабораторий. |
||||
Таблица В.10 - Применение критерия Граббса для анализа средних значений в базовых элементах
|
Уровень и |
Одиночный нижний |
Одиночный верхний |
Двойной нижний |
Двойной верхний |
Значения |
|
1; 15 |
1,69 |
1,56 |
0,546 |
0,662 |
Значения статистики Граббса |
|
2; 15 |
2,04 |
1,77 |
0,478 |
0,646 |
|
|
3; 16 |
1,76 |
2,27 |
0,548 |
0,566 |
|
|
4; 16 |
2,22 |
1,74 |
0,500 |
0,672 |
|
|
Квазивыбросы |
Критические значения Граббса |
||||
|
п = 15 |
2,549 |
2,549 |
0,3367 |
0,3367 |
|
|
п = 16 |
2,585 |
2,585 |
0,3603 |
0,3603 |
|
|
Выбросы |
|||||
|
п = 15 |
2,806 |
2,806 |
0,2530 |
0,2530 |
|
|
n = 16 |
2,852 |
2,652 |
0,2767 |
0,2767 |
Таблица В.11 - Расчетные значения , srj и sRj для точки размягчения смолы
|
Уровень j |
pi |
, °С |
srj |
sRj |
|
1 |
15 |
88,40 |
1,109 |
1,670 |
|
2 |
15 |
96,27 |
0,925 |
1,597 |
|
3 |
16 |
97,07 |
0,993 |
2,010 |
|
4 |
16 |
101,96 |
1,004 |
1,915 |
Рисунок В.5 - Точка размягчения смолы. Средние значения в базовых элементах
Рисунок В.6 - Точка размягчения смолы. Абсолютные расхождения в базовых элементах
B.2.7 Зависимость прецизионности от т
При рассмотрении таблицы В.11 не обнаружено какой-либо явной зависимости. Изменения по диапазону значений т, если таковые вообще имеются, слишком малы, чтобы их считать существенными. Более того, ввиду малого диапазона значений т и характера измерений, наличие зависимости от т едва ли можно ожидать. Представляется оправданным вывод, что прецизионность в данном диапазоне, который был выбран как охватывающий материал стандартного типа, не зависит от т; поэтому в качестве окончательных значений для стандартных отклонений повторяемости и воспроизводимости могут приниматься средние значения по уровням.
В.2.8 Выводы
Для практического применения данного метода измерений значения прецизионности могут считаться не зависящими от уровня материала (от значения измеряемой величины) и составляют:
- стандартное отклонение повторяемости sr = 1,0 °С
- стандартное отклонение воспроизводимости sR = 1,8 °С.
В.3 Пример 3 - Термометрическое титрование креозотового масла (несколько уровней с выбросами)
B.3.1 Общие положения
a) Источник
Стандартные методы испытаний гудрона и аналогичных продуктов. Раздел «Креозотовое масло» [5].
b) Материал
Материал был отобран от промышленных партий креозотового масла, собран и подготовлен в соответствии с указаниями части «Пробы» раздела «Креозотовое масло» [5].
c) Описание
Экспериментальному изучению подвергся стандартный метод количественного химического анализа, предусматривающий термометрическое титрование с выражением результатов измерений в процентах по массе. В измерениях принимали участие девять лабораторий, использовавших по пять образцов в двух экземплярах (дубликатах) каждый. Образцы отбирались таким образом, чтобы охватить стандартный диапазон, характерный для общепромышленного применения, а именно - чтобы образцы приближенно соответствовали уровням 4, 8, 12, 16 и 20 (в процентах по массе). Общепринятая практика предусматривает регистрацию результатов измерений только до одного десятичного знака, однако в данном эксперименте операторам было дано указание регистрировать результаты измерений до двух десятичных знаков.
B.3.2 Исходные данные
Исходные данные представлены в процентах по массе в таблице В.12, выполненной по форме А рисунка 2 (см. 7.2.8).
Результаты измерений лаборатории № 1 были всегда выше, а на некоторых уровнях существенно выше по сравнению с результатами измерений других лабораторий.
Второй результат измерений лаборатории № 6 на уровне 5 сомнителен; зарегистрированное значение гораздо лучше подошло бы к уровню 4.
Эти вопросы подробнее рассматривают в В.3.5.
B.3.3 Средние значения для базовых элементов
Средние значения для базовых элементов представлены в процентах по массе в таблице В.13, выполненной по форме В рисунка 2 (см. 7.2.9).
B.3.4 Абсолютные расхождения в базовых элементах
Абсолютные расхождения wij, представлены в процентах по массе в таблице В.14, выполненной по форме С рисунка 2 (см. 7.2.10).
Таблица В.12 - Исходные данные. Термометрическое титрование креозотового масла, в процентах по массе
|
Номер лаборатории i |
Уровень j |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
4,44 4,39 |
9,34 9,34 |
17,40 16,90 |
19,23 19,23 |
24,28 24,00 |
|
2 |
4,03 4,23 |
8,42 8,33 |
14,42 14,50 |
16,06 16,22 |
20,40 19,91 |
|
3 |
3,70 3,70 |
7,60 7,40 |
13,60 13,60 |
14,50 15,10 |
19,30 19,70 |
|
4 |
4,10 4,10 |
8,93 8,80 |
14,60 14,20 |
15,60 15,50 |
20,30 20,30 |
|
5 |
3,97 4,04 |
7,89 8,12 |
13,73 13,92 |
15,54 15,78 |
20,53 20,88 |
|
6 |
3,75 4,03 |
8,76 9,24 |
13,90 14,06 |
16,42 16,58 |
18,56 16,58 |
|
7 |
3,70 3,80 |
8,00 8,30 |
14,10 14,20 |
14,90 16,00 |
19,70 20,50 |
|
8 |
3,91 3,90 |
8,04 8,07 |
14,84 14,84 |
15,41 15,22 |
21,10 20,78 |
|
9 |
4,02 4,07 |
8,44 8,17 |
14,24 14,10 |
15,14 15,44 |
20,71 21,66 |
Таблица В.13 - Средние значения для базовых элементов. Термометрическое титрование креозотового масла, в процентах по массе
|
Номер лаборатории i |
Уровень j |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
4,415 |
9,340 |
17,150** |
19,230** |
24,140* |
|
2 |
4,130 |
8,375 |
14,460 |
16,140 |
20,155 |
|
3 |
3,700 |
7,500 |
13,600 |
14,800 |
19,500 |
|
4 |
4,100 |
8,865 |
14,400 |
15,550 |
20,300 |
|
5 |
4,005 |
8,005 |
13,825 |
15,660 |
20,705 |
|
6 |
3,890 |
9,000 |
13,980 |
16,500 |
17,570 |
|
7 |
3,750 |
8,150 |
14,150 |
15,450 |
20,100 |
|
8 |
3,905 |
8,055 |
14,840 |
15,315 |
20,940 |
|
9 |
4,045 |
8,305 |
14,170 |
15,290 |
21,185 |
|
* Рассматривают как квазивыброс. ** Рассматривают как статистический выброс. |
|||||
В.3.5 Проверка на совместимость и наличие выбросов
Расчет статистик совместимости Манделя h и k (см. 7.3.1) дал значения, представленные на рисунках В.7 и В.8. Горизонтальные линии на диаграммах соответствуют значениям индикаторов Манделя, взятым из 8.3.
Диаграмма для h (рисунок В.7) недвусмысленно указывает на то, что лаборатория № 1 получала гораздо большие значения по сравнению со всеми остальными лабораториями на всех уровнях. Такие результаты требуют внимания совета экспертов, руководящих этим межлабораторным экспериментом. Если для этих результатов измерений невозможно найти никаких объяснений, то специалисты должны вынести свое заключение, основанное на дополнительных или, может быть, нестатических рассуждениях, и на этой основе решить, включать или не включать данные этой лаборатории в расчеты значений прецизионности.
Диаграмма для k (рисунок В.8) демонстрирует, в первую очередь, значительные расхождения между параллельными определениями в лабораториях № 6 и № 7. Тем не менее эти результаты не представляются настолько существенными, чтобы требовать принятия каких-то особых мер, помимо поиска возможных объяснений, и, в случае необходимости, - корректирующих действий в лабораториях.
Применение критерия Кохрена приводит к следующим результатам (см. таблицу В.14).
На уровне 4 абсолютное расхождение 1,10 (лаборатория № 7) приводит к значению статистики Кохрена, составляющему 1,102/1,8149 = 0,667.
На уровне 5 абсолютное расхождение 1,98 (лаборатория № 6) приводит к значению статистики Кохрена, составляющему 1,982/6,1663 = 0,636.
Для девяти лабораторий критические значения для критерия Кохрена составляют 0,638 для 5 % и 0,754 для 1 %.
Значение 1,10 на уровне 4 явно представляет собой квазивыброс, а значение 1,98 на уровне 5 настолько близко к 5 %-ному уровню, что также может быть возможным квазивыбросом. Поскольку два этих значения существенно отличаются от всех остальных и их присутствие значительно увеличивает делитель в статистике Кохрена, они оба были отнесены к квазивыбросам и помечены звездочкой. Для их исключения нет достаточных оснований, несмотря на то, что диаграмма Манделя k (рисунок В.8) также дает повод усомниться в этих значениях.
Применение критериев Граббса к средним значениям в базовых элементах дает результаты, представленные в таблице В.15.
Поскольку использование критерия Граббса для одного предельного значения указывают на выбросы на уровнях 3 и 4, для двух предельных значений критерий Граббса на этих уровнях не применялся (см. 7.3.4).
Средние значения в базовых элементах на уровнях 3 и 4 для данных лаборатории № 1 определены как выбросы. Среднее значение в базовом элементе этой лаборатории на уровне 5 также высоко. Это явно видно и из диаграммы Манделя для h (рисунок В.7).
При дальнейшем исследовании оказалось, что по крайней мере одна из проб для уровня 5 в лаборатории № 6 могла быть ошибочно отнесена к уровню 5 с уровня 4. Поскольку абсолютное расхождение для данного базового элемента также было сомнительным, было принято решение, что данную пару результатов измерений тоже можно исключить. Без данной пары значений результат измерений для лаборатории № 1 на уровне 5 тем более является сомнительным.
Таблица В.14 - Абсолютные расхождения в базовых элементах. Термометрическое титрование креозотового масла
|
Номер лаборатории i |
Уровень j |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
0,05 |
0,00 |
0,50 |
0,00 |
0,28 |
|
2 |
0,20 |
0,09 |
0,08 |
0,16 |
0,49 |
|
3 |
0,00 |
0,20 |
0,00 |
0,60 |
0,40 |
|
4 |
0,00 |
0,13 |
0,40 |
0,10 |
0,00 |
|
5 |
0,07 |
0,23 |
0,19 |
0,24 |
0,35 |
|
6 |
0,28 |
0,48 |
0,16 |
0,16 |
1,98* |
|
7 |
0,10 |
0,30 |
0,10 |
1,10* |
0,80 |
|
8 |
0,01 |
0,03 |
0,00 |
0,19 |
0,32 |
|
9 |
0,05 |
0,27 |
0,14 |
0,30 |
0,95 |
|
* Рассматривают как квазивыброс. |
|||||
По изложенным причинам было решено исключить пару результатов измерений лаборатории № 6 для уровня 5, так как было неясно, какая проба материала анализировалась, и исключить все результаты измерений от лаборатории № 1 как исходящие от выпадающей лаборатории. Без учета исключенных результатов измерений статистика Кохрена на уровне 4 была составлена с критическим значением для восьми лабораторий (0,680 при 5 %), в результате чего соответствующие данные для уровня 4 уже не приводили к квазивыбросу и были сохранены.
Таблица В.15 - Применение критерия Граббса к средним значениям в базовых элементах
|
Уровень |
Одиночный нижний |
Одиночный верхний |
Двойной нижний |
Двойной верхний |
Значения |
|
1 |
1,36 |
1,95 |
0,502 |
0,356 |
Значения статистики Граббса |
|
2 |
1,57 |
1,64 |
0,540 |
0,395 |
|
|
3 |
0,86 |
2,50 |
- |
- |
|
|
4 |
0,91 |
2,47 |
- |
- |
|
|
5 |
1,70 |
2,10 |
0,501 |
0,318 |
|
|
Квазивыбросы |
2,215 |
2,215 |
0,1492 |
0,1492 |
Критические значения Граббса |
|
Выбросы |
2,387 |
2,387 |
0,0851 |
0,0851 |
Рисунок В.7 - Титрование креозотового масла. Значения статистики межлабораторной совместимости Манделя h, сгруппированные по лабораториям
Рисунок В.8 - Титрование креозотового масла. Значения статистики внутрилабораторной совместимости Манделя k, сгруппированные по лабораториям
В.3.6 Расчет , srj и sRj.
Значения , srj и sRj рассчитанные без учета данных лаборатории № 1 и пары результатов измерений лаборатории № 6 на уровне 5, представлены в таблице В.16, выраженные в процентах по массе; при этом расчет производился в соответствии с 7.4.4 и 7.4.5.
В.3.7 Зависимость прецизионности от т
Из таблицы В.16 видно, что стандартные отклонения возрастают с повышением значений т, следовательно вполне вероятно, что может быть установлена некая форма функциональной зависимости.
Собственно расчеты по аппроксимации функциональной зависимости здесь не представлены, поскольку они уже были детально изложены для sr в 7.5.9. Значения srj и sRj приведены в виде графика функции, построенного по аргументу на рисунке В.9.
Из рисунка В.9 очевидно, что аппроксимирующие значения для уровня 3 в значительной степени отклоняются от значений, найденных из данных эксперимента, и что аппроксимация не может быть улучшена ни одной из альтернативных процедур (см. 7.5.2).
Для адекватной повторяемости представляется прямая линия, проходящая через начало координат.
Для воспроизводимости все три линии демонстрируют адекватное согласование с данными; наилучшее согласование обеспечивает зависимость III.
Любой специалист, знакомый с требованиями, предъявляемыми к стандартному методу измерений для креозотового масла, сможет выбрать наиболее подходящую зависимость.
В.3.8 Окончательные значения прецизионности
Окончательные значения прецизионности, округленные должным образом, следующие:
- стандартное отклонение повторяемости sr = 0,019m;
- стандартное отклонение воспроизводимости sR = 0,086 + 0,030m или sR = 0,078m0,72.
В.3.9 Выводы
Нет никаких статистических оснований для того, чтобы отдать предпочтение какому-то одному из двух выражений для sR в В.3.8. Решение, какое из них использовать, должно быть принято советом экспертов.
Необходимо найти причину выбросов результатов измерений лаборатории № 1.
Скорее всего описанный эксперимент по оценке прецизионности был неудовлетворительным. Одна из девяти лабораторий была признана выпадающей, а другая - провела измерения на неправильном образце. Проба материала для уровня 3 по-видимому была неверно отобрана, так как результаты ее анализа почти те же, что и результаты для уровня (пробы) 4, вместо того, чтобы располагаться посредине между уровнями 2 и 4. Более того, проба материала для уровня 3 в некоторой степени отличалась от других проб по структуре, будучи более однородной. Было бы полезно повторить данный эксперимент, уделив больше внимания отбору материалов для различных уровней (проб с различными значениями измеряемых характеристик).
Таблица В.16 - Расчетные значения , srj и sRj для термометрического титрования креозотового масла
|
Уровень j |
pi |
|
srj |
sRj |
|
1 |
8 |
3,94 |
0,092 |
0,171 |
|
2 |
8 |
8,28 |
0,179 |
0,498 |
|
3 |
8 |
14,18 |
0,127 |
0,400 |
|
4 |
8 |
15,59 |
0,337 |
0,579 |
|
5 |
7 |
20,41 |
0,393 |
0,637 |
Рисунок В.9 - График функций srj и sRj по аргументу , представляющий функциональные зависимости, получаемые в соответствии с 7.5 на основании данных таблицы В.16
ПРИЛОЖЕНИЕ С
(справочное)
Библиография
[1] ISO 3534-1:1993 Statistics-Vocabulary and symbols - Part 1: Statistical methods. Terms and definitions
[2] ASTM E691-87, Standard Practice for Conducting ab Interlaboratory Study to Determine the Precision of a Test Method. American Society for Testing and Materials, Philadelphia, PA, USA
[3] GRUBBS, F.E. and BECK, G. Extension of sample sizes and percentage points for significance tests of outlying observations. Technometrics, 14, 1972, pp. 847 - 854
[4] TOMKINS, S.S. Industrial and Engineering Chemistry (Analytical edition), 14, 1942, pp. 141 - 145
[5] «Standard Methods for Testing Tar and its Products». 7th Ed. Standardisation of Tar Products Tests Committee, 1979
[6] ISO 3534-2:1993 Statistics-Vocabulary and symbols - Part 2: Statistical quality control
[7] ISO 3534-3:1985 Statistics-Vocabulary and symbols - Part 3: Design of experiments
Ключевые слова: измерение, испытания, метод измерений, стандартизация метода измерений, результаты измерений, результаты испытаний, точность, правильность, прецизионность, систематическая погрешность, повторяемость, воспроизводимость, случайная погрешность, эксперимент по оценке точности, альтернативный метод измерений, статистический анализ