ГОСТ Р ИСО 22514-6-2014
Статистические методы. Управление процессами. Часть 6. Статистики воспроизводимости процесса для многомерного нормального распределения
Устанавливает методы вычисления статистик воспроизводимости и пригодности процессов для многомерных количественных характеристик, в тех случаях, когда необходимо (или выгодно) рассматривать набор одномерных характеристик. Методы, приведенные в стандарте, разработаны на основе двумерного нормального распределения.
Идентичен ISO 22514-6:2013
Переиздание. Октябрь 2016 г.
Оглавление
1 Область применения
2 Нормативные ссылки
3 Термины и определения
4 Сокращения и обозначения
5 Анализ процесса
6 Использование многомерных индексов воспроизводимости и пригодности процесса
7 Вычисление индексов воспроизводимости и пригодности процесса
8 Примеры
Приложение А (справочное) Обоснование использованных формул
Приложение В (справочное) Пример оценки воспроизводимости для дисбаланса оси
Приложение С (справочное) Пример оценки воспроизводимости для позиционного отклонения оси отверстия
Приложение D (справочное) Построение функции качества
Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов ссылочным национальным стандартам Российской Федерации
Библиография
40 страниц
| Дата введения | 01.12.2015 |
|---|---|
| Добавлен в базу | 12.02.2016 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Строительство
- Раздел Экология
Организации:
| 29.10.2014 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 1455-ст |
|---|---|---|---|
| Разработан | АО НИЦ КД | ||
| Издан | Стандартинформ | 2015 г. | |
| Издан | Стандартинформ | 2016 г. |
Statistical methods. Process management. Part 6. Process capability statistics for multivariate normal distribution
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9
стр. 10
стр. 11
стр. 12

стр. 13

стр. 14

стр. 15
стр. 16
стр. 17
стр. 18
стр. 19
стр. 20
стр. 21
стр. 22

стр. 23

стр. 24

стр. 25

стр. 26

стр. 27

стр. 28
стр. 29
стр. 30
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
НАЦИОНАЛЬНЫЙ
СТАНДАРТ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ГОСТРИСО 22514-6— 2014
Статистические методы УПРАВЛЕНИЕ ПРОЦЕССАМИ
Ч а с т ь 6
Статистики воспроизводимости процесса для многомерного нормального распределения
(ISO 22514-6:2013, Statistical methods in process management — Capability and performance — Part 6: Process capability statistics for characteristics following a multivariate normal distribution, IDT)
Издание официальное
Москва
Стандартинформ
2016
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (АО «НИЦ КД») на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Применение статистических методов»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 октября 2014 г. № 1455-ст.
4 Настоящий стандарт идентичен международному стандарту ИСО 22514-6:2013 «Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 6. Статистики воспроизводимости процесса для многомерного нормального распределения» (ISO 22514-6:2013 «Statistical methods in process management - Capability and performance - Part 6: Process capability statistics for characteristics following a multivariate normal distribution»).
Наименование настоящего стандарта изменено относительно наименования указанного международного документа для приведения в соответствие с ГОСТ Р 1.5 — 2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Октябрь 2016 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок - в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
© Стандартинформ, 2016
В Российской Федерации настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
7.2.3 Меньший индекс воспроизводимости процесса
|
Y | |
|
2 3 1 | |
|
ю 5 D S 10 X | |
L
*-
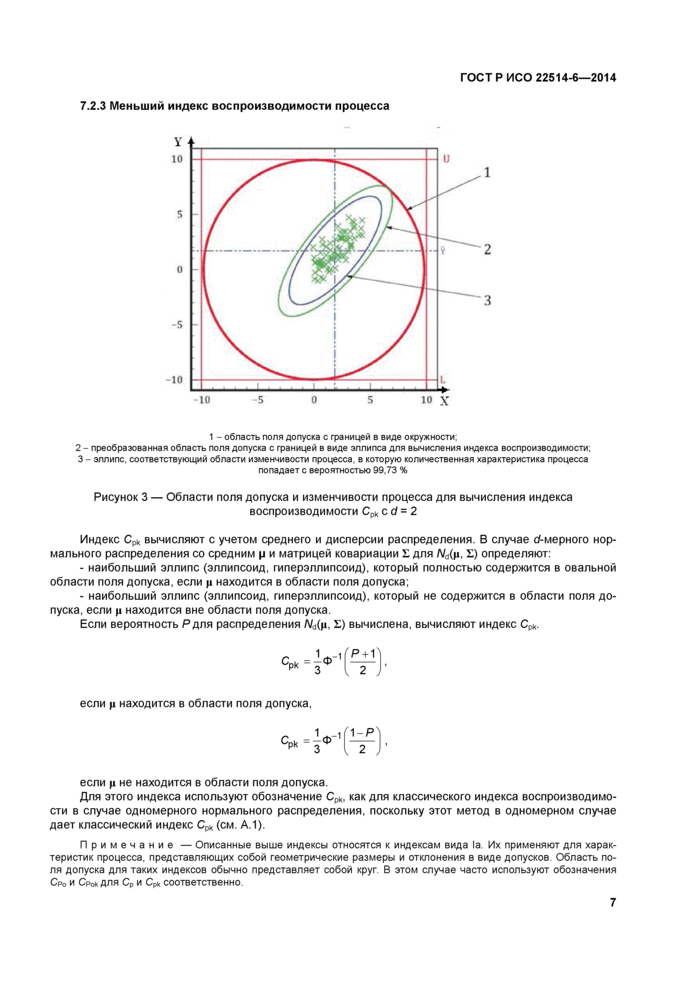
1 - область поля допуска с границей в виде окружности;
2 - преобразованная область поля допуска с границей в виде эллипса для вычисления индекса воспроизводимости;
3 - эллипс, соответствующий области изменчивости процесса, в которую количественная характеристика процесса
попадает с вероятностью 99,73 %
Рисунок 3 — Области поля допуска и изменчивости процесса для вычисления индекса
воспроизводимости Срк с d = 2
Индекс Срк вычисляют с учетом среднего и дисперсии распределения. В случае d-мерного нормального распределения со средним р и матрицей ковариации £ для /Vd(p, £) определяют:
- наибольший эллипс (эллипсоид, гиперэллипсоид), который полностью содержится в овальной области поля допуска, если р находится в области поля допуска;
- наибольший эллипс (эллипсоид, гиперэллипсоид), который не содержится в области поля допуска, если р находится вне области поля допуска.
Если вероятность Рдля распределения /Vd(р, £) вычислена, вычисляют индекс Срк.
если р находится в области поля допуска,
если р не находится в области поля допуска.
Для этого индекса используют обозначение Срк, как для классического индекса воспроизводимости в случае одномерного нормального распределения, поскольку этот метод в одномерном случае дает классический индекс Cpk (см. А.1).
Примечание — Описанные выше индексы относятся к индексам вида 1а. Их применяют для характеристик процесса, представляющих собой геометрические размеры и отклонения в виде допусков. Область поля допуска для таких индексов обычно представляет собой круг. В этом случае часто используют обозначения Ср0 и Срок для Ср и Срк соответственно.
7
7.3 Индексы воспроизводимости видов 1с и Мс
Вычисление индексов воспроизводимости видов 1с и Мс основано на преобразовании многомерной характеристики в одномерную. Для этих индексов многомерный аспект выражен в определении функции преобразования q(x), где х - многомерная величина. Это преобразование должно отражать функциональную значимость одномерных количественных характеристик в х и их взаимосвязь. Например, она описывает модель для области поля допуска и может быть интерпретирована как весовая функция, например, функция потерь или количественная функция, характеризующая техническую функциональность.
|
Рисунок 4 - Этапы вычисления индексов процесса вида 1с и Мс |
Вычисление индексов вида 1с и Мс выполняют последовательно в четыре этапа (см. рисунок 4).
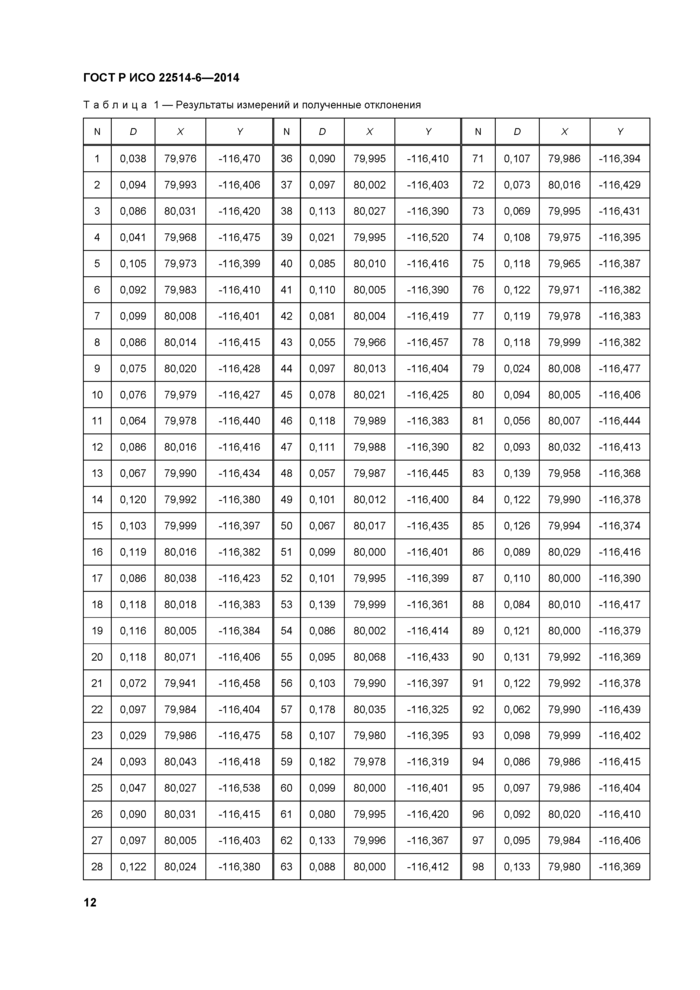
На первом этапе определяют функцию q(x) для d-мерной области поля допуска. Эта функция обладает максимумом со значением qmax в целевой точке области поля допуска. На границе области поля допуска q(x) принимает значение Abound- В некоторых случаях qmax и Abound могут быть получены на основе технической информации обо всех одномерных характеристиках, составляющих х. В других случаях соответствующие значения принимают равными qmax = 1 и Abound = 0,5. Функция q(x) может быть представлена в виде уравнения или кусочно-гладкой функции. Пример функции, составленной из линейных отрезков, представлен на рисунке 5.
|
X - отклонение оси детали; Y - размер ширины паза; 1 - Abound — значение на границе области поля допуска; 2 - рпах = 1, целевое значение; 3 - q(x) контурные линии Рисунок 5 - Пример функции преобразования области поля допуска (ширина/положение) для ММС |
Размеры в миллиметрах
8
ГОСТ Р ИСО 22514-6-2014
На рисунке 5 многомерная характеристика состоит из двух параметров: ширины паза и отклонения его оси. Область допуска имеет сложную форму, составленную из прямоугольника и треугольника. Дальнейшие объяснения примера приведены в разделе 8. Значение c/max = 1 функция принимает при номинальных значениях параметров. От этого значения функция уменьшается к границам поля допуска. Функция может быть любой: линейной, показательной и другой. На рисунке 5 функция q(x) составлена из отрезков линейных функций. Возможны и другие более сложные формы функции с/(х).
На втором этапе отбирают выборку и выполняют измерения характеристик. Результаты измерений формируют в многомерную величину х и преобразуют с помощью функции с/(х) в другие функционально связанные величины.
На третьем этапе, на основе этих значений, должна быть определена соответствующая одномерная функция распределения F(q). Может быть также выполнено второе преобразование к нормальному одномерному случаю. Если функция q(x) монотонно возрастает от границы до целевого значения и случайный вектор X имеет многомерное нормальное распределение, то плотность распределения F(q) является унимодальной.
На четвертом этапе на основе установленного распределения, преобразованного целевого значения и границ поля допуска вычисляют Ср. Если выбраны qrmax = 1 и (/b0Und = 0,5, то 0,5 соответствует нижней допустимой границе, а 1 — верхней естественной границе. Так как q предлагает только односторонний допуск и распределение, ограниченное с одной стороны, для оценки процесса можно использовать только Срк.
Индекс вида I, Срк вычисляют аналогично 7.2.3. Вероятность Р вычисляют на основе одномерного распределения F(q), Р= 1 - F(c/bound).
Индекс вида II может быть вычислен методами, приведенными в ИСО 22514-2. На основе определения CpkL, выбирают Xmid в качестве медианы распределения F(q), L = (/b0Und и AL = Xmid —Xoi135% , тогда Cpk имеет вид:
Срк -
^50% ~ Abound Я50% ~ 9о,135 %
где с/х % - процентиль распределения F(q) уровня х %.
Поскольку Срк содержит информацию об изменчивости и положении процесса относительно границы поля допуска qrbound, необходим индекс только для информации об изменчивости процесса. Этот индекс Ср может быть вычислен с применением методов ИСО 22514-2. Но так как целевое значение (/является максимальным значением, Ср может быть менее Срк.
Если на первом этапе вместо функции /(х) определяют функцию потерь /(х), то она имеет значение /min в целевой точке и /b0Und на границе области поля допуска. Например (хотя, строго говоря, оно не является функцией потерь) отклонение оси буровой скважины D от целевого положения можно интерпретировать как функцию /(х). Эта функция достигает минимума /min = 0 в целевой точке и значения /bound на половине позиционного допуска оси скважины. Область поля допуска представляет собой круг.
7.4 Индексы воспроизводимости процесса видов На и Mb7.4.1 Общие положения
Многомерные индексы воспроизводимости процесса вида II основаны на отношении объема области поля допуска к объему области изменчивости процесса. Если Ц0| - объем области поля допуска и Цжзс - объем области изменчивости процесса, то индекс имеет вид:
Чо1
Цэгос
Показатель степени а позволяет переходить от площади или объема к одномерным измерениям.
Таким образом, обычно а = 11d. В противном случае а = 1.
9
Чтобы сделать объемы областей сопоставимыми, необходимо преобразовать форму областей. Индексы вида Ма преобразовывают исходную область поля допуска в модифицированную, имеющую форму области изменчивости процесса (например, эллипс или гиперэллипс в случае многомерного нормального распределения). Для индексов типа Mb преобразование выполняют для области изменчивости процесса. В этом случае форму области изменчивости процесса адаптируют к форме области поля допуска. Сопоставление ситуаций На и Mb приведено в [9].
Так как этот индекс позволяет получить только информацию об изменчивости процесса относительно поля допуска, желательно дополнительно определять индекс, позволяющий получить информацию о положении вектора среднего р относительно целевого значения.
7.4.2 Вид Ма
Трансформированная область поля допуска определена как наибольший эллипс (или гиперэллипсоид) с целевым значением в центре, полностью содержащийся в исходной области поля допуска (см. рисунок 2 или рисунок 3). В случае области поля допуска, параметры которой xti, xt2... xtd обозначают половину расстояния от границы поля допуска до целевого значения, объем l/t0| имеет вид:
d/2 d
Объем эллипсоида изменчивости процесса для вычисления Ср рассчитывают с учетом того, что многомерная количественная характеристика попадает в этот эллипсоид с вероятностью 99,73:
' ргос
(гс-Хээ.гз)^2
Г(1+|)
где |S| - определитель S (приложение А). Этот индекс соответствует значению I/O и позволяет получить информацию о положении процесса относительно целевого значения ро. Оценка D имеет вид:
Оценку индекса Срт определяют по формуле:
А _ Wo/ 1
Рт ~ V П ' vproc и
Примеры расчета индекса приведены в [7].
7.4.3 Вид Mb
Вид индекса Mb определен в [8]. Форму области изменчивости процесса (эллипс), трансформируют в форму области поля допуска. В случае прямоугольной области поля допуска, это - наименьший прямоугольник (гиперкубоид), в который вписывается данный эллипс (гиперэллипсоид) Определяют значение Ср на основе проекции размеров эллипса (гиперэллипсоида) в каждом направлении L и U.
Примеры расчета индекса приведены в [8].
10
ГОСТ Р ИСО 22514-6-20148 Примеры
8.1 Двумерный позиционный допуск8.1.1 Вид индекса 1а
Рисунок 6 — Схема положения отверстия на детали
~яг
1-Л
\£>
|
Рисунок 6 — Схема положения отверстия на детали |
~яг
1-Л
\£>
На готовой детали выполняют измерения параметров отверстия. Расстояние от края детали до середины отверстия по оси X составляет 80 мм, а по оси У это расстояние составляет 116,5 мм (см. рисунок 6). Диаметр отверстия равен 50 мм с допуском ± 0,05 мм. Информация о геометрических допусках приведена в ИСО 1101.
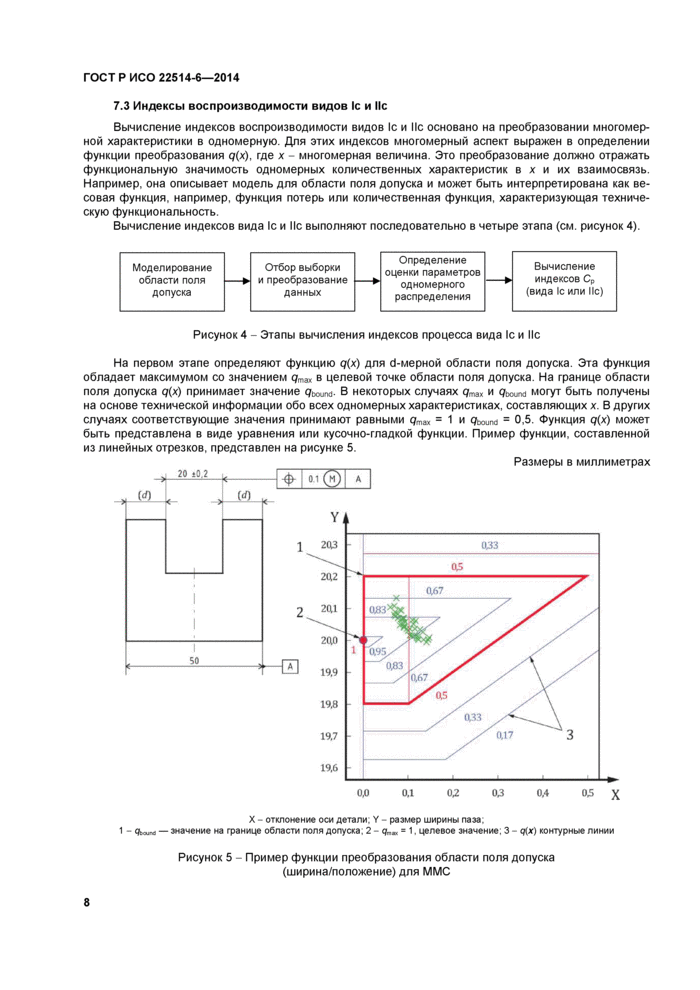
В таблице 1 приведены результаты измерений, выполненных на 100 деталях (положение отверстия и отклонение диаметра отверстия).
Результаты расчетов показаны на рисунке 8. Метод вычисления интервала изменчивости приведен в приложении А.
Количество измеренных деталей п = 100.
Установленные допуски: по оси X Lx = 79,750, Ux = 80,250.
по оси У Ly = -116,750, Uy = -116,250.
11
|
Таблица 1 — Результаты измерений и полученные отклонения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ГОСТ Р ИСО 22514-6-2014
|
Окончание таблицы 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
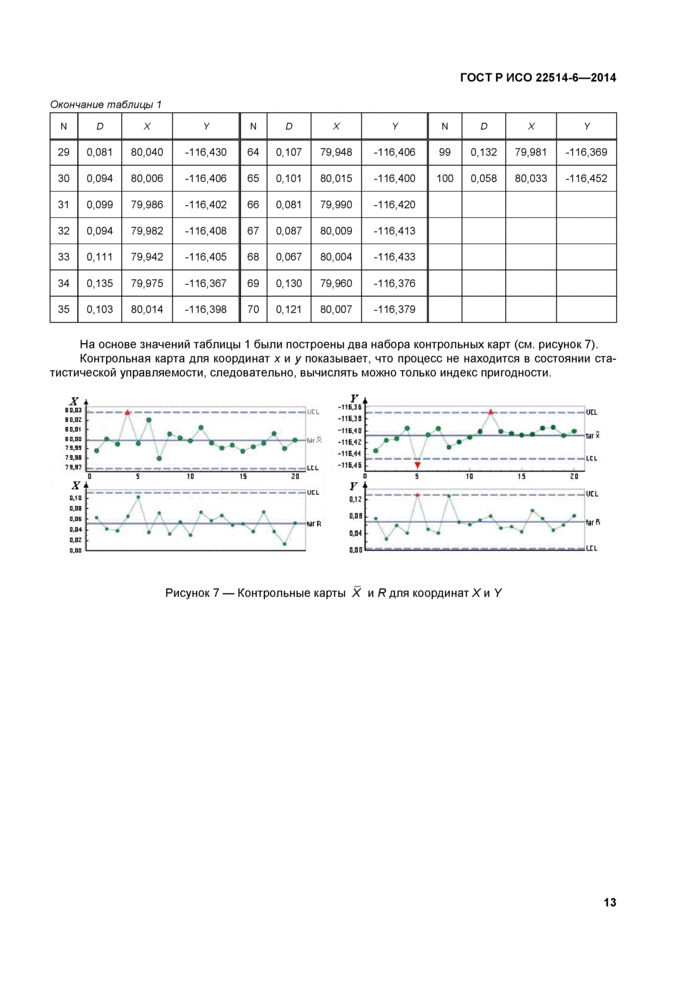
На основе значений таблицы 1 были построены два набора контрольных карт (см. рисунок 7). Контрольная карта для координат х и у показывает, что процесс не находится в состоянии статистической управляемости, следовательно, вычислять можно только индекс пригодности.
|
Рисунок 7 — Контрольные карты X и R для координат X и У |
13
и
|
У L U | |
|
У | |
|
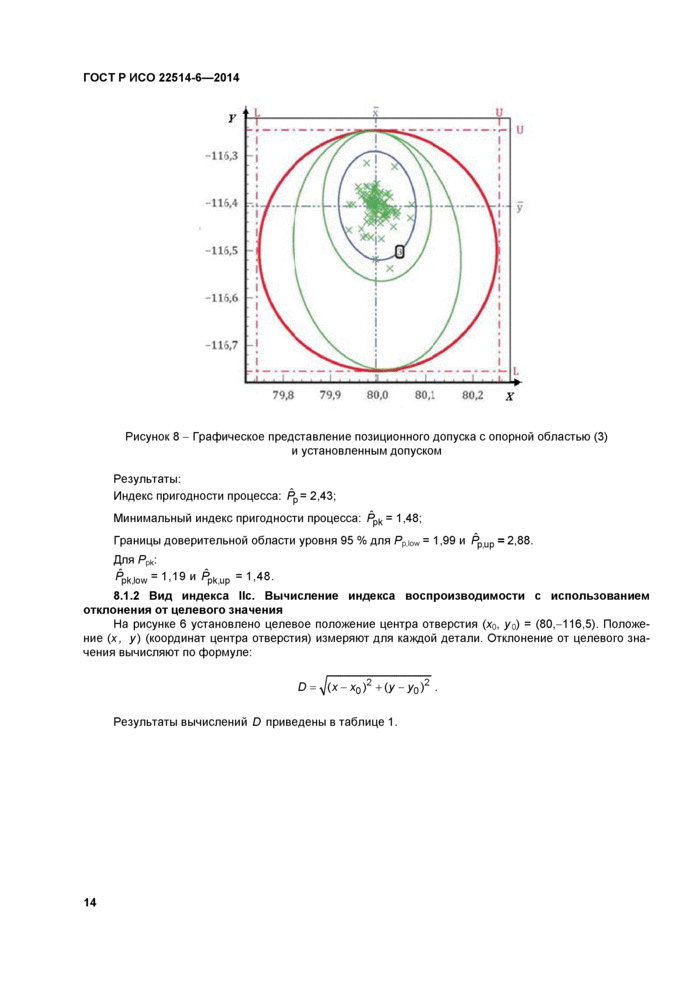
I - ■ ■ I ■ ■ =1 ■ ■ ■ ■ ' ■ ■ ' I ■ ■ ■■ ! 79,8 79,9 80,0 80,1 80,2 X Рисунок 8 - Графическое представление позиционного допуска с опорной областью (3) и установленным допуском | |
L
+■
Результаты:
Индекс пригодности процесса: Рр = 2,43;
Минимальный индекс пригодности процесса: Ррк = 1,48;
Границы доверительной области уровня 95 % для Рр |0W = 1,99 и Рр ир = 2,88. Для Ррк:
Ppk,iow = 1.19 и ^рк,up = 1'48-
8.1.2 Вид индекса Мс. Вычисление индекса воспроизводимости с использованием отклонения от целевого значения
На рисунке 6 установлено целевое положение центра отверстия (х0, у0) = (80,-116,5). Положение (х, у) (координат центра отверстия) измеряют для каждой детали. Отклонение от целевого значения вычисляют по формуле:
Результаты вычислений D приведены в таблице 1.
14ГОСТ Р ИСО 22514-6-2014
|
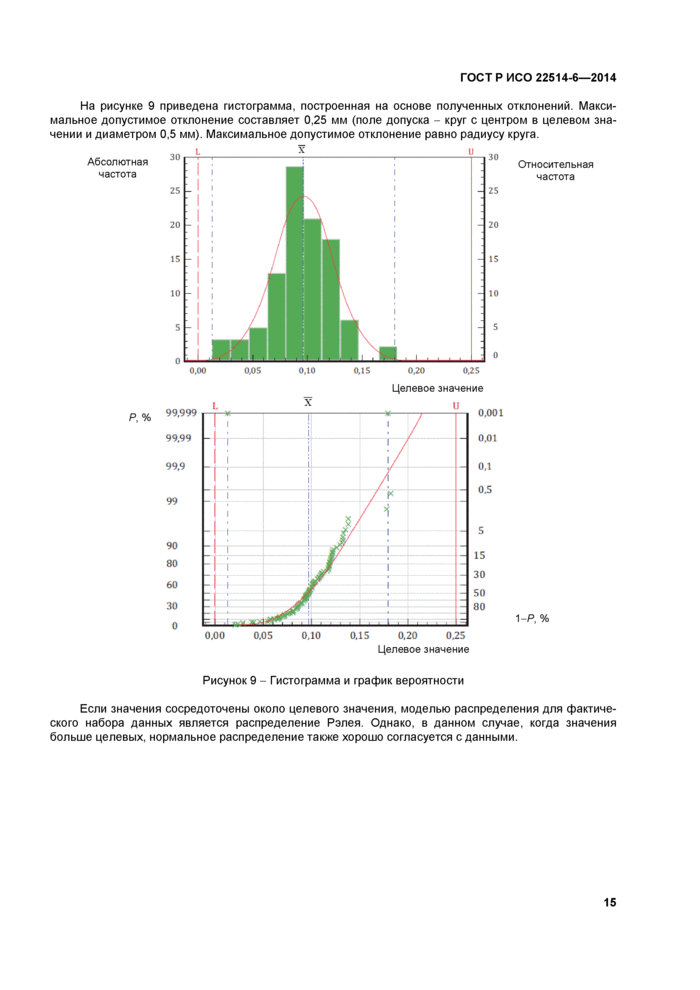
На рисунке 9 приведена гистограмма, построенная на основе полученных отклонений. Максимальное допустимое отклонение составляет 0,25 мм (поле допуска - круг с центром в целевом значении и диаметром 0,5 мм). Максимальное допустимое отклонение равно радиусу круга. |
|
Целевое значение |
|
Рисунок 9 - Гистограмма и график вероятности |
Если значения сосредоточены около целевого значения, моделью распределения для фактического набора данных является распределение Рэлея. Однако, в данном случае, когда значения больше целевых, нормальное распределение также хорошо согласуется с данными.
15
|
UCL tar х LCL |
|
UCL tar R | |
|
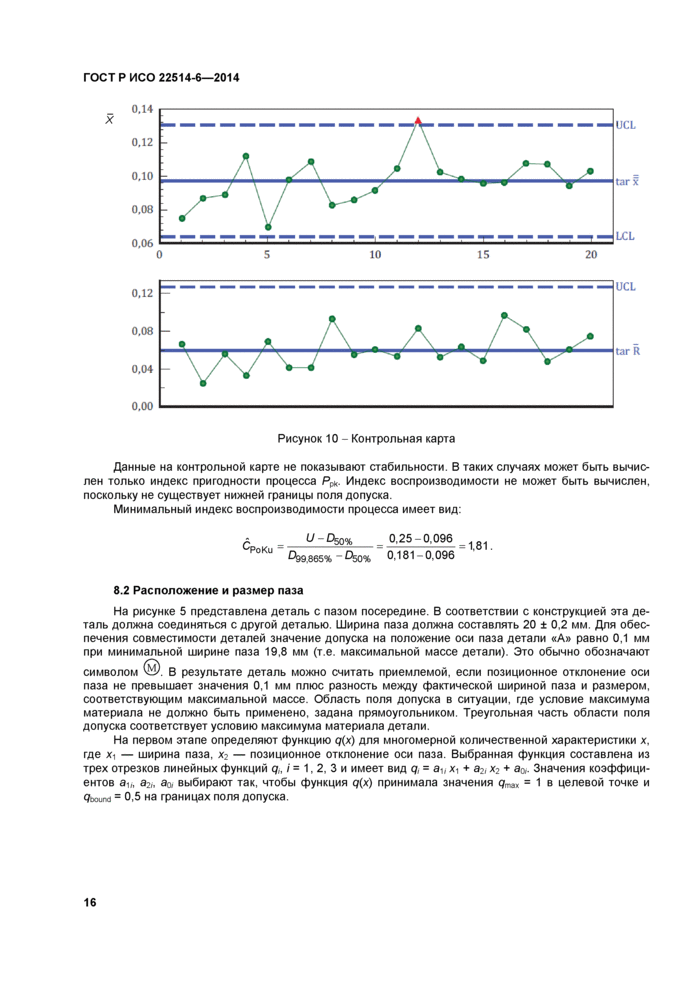
Рисунок 10 - Контрольная карта | |
Данные на контрольной карте не показывают стабильности. В таких случаях может быть вычислен только индекс пригодности процесса Ррк. Индекс воспроизводимости не может быть вычислен, поскольку не существует нижней границы поля допуска.
Минимальный индекс воспроизводимости процесса имеет вид:
А _ U-D50% _ 0,25-0,096 ,Q,
vpni/|, — - — - — 1,0 I .
^9,865%-%)% 0,181-0,096
8.2 Расположение и размер паза
На рисунке 5 представлена деталь с пазом посередине. В соответствии с конструкцией эта деталь должна соединяться с другой деталью. Ширина паза должна составлять 20 ± 0,2 мм. Для обеспечения совместимости деталей значение допуска на положение оси паза детали «А» равно 0,1 мм при минимальной ширине паза 19,8 мм (т.е. максимальной массе детали). Это обычно обозначают
символом @. В результате деталь можно считать приемлемой, если позиционное отклонение оси паза не превышает значения 0,1 мм плюс разность между фактической шириной паза и размером, соответствующим максимальной массе. Область поля допуска в ситуации, где условие максимума материала не должно быть применено, задана прямоугольником. Треугольная часть области поля допуска соответствует условию максимума материала детали.
На первом этапе определяют функцию q(x) для многомерной количественной характеристики х, где х1 — ширина паза, х2 — позиционное отклонение оси паза. Выбранная функция составлена из трех отрезков линейных функций qr,-, / = 1,2, 3 и имеет вид q, = а1, х1 + а2,х2 + а0/. Значения коэффициентов а1(, а2/, а0, выбирают так, чтобы функция q(x) принимала значения qmax = 1 в целевой точке и (/bound = 0,5 на границах поля допуска.
ГОСТ Р ИСО 22514-6-2014Содержание
1 Область применения.....................................................................................................................................1
2 Нормативные ссылки.....................................................................................................................................1
3 Термины и определения...............................................................................................................................1
4 Сокращения и обозначения..........................................................................................................................3
5 Анализ процесса............................................................................................................................................3
6 Использование многомерных индексов воспроизводимости и пригодности процесса..........................4
7 Вычисление индексов воспроизводимости и пригодности процесса.......................................................4
8 Примеры.......................................................................................................................................................11
Приложение А (справочное) Обоснование использованных формул......................................................20
Приложение В (справочное) Пример оценки воспроизводимости для дисбаланса оси.........................24
Приложение С (справочное) Пример оценки воспроизводимости для позиционного отклонения
оси отверстия.......................................................................................................................29
Приложение D (справочное) Построение функции качества.....................................................................32
Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов
ссылочным национальным стандартам Российской Федерации....................................33
Библиография.................................................................................................................................................34
|
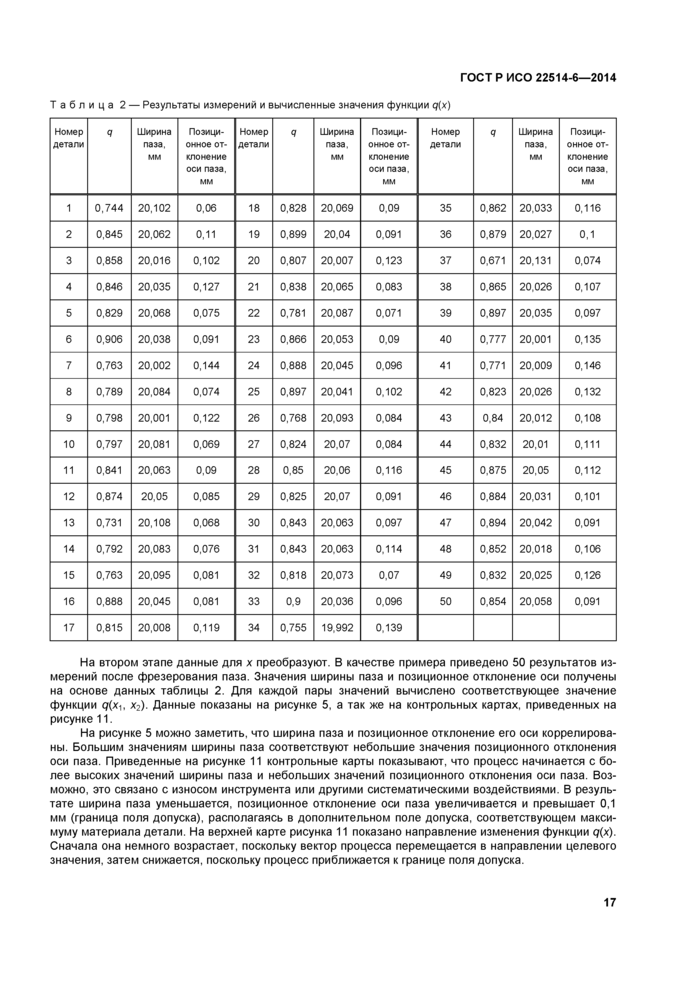
Таблица 2 — Результаты измерений и вычисленные значения функции q(x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
На втором этапе данные для х преобразуют. В качестве примера приведено 50 результатов измерений после фрезерования паза. Значения ширины паза и позиционное отклонение оси получены на основе данных таблицы 2. Для каждой пары значений вычислено соответствующее значение функции q(xb х2). Данные показаны на рисунке 5, а так же на контрольных картах, приведенных на рисунке 11.
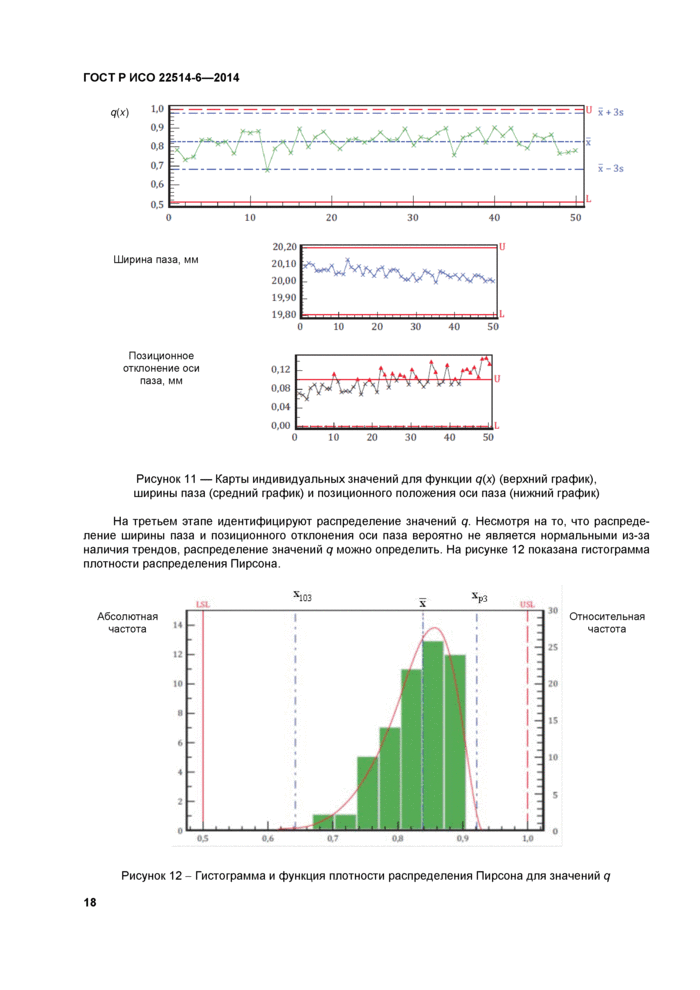
На рисунке 5 можно заметить, что ширина паза и позиционное отклонение его оси коррелирова-ны. Большим значениям ширины паза соответствуют небольшие значения позиционного отклонения оси паза. Приведенные на рисунке 11 контрольные карты показывают, что процесс начинается с более высоких значений ширины паза и небольших значений позиционного отклонения оси паза. Возможно, это связано с износом инструмента или другими систематическими воздействиями. В результате ширина паза уменьшается, позиционное отклонение оси паза увеличивается и превышает 0,1 мм (граница поля допуска), располагаясь в дополнительном поле допуска, соответствующем максимуму материала детали. На верхней карте рисунка 11 показано направление изменения функции qr(x). Сначала она немного возрастает, поскольку вектор процесса перемещается в направлении целевого значения, затем снижается, поскольку процесс приближается к границе поля допуска.
17
Введение
Возрастание сложности производственных методов и требований к качеству продукции и процессов, проводит к тому, что анализа процесса на основе измерений одномерных характеристик в некоторых случаях недостаточно и необходимо анализировать процесс на основе многомерных характеристик продукции. Это могут быть наблюдения сразу за несколькими геометрическими допусками или за динамическими величинами, такими как дисбаланс, или при наличии корреляции между характеристиками продукции.
По аналогии с ИСО 22514-21’ в настоящем стандарте приведены формулы для индексов воспроизводимости и пригодности процесса, которые расширяют понятия изменчивости и положения процесса на случай многомерных характеристик. Предложенные индексы основаны на классических индексах Ср и Сркдля одномерного случая. Необходимые объяснения расширения приведены в приложении А.
Приведены примеры возможного применения таких индексов в случае двумерных или трехмерных характеристик положения, дисбаланса или нескольких коррелированных характеристик химической продукции.
Разброс результатов измерений характеристик готовой продукции зависит от разброса параметров процесса изготовления продукции и точности процесса измерений. Предполагается, что воспроизводимость используемой измерительной системы подтверждена до определения воспроизводимости процесса изготовления продукции.
Метод вычислений, установленный в настоящем стандарте, следует использовать для принятия однозначного решения в следующих ситуациях:
- предельные значения индексов воспроизводимости процесса для многомерных, непрерывных количественных характеристик продукции должны быть установлены в контракте между заказчиком и поставщиком;
- необходимо сравнить возможности различных конструкций, производственных методов или поставщиков;
- необходимо провести одобрение производственного процесса;
- необходимо провести анализ и принять решение при наличии претензий или нанесения ущерба .
Примечание - Процессы создания продукции включают, например, производственные процессы, процессы обслуживания и сборки.
11 ИСО 22514-2:2013 Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 6. Возможности и характеристики моделей процессов, зависимых от времени.
IV
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы УПРАВЛЕНИЕ ПРОЦЕССАМИ Часть 6
Статистики воспроизводимости процесса для многомерного нормального распределения
Statistical methods. Process management. Part 6. Process capability statistics for multivariate normal distribution
Дата введения — 2015—12—01
1 Область применения
Настоящий стандарт устанавливает методы вычисления статистик воспроизводимости и пригодности процессов для многомерных количественных характеристик, в тех случаях, когда необходимо (или выгодно) рассматривать набор одномерных характеристик. Методы, приведенные в настоящем стандарте, разработаны на основе двумерного нормального распределения.
Примечание — Методология настоящего стандарта может быть применена также в случае многомерного распределения.
В стандарте не рассмотрены оценки различных методов в различных ситуациях и возможное применение каждого метода. В каждом случае выбор метода осуществляет пользователь на основе своих предпочтений.
Целью настоящего стандарта является установление различных способов вычисления индексов воспроизводимости и пригодности в случае сложных процессов или многомерных количественных характеристик продукции
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 22514-1 Статистические методы в управлении процессами. Воспроизводимость и пригодность.Часть 1. Основные принципы (ISO 22514-1 Statistical methods in process management - Capability and performance - Part 1: General principles and concept)
ИСО 22514-2 Статистические методы в управлении процессами. Воспроизводимость и пригодность.Часть 2. Пригодность и воспроизводимость процессов зависящих от времени (ISO 22514-2 Statistical methods in process management - Capability and performance - Part 2: Process capability and performance of time-dependent process models)
3 Термины и определения
В настоящем стандарте применены термины по ИСО 22514-1 и ИСО 22514-2, а также следующие термины с соответствующими определениями.
3.1 величина (quantity): Свойство материального объекта или явления, которое может быть выражено в виде числа или соотношения.
[Руководство ИСО/МЭК 99:2007, 1.1]
Издание официальное
3.2 многомерная величина (multivariate quantity): Набор величин, характеризующих свойства объекта.
Примечание 1- Набор может быть d-компонентным, то есть упорядоченным набором, состоящим из d элементов.
Примечание 2 - Если х, единичная характеристика набора, где / = 1, 2... d, то вектор х = (xi, Хг, ... Xd)J представляет собой многомерную величину. Таким образом, многомерную величину можно рассматривать как вектор характеристик продукции. Значение многомерной величины может быть представлено точкой в d-мерном пространстве.
Примечание 3 - Формирование многомерной величины в виде вектора выполняют на основе технических соображений.
Примечание 4 - Все одномерные величины, объединенные в многомерный вектор, должны быть измеримы на одном и том же объекте или единице продукции.
Примечание 5 - Если многомерная величина должна быть описана с помощью статистик, то вектор х = (хь х2,... xd) следует рассматривать, как случайный вектор, подчиняющийся d-мерному распределению.
Пример 1 — Пусть имеются три характеристики объекта xi — цвет, Хг — масса и х3 -число дефектов. Эти характеристики могут быть объединены в трехмерную величину для оценки процесса. Размерность вектора равна трем, d =3.
Пример 2 — Необходимо оценить положение оси ствола скважины при бурении шахты. Положение оси ствола определяется координатами х и у. Координаты могут быть объединены в двумерную величину х, у которой компонент xi является абсциссой, а хг — ординатой.
Пример 3 -Дисбаланс колеса.
3.3 поле допуска (tolerance region): Совокупность всех допустимых значений величины (3.2).
Примечание 1 — Поле допуска представляет собой область d-мерного пространства, которая может быть ограничена линиями, поверхностями или гиперповерхностями и не обязательно является закрытой. Форма и размеры области поля допуска могут быть определены одним или несколькими параметрами.
Примечание 2 - Типичные формы области поля допуска в двухмерном случае — прямоугольник, эллипс (или окружность), в трехмерном случае — куб или эллипсоид, в многомерном случае — гиперкуб, гиперэллипсоид или сложные призматические формы. На рисунке 1 показаны примеры областей поля допуска в двухмерном пространстве.
Примечание 3 — Поле допуска зависит от требований к продукции. Если значение характеристики находится вне поля допуска, то предполагается, что продукция не соответствует установленным требованиям. (Такая продукция является несоответствующей).
Примечание 4 — При проверке положения характеристики продукции по отношению к области поля допуска порядок единичных характеристик в многомерной характеристике и ее размерность должны быть такими же, как при формировании области поля допуска.
Пример - Определение «поле допуска» по стандарту ИСО 1101 для геометрических размеров можно применить к понятию «области поля допуска». В этом случае геометрические линии или поверхности, соответствующие границам поля допуска, формируют область поля допуска.
2
ГОСТ Р ИСО 22514-6-2014
X,
X,
А) В) С)
А - область поля допуска в виде прямоугольника с параметрами аг а,, х и у ;
В - область поля допуска в виде окружности с параметрами d, х и у ;
С - область поля допуска в виде трапеции с параметрами av з2, Ь, х и у
Рисунок 1 - Примеры областей поля допуска в двухмерном пространстве для двумерной величины (х-i, х2)т
3.4 показатель воспроизводимости процесса (process capability): Статистический показатель, определяемый на основе выходной характеристики процесса (3.1), по которому судят о нахождении процесса в состоянии статистической управляемости, позволяющий оценить способность процесса поддерживать выходную характеристику процесса в соответствии с установленными для нее требованиями.
Примечание 1 - Индекс воспроизводимости процесса характеризует способность процесса обеспечивать установленные требования
Примечание 2 - Индекс воспроизводимости обозначают Ср.
3.5 оценка воспроизводимости процесса (estimated process capability): Оценка показателя воспроизводимости процесса (3.4), полученная с помощью статистических методов.
3.6 показатель пригодности процесса (process performance): Статистический показатель, определяемый на основе выходной характеристики процесса, используемый для описания процесса, пребывание которого в состоянии статистической управляемости не подтверждено.
3.7 оценка пригодности процесса (estimated process performance): Оценка показателя пригодности процесса (3.6), полученная с помощью статистических методов.
4 Сокращения и обозначения
ММС - условие максимума материала;
PCI - индекс воспроизводимости процесса ((',,).
5 Анализ процесса
Цель анализа процесса состоит в получении достоверной информации о процессе. Эта информация необходима для эффективного управления процессом, т.е. управления, обеспечивающего соответствие продукции, изготовленной процессом, требованиям к ее качеству.
Анализ процесса представляет собой анализ одной или нескольких характеристик, наиболее важных для процесса.
Вместо характеристик процесса часто анализируют характеристики продукции, поскольку характеристики продукции характеризуют не только продукцию, но и процесс, изготавливающий эту продукцию.
3
Величины, используемые для анализа, как правило, определяют на основе выборок, отобранных в процессе выполнения технологических операций. Объем выборки и частоту отбора выборок определяют в зависимости от особенностей процесса и продукции так, чтобы все важные изменения были обнаружены вовремя. Выборки многомерных количественных характеристик, используемые для анализа процесса должны быть представительными. (Одномерные статистики рассмотрены в ИСО 22514-2.) В настоящем стандарте для анализа воспроизводимости процесса рассмотрены многомерные статистики.
Для определения оценок Ср желательно, чтобы объем выборки был не менее 125.
6 Использование многомерных индексов воспроизводимости и пригодности процесса
Целью определения индекса воспроизводимости процесса является определение того, насколько хорошо (или плохо) процесс может изготавливать продукцию, соответствующую установленным требованиям. Использование Ср для многомерных характеристик позволяет сделать это лучше, чем Ср для одномерных характеристик.
Так как существует несколько определений многомерного Ср, то выбор окончательного варианта определяет пользователь. Ниже приведены рекомендации по использованию многомерного индекса
сР.
Использование многомерной оценки воспроизводимости и пригодности процесса является предпочтительным, если:
- многомерная оценка позволяет описывать воспроизводимость и пригодность процесса одной статистической величиной вместо большого количества одномерных характеристик;
- границы поля допуска не могут быть определены для каждой характеристики независимо одна от другой (обычно так бывает, если область поля допуска имеет форму, отличную от прямоугольника или многомерного параллелепипеда);
- одномерные характеристики коррелированы между собой.
Пример — Двумерное поле допуска положения оси ствола скважины. Область поля допуска имеет вид круга с определенными размерами по оси х и оси у (см. 8.1.) Результатом измерения положения оси отверстия скважины являются координаты точки (х, у). Гоаницы поля допуска по координате х не могут быть выражены независимо от координаты у. Таким образом, должна быть применена двумерная оценка.
7 Вычисление индексов воспроизводимости и пригодности процесса
7.1 Описание индексов вида I и II
Для многомерных количественных характеристик существуют разные подходы к определению воспроизводимости и пригодности процесса. В настоящем стандарте приведено описание двух различных видов индексов: вида I и вида II. Различие видов индексов состоит в способе их определения (вероятностном или геометрическом).
Применяют следующие определения вида индекса:
- Индекс вида I, основанный на вероятности Р соответствия (или несоответствия) продукции установленным требованиям, вычисляют как отношение индекса и вышеупомянутой вероятности в случае одномерного нормального распределения.
- Индекс вида II вычисляют как отношение площади или объема области поля допуска к площади или объему области изменчивости процесса.
По практическим соображениям в настоящем стандарте использовано многомерное нормальное распределение. Однако, существуют ситуации, в которых необходимо использовать другие распределения. Кроме того, по тем же соображениям, в настоящем стандарте область изменчивости процесса выбрана в форме эллипсоида.
Наиболее важные свойства многомерного нормального распределения приведены в приложении А.
Чтобы сделать область изменчивости процесса сопоставимой с областью поля допуска обычно используют дополнительные преобразования. Существуют три вида преобразований:
а) преобразование области поля допуска в область изменчивости процесса;
b) преобразование области изменчивости процесса в область поля допуска;
c) преобразование области поля допуска и/или области изменчивости процесса в другую область в соответствии с функцией количественной характеристики процесса.
Для определения многомерного Ср виды индексов и преобразований могут быть объединены. Однако не любая комбинация может быть использована. Например, не существует индекса Ср, объединяющего индекс вида I и преобразование Ь).
Термин «воспроизводимость» может быть использован только по отношению к процессам, для которых с помощью контрольных карт было продемонстрировано, что они находятся в состоянии статистической управляемости. Если для процесса не было продемонстрировано, что он находится в состоянии статистической управляемости, то по отношению к нему может быть использован только термин «пригодность».
7.2 Обозначения индексов
7.2.1 Общие положения
В настоящее время используют различные обозначения для индексов воспроизводимости и пригодности. Эти обозначения должны позволять определить вид индекса или область его применения. Для того, чтобы различать индексы воспроизводимости и пригодности используют символы С (capability) для индексов воспроизводимостей и Р (perfomance) для индексов пригодности. В стандартах ИСО 22514 использованы обозначения Ср и/или Срк, Рр и/или Ррк.
7.2.2 Индекс воспроизводимости процесса
Рассмотрим d-мерное нормальное распределение /Vd(p, Е) с вектором средних р и матрицей ковариации Е. Если область изменчивости не имеет овальную форму (не представляет собой окружность, эллипс, если d = 2 или сферу, эллипсоид, если d = 3 или гиперсферу, гиперэллипсоид, если d > 3), она должна быть преобразована в область поля допуска, которая имеет овальную форму. Преобразование выполняют таким образом, чтобы область изменчивости процесса была наибольшей из возможных (самый большой эллипс, эллипсоид или гиперэллипсоид) и целиком вписывалась в область поля допуска.
Для вычисления многомерного индекса Ср нормальное распределение должно быть таким, чтобы среднее значение находилось в центре овальной области поля допуска. Для такого нормального распределения определяют наибольший контур эллипсоида, который полностью содержится в овальной области поля допуска, и вычисляют вероятность попадания характеристики в объем, ограниченный этим эллипсоидом в случае d-мерного нормального распределения с матрицей ковариации I и средним в центре овальной области поля допуска. Обозначим эту вероятность Р, тогда многомерный индекс Ср вычисляют по формуле:
Вычисление вероятности Р реализации наблюдений х внутри эллипса (эллипсоида/ гиперэллипсоида) для любого значения d может быть сделано с использованием функции распределения. Более подробные пояснения приведены в А.1 приложения А.
Для определения оценки индекса Ср по d-мерным данным определяют ковариационную матрицу многомерного нормального распределения. Используют оценку ковариационной матрицы £ для определения контура эллипсоида и соответствующей ему вероятности Р. Оценка многомерного индекса Ср имеет вид:
5
|
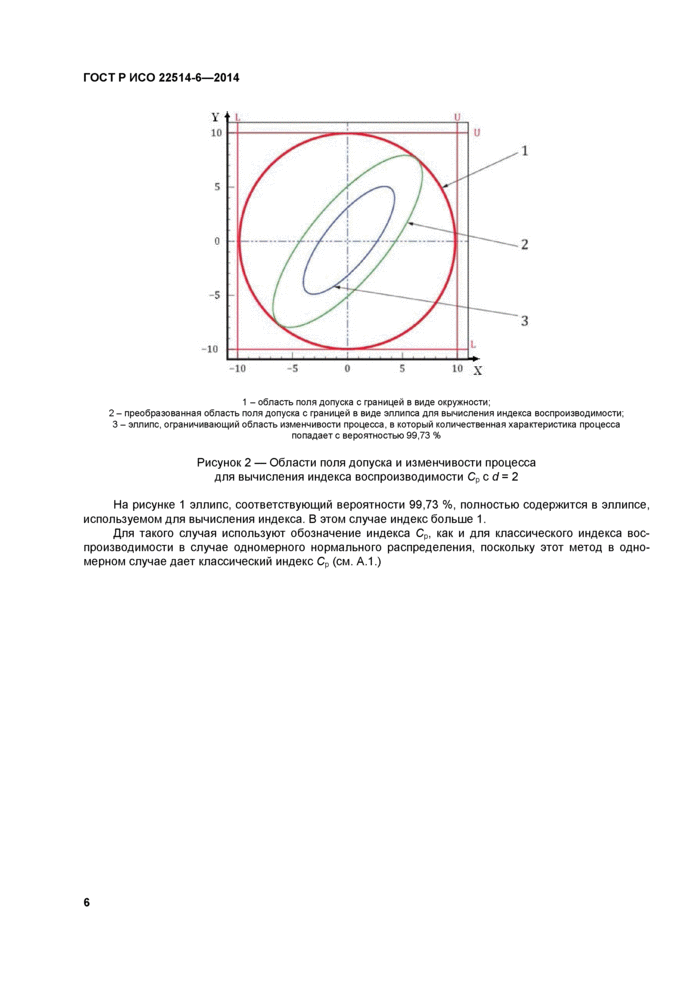
1 - область поля допуска с границей в виде окружности; 2- преобразованная область поля допуска с границей в виде эллипса для вычисления индекса воспроизводимости; 3 - эллипс, ограничивающий область изменчивости процесса, в который количественная характеристика процесса попадает с вероятностью 99,73 % |
Рисунок 2 — Области поля допуска и изменчивости процесса для вычисления индекса воспроизводимости Ср с d= 2
На рисунке 1 эллипс, соответствующий вероятности 99,73 %, полностью содержится в эллипсе, используемом для вычисления индекса. В этом случае индекс больше 1.
Для такого случая используют обозначение индекса Ср, как и для классического индекса воспроизводимости в случае одномерного нормального распределения, поскольку этот метод в одномерном случае дает классический индекс Ср (см. А.1.)
6