Р 50-54-42-88
Расчеты и испытания на прочность. Метод конечных элементов и программы расчета на ЭВМ пространственных элементов конструкций в упругопластичной области деформирования
Купить Р 50-54-42-88 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Рекомендации распространяются на расчет методом конечных элементов пространственных объектов, подвергаемым статическим термосиловым нагрузкам при смешанных граничных условиях в упругопластической области деформирования.
Дефект оригинала
Оглавление
1. Принятые обозначения и сокращения
2. Постановка задачи
2.1. Соотношения пространственной задачи термоупругости
2.2. Основные гипотезы термопластичности. Уравнения состояния
3. Метод решения
3.1. Метод конечных элементов для решения пространственных задач термопластичности
3.2. Библиотека конечных элементов ППП "Куб"
3.3. КЭ в форме косоугольного параллелепипеда
3.4. Изопараметрический криволинейный КЭ
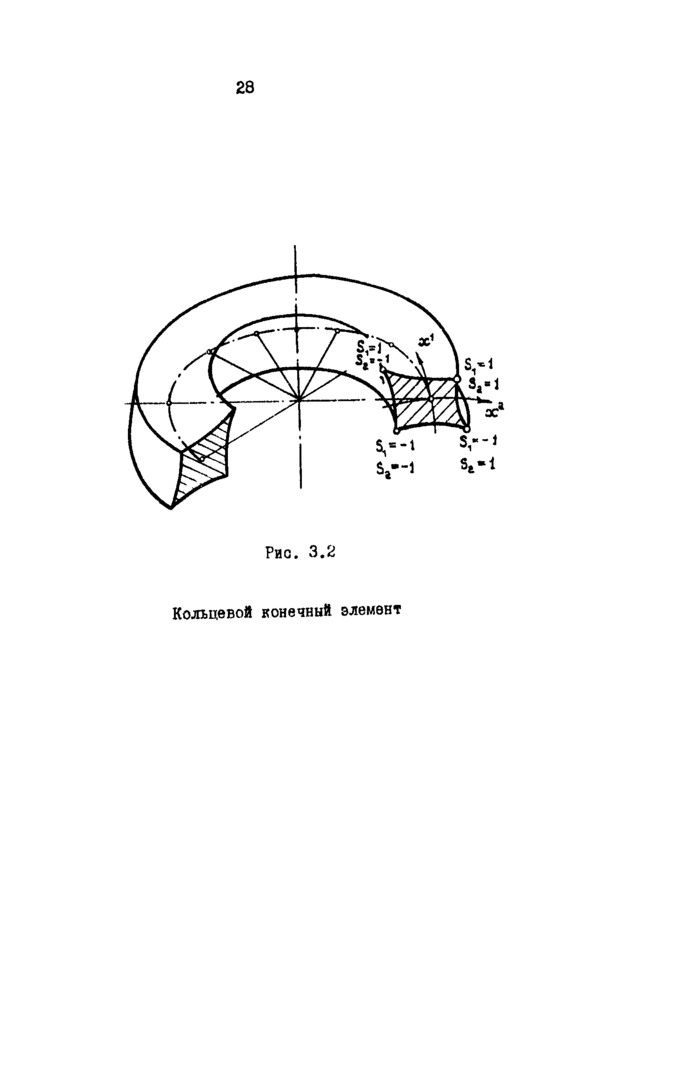
3.5. Кольцевой КЭ ППП "Круг"
4. Алгоритмы решения, перечень исходных данных и получаемых результатов
4.1. Алгоритмы решения системы нелинейных уравнений
4.2. Исходные данные и получаемые результаты
5. Приложения
5.1. Пояснительная записка
5.2. Теоретическое обоснование МСКЭ
5.3. Вывод узловых реакций и матрицы жесткости неоднородного замкнутого кольцевого конечного элемента ППП "Круг"
5.4. Программная документация
5.5. Примеры расчета
Литература
| Дата введения | 03.09.1987 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот документ находится в:
Организации:
| 03.09.1987 | Утвержден | ВНИИНМАШ | 274 |
|---|---|---|---|
| Разработан | ВНИИНМАШ | ||
| Разработан | Киевский ордена Трудового Красного Знамени инженерно-строительный институт |
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9
стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19
стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26

стр. 27

стр. 28
стр. 29

стр. 30
|
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ |
РАСЧЕТЫ
И ИСПЫТАНИЯ НА
i@t
ПРОЧНОСТ1
Il€ У ДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ (Госстандарт СССР)
Всесоюзный научно-исследовательский институт по нормализации в машиностроении (ВНИИШШ1)
Утверждены
Приказом ВНИИНМАШ » 2?4 от 03.5Л96Г7Г,
Расчеты и испытания на прочность
Метца ко печных элементов и программы расчета на ЭШ пространственных элементов конструкций в упругопластической области деформирования
Рекомендации Р 50-54-42-88
10
2,1,9. Компоненты тензора напряжений в упругой области деформирования определяются через компоненты тензора деформаций яри помощи обобщенного закона Гука [241 :
&iJ- C'-JKt6Ke. (2.14)
Для изотропного тела компоненты тензора упругих постоянных CtJK^ выражаются через коэффициенты Ламе Я ж i; , в общем случае зависящие от температуры,
кг
J
'■ ?и »
/Г
(2.15)
где
2 =
_Е_ $__
(Я-20)(^9)
В
С~Е(Т) ,$‘д(Т) - значение модуля Юнга и коэффициента Пуаооона при заданной температуре.
2.2. Основные гипотезы термопластичности. Уравнения состояния
2.2.1, Зависимость между напряжениями и деформациями эа пределом упругости устанавливается на основе уравнений теории течения. Предполагается, что упругие свойства и диаграмме деформирования материала зависят от температуры.
2.2.2. Теория пластического течения о изотропным упрочнением при яензотермичеохях процеооях нагружения базируетоя на следующих основных принципах [II,16] .
I. Материал тела однородный и изотропный, изменение его обьеме линейно-упругое;
II
P
(2.16)
£к« - Ot
2. Компоненты тензора приращений полных деформаций cf£\j
состоят из приращений упругих , пластических йсч
т
и температурных d£tj / составляющих
cLt,] = d£tj + d£?j d£cj. (2.i7)
Приращения температурных деформаций определяются выражениями
[24J
d£[j = drdTfycj f (2.18)
где dT-dr(T) - значения коэффициентов линейного теплового расширения при заданной температуре, cJT - приращение температуры в данной точке.
3. Область упругих деформаций при активном нагружении для любого напряженного состояния в пространстве напряжений ограничивается поверхностью нагружения
f(FL', а?, т)*о9 (2.19)
где 3? - параметр пластичности Одквиста. Функция текучести / характеризует переход материала из упругого ооотоявия в пластическое. В частности, при £ < 0 - материал деформируется по упругому закону, при / =0 наступает состояние текучеотн.
Принято, что состояния / > 0 не может быть реализовано.
4. В случае ассоциированного закона пластнчеокого течения компоненты тензора приращений плаотичеокой деформации пропорциональны производным функции текучести по компонентам тенвора напряжений:
p
(2.20)
d£^j - dj Qj$)
где dJ. - некоторый неопределенный не отряда тельный скалярный
множитель. Соотношения (2.20) означают, что пластическое течение развивается по нормали к поверхности текучести.
2.2.3. Принимая гипотезу изотропного упрочнения [II], уравнение поверхности нагружения при условии текучести Мизеоа запишем в виде
(2.21)
|
slj .= - ■* &**.} |
где Zs - предел текучести при чиотом одвиге, SLJ - компоненты девиатора напряжений:
(2.22)
(2.23)
2.2.4. Принимается ассоциированный закон пластического течения. Тогда на основании (2.20) компоненты тензора приращений пластических деформаций однозначно связаны о компонентами девиатора напряжений соотношениями
(2.24)
13
2.?.5. В случае яеизотермического процесса деформировался принимаются предпосылки о функциональных зависимостях
- f?s (Я?> Т) I
(2.25)
ЗБ - JVj бЬр> d£° .
Для определения закона ооотояния необходимо для каждого конкретного материала задать скалярную функцию Ts , зависящую от па-раметра & , фиксирующего иоторию нагружения, и температуры ГГ,
2.2.6. Установим зависимость между приращениями напряжений и пластических деформаций.
Поскольку при пластическом деформировании изображающая точка остается на поверхности нагружения, выполняется равенство
di - <**' ' %- ЧГ ' Ц в» -О. <2.26,
Для принятой поверхности нагружения (2.21)
df = S,j dSiJ - dT + 0 dzbo. (2.27)
С учетом иввеотного соотношения
Slj dSLj-- SLJ d^d (2.28)
|
перепишем (2.27) в виде | |
|
(2.29) | |
Из (2.25) о учетом (2.24) и (2.21) получим
V. wo -
аде = у ал ь s.
Подставив (2.30) в (2.29), найдем неопределенный множитель йл
аз. , (г-31)
(Г
где обозначено:
(2.30)
/ г L/lfS* д t-s
г ~ чь LS + т ^ ^ ,
о
5
(2.32)
Тогда связь между приращениями напряжений и деформаций представляется в виде
d^j = с *l(d£*e - d£h) -(рч- QL/) dr, (2.зз)
где введены следующие обозначения:
q mt £ijnt
rLJ r*£
~y—
(2.34)
= 2&5n •
dCLj*e
(2.35)
PLJ=
dT
£tc , QV.itpL.. ) ^
15
3. МЕТОД РЕШЕНИЯ
3.1. Метод конечных элементов для решения пространственных задач термоплаотичности
Метод конечных элементов (МКЭ) [ 10J эффективен при решении широкого круга краевых эадач меха-ханики оплошной среды. Одним из направлений развития МКЭ является распространение на физически нелинейные задачи. В данной работе рассматривается подход^ основании^ на методе переме-щений^н его применение к исследованию упругопластического деформирования пространственных конструкций. Вывод уравнений для конечных элементов и их объединение в систему уравнений осуществляется на основе вариационных методов. Предлагаемая схема вывода соотношений МКЭ [21,22] позволяет учеоть основные свойства жестких смещений для язопараметрических конечных элементов, компоненты деформации которых зависят от производных жестких вращений и от поступательных и вращательных смещений каждого элемента в целом, и извеотна как монентная схема конечных элементов (МСКЭ).
Процесс решения задач механики твердого тела по МКЭ состоит из следующих этапов:
1) дискретизация области на конечные элементы;
2) введение интерполяционных функций, т.е. аппроксимация ноля перемещений внутри конечного элемента через значения перемещений в узлах элемента;
3) вывод уравнений для каждого элемента;
4) объединение уравнений элементов в единую систему для всей рассматриваемой области;
5) решение общей системы уравнений;
16
6) вычисление искомых полей перемещений и напряжений.
5 предлагаемых рекомендациях рассматриваются в основном второй, третий и пятый этапы. При этом учитывают, что имеют* ся фундаментальные разработки метода конечных элементов^ 10,24]
Принципы и ооновные положения МСКЭ изложены в Приложении.
3.2. Библиотека конечных элементов ППП "Куб"
3.2.1. Для обеспечения проотрвнотвенных расчетов в ПИП "Куб" применяются различные типы КЭ в зависимости от геометрической сложности конструкции, ресурсов машинного времени, оперативной и дисковой памяти.
3.2.2. Для пространственных конструкций, объем которых
можно аппроксимировать конечными элементами прямолинейной формы, вводится предположение, что КЭ ввиду малости его размеров можно принимать в форме косоугольного параллелепипеда и подучат коэффициенты MS в аналитической форме. Для конструкции олокной формы с криволинейной границей возможно применение криволинейных КЭ в виде произвольных шестигранников о численным иитегри реваншем по объему элемента и аппроксимацией координат и перемещений с помощью полиномов Лпграпже от Г до 3-й степени по трем напревлгнипм и включает КЭ о полилинейной, поли-
квадратичной, нолику бичеокой ттрокоимипией и их комбинациями по раз.личным направлениям.
3. •!. 'К ''нойстта элемечт"в. Нччиодонт Mi элементов осум**
'•ГЧОО'М'Ч? п <nv>7f»ГНИЯ г r<\vi т >ПИ;?МИ W'’Q. Д.ЛН Я/РМСН ГОР •
17
численным интегрированием до объему вычисление коэффициентов выполняется по стандартным программам. Ш конечных элементов с аналитическим интегрированием вычисляются по отдельным программам. КЭ с аналитическим интегрирование по объему для вычисления коэффициентов Ш требует в шесть раз меньше времени, чем полилинейный элемент с численным интегрированием. Поэтому для тыл, близких к призматическим и с прямолинейными границами, можно рекомендовать применение КЭ о аналитическим интегрированием при незначительном сгущении сеточной области. Значительное сгущение сеточной области приводит к увеличению ширины строки ЫЖ, что ведет к увеличению времени вычисления U3K всей конструкции. Поэтому для трехмерных тел сложной формы с криволинейными границами следует применять криволинейные элементы о численным интегрированием.
3.2.4. Данные для элементов. Вое величины, относящиеся к элементам, могут быть переменными. Свойства материалов, нагрузки могут задаваться для групп элементов и зависят от номера узла, принадлежащего данному элементу.
3.3. КЭ в форме косоугольного параллелепипеда
З.ЗЛ. Конечные элементы в форме параллелепипеда (косоугольного и прямоугольного) имеют ту особенность, что метрические характеристики местной системы координат постоянны в объеме элемента и коэффициенты матрицы жесткости можно получить в замкнутой форме.
Предполагается, что компоненты тензора преобразования координат в объеме алемеита постоянны;
dzJ
dZJ>
dxL
(3.1)
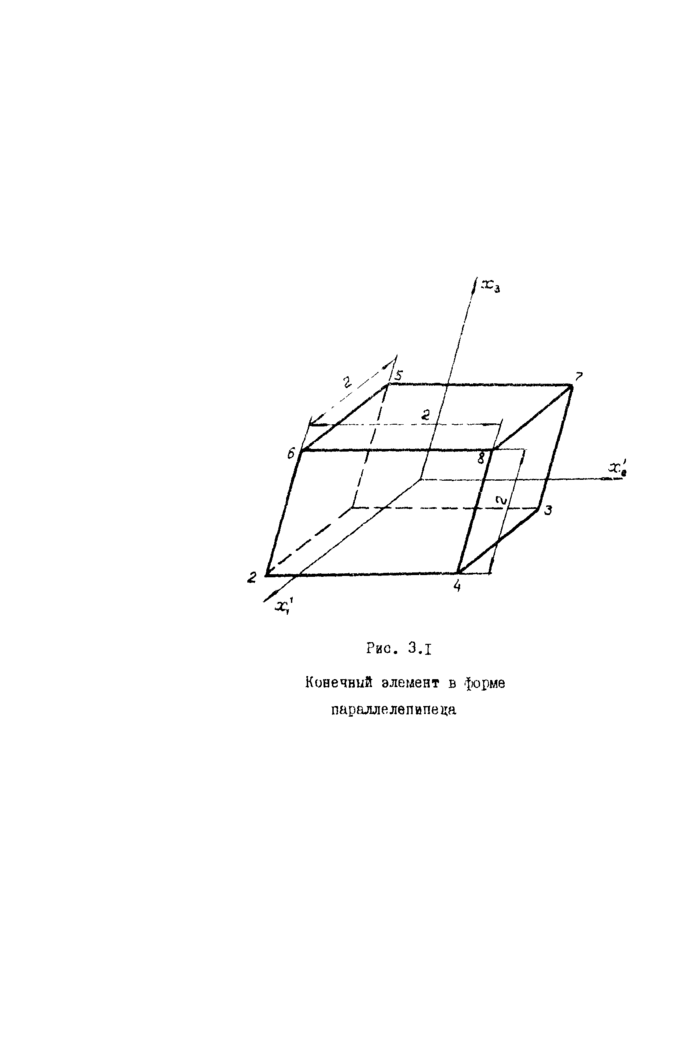
Конечннй элемент в форме коооугольного параллелештеда отобразим на куб о длиной ребра, равной 2. Местную онотему координат поместим в центр куба (рио.3.1). Перемещения точек КЭ предотавим вврахенкем
где
[Ят]г-[-ц-и-н~н];
[Рзт]Г^[Ч-4ЧЧНН];
т = 1,8 - яоквльннй номер уела.
Деформации еле ментов определяются по формулам
в, = / С?2 U” Pm (S+ ЯтХ*)(4+ Й>т X3);
(3.3)
fti- 4- cii и*йт(4+ OmX*)( 1 + й,тXs); f CXI и*'Рм(-?+ал>Х<)( 4 + втЯ*);
« да*/
= P & u* (* * Д,т&)(с?А» * cl'km);
UUi+&*&)(&'Am +C?Om);
) f ! С I / + Ptm X'XCl P3m + Cl Вт)
ff) " J
18
Xj-0 •
i
Рио. 3.1 Конечный элемент в форме
параллелепипеда
3
Группа T5I
УДК 539.3
РЕКОМЕНДАЦИИ
Расчета и испытания на прочность Метод конечных элементов и программы расчета на ЭВМ пространственных элементов конструкций в упругоплас-тической области деформирования
Р 50-54-42-88
ОКСТУ 4103
Рекомендации распространяются на расчет методом конечных элементов (МКЭ) пространственных объектов, подвергаемым статическим термосиловым нагрузкам при смешанных граничных условиях в упругопластической области деформирования.
Решение физически нелинейной задачи состоит в сведении краевой задачи к системе разрешающих нелинейных уравнений. Эффективность решения краевой задачи обеспечивается использованием моментной схемы конечных элементов ШСКЭ) [ 22J . При исследовании массивных и тонкостенных конструкций она не только превосходи^ другие варианты МКЭ, основанные на соотношениях теории упругости, но и не уступает оболочечным КЭ.
В рекомендациях предложен выбор оптимального алгоритма решения систем нелинейных уравнений, а также приведены г\лн определения точности получаемых результатов и затрп’ мо.инисто времени при использовании различных anr^ptrvon.
где u
где
20
вычисляется по (3.6).
Матрица жесткости КЭ представляется в вхде
&] * Ес &*'j1
'3*5 >
(3.4)
и
Коэффициенты матрицы хеотхоотх определяется по формулам
_ Г L pj/ Г'^
Ьтп ~ Ls it (Prnn 8
'■/
(3.5)
пппп
ЪРпт Fbn
(по м и п - ее суммировать!), где
лТи --(1- s;)(i - &")(/-%)0-8Г)-.
I'-il-In-, ц] --[ir-cosm.,пУ]>-ъ ■
Можно существенно уменьшить количество операций при вычис-
/, S ь
дзнян коэффициентов Ьтп , если развернуть произведения х сум мы но воем индексам.
3.4. Иэопараметрический криволинейный КЗ Рассмотрим процесс вывода Ш для криволинейного параллели иинеда. Считаем, что область 0, занимаемая элементом (рно.3.1) отображена на куб о ребрами единичной длины, внутренние оьойсг
4
Эффективность решения пространственной задачи неосесим-матричного упругошгастического деформирования тел вращения обеспечивается применением полуакалитического метода конечных элементов (ПМКЭ), основанного на представлении перемещений и внешних нагрузок отрезками ряда ^рье по окружной координате и конечноэлементной аппроксимации их в плоскости меридианаль-ного сечения.
Метод конечных элементов реализован в пакете прикладных программ (ППП): "Куб"- для расчета пространственных тел призматической формы (общего вида) и "Круг" - для расчета неосесимметрично нагруженных тел вращения. ППП разработаны в развитие системы "Прочность-75", сданной в Республиканский фонд алгоритмов и программ \20] . Апробированы на контрольных примерах, показывающих эффективность метода и достоверность получаемых результатов при решении сложных задач упругопластического деформирования ответственных машиностроительных конструкций.
Подлинники программ хранятся в Киевском ордена Трудового Красного Знамени инженерно-строительном институте.
Рекомендации предназначены для специалистов НИИ, КБ и заводских лабораторий, занимающихся расчетами на прочность изделий машиностроения.
4a
I. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ
Xе - местная система координат ZL‘ - базисная система координат
Ш - компоненты вектора перемещений в базисной сиотеме координат
ф - компоненты тензора деформаций в местной системе координат 6*J- компоненты тензора напряжений Si; - компоненты девиатора напряжений С( - компоненты тензора преобразования координат
- предел текучести при чистом сдвиге Т - температура
£ - параметр Одквиста Д коэффициенты Ламе
dr - коэффициент линейного теплового расвшрения Е - модуль упругости
- коэффициент Пуассона КЗ - конечный элемент
ПШ1 - пакет прикладных программ
MX - матрица жесткости
Щ - магнитный диск (том прямого доступа)
ВЗУ - внешние запоминающие устройства
АЦПУ - алфавитно-цифровое печатающее устройство.
5
2. ПОСТАНОВКА ЗАДАЧИ
2.1. Соотношения пространственной задачи термоупругости
2.1.1. Рассматривается напряженно-деформированное состояние трехмерного тела, которое занимает область $ , ограни
ченную границей Г . Физико-механические характеристики объекта изменяются произвольным образом внутри области S Тело деформируется под действием статически уравновешенной системы внешних сил и реакций связей,. Внешние воздействия могут быть представлены полем массовых внутренних сил, системой поверхностных нагрузок, приложенных на границе Г , и эквивалентными тепловыми нагрузками, вызванными неравномерным нагревом или охлаждением тела.
Важным классом пространственных задач термоупругооти являются тела вращения под действием неосесимметричного термооило-вого нагружения.
2.1.2. Для описания геометрии и граничных условий рассматриваемых объектов используется базисная система координат ZL . Внешние нагрузки и перемещение точек тела определяются проекциями в этой системе. Описание напряженно-деформированного состояния тел сложной формы упрощается в криволинейной системе координат , естественно связанной о геометрией тела. Такая система в дальнейшем называется местной.
2.1.3. Системы координат характеризуются компонентами метрических тензоров Qtj и Qtl/ , которые определяют масштабы базисных векторов и углы между ними. Символы Кристоффеля второго рода находятся по соответствующим компонентам Qtj и Qc)'
6
по формулам [ I ]
2.1,4. Полагается, что в любой точке тела известна связь между базисной и местной системами координат, осуществляемая тензором преобразования координат,
(2.2)
, if _ д21'
У “ ~ dxJ
Здесь и далее латинские буквы используются для обозначения индексов, принимающих значения 1,2,3, а греческие - 1,2.
2.1.5. Ковариантные компоненты метрического тензора в местной системе координат определяются через соответствующие компоненты в базисной
Ковариантные компоненты находятся по известным ковариент-
ным
7
(2.4)
fi ( Q'tj)
$
где - алгебраическое дополнение к элементу д-i/ мат
рицы, построенной по ковариантннм компонентам; g^d&iCgtjJ определитель этой матрицы.
+ Cl Uk'j - 2 Uк'■ Cl Cj fl'm ).
(2.5)
2.1.6. Принимается, что перемещения точек тела беоконечво малы. Тогда связь между компонентами тензора деформаций в местной системе координат и компонентами перемещений в базисной осуществляется в виде [i]
2.1.7. Для пространственных тел призматической формы в качестве базисной удобно использовать декартову систему координат В декартовых координатах не равны нулю следующие компоненты метрического тензора:
- дм - дм = f (2.6)
пк>
и вое li'm = 0. Компоненты метрического тензора в местной
системе координат определяются соотношениями
да -- Сс с]\ (2,7)
Связь между деформациями и перемещениями представляется в
виде
(2.8)
8
-9)
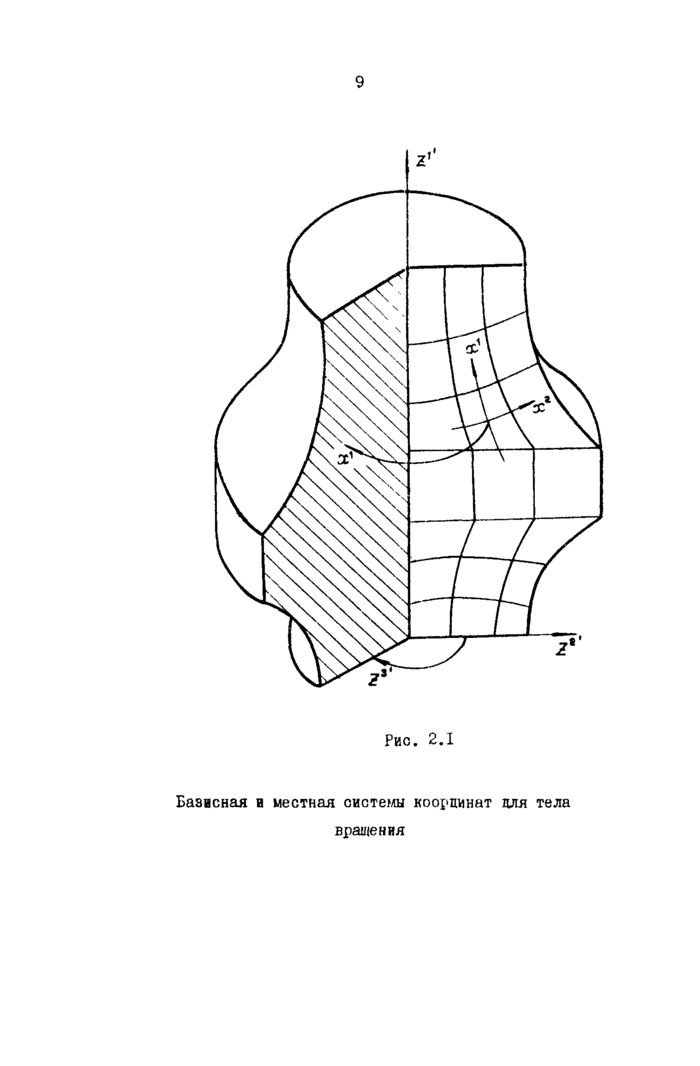
2,1.8. При исследовании тел вращения в качеотве базисной естественно принять круговую цилиндрическую систему координат (рно.2.1). В этом случае отличны от нуля; компоненты метрического тензора
9«-
символы Кристоффеля второго рода
(2.10)
пг' ryz' Н*'~ Г5‘- Х~
/5у = & ? 1з'£' " ‘2.'ъ' '%*’
Местная система координат Xе вводится таким образом, что
У 2
оси X и X расположены в плоскости меридионального сечения тела, а X6 совпадает по направлению с В9 . В силу ортогональности Хъ и В? к плоскости меридионального сечения имеем
cfi. (2ЛТ
С учетом выражений (2.9) и (2.II) компоненты метрического тензора в местной системе координат определяются соотношениями
(2.12)
Ск С ft Qrfr' •
gw
Связь между компонентами деформаций и перемещений осуществляется по формулам f ,
<4* = 7 (С<< fyfi * С/ь Щ* ) / ;
(2.13)
f - 4fи * ^)
t $ъ~ Uз'з V- Ul*
Базисная и местная системы координат для тела
вращения