ГОСТ ISO/TS 28038-2021
Статистические методы. Определение и использование полиномиальных функций при калибровке
В настоящем стандарте рассмотрены полиномиальные калибровочные функции, которые описывают связь между переменной стимула и переменной отклика. Параметры полиномиальных функций оценивают по данным калибровки, состоящим из набора пар значений стимула и отклика. Рассмотрены различные случаи, связанные с особенностями неопределенностей, связанных с данными. Оценки параметров полиномиальной калибровочной функции определяют с использованием метода наименьших квадратов с учетом заданной информации о неопределенности. Предполагается, что данные калибровки соответствуют цели и, следовательно, обработка выбросов не рассмотрена. Предполагается также, что ошибки данных калибровки подчиняются нормальному распределению. В настоящем стандарте уделено особое внимание выбору метода наименьших квадратов, соответствующего особенностям структуры неопределенности данных в каждом конкретном случае. Поскольку упоминаемые методы хорошо описаны в технической литературе, а программное обеспечение, которое их реализует, доступно, они не описаны в настоящем стандарте. Распространенные типы ковариационных матриц, связанных с данными калибровки, охватывают (а) неопределенности данных отклика, (b) неопределенности и ковариации данных отклика, (c) неопределенности данных стимула и отклика, и (d) неопределенности и ковариации данных стимула и отклика. Также рассмотрен случай, когда неопределенности данных неизвестны. Приведены методы выбора степени полиномиальной калибровочной функции в соответствии с установленными критериями. Может быть получена ковариационная матрица, связанная с оценками параметров полиномиальной функции, как один из результатов используемых методов наименьших квадратов. Для выбранной полиномиальной функции в настоящем стандарте описано использование оценок параметров и связанных с ними ковариационных матриц для прямого и обратного вычисления. Кроме того, в стандарте описано, как могут быть использованы положения Руководства ISO/IEC 98-3:2008 (GUM) для определения соответствующих стандартных неопределенностей. Рассмотрены способы учета некоторых ограничений (например, полином должен проходить через начало координат), а также использование преобразований переменных, которые могут приблизить калибровочную функцию к полиномиальной. Рассмотрена также «смена ролей» переменных. Использование настоящего стандарта иллюстрируют примеры из нескольких областей науки об измерениях
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1
стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13
стр. 14

стр. 15
стр. 16

стр. 17

стр. 18
стр. 19
стр. 20

стр. 21
стр. 22

стр. 23

стр. 24

стр. 25
стр. 26
стр. 27
стр. 28
стр. 29
стр. 30
МЕЖГОСУДАРСТВЕННЫЙ СОВЕТ ПО СТАНДАРТИЗАЦИИ, МЕТРОЛОГИИ И СЕРТИФИКАЦИИ
(МГС)
INTERSTATE COUNCIL FOR STANDARDIZATION. METROLOGY AND CERTIFICATION
(ISC)
МЕЖГОСУДАРСТВЕННЫЙ
СТАНДАРТ
ГОСТISO/TS 28038—2021Статистические методыОПРЕДЕЛЕНИЕ И ИСПОЛЬЗОВАНИЕ ПОЛИНОМИАЛЬНЫХ ФУНКЦИЙ ПРИ КАЛИБРОВКЕ
2021Статистические методыОПРЕДЕЛЕНИЕ И ИСПОЛЬЗОВАНИЕ ПОЛИНОМИАЛЬНЫХ ФУНКЦИЙ ПРИ КАЛИБРОВКЕ
ОПРЕДЕЛЕНИЕ И ИСПОЛЬЗОВАНИЕ ПОЛИНОМИАЛЬНЫХ ФУНКЦИЙ ПРИ КАЛИБРОВКЕ
(ISO/TS 28038:2018, Determination and use of polynomial calibration functions, IDT)
Издание официальное
Москва
Российский институт стандартизации 2021
Предисловие
Цели, основные принципы и общие правила проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены»
Сведения о стандарте
1 ПОДГОТОВЛЕН Закрытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ЗАО «НИЦ КД») на основе собственного перевода на русский язык англоязычной версии документа, указанного в пункте 5
2 ВНЕСЕН Межгосударственным техническим комитетом по стандартизации МТК 125 «Применение статистических методов»
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 26 августа 2021 г. Мч 142-П)
За принятие проголосовали:
|
Краткое наименование страны no МК (ИСО 3166} 004— 97 |
Код страны по МК(ИС0 3166) 004 -97 |
Сокращенное наименование национального органа по стандартизации |
|
Армения |
AM |
ЗАО «Национальный орган по стандартизации и метрологии» Республики Армения |
|
Беларусь |
BY |
Госстандарт Республики Беларусь |
|
Киргизия |
KG |
Кыргызстандарт |
|
Россия |
RU |
Россгандарт |
|
Узбекистан |
UZ |
Узстандарт |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 8 октября 2021 г. №г 1105-ст межгосударственный стандарт ГОСТ ISO/TS 28038—2021 введен в действие в качестве национального стандарта Российской Федерации с 1 января 2022 г.
5 Настоящий стандарт идентичен международному документу ISO/TS 28038:2018 «Определение и использование полиномиальных функций при калибровке» (ISO/TS 28038:2018 «Determination and use of polynomial calibration functions», IDT).
Наименование настоящего стандарта изменено относительно наименования указанного международного документа для приведения в соответствие с ГОСТ 1.5 (подраздел 3.6).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных меаду-народных стандартов соответствующие им межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДА
6 ВВЕДЕН ВПЕРВЫЕ
И
6.5 Любой конкретный набор данных калибровки (xjT yf). / = 1,..., т имеет структуру неопределенности, характерную для этих данных. В одном крайнем случае может быть ничего не известно о неопределенностях и ковариациях, и для выполнения работы необходимы предположения. В другом крайнем случае могут быть заданы все стандартные неопределенности о(х.) и и{у}) и все ковариации и(х(> х;) и и(уг. у,). На практике ситуация обычно находится между этими крайностями.
Примечание — В настоящем стандарте принято предположение, что любая не приписанная неопределенность или ковариация равна нулю.
6.6 Можно выделить следующие пять случаев, первые четыре в порядке возрастания сложности структуры неопределенности. Пятый отличается по своему характеру в том смысле, что информация о неопределенности неизвестна.
a) Неопределенности данных отклика. Приписаны стандартные неопределенности Ы.у,). i = 1.....т.
b) Неопределенности данных и ковариации отклика. Приписаны стандартные неопределенности
(см. 6.6 а)) и ковариации u(yt, у.), / = 1.....m,j = 1.....т (/ * j).
c) Неопределенности данных стимула и отклика. Приписаны стандартные неопределенности
и(у,). / = 1 т, и и(х,). /= 1.....т.
й) Неопределенности данных и ковариации стимула и отклика. Приписаны стандартные неопределенности (см. 6.6 с)) и ковариации u(x|t х.) и и(уг у;), / = 1.....m,j= 1.....т (/ * j).
е) Данные о неопределенности отсутствуют.
В случаях 6.6 а) — 6.6 d) приписанные неопределенности и ковариации суммируют как ковариационные матрицы Vx и Vy. в зависимости от ситуации, согласно 4.5.
Примечание — Случаи 6.6 а)—6.6 с) могут рассматриваться как особые случаи 6.6 d). но в вычислительном отношении они менее эффективны.
6.7 Основное различие между данными калибровки с приписанными неопределенностями и данными калибровки с неизвестными неопределенностями, сделанное в настоящем стандарте, заключается в следующем.
a) Для данных калибровки с приписанными неопределенностями и ковариациями [случаи 6.6 а)— 6.6 d)] может быть использована метрика, такая как статистика хи-квадрат (7.7.1), которая использует неопределенности и ковариации, для принятия решения о том. соответствует ли кандидат калибровочной функции, в настоящем стандарте это полином определенной степени, имеющимся данным. Этот подход предполагает, что информация о неопределенности является достоверной.
b) Для данных калибровки с неизвестными неопределенностями [случай 6.6 е)] статистика хи-квадрат все еще может быть рассчитана для рассматриваемых кандидатов полиномиальных моделей. Предполагается, что ошибки данных переменной отклика являются однородными, а ошибки данных переменной стимула — незначительными. Значение статистики хи-квадрат можно использовать для оценки стандартной неопределенности переменной отклика, а затем применяют положения пункта 6.7 а).
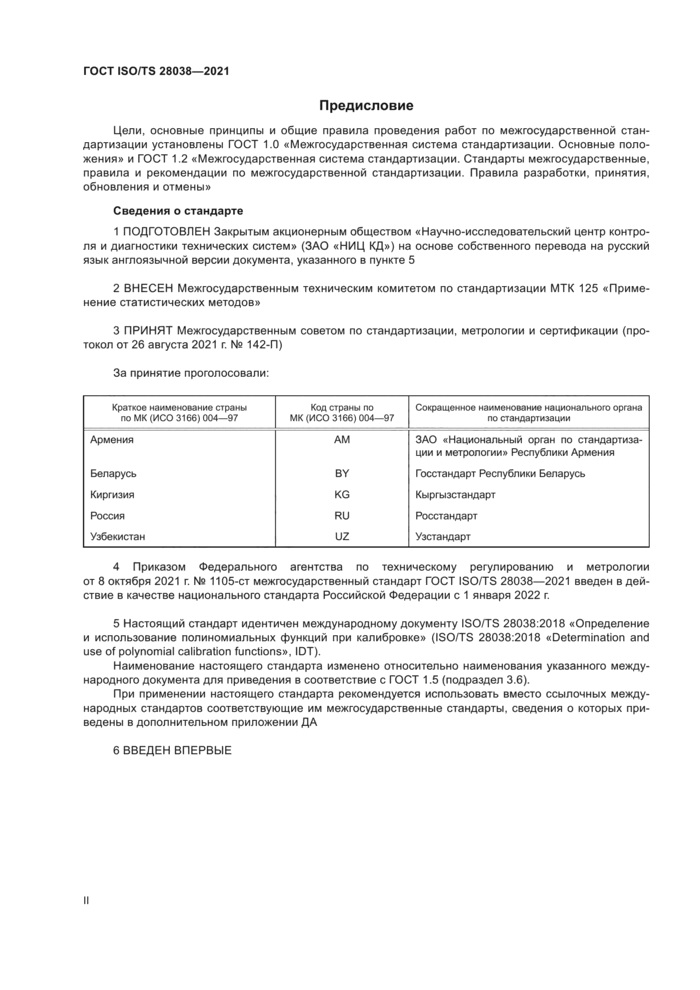
6.8 Полином выбирают из набора возможных полиномов-кандидатов различной степени в соответствии с подходящим критерием, таким как AIC (7.7.3). Для некоторых наборов данных с приписанными неопределенностями может не быть подходящего полиномиального (или любого другого гладкого) представления, согласующегося с этой информацией. Для данных на рисунке 1 а) неопределенности приписаны только значениям у. вертикальные отрезки представляют стандартную неопределенность ±1. а ковариации равны нулю. Небольшие значения стандартных неопределенностей препятствуют получению монотонной функции, согласованной с данными. Для данных на рисунке 1 Ь), идентичных данным на рисунке 1 а), за исключением того, что стандартные неопределенности примерно в три раза больше, подходит монотонный полином низкой степени. Приемлемая калибровочная функция должна быть как монотонной (7.6), так и статистически адекватной [30].
X — стимул |у.е_); Y — отклик (y.e.)
Примечание — Столбики ошибок обозначают стандартную погрешность ±1. «у.е.» обозначает единицы измерения.
Рисунок 1 — Статистическая неадекватность и адекватность калибровочной функции
Примечание — Рисунок 1а), вероятно, относится к неправильной спецификации стандартных неопределенностей, связанных с данными калибровки; их возможное исправление выходит за рамки настоящего стандарта.
6.9 Оценки параметров калибровочной функции зависят от данных калибровки и. кроме случая 6.6 е), приписанных неопределенностей и ковариаций данных. Закон распространения неопределенности (LPU) в соответствии с Руководством ISO/IEC 98-3:2008 (GUM) может быть применен для распространения неопределенностей и ковариаций данных калибровки посредством вычисления параметров калибровочной функции для получения неопределенностей и ковариаций параметров. Когда у стимула нет неопределенности (9.2,9.3 и 9.6). распространение дает точный результат, поскольку параметры полиномиальной калибровочной функции линейно зависят от значений переменной отклика и LPU в таких случаях применяется без ошибки аппроксимации (см. 7.2.1). Для других случаев (9.4 и 9.5) распространение дает приближенный результат и основано на линеаризации оценок параметров. Аппроксимация с помощью линейной функции часто соответствует целям практических задач калибровки.
Примечание — Если линеаризация для этой цели не подходит, например, когда неопределенности значений стимула велики, распространение распределений может быть использовано для определения оценок параметров. неопределенностей и ковариаций. Такой подход (Руководство ISO/IEC 98-3:2008/Дол.2:2011), в котором применяют метод Монте-Карло, не рассмотрен в настоящем стандарте.
6.10 Информация о неопределенности, относящаяся к параметрам калибровочной функции, принимает форму ковариационной матрицы для оценок этих параметров. Эта информация может быть представлена как в виде стандартных неопределенностей, связанных с этими параметрами, так и их корреляционной матрицы (определение 3.4), которая может быть более полезной. Любая форма может быть использована для вычисления стандартной неопределенности в обратных или прямых вычислениях.
6.11 Если калибровочную функцию используют для обратных вычислений (12.2), применение LPU дает приближенный результат, даже для полиномов первой степени, поскольку при обратном вычислении полином является нелинейным по своим параметрам. При этом приближение, связанное с линеаризацией, часто соответствует цели.
Примечание — Если можно выразить полиномиальную калибровочную функцию как функцию х or у, то определенную полиномиальную калибровочную функцию используют непосредственно, и на этой стадии вычислений нет ошибок линеаризации.
7 Применение полинома в качестве калибровочной функции
7.1 Общие положения
7.1.1 Для данных калибровки в настоящем разделе рассмотрено определение соотношения у = р„(х). описывающего зависимую переменную у как полиномиальную функцию степени п от независимой переменной х.
7.1.2 Если степень п заранее не известна, что часто бывает, она должна быть определена. В 7.7 показано определение степени, для которой результирующая функция удовлетворяет критериям пригодности.
7.1.3 Информация, используемая для определения полиномиальной калибровочной функции, представляет собой данные калибровки и все неопределенности и ковариации данных калибровки.
В настоящем стандарте данные калибровки обозначены (хг у,), i = 1.....т, то есть т пар измеренных
значений х и у. Также должна быть установлена наивысшая степень птак полинома, где птах меньше числа различных значений х..
Примечание — В приложении D ISO/TS 28037:2010 указано, как неопределенности и ковариации, связанные с измеренными значениями отклика и стимула переменных, могут быть получены в некоторых случаях с интерпретацией этой информации.
7.2 Работа с полиномами
7.2.1 Полином со степенью выше единицы является нелинейным по переменной х. но линейным
по своим параметрам (коэффициентам). Полином степени п (порядок п+1) имеет л+1 коэффициент. Его можно записать в мономиальной форме с коэффициентами h0.....h„:
PnW • + М + М2 +••■+Лпх" - J hy. (4)
г-о
7.2.2 Функции 1,х,х2.....хР известны как мономиальные базисные функции для полиномов степени
п. Полином степени 1 — прямая линия, степени 2 — квадратичная функция, степени 3 — кубическая функция и т. д. Причиной обращения к полиномам является то. что для их определения требуется только п сложений и п умножений (7.4).
7.2.3 Полиномы часто подходят для представления гладкой кривой или данных, генерированных на основе гладкой кривой на заданном интервале. Полиномы чрезвычайно гибки: математически полином соответствующей степени может аппроксимировать любую гладкую (непрерывную) кривую с заданной точностью. Полиномы невысокой степени менее подходят для представления кривых с резкими изменениями значений или градиента или для описания эффекта насыщения.
7.2.4 Несмотря на то. что описание полиномиальных функций в мономиальной форме [формула (4)) проясняет их природу, использование этой формы может привести к трудностям при расчетах и интерпретации вклада отдельных членов. Первая трудность заключается в том. что при |х| » 1 члены Xе становятся очень большими с увеличением г. Аналогично, для |х| « 1 члены Xе становятся очень малыми с увеличением г. Этот дисбаланс может быть устранен за счет работы с полиномами с нормализованной переменной t, принимающей значения в интервале (-1.1), которая линейно зависит от х. таким образом гарантируя, что (преобразованный) полином также имеет степень п по переменной t. Если х принадлежит интервалу [х^,,. хтах}, то
f - ~ ~ ,g,
*max ~
со всеми степенями принадлежит интервалу [-1.1]. Полином может быть преобразован к виду
л
Ро(0 - 90 + Q,/ > 92^ + - Я/ (6)
г-0
с некоторыми коэффициентами qQ.....q Вторая трудность связана с тем. что. особенно при больших
Л мономиальная базисная функция fвыглядит аналогично f в интервале [-1.1]. На рисунке 2 а)
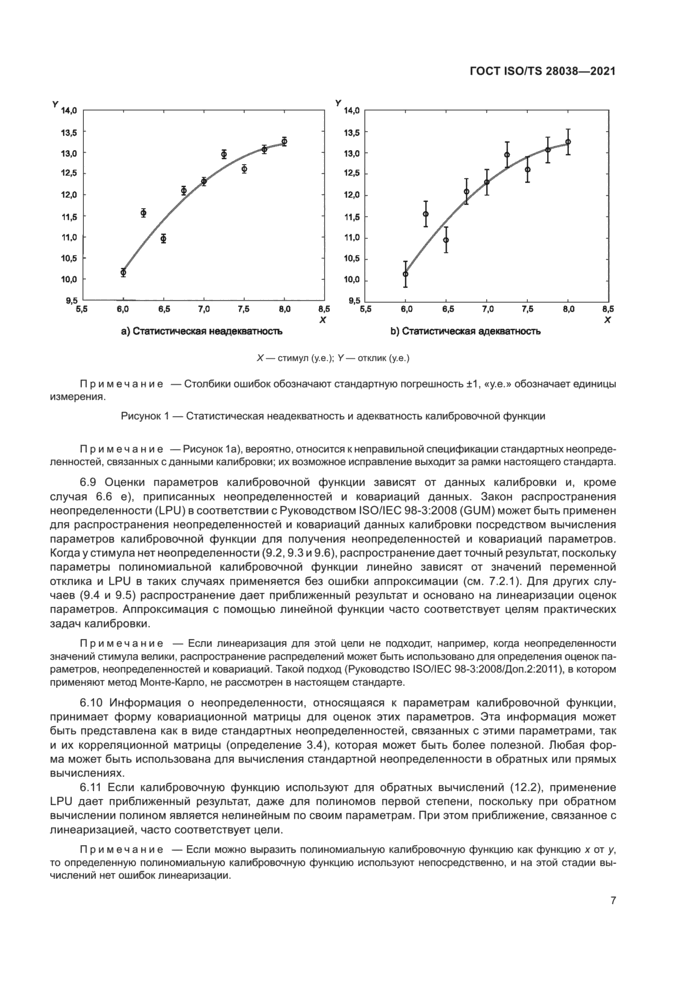
изображены мономиальные функции t2 (верхняя кривая), f*. I6 и f8 (нижняя кривая). Сходство этих базисных функций приводит к плохой обусловленности при определении мономиальных параметров, что означает потерю точности. Эта ситуация быстро ухудшается с увеличением степени, в результате чего потеря точности может стать катастрофической для более высоких степеней полинома. Третья трудность связана с интерпретацией коэффициентов в мономиальной форме калибровочной функции при переходе к исходной переменной, а именно в формуле (4). Тем не менее, в формуле (6). мономиальной форме с преобразованной переменной t, член с f вносит вклад со значением от -| qr | до | qr |. причем по крайней мере одно из этих значений достигается в конечных точках интервала [-1.1].
■>Циоишмы!фушщиft ft Я и ft b] Полиномы Чебышеве 7*(0. Г4(0и Tf(fl
не интервале f-1,1]
X — независимая переменная I. Y — зависимая переменная
Рисунок 2 — Мономиальные функции и полиномы Чебышева
7.2.5 Существуют другие формы базисных функций, которые имеют даже лучшие свойства, чем формула (6). Полиномы Чебышева TJH), используемые в настоящем стандарте, являются одним из таких наборов базисных функций. Они определены повторением на интервале [-1,1] (см. [6], с. 1):
т -1. т - /. тг<о - 2ггг_,(о - тг_г( о, г а 2. (?)
Полиномы Чебышева также могут быть определены с помощью тригонометрических соотношений:
Tf(cos0) -cosrt), cos = (8)
Рп(х) = Рп(0 ** 30T0(t)+,..^anTn(t) - J aJM
О)
г-О
На рисунке 2 б) изображена T2(t) (с наименьшей периодичностью), 73(f). T4[t) и Ts(t) (с наибольшей периодичностью). В целом можно показать, что набор 7Д/) приводит к гораздо лучшим результатам, чем V. Чебышевское представление полинома степени п:
Примечание — Другой класс базисных функций, предложенный Форсайтом [16], описан в [7]. где приведен алгоритм для преобразования формы Форсайта в представление Чебышева. Форма Форсайта основана на генерации набора базисных функций, которые ортогональны относительно значений х. Хотя форма Форсайта обладает превосходными числовыми свойствами, базисные функции Форсайта зависят от значений х. что делает их использование в сочетании с полиномами из других источников неудобным. Кроме того, форма Форсайта не была обобщена на данные, имеющие неопределенности значений х или какие-либо ковариации.
7.3 Выбор интервала определения калибровочной функции в обратной задаче
7.3.1 Рассмотрим использование калибровочной функции рп{х) для обратного вычисления (12.2). то есть для определения значения х0 переменной стимула х, соответствующего значению у0 переменной отклика у. особенно в случае, когда х0 находится вблизи конца интервала (xmin, хтах]. на котором определена функция р„(х). Предположим, что рп(х) строго возрастает на интервале [xmin, xmax] (аналогично в случае убывания). Значения у в конечных точках интервала: ymin = P„(xmin) и ymax = p„(*max)- Для любого значения у0 из интервала [ym>n. ymaJ х0 однозначно определяется путем решения уравнения р„(х0) = у0. Однако, поскольку у0 обладает неопределенностью, это значение может находиться за пределами интервала [ymin, ymax], в результате чего Xq тоже находится за пределами интервала [xmjn, хтах].
Примечание — При прямом вычислении таких проблем нет.
7.3.2 Существует два способа действий в такой ситуации. Первый — рассматривать значения у0 только в интервале [ymin, ymax], что ограничивает применение калибровочной функции. Второй способ — увеличить интервал, на котором определена калибровочная функция. Одна из возможностей состоит в том. чтобы как можно меньше расширить интервал [min, х„ max, х,], например, до [min, х, - Дх. max, х- ♦ Дх]. где Дх = 0.1 (max, х. - min, х.). Подходящий интервал в каждом конкретном случае определяют экспериментальным путем. При выборе подходящего интервала могут быть использованы существующие обоснования (при наличии). Наиболее экстремальный случай возникает, когда градиент калибровочной кривой мал по величине, поскольку небольшое изменение отклика вызывает большое изменение стимула [см. калибровочную функцию оптической плотности пленки на рисунке 5 Ь) для значений отклика в окрестности 0,45]. В настоящем стандарте для примеров выбраны подходящие интервалы [xmin, хгаах].
7.3.3 Интервал [min, х,. max, xj должен быть увеличен в наименьшей степени для уменьшения экстраполяции за пределы диапазона данных, что обычно считается небезопасным.
Примечание — В примере с оптической плотностью пленки (см. 7.5.3 и 9.2) использование Дх = 0.1 (max, х, - min^ х^) не подходит при обратной интерполяции для у0. близких к Утах. как определено в 7.3.1 с и(у0) = 0,003. но замена 0.1 на 0.15 оказывается удовлетворительной.
7.4 Использование представления Чебышева
7.4.1 Используя полиномы Чебышева и нормализованную переменную (5). можно применять численно устойчивые полиномиальные функции со степенями от средних до высоких [2]. Дополнительные преимущества и свойства описаны в 7.4.2—7.4.4 и проиллюстрированы в настоящем стандарте.
7.4.2 Представление полинома с помощью полиномов Чебышева (9) р„(х,а) со степенью п (п > 0)
сводится к определению параметров (коэффициентов) а = (э0.....ал)т и границ xmin и хтах интервала
определения функции. При определении рп для всех значений х в интервале [xmm, xmax] рекомендуется использовать алгоритм Кленшоу [5]. как показано в таблице 1. Для сравнения в таблице 1 так же приведена схема расчетов Хорнера [19] для мономиальной формы pn = hQ + />,х + ... + /)„хл (см. 7.2.1). Форма Чебышева может быть оценена с применением 2п сложений (или вычитаний) и п умножений по сравнению с с сложениями и п умножениями в случае мономиальной формы.
|
Таблица 1 — Определение полинома с применением полиномов Чебышева и мономиальной формы | |||||||||||||||
|
7.4.3 Для многих полиномиальных калибровочных функций степень полинома обычно не высока, это 1. 2. 3 или 4. Для таких случаев использование мономиального представления (6) с нормализованной (не исходной) переменной, как правило, является не сложной в вычислительном отношении задачей. Тем не менее, рекомендуется при построении полиномиальной калибровочной функции применять представление Чебышева, особенно если величина калибровочной функции в конечной точке х интервала, на котором применяют калибровочную функцию, очень велика или очень мала по сравнению с единицей.
7.4.4 Существуют случаи, такие как Международная температурная шкала ITS-90 [13]. когда используют опорные функции с относительно высокими степенями, такими как 12 или 15. Для таких функций работа с нормализованной переменной, как в (5) обеспечивает существенные вычислительные преимущества, а форма Чебышева обеспечивает не только вычислительные преимущества, но также преимущества в управляемости, а иногда и более компактном представлении. Некоторые из этих преимуществ представлены в примере.
Пример — Термоэлектрическое напряжение (на основе [9]).
Мономиальное представление термоэлектрического напряжения
е-2с'г
г-0
в опорной функции для термопар типа S и температуры по Цельсию Т в интервале [-50 °С, 1064,18 °С] приведено в базе данных NIST [1]. Отношения ненулевых коэффициентов наибольшего и наименьшего составляет 1021, коэффициенты вычисляют до 12 значащих десятичных цифр (12S); (предполагалось, что необходима высокая точность). В таблице 2 (столбец «Исходное значение с,») значение сг приведено с пятью значащими цифрами.
|
Таблица 2 — Полиномиальные коэффициенты для термопары типа S | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Переменная масштаба Т = 77В использована в работе ITS-90 в последние годы, где в этом случае
п
В = 1064.18 °С и выходит за правую границу интервала. Затем если Сг » В'С,, Е - ^ C,fr. Масштаб
г-0
предполагает, что вклад r-го слагаемого в сумму ограничен величиной |Сг|. Значения Е в мВ обычно
необходимо определять с тремя знаками после запятой. Соответственно, коэффициенты сг
приведены в таблице 2 (столбец «Масштабированное значение, Сг») с четырьмя знаками после запятой, что облегчает проверку. Альтернативно, переменная может быть приведена к интервалу [-1.1] (в ITS-90 не сделано) с использованием формулы (5) для х=Т. xmn=-50 "С и хтах=В. Соответствующие коэффициенты приведены в столбце «Нормализованное значение», а коэффициенты Чебышева в столбце «Форма Чебышева» с четырьмя знаками после запятой. Коэффициенты получены с использованием [7] и [31].
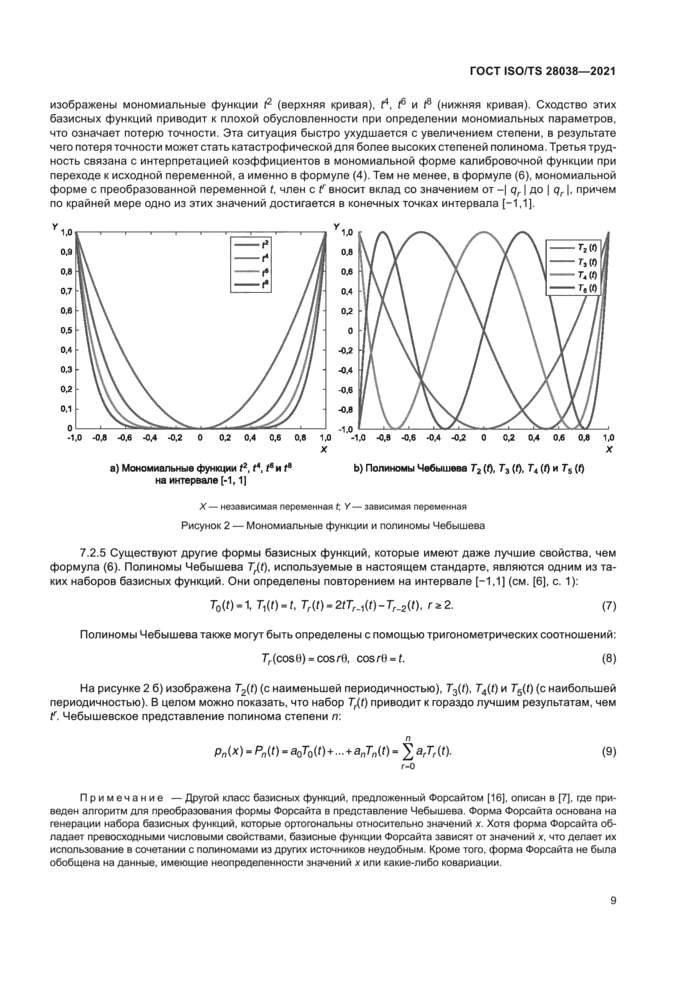
На рисунке 3 изображена опорная функция. Она изгибается очень плавно, но присутствующую нелинейность нельзя игнорировать. Коэффициенты мономиального представления для исходной или масштабированной переменной в таблице 2 не указывают на слегка изогнутую форму. Однако нормализованная форма и форма Чебышева (см. таблицу 2), поскольку первые два коэффициента являются доминирующими, указывают на то. что калибровочная функция имеет заметную линейную (прямолинейную) составляющую. Коэффициенты Чебышева для степеней 8 и, возможно, 7 могут быть заменены на ноль, что приводит к получению полинома с более низкой степенью, поскольку в расчеты они вносят небольшой вклад или вообще не вносят вклада. Такие рассуждения не могут быть непосредственно применены к другим полиномиальным представлениям.
|
X — температура. Т (*С); У — термоэлектрическое напряжение. Е (мВ) Рисунок 3 — Соотношение между температурой и термоэлектрическим напряжением |
7.5 Оценка пригодности полиномиальной функции: визуальный контроль
7.5.1 Как и во многих задачах, связанных с анализом данных, важен визуальный контроль функции-кандидатов. Это особенно полезно в задачах калибровки, где доступно ограниченное количество данных. В таких случаях одни только статистические критерии, используемые для оценки функции-кандидатов. часто не обладают достаточной статистической мощностью.
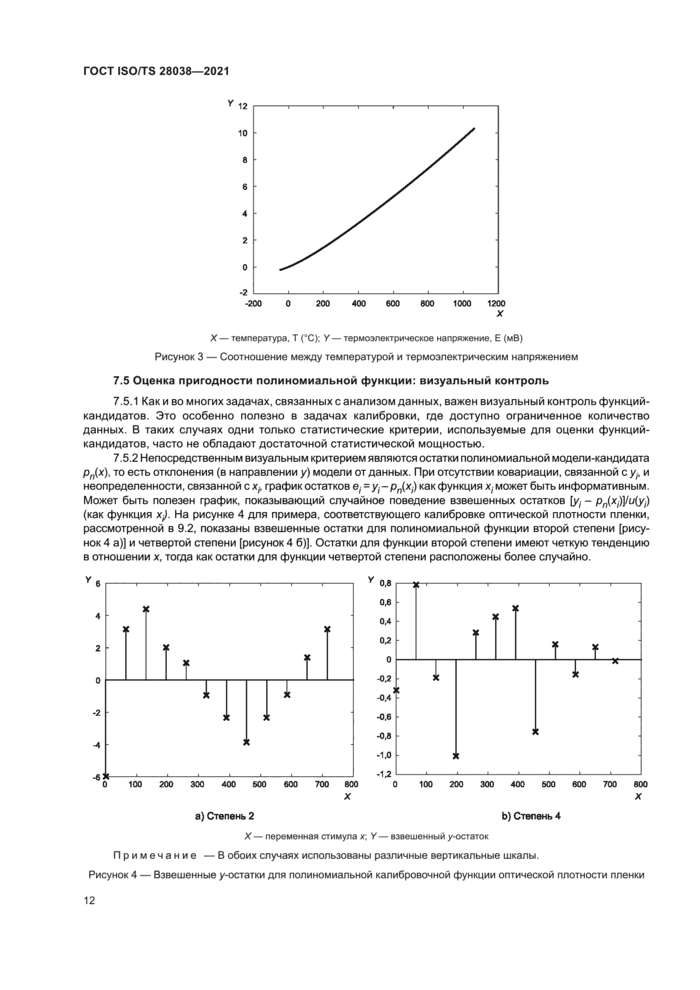
7.5.2 Непосредственным визуальным критерием являются остатки полиномиальной модели-кандидата рп(х). то есть отклонения (в направлении у) модели от данных. При отсутствии ковариации, связанной с у(> и неопределенности, связанной с х,. график остатков е,=у<-рл(х,) как функция х, может быть информативным. Может быть полезен график, показывающий случайное поведение взвешенных остатков [у( - р„(х))/и(у|) (как функция х). На рисунке 4 для примера, соответствующего калибровке оптической плотности пленки, рассмотренной в 9.2, показаны взвешенные остатки для полиномиальной функции второй степени [рисунок 4 а)] и четвертой степени [рисунок 4 б)]. Остатки для функции второй степени имеют четкую тенденцию в отношении х. тогда как остатки для функции четвертой степени расположены более случайно.
|
а)Отчппь2 Ь) Степень 4 X - переменная стимула х; V - взвешенный у-остаток Примечание — В обоих случаях использованы различные вертикальные шкалы. Рисунок 4 — Взвешенные у-остатки для полиномиальной калибровочной функции оптической плотности пленки |
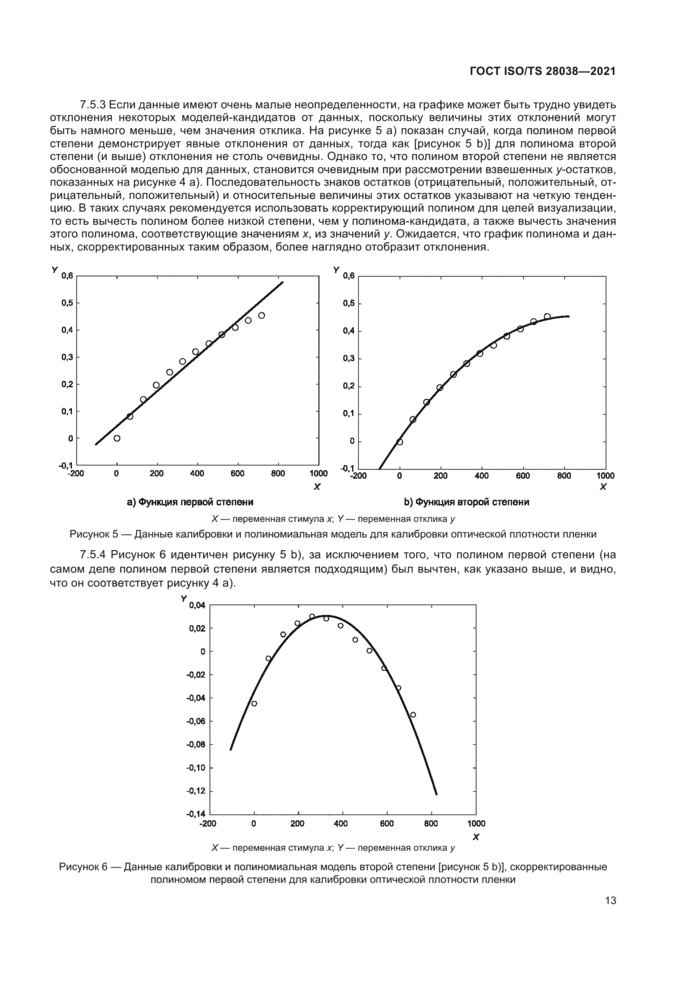
7.5.3 Если данные имеют очень малые неопределенности, на графике может быть трудно увидеть отклонения некоторых моделей-кандидатов от данных, поскольку величины этих отклонений могут быть намного меньше, чем значения отклика. На рисунке 5 а) показан случай, когда полином первой степени демонстрирует явные отклонения от данных, тогда как [рисунок 5 Ь)] для полинома второй степени {и выше) отклонения не столь очевидны. Однако то. что полином второй степени не является обоснованной моделью для данных, становится очевидным при рассмотрении взвешенных у-остатков. показанных на рисунке 4 а). Последовательность знаков остатков (отрицательный, положительный, отрицательный. положительный) и относительные величины этих остатков указывают на четкую тенденцию. В таких случаях рекомендуется использовать корректирующий полином для целей визуализации, то есть вычесть полином более низкой степени, чем у полинома-кандидата, а также вычесть значения этого полинома, соответствующие значениям х, из значений у. Ожидается, что график полинома и данных. скорректированных таким образом, более наглядно отобразит отклонения.
|
X — переменная стимула х\ У — переменная отклика у Рисунок 5 — Данные калибровки и полиномиальная модель для калибровки оптической плотности пленки |
7.5.4 Рисунок 6 идентичен рисунку 5 Ь). за исключением того, что полином первой степени (на самом деле полином первой степени является подходящим) был вычтен, как указано выше, и видно, что он соответствует рисунку 4 а).
|
X — переменная стимула х\ У — переменная отклика у Рисунок 6 — Данные калибровки и полиномиальная модель второй степени [рисунок 5 Ь)]. скорректированные полиномом первой степени для калибровки оптической плотности пленки |
7.5.5 При наличии ковариаций, связанных с у., график трансформированных взвешенных отклонений Ly-'e по х может быть информативным. Точно так же. если есть ковариации, связанные с х.. может быть полезен график трансформированных взвешенных отклонений L/'d по у. Здесь Ly^Lx —
нижние треугольные матрицы, заданные факторизациями Холецкого [18]. V = LLJ и V = L /J
у у у х ж *
Примечание — Нормирование с помощью стандартных неопределенностей 0(6,). связанных с в;, также может быть полезно.
7.6 Оценка пригодности полиномиальной функции: монотонность
7.6.1 Калибровочную функцию часто используют для определения значения стимула по заданному значению отклика или наоборот. В качестве альтернативы, функция, которая должна быть использована для этой цели, может состоять из суммы «опорной» функции и калибровочной функции, например, при использовании Международной температурной шкалы ITS-90 [13] (см. также пример в 7.4.4). В последнем случае любой критерий проверки монотонности может быть применен к составной функции.
7.6.2 Для использования в качестве калибровочной функции, функция, как правило, должна быть строго монотонной, то есть функция должна строго возрастать или убывать на интервале определения. Это условие необходимо, чтобы гарантировать, что для любого возможного значения отклика существует единственное значение стимула. Простой способ проверки монотонности состоит в том, чтобы оценить калибровочную функцию в точном интервале х (1000 равномерно расположенных точек, скажем, через одинаковый интервал значений стимула), чтобы увидеть, показывают ли эти значения увеличение или уменьшение. Для случая, когда калибровочная функция является полиномом, в приложении А приведен более строгий способ проверки монотонности.
Примечание —В особых случаях может быть подходящей немонотонная калибровочная функция. В такой ситуации необходимо установить правило выбора подходящего значения переменной стимула, соответствующего значению переменной отклика и сопроводительной информации.
7.7 Оценка пригодности полиномиальной функции: степень
7.7.1 Степень л полиномиальной калибровочной функции часто априори неизвестна. Она может быть выбрана путем анализа полиномиальных функций по возрастанию степеней, формирования меры критерия согласия для каждой функции и выбора на основе этих мер подходящей степени полинома. Обычной мерой, когда неопределенности связаны только с yt [случай 6.6 а)], является статистика хи-квадрат Хоьв — сумма квадратов отклонений полинома степени л от у(, взвешенная обратно пропорционально
квадратам стандартных неопределенностей, связанных со значениями у, (см. 9.2). Если присутствуют ковариации, связанные с yt [см. 9.3. случай 6.6 Ь)]. используют модифицированную меру:
(Ю)
где 6( = у, - рл(х/. а) — отклонения от полинома степени л. соответствующие оценке а параметра а. Если имеются также неопределенности и. возможно, ковариации, связанные с х, [случаи 6.6 с) и 6.6 d)], используют дополнительную меру, которая учитывает эти знания (см. 9.4 и 9.5). Иногда используют 2
обозначение Хоь*(л), когда необходимо указать явную зависимость от степени л.
7.7.2 В настоящем стандарте предполагается, что информация о неопределенности представлена вместе с данными, и. соответственно, единственными оцениваемыми параметрами являются л-И полиномиальный коэффициент. В исключительных случаях, когда информация о неопределенности недоступна, делают соответствующие предположения (см. 9.6). В этом случае также оценивают стандартное отклонение ошибок в значениях у.
7.7.3 В случае, когда информация о неопределенности доступна, в настоящем стандарте использованы общепринятые критерии выбора модели, в частности, информационный критерий Акаике (AIC), скорректированный AIC (А1Сс) и байесовский информационный критерий (BIC) [4]. которые применяют, когда можно предполагать, что ошибки данных калибровки подчиняются нормальному распределению, как предполагается в разделе 9. Для т точек данных и полиномиальной модели с л+1 параметрами эти критерии имеют вид:
АЮМ-ХвиДО+Ял+и.
А1Сс(л) ■ АЮ(п) + 2-^, (11)
т-п-2 '
В1С(л) = х^Ьв(л) + (п + 1)1пт.
7.7.4 Все три критерия предназначены для того, чтобы сбалансировать правильность выбора и простоту модели. Учитывая число моделей-кандидатов. а именно полиномов со степенями п = 1, .... лтах, для подходящего выбора максимальной степени птах. обычно выбирают модель, имеющую наименьшее значение AIC (или А1Сс или BIC). Некоторые эксперименты [34] с этими критериями для полиномиального моделирования показали, что выполнение AIC и BIC аналогично, хотя А1Сс больше подходит для небольших наборов данных. Несмотря на то. что для получения убедительных выводов требуется больше опыта, для практических задач полиномиальной калибровки есть некоторые свидетельства того, что обычно одна и та же степень полинома выбирается по трем критериям, когда все они могут быть использованы. Это касается примеров, приведенных в настоящем стандарте. Тем не менее, поскольку вычисления, связанные с определением значений для всех трех критериев, минимальны, все они могут быть проверены.
Примечание 1 — Значения AIC для различных значений п можно сравнивать между собой, как и значения А!Сс или BIC. Например, значения AIC нельзя сравнить со значениями BIC.
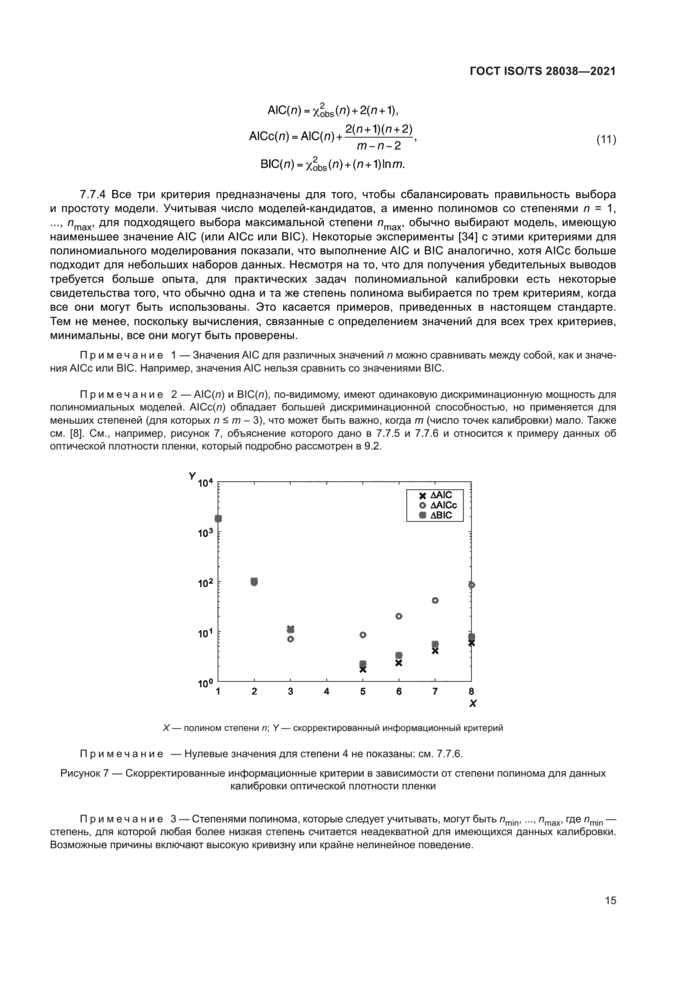
Примечание 2 — А1С(п) и В1С(л). по-видимому, имеют одинаковую дискриминационную мощность для полиномиальных моделей. А1Сс{п) обладает большей дискриминационной способностью, но применяется для меньших степеней (для которых п й т-3), что может быть важно, когда т (число точек калибровки) мало. Также см. [8]. См., например, рисунок 7. объяснение которого дано в 7.7.5 и 7.7.6 и относится к примеру данных об оптической плотности пленки, который подробно рассмотрен в 9.2.
X AAJC ОДАЮо ■ ЛЯЮ
10я
101
*
о
4
!1
7
в
х
X — полином степени п; У -- скорее».тированный информационный критерий
Примечание — Нулевые значения для степени 4 не показаны: см. 7.7.6.
Рисунок 7 — Скорректированные информационные критерии в зависимости от степени полинома для данных
калибровки оптической плотности пленки
Примечание 3 — Степенями полинома, которые следует учитывать, могут быть .....лпвх, где л,„п —
степень, для которой любая более низкая степень считается неадекватной для имеющихся данных калибровки. Возможные причины включают высокую кривизну или крайне нелинейное поведение.
Информация о введении в действие (прекращении действия) настоящего стандарта и uat/e-нений к нему на территории указанных выше государств публикуется в указателях национальных (государственных) стандартов, издаваемых в этих государствах, а также в сети Интернет на сайтах соответствующих национальных органов по стандартизации.
В случав пересмотра, изменения или отмены настоящего стандарта соответствующая информация будет опубликована в сети Интернет на сайте Межгосударственного совета по стандартизации. метрологии и сертификации в каталоге «Межгосударственные стандарты»
©ISO. 2018 © Оформление. ФГБУ «РСТ», 2021
В Российской Федерации настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
7.7.5 На практике вместо этого может быть использован скорректированный критерий ДА1С(л) = = А1С(л) = AICmin, где AICmjn — минимум А1С(1), ..., А1С(лтах). Критерии А1Сс и BIC могут быть скорректированы аналогичным образом. Поскольку для заданного набора данных А1Сга|П является константой, скорректированный критерий является просто сдвигом исходного критерия, и поэтому скорректированные значения можно сравнивать так же, как и исходные значения. Пусть п = л* при минимальном значении AIC. Тогда п = /?* является оптимальной степенью по критерию и ДА1С(л*) = 0.
7.7.6 График значений ДА1С(1).....ДА1С(/»так) относительно п вместо или в дополнение к таблице
их значений, может быть информативным. Если значения ДА1С(1).....ДА1С{лтах) (за исключением
ДА1С(л*) равного нулю], охватывают несколько порядков, полезно построить значения в зависимости от л в логарифмическом масштабе. В таком случае нуль ДА1С(л*) находится «вне графика», так как его логарифм равен -•». См. рисунок 7 в качестве примера.
V2
Л7-Л-1
RMSR(n)-
(12)
7.7.7 Со статистикой Хоь* связан корень среднеквадратичного остатка (RMSR), который применяют для л </л-1;
При увеличении л значения RMSR(n) имеют тенденцию сначала уменьшаться, а затем стабилизироваться, когда набор данных калибровки подходит для представления с помощью полинома.
Примечание 1 — Значения RMSR часто уменьшаются еще раз для бопее высоких степеней, если полиномиальная функция более точно отражает помехи в данных (см. также [7]).
Примечание 2 — R2 — статистический показатель, часто используемый на практике, отражающий «долю дисперсии относительно среднего у-данных. объясненную с помощью выбранной функции» [33]. Эта мера и некоторые ее обобщения применяют только к простейшим структурам неопределенности, таким как 6.6 а) и 6.6 е), и поэтому она не подходит для общих целей калибровки.
7.7.8 Значения AIC, AICc. BIC и RMSR для л = 1.....лтах можно использовать для первоначального
выбора степени полинома. Хотя RMSR традиционно используют для выбора подходящей степени полинома [7], может быть трудно решить, для какой степени RMSR должны быть стабилизированы для практических целей, особенно в случае небольших наборов данных, часто используемых при калибровке.
Поэтому, по-возможности, рекомендуется использовать для этой цели один из информационных критериев, который, как правило, дает более четкое решение. Полином, выбранный таким образом, всегда следует дополнительно оценивать на пригодность, используя визуальную проверку (см. 7.5), проверку монотонности (см. 7.6), если это возможно, или. что важно, используя знания о предполагаемом применении.
7.8 Проверка адекватности (валидация) калибровочной функции
7.8.1 Рассмотрим полиномиальную функцию степени л, выбранную в соответствии с 7.7. В предположении, что данные калибровки представляют собой реализации случайных величин, подчиняющихся нормальному распределению (не обязательно независимых), величина, для которой формула (10) является реализацией, подчиняется распределению х* с v = т - п - 1 степенями
свободы. Соответственно, вероятность того, что Xots превышает конкретный квантиль х*. может быть определена. Рекомендуется использовать квантиль уровня 95 %.
2
7.8.2 Если Xobs для степени полинома, указанной одним или несколькими информационными критериями, превышает квантиль уровня 95 %. считается, что полиномиальная калибровочная функция не может рассматриваться для описания данных. Более того, такой результат означает, что соответствующие оценки параметров ё и соответствующую ковариационную матрицу V6 следует рассматривать как недостоверные, также как и все значения и неопределенности, полученные на основе функции (см. 7.9). В таком случае данные и связанные с ними неопределенности следует пересмотреть. В качестве альтернативы и. возможно, дополнительно, могут быть рассмотрены полиномы, имеющие степени, близкие к выбранным с использованием 7.7. Может быть использована калибровочная
Содержание
1 Область применения..................................................................1
2 Нормативные ссылки..................................................................1
3 Термины и определения................................................................2
4 Обозначения............................... 3
5 Стандарты, использующие полиномиальную калибровочную функцию.........................5
6 Данные калибровки и связанные с ними неопределенности..................................5
7 Применение полинома в качестве калибровочной функции..................................8
8 Общий подход к определению полиномиальной калибровочной функции......................17
9 Статистические модели структур неопределенности.......................................18
10 Полиномы, удовлетворяющие заданным условиям.......................................33
11 Преобразование и «смена ролей» переменных...........................................33
12 Использование полиномиальной калибровочной функции..................................35
Приложение А (справочное) Проверка монотонности полинома................................37
Приложение В (справочное) Стандартная неопределенность в обратном вычислении ............38
Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов
межгосударственным стандартам .........................................39
Библиография........................................................................40
Введение
0.1 Калибровка является центральным исследованием при выполнении измерений и включает в себя подбор в соответствии с результатами измерений функции, описывающей взаимосвязь переменной отклика (зависимой переменной) у с переменной стимула (независимой переменной) х. Далее эту функцию используют при калибровке. В настоящем стандарте рассмотрены полиномиальные калибровочные функции, которые зависят от набора параметров (коэффициентов). Целью калибровки является следующее:
a) оценка параметров калибровочной функции с учетом данных калибровки, полученных с помощью измерительной системы, и оценка ковариационной матрицы, связанной с оценками параметров. Все неопределенности, связанные сданными, следует учитывать;
b) использование полученной калибровочной функции для обратного вычисления, то есть для определения значения стимула, соответствующего дополнительно измеренному значению отклика, а также для определения стандартной неопределенности, соответствующей значению стимула с учетом стандартной неопределенности, соответствующей значению отклика. Калибровочную функцию иногда используют для прямого вычисления, то есть для определения значения отклика, соответствующего дополнительно измеренному значению стимула, а также для вычисления стандартной неопределенности. соответствующей значению отклика с учетом стандартной неопределенности, соответствующей значению стимула.
В настоящем стандарте приведены способы выполнения этих вычислений с использованием признанных алгоритмов. В стандарте приведены примеры по калибровке: пленки по интенсивности оптического поглощения (NPL), расходомера (INRIM). термометра сопротивления (DFM). при анализе природного газа (VSL) и количественном определении содержания по изотопам (NRC).
0.2 Особенности информации о неопределенности данных калибровки влияют на способ оценки параметров калибровочной функции и представления связанной ковариационной матрицы. Эта информация о неопределенности может включать количественные эффекты ковариации измерений, относящиеся к зависимостям между задействованными величинами.
0.3 Поскольку в любом конкретном случае степень полиномиальной калибровочной функции обычно не известна, в настоящем стандарте рекомендуется определять полиномиальные функции всех степеней вплоть до оговоренной (ограниченной количеством доступных данных) с последующим выбором одной из этих степеней в соответствии с подходящими критериями. Один критерий связан с требованием монотонности калибровочной функции (строгого возрастания или убывания) в области определения. Второй критерий относится к обеспечению баланса между полиномиальной калибровочной функцией, позволяющей удовлетворительно описывать данные, и количеством параметров полинома. Еще один критерий относится к визуальному принятию полиномиальной функции.
0.4 Таким образом, определение и использование полиномиальной калибровочной функции состоит из следующих этапов:
1) получения данных калибровки и доступной информации об их неопределенности, включая информацию о ковариации, если она доступна;
2) определения полиномиальных функций всех степеней вплоть до заданного максимума способом. учитывающим информацию о неопределенности:
3) выбора подходящей функции из этого набора полиномиальных функций в соответствии с критериями, указанными в 0.3:
4) определения оценок параметров выбранной полиномиальной функции и связанной ковариационной матрицы;
5) использования калибровочной функции для обратного вычисления и определения соответствующей неопределенности:
6) использования калибровочной функции для прямого вычисления и определения соответствующей неопределенности.
0.5 В настоящем стандарте рассмотрены этапы 2—6. перечисленные в 0.4. с использованием принципов Руководства ISO/1EC 98-3:2008 (GUM). Поэтому, как часть этапа 1. перед применением настоящего стандарта пользователь должен иметь доступные стандартные неопределенности и ковариации. связанные с измеренными значениями х и у.
При определении этих неопределенностей следует учитывать положения GUM на основе модели измерения, установленной для рассматриваемой области.
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
Статистические методы ОПРЕДЕЛЕНИЕ И ИСПОЛЬЗОВАНИЕ ПОЛИНОМИАЛЬНЫХ ФУНКЦИЙ ПРИ КАЛИБРОВКЕ
Statistical methods. Determination and use of polynomial calibration functions
Дата введения — 2022—01—01
1 Область применения
1.1 В настоящем стандарте рассмотрены полиномиальные калибровочные функции, которые описывают связь между переменной стимула и переменной отклика. Параметры полиномиальных функций оценивают поданным калибровки, состоящим из набора пар значений стимула и отклика. Рассмотрены различные случаи, связанные с особенностями неопределенностей, связанных с данными.
1.2 Оценки параметров полиномиальной калибровочной функции определяют с использованием метода наименьших квадратов с учетом заданной информации о неопределенности. Предполагается, что данные калибровки соответствуют цели и. следовательно, обработка выбросов не рассмотрена. Предполагается также, что ошибки данных калибровки подчиняются нормальному распределению. В настоящем стандарте уделено особое внимание выбору метода наименьших квадратов, соответствующего особенностям структуры неопределенности данных в каждом конкретном случае. Поскольку упоминаемые методы хорошо описаны в технической литературе, а программное обеспечение, которое их реализует, доступно, они не описаны в настоящем стандарте.
1.3 Распространенные типы ковариационных матриц, связанных с данными калибровки, охватывают: (а) неопределенности данных отклика. (Ь) неопределенности и ковариации данных отклика, (с) неопределенности данных стимула и отклика и (d) неопределенности и ковариации данных стимула и отклика. Также рассмотрен случай, когда неопределенности данных неизвестны.
1.4 Приведены методы выбора степени полиномиальной калибровочной функции в соответствии с установленными критериями. Может быть получена ковариационная матрица, связанная с оценками параметров полиномиальной функции, как один из результатов используемых методов наименьших квадратов.
1.5 Для выбранной полиномиальной функции в настоящем стандарте описано использование оценок параметров и связанных с ними ковариационных матриц для прямого и обратного вычисления. Кроме того, в стандарте описано, как могут быть использованы положения Руководства ISO/IEC 98-3:2008 (GUM) для определения соответствующих стандартных неопределенностей.
1.6 Рассмотрены способы учета некоторых ограничений (например, полином должен проходить через начало координат), а также использование преобразований переменных, которые могут приблизить калибровочную функцию к полиномиальной. Рассмотрена также «смена ролей» переменных.
1.7 Использование настоящего стандарта иллюстрируют примеры из нескольких областей науки об измерениях.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты (для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных — последнее издание (включая все изменения)]:
Издание официальное
ISO/IEC Guide 98-3:2008. Uncertainty of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM: 1995) (Неопределенность измерений. Часть 3. Руководство по выражению неопределенности измерения (GUM:1995))
ISO/IEC Guide 99:2007 (corr. 2010), International vocabulary of metrology — Basic and general concepts and associated terms (VIM) (Международный словарь no метрологии. Основные и общие понятия и соответствующие термины (VIM))
3 Термины и определения
В настоящем стандарте применены термины по Руководству ISO/IEC 98-3:2008 и Руководству ISO/IEC 99:2012. а также следующие термины с соответствующими определениями.
Терминологические базы данных ISO и IEC доступны по следующим интернет-адресам:
- электронная база IEC Electropedia по адресу: http://www.electropedia.org/;
- электронная платформа ISO с функцией онлайн-просмотра терминов по адресу: http://www.iso. org/obp.
3.1 неопределенность измерений (measurement uncertainty): Неотрицательный параметр, характеризующий рассеяние значений величины, приписываемых измеряемой величине на основании используемой информации.
(Руководство ISO/IEC 99:2007 (изм. 2010). 2.26. модифицировано — Примечания 1—4 были удалены.)
3.2 стандартная неопределенность измерений, стандартная неопределенность (standard measurement uncertainty, standard uncertainty): Неопределенность измерений (3.1), выраженная в виде стандартного отклонения.
[Руководство ISO/IEC 99:2007 (изм. 2010). 2.30.)
3.3 ковариационная матрица измерения, ковариационная матрица (measurement covariance matrix, covariance matrix): Симметричная положительно определенная матрица размерности, связанная с вектором оценок размерности, содержащая по диагонали квадраты стандартных неопределенностей. связанных с компонентами вектора оценок, а вне диагонали — ковариации, связанные с парами компонентов вектора оценок.
Примечание 1 — Ковариационная матрица измерений Vx размерности N*N. связанная с оценкой х векторной величины X. имеет вид
Vx т
u(*i.*i) и(хьхы) u(xN.x,) ... u{xN,xN)
где u(x(>x.) = и*(х) — дисперсия (квадрат стандартной неопределенности), связанная с хг а и{х^х.) — ковариация пары х. и х, и{х^х-) = 0. если элементы X. и X вектора X некоррелированы.
Примечание 2 — Ковариационную матрицу также называют дисперсионно-ковариационной матрицей.
[Руководство ISO/IEC 98-3:2008/Доп. 1:2008, 3.11 (определение матрицы неопределенности). модифицировано — определение изменено, примечание 2 исключено, примечание 3 стало примечанием 2. изменено.)
3.4 корреляционная матрица (correlation matrix): Симметричная положительно определенная матрица размерности N*N, связанная с вектором оценок векторной величины размерности W* 1, содержащая корреляции, связанные с парой компонентов вектора оценок.
Примечание 1 — Корреляционная матрица Rx размерности N*N. связанная с оценкой ж векторной величины X. имеет вид
r(x,,Xi)
r(xWlx,)
'■(x1,xw)
/■(Xw.Xw)
где i\xfx) = 1 и rty.xp — корреляция, связанная с парой х, и хЕсли элементы X) и Х} вектора X не коррелированы. r{xfx) = 0.
Примечание 2 — г(х,.Ху) — также называют коэффициентом корреляции.
Примечание 3 — Rx связана с Vx (см. 3.3) соотношением
V, = DxR,D,'
где Dx — диагональная матрица размерности N * N с диагональными элементами ц(х,).....u(xN). Эле
мент с индексами (/. j) в Vx имеет вид:
= ^х^х/)и(х.)и(х).
[Руководство ISO/IEC 98-3:2008/Доп.2:2011. 3.21, модифицировано — определение изменено, примечания 4 и 5 исключены.]
3.5 модель измерений (measurement model): Математическая связь между всеми величинами, о которых известно, что они причастны к измерению.
[Руководство ISO/IEC 99:2007 (испр. 2010), 2.48. модифицировано — примечания 1 и 2 исключены.]
3.6 калибровка (calibration): Операция, в ходе которой при заданных условиях на первом этапе устанавливают соотношение между значениями величин с неопределенностями измерений, которые обеспечивают эталоны, и соответствующими показаниями с присущими им неопределенностями, а на втором этапе на основе этой информации устанавливают соотношение, позволяющее получать результат измерения исходя из показания.
Примечание 1 — Калибровка может быть выражена в виде утверждения, калибровочной функции, диаграммы калибровки, калибровочной кривой или таблицы калибровки. В некоторых случаях она может включать аддитивную или мультипликативную поправку к показаниям с соответствующей неопределенностью (3.1).
Примечание 2 — Калибровку не следует путать ни с регулировкой измерительной системы, часто ошибочно называемой «самокалибровкой». ни с верификацией калибровки.
Примечание 3 — Часто только первый шаг в приведенном выше определении принимают за калибровку.
[Руководство ISO/IEC 99:2007 (испр. 2010), 2.39.]
3.7 интервал стимула (stimulus interval): Интервал значений переменной стимула, на котором определяют калибровочную функцию.
3.8 стимул (stimulus). Величина, результатом измерения которой с помощью измерительной системы является отклик (3.9)\
3.9 отклик (response). Величина, представляющая собой результат измерения стимула с помощью измерительной системы'.
3.10 обратное вычисление (inverse evaluation): Определение значения стимула, соответствующего значению отклика на основе использования калибровочной функции.
3.11 прямое вычисление (direct evaluation): Определение значения отклика, соответствующего значению стимула, на основе использования калибровочной функции.
4 Обозначения
В настоящем стандарте использованы следующие обозначения.
4.1 Величина, значения которой обеспечены эталонами, называется независимой переменной (или стимулом) х, а величина, описываемая значениями, показываемыми измерительной системой, называется зависимой переменной (или откликом) у.
’ По отношению к калибровочной функции стимул представляет собой независимую переменную, а отклик — зависимую переменную.
Я, -
4.2 х( и у — измеренные значения декартовых координат /'-й точки (х., у.), / = 1.....m в наборе из т
данных калибровки. Часто используют векторные и матричные обозначения. Значения х, и у обычно представляют в виде векторов, где «Т» означает транспонирование:
* = 1*1.....хт]т.у = [у,.....ут]\
Матрицу или вектор, состоящие из нулей, обозначают 0.
4.3 Истинные значения координат /-й точки (которые могли бы быть получены при абсолютно точном измерении) обозначены ^ и Пг Измеренные значения точек в декартовых координатах и соответствующие истинные значения, связаны зависимостью:
* Г У Г П> + в;.
где dj и е, — ошибки х, и у, соответственно. Ошибки неизвестны, но часто могут быть определены их оценки.
4.4 Стандартные неопределенности, связанные с х, и у., обозначают о(х() и и(у) соответственно. Ковариацию, связанную с х, и х;, обозначают и(х,. х;). Аналогично, и(у. у) — ковариация, связанная с у,
"Уг
Примечание — В настоящем стандарте не рассмотрены перекрестные дисперсии u(xf у.), поскольку не было идентифицировано практическое применение калибровки, в которой установлены перекрестные дисперсии.
|
P(Xi,X,) - |
• U(XyXm) |
|
U(Xm,Xy) ■ |
• U(xm,xm) |
|
U(y,.y,) - |
■ и(У\-Ут) |
|
u(ym.y,) • |
• и(Ут’Ут) |
4.5 Информация о неопределенности в соответствии с задачей полиномиальной калибровки представлена матрицами Vx и Vy, каждая из которых имеет размерность т * т. Элементами матрицы являются дисперсии (квадраты стандартных неопределенностей) и*(х) = и(х-.х) и ^(у) = и(у»у) и ковариации и(хгх^) и и(у,у;). В (1) приведена ковариационная матрица, связанная с х. а в (2) — ковариационная матрица, связанная с у:
(1)
(2)
В конкретной задаче калибровки любая из матриц Vx и Vy может быть нулевой.
Примечание — Настоящий стандарт касается проблем, в которых и{х^ или и(у) различны (гетероскедастический случай).
4.6 Если все ковариации о(х^у) (/ * [) равны нулю. Vx представляет собой диагональную матрицу:
о2(х,)
(3)
- diag(uz(x,).....и[хт)].
и <хт)
Аналогично для и(у, у).
4.7 Элементы ниже ’ основной диагонали симметричной матрицы обычно не отображают (см. пример ниже)
|
1,2 |
-0,7 |
0.8 |
1.2 -0.7 |
0.8 | |
|
-0.7 |
2.5 |
0,5 |
S |
2.5 |
0.5 |
|
0.8 |
0.5 |
1.7 |
сим. |
1.7 |
4.8 Полиномиальную калибровочную функцию, связывающую у и х. обозначают рП(х), где п — степень полинома. Полином обозначают р„(х. а), если необходимо указать, что он зависит от п+1 параметра а = [э0.....ал}т.
4.9 Оценку величины q обозначают q . Значения модели, соответствующие точке данных (х-, у.), а именно, удовлетворяющие условию ф( = рп( х,. а). обозначают х, и
4.10 Функция, которую минимизируют для определения оценки параметров а полиномиальной функции, называется целевой функцией.
4.11 Несмотря на то. что значения данных в примерах представлены с заданным числом десятичных цифр после запятой, результаты вычислений иногда представляют с большим числом десятичных знаков, например, для сопоставления.
5 Стандарты, использующие полиномиальную калибровочную функцию
Ниже приведены другие стандарты, использующие полиномиальную калибровку.
a) ISO 6143:2006 [23] касается методов сравнения для определения и проверки состава калибровочных газовых смесей. Он содержит положения по определению (и использованию) «функций анализа» данных калибровки. Рассматриваемые функции анализа представляют собой полиномы степеней 1. 2 и 3. представляющие стимул как функцию отклика. Неопределенности допускаются в значениях данных стимула и значениях данных отклика. Ковариации допустимы в данных стимула, но не в данных отклика.
b) ISO 7066-2:1988 [24] охватывает основные методы определения и использования полиномиальных калибровочных функций при измерении расхода жидкости: оценка неопределенности при калибровке и использование приборов для измерения расхода. На языке настоящего стандарта ISO 7066-2:1988 рассматривает стандартные неопределенности, связанные со значениями у. и обратное вычисление.
c) ISO 11095:1996 [20] касается эталонных материалов с изложением общих принципов, необходимых для калибровки измерительной системы и поддержания этой системы в состоянии статистического управления. Он обеспечивает основной метод оценки линейной калибровочной функции, когда значения стимула точно известны.
d) ISO 11843-2:2000 [21] использует линейные калибровочные функции, когда стандартные неопределенности значений отклика постоянны или линейно зависят от стимула. ISO 11843-5:2008 [22] распространяет положения ISO 11843:2000 на нелинейный случай.
e) ISO/TS 28037:2010 [25] охватывает те же структуры неопределенности, что и настоящий стандарт. и рассматривает линейные калибровочные функции. Настоящий стандарт можно рассматривать как расширение документа ISO/TS 28037 на полиномиальные функции любой степени.
6 Данные калибровки и связанные с ними неопределенности
6.1 Калибровка состоит из двух этапов (3.6). На первом этапе устанавливают связь между значениями стимула, представляемыми эталонами, и соответствующими значениями отклика, полученными с помощью измерительного прибора. На втором этапе это соотношение используют для определения значений стимула на основе дополнительных значений отклика (обратное вычисление). Соотношение также позволяет определить значение отклика для дополнительного значения стимула (прямое вычисление). В настоящем стандарте упомянутое соотношение имеет форму полиномиальной калибровочной функции, содержащей набор параметров, оценки которых определяют по данным калибровки и связанным с ними неопределенностям.
Примечание — Настоящий стандарт не касается определения математической формы, с помощью которой значение стимула может быть определено точно по значению отклика. Такая форма известна в некоторых областях применения как функция анализа.
6.2 Калибровка измерительной системы должна учитывать приписанные неопределенности данных калибровки и все приписанные ковариации.
6.3 Приемлемая калибровочная функция удовлетворяет статистическому критерию на совместимость с данными калибровки и соответствующими неопределенностями. Во многих случаях она также должна быть монотонной (строго возрастающей или убывающей).
6.4 Для определения значения стимула (или отклика) и стандартной неопределенности, соответствующей заданному значению отклика (или стимула), используют стандартные неопределенности и ковариации, соответствующие оценкам параметров, и информацию о калибровочной функции.