Руководство по интерпретации кривых ВЭЗ МДС
Купить бумажный документ с голограммой и синими печатями. подробнее
Цена на этот документ пока неизвестна. Нажмите кнопку "Купить" и сделайте заказ, и мы пришлем вам цену.
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
В документе изложены приемы интерпретации кривых вертикального электрического зондирования методом двух составляющих (ВЭЗ МДС). Обеспечивающие определение электрических свойств горных пород и элементов залеганий их контактов (глубины, простирания, угла падения) с удовлетворительной для практических целей точностью. Предназначено для инженерно-технических работников изыскательских организаций.
Оглавление
Введение
1. Теоретические основы ВЭЗ МДС
Поле точечного источника постоянного тока на поверхности сред простейшего строения
Особенности деформации поля точечного источника тока и способы их изучении
2. Интерпретация кривых ВЭЗ, полученных над параллельно-слоистыми массивами
Однородное анизотропное полупространство с параллельной слоистостью
Двухслойное полупространство
Трехслойные среды
Четырехслойные параллельно-слоистые среды
Многослойные параллельно-слоистые среды
3. Основные закономерности изменения кривых ВЭЗ МДС над элементарными геоэлектрическими массивами (ЭГМ) с горизонтальными и наклонными границами раздела сред
Классификация ЭГМ
Основные закономерности изменения кривых двусторонних трехэлектродных D"P МДС над ЭГМ различного строения
Принципы построения номограмм для интерпретации кривых ВЭЗ МДС
Номограммы для определения элементов залегания наклоннослоистой среды
Номограммы для учета бокового влияния проводящих сред
Номограммы для определения простирания и истинного угла падения наклонных границ раздела
4. Некоторые закономерности изменения кривых ВЭЗ МДС над сложными геоэлектрическими массивами (СГМ) с горизонтальными и наклонными границами раздела
Основные закономерности формирования аномалий на кривых ВЭЗ МДС над СГМ, в которых ЭГМ чередуются в вертикальном направлении
Основные закономерности формирования аномалий на кривых ВЭЗ МДС над СГМ, в которых ЭГМ чередуются в горизонтальном направлении
Принципы систематизации сложных геоэлектрических массивов
5. Приемы интерпретации кривых ВЭЗ МДС, полученных над массивами различного строения
Качественная интерпретация кривых двусторонних трехэлектродных ВЭЗ МДС
Количественная интерпретация кривых и двусторонних трехэлектродных ВЭЗ МДС
Заключительный этап интерпретации
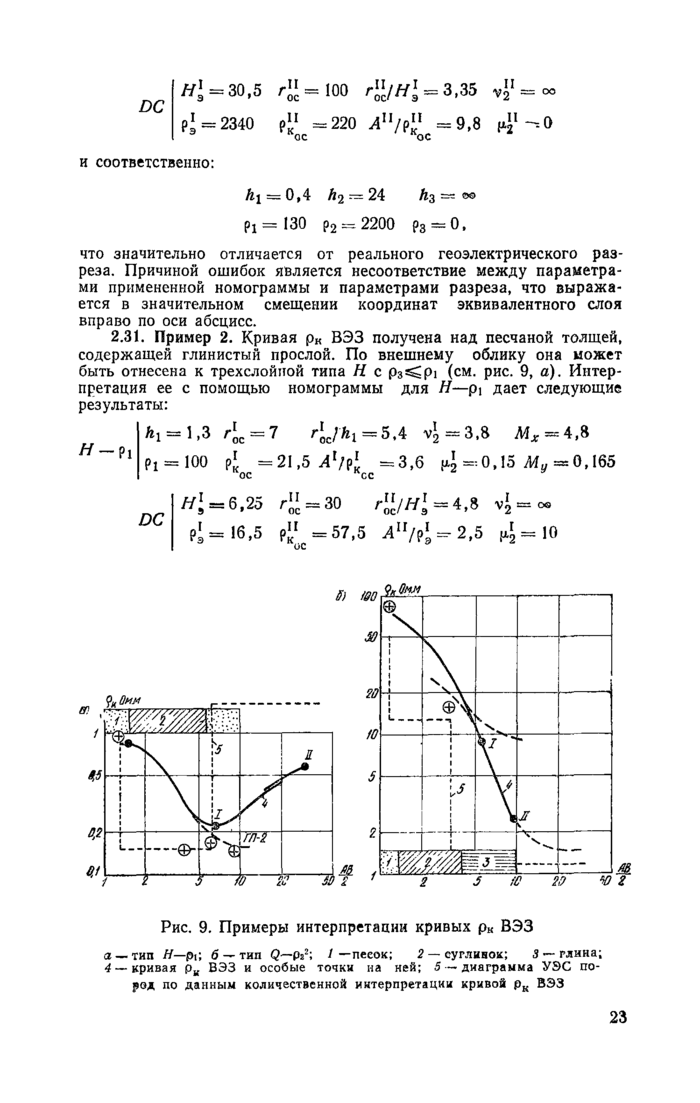
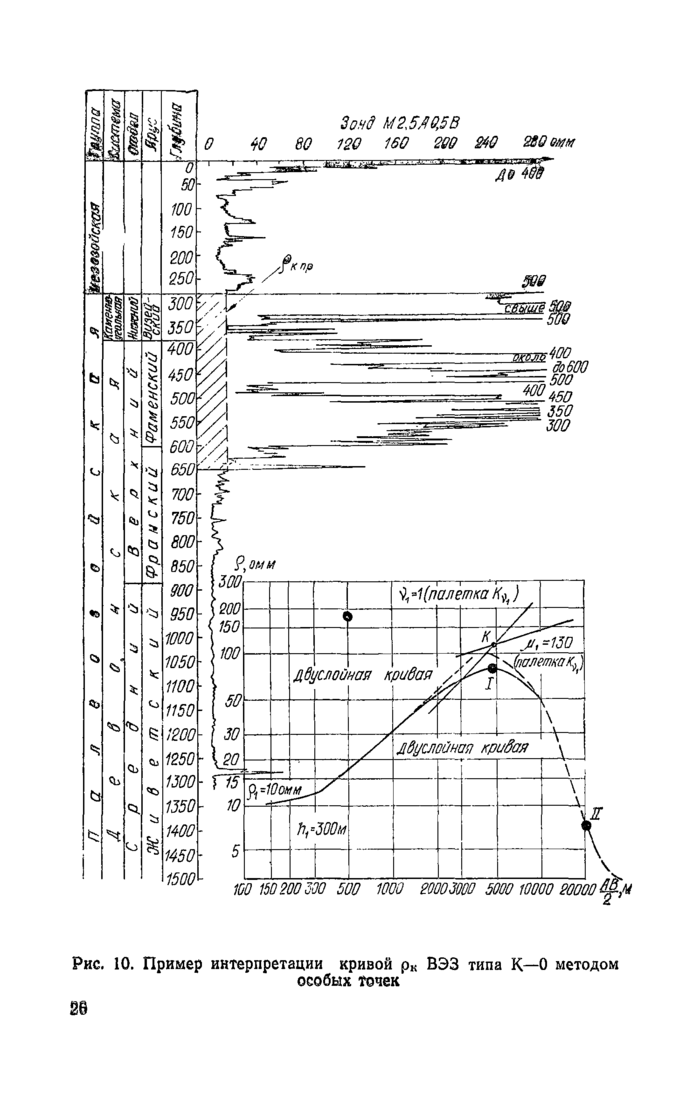
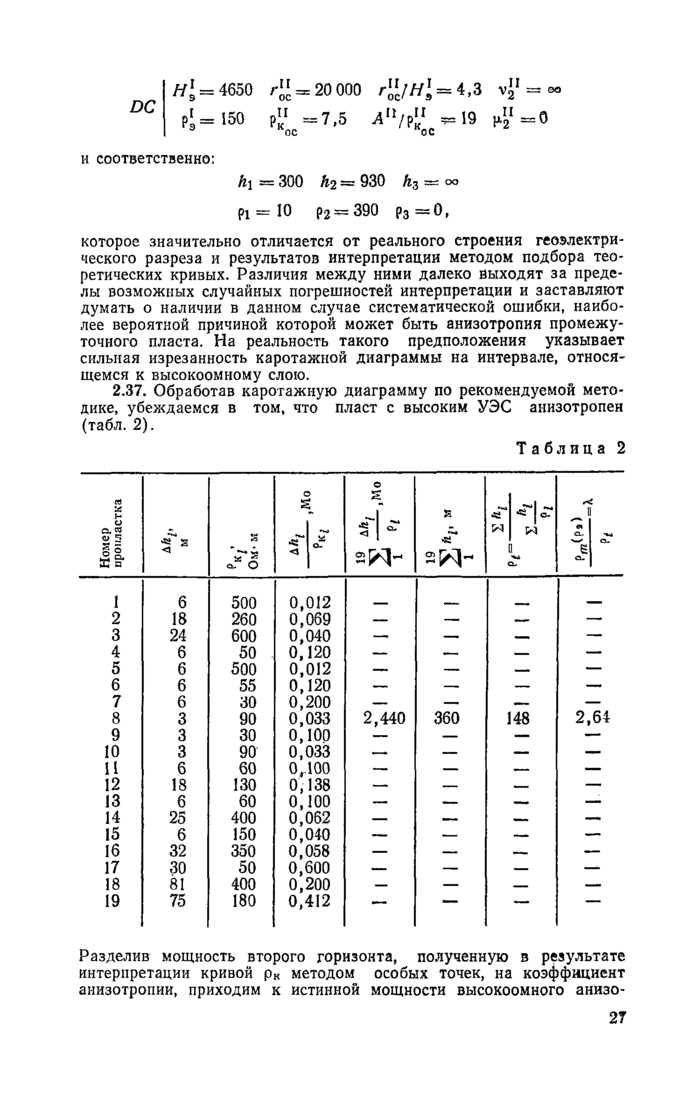
Примеры поэтапной интерпретации результатов зондирований
6. Некоторые вопросы методики ВЭЗ МДС
Критерии выбора размеров измерительных установок в связи с особенностями строения изучаемых массивов
Критерии выбора схем измерительных установок и способы измерений
Критерии размещения точек ВЭЗ на исследуемой территории
Техника полевых измерений
Приложение
| Дата введения | 01.01.2021 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот документ находится в:
- Раздел Строительство
Организации:
| Разработан | ПНИИИС Госстроя СССР | ||
| Издан | Стройиздат | 1984 г. | |
| Утвержден | ПНИИИС Госстроя СССР |
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6
стр. 7
стр. 8
стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20

стр. 21

стр. 22
стр. 23
стр. 24

стр. 25

стр. 26
стр. 27
стр. 28

стр. 29

стр. 30
пнииис
Госстроя СССР
Руководство
по интерпретации кривых ВЭЗ МДС
ПРОИЗВОДСТВЕННЫЙ И НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ПО ИНЖЕНЕРНЫМ ИЗЫСКАНИЯМ В СТРОИТЕЛЬСТВЕ (ПНИИИС) ГОССТРОЯ СССР
Руководство
по интерпретации кривых ВЭЗ МДС
Москва Стройиздат 1984
1
|
Pm 2л: |
(15)
[r 2 — 2ra cos у + ей)
(r2 -j- 2ra cos y + л2)1/2 J ’
со всеми вытекающими отсюда закономерностями изменения разности потенциалов и ко*эффициента установки в зависимости от угла у.
1.12. В случае наклонно-слоистой среды (ат^0°) формула для разности потенциалов не поддается непосредственному анализу, поэтому основные закономерности изменения разности потенциалов над анизотропной средой рассмотрим на примере теоретических кривых (рис. 4), вычисленных для постоянных параметров среды и размеров векторной установки.
1.13. Когда установка располагается вдоль или вкрест простира-
Д£/_
ния слоистости (ф=0°, 90°, 180° и т. д.), графики —-_L = /i(y) и
= f*i (Y) аналогичны графикам над изотропной или горизонтально-слоистой средой. В соответствии с так называемым парадоксом
анизотропии уровень значений на кривой —, полученной в направлении слоистости (qp =*0°, 180° и т. д.), выше, чем кривой, полу-ченной при ф=90°, 270°, и т. д. Произведение рк =—т посто’ янно при любых у и имеет значение рк=рт при ф=0°, 180°... и
_Pm_
[1 +(^2 — 1) sin2 а]1'2
при 9=90°, 270°...
Рк —
1.14. При любых других положениях оси установки относительно простирания слоистости (ф^О0, 90°, 180° и т. д.) графики А^т// имеют более сложный вид. Они перестают быть симметричными относительно оси ординат. Разность потенциалов на них достигает максимума при ф=й=0°, обращается в нуль при ф=И=90° и достигает некоторых положительных или отрицательных значений при ф=90°. Направление смещения экстремумов относительно оси ординат зависит от величины угла ф. При углах 0<ф<90° максимальные зна-
\и
чения на графике —j-^ = /i(Y) отмечаются слева от оси орди'
нат при отрицательных значениях угла поворота у» а нулевые и отрицательные значения разности потенциалов имеют место слева от оси ординат при положительных у. когда приемный электрод М находится справа от оси установки. При 90°^ф^180° (вторая чет-
верть) максимум на графике ——- =« f\ (y) смещается вправо по
оси абсцисс, а отрицательные и нулевые значения ДU^/I формируются при отрицательных у, когда электрод М размещается слева от оси установки. В третьей и четвертой четвертях характер измене-Д£7
ния графиков —j-L ~ /1 (y) тот же, что в первой и второй.
10
1.15. Произведение рк =—в этом случае непрерывно
изменяется по мере поворота приемной линии относительно оси установки, стремясь к —оо при V“=t90° и проходя через нуль на интервалах ~У0°<у<0° или 0<у<90° (рис. 5).
1.1 в. Можно заключить, что изменение рк обусловлено главным образом характером деформаций поля питающего электрода, а не изменением свойств среды, которые в каждой точке наблюдений постоянны и имеют положительные конечные значения. Полученный результат согласуется с представлениями о том, что кажущееся сопротивление является параметром поля, а не среды. В явной форме эта идея присутствует и в широко известном парадоксе анизотропии.
|
11 |
1.17. Особенности формирования величин и знаков ДС^// и, как следствие рк, можно объяснить, рассмотрев схему поля точечного источника тока на поверхности однородной анизотропной среды (рис. 4, а). Когда ф=0° или 90°, эквипотенциальные поверхности симметричны относительно оси установки. Максимальное число их пересекается приемной линией, ориентированной вдоль оси установки (у=0°). Электроды приемной линии попадают на одну экви-потенциаль при у=±90° и разность потенциалов между ними обращается в нуль. При ф=7^0° или 90° эквипотенциальные поверхности несимметричны относительно оси установки и пересекают ее под углами, отличающимися от прямого. Максимальное количество эквипотенциальных поверхностей пересекается приемной линией при Y^O0. Приемные электроды, ориентированные перпендикулярно оси установки (y=±90°), попадают на различные эквипотенциали, вследствие чего на них отмечается определенная разность потенциалов. Знаки и абсолютные величины этой разности потенциалов зависят как от величины угла ф между осью установки и простиранием слоистости, так от размещения приемных электродов относительно питающего (справа цли слева).
1.18. На основании анализа поля векторных установок можно сделать два чрезвычайно важных вывода, которые могут быть сформулированы следующим образом:
величины —рк являются
параметрами поля и, как следствие, векторными величинами, что предопределяет законы действия с ними при наложении полей от различных источников тока или возмущающих объектов;
Рис. 5. Зависимость величин
Д£7Т
Рк—— и К от угла поворота
приемной линии относительно оси установки
для изучения характера деформаций поля точечного источника тока или определения направления полного его вектора в заданной точке земной поверхности необходимо и достаточно измерить две его компоненты (составляющие).
1.19. Для обнаружения деформаций поля питающего электрода достаточно ввести в обычную схему измерительных установок в модификации сопротивления вторую приемную линию MnNn, располагающуюся перпендикулярно оси установки (см. рис. 1). Этой линии присвоено наименование «азимутальной». Приемная линия MtNt, ориентированная вдоль оси установки, названа «осевой».
1.20. Измерение по методу двух составляющих во многом сходно с методикой ЭП и ВЭЗ методом сопротивления. Разница заключается в том, что на каждой точке ЭП или разносе ВЭЗ берутся два замера разности потенциалов (по одному на осевой и азимутальной приемных линиях) и определяется сила тока в питающей цепи. Результаты измерений во всех случаях относятся к центру приемных линий, так как все приемы интерпретации разработаны нами только для этого случая. Дополнительно к этому при измерениях необходимо соблюдать ряд условий, который сводится к следующему:
на каждой точке профиля или каждом разносе ВЭЗ необходимо измерять не только величины осевой и азимутальной разностей потенциалов, но и их знаки;
в процессе всех измерений должен сохраняться принятый порядок взаимного расположения электродов осевой и азимутальной приемной линий. Мы везде будем пользоваться «правой» схемой расстановки закреплений приемных линий, при которой электрод Мп азимутальной приемной линии всегда находится справа от центра приемных линий, если обратиться лицом к электроду Mt осевой приемной линии. При таком положении второй осевой электрод Nt должен находиться сзади от наблюдателя, а второй азимутальный электрод Nn — слева от него;
во время измерений на -одной точке ЭП или одном разносе ВЭЗ полярность тока в питающей цепи не должна меняться;
на каждой точке профиля или каждом разносе ВЭЗ электроды осевой приемной линии должны размещаться строго по оси установки, а электроды азимутальной приемной линии — строго на перпендикуляре к ней. Ошибки в расстановке приемных линий не должны выходить за пределы ±1—2°.
1.21. Все требования обусловлены особенностями распределения поля питающих электродов установок на поверхности сред с наклонными границами раздела. Нарушение правил может сделать невозможной интерпретацию результатов наблюдений по методу двух составляющих или привести к крупным ошибкам в оценке' строения и свойств изучаемой среды.
1.22. При соблюдении перечисленных выше условий осевая разность потенциалов положительна, если электрод Mt располагается ближе к источнику тока с положительной полярностью, чем электрод Nt. Объясняется это тем, что электрод Mt попадает, как правило, на эквипотенциальные поверхности с большими положительными значениями по сравнению с теми, на которых находится электрод Nt. Знак азимутальной разности потенциалов переменен и в значительной степени зависит от особенностей строения среды и ориентировки оси установки относительно наклонных геоэлектрических границ.
Принимая это во внимание, условимся считать истинным знаком осевой разности потенциалов знак «плюс», а истинным знаком азимутальной разности потенциалов тот знак который возникает при правой расстановке азимутальных приемных электродов по отношению к источнику тока с положительной полярностью.
1.23. Это правило справедливо в подавляющем большинстве случаев. Однако, как показывает теория и практика, возможны такие деформации поля, при которых истинным знаком осевой разности потенциалов и соответственно кажущегося сопротивления будет минус. В частности, такое явление имеет место при профилировании или зондировании дипольной или трехэлектродной градиент-установ-кой над шологонаклонным хорошо проводящим пластом при неглубоком. залегании его верхней границы. В таких случаях истинные знаки осевой и азимутальной разности потенциалов могут быть определены лишь при условии, что в процессе всех измерений сохраняются полярность тока в питающей цепи и правая расстановка приемных электродов.
1.24. Легко убедиться в том, что перемена полярности тока в питающей цепи, или, что равноценно, одновременный поворот обеих приемных линий на 180°, вызывает одновременное обращение знаков осевой и азимутальной разностей потенциалов, но не отражается на их соотношении. Так, если оба знака были положительными, то после одной из указанных выше операций они станут отрицательными, но будут по-прежнему одинаковыми. Тем самым создается предпосылка для того, чтобы восстановить истинный знак азимутальной разности потенциалов по знаку осевой независимо от полярности тока в питающей цепи или размещения приемных линий по отношению к питающей. Для ее реализации необходимо в процессе всех измерений постоянно сохранять принятую правую схему размещения осевых и азимутальных приемных электродов относительно друг друга. Истинный знак азимутальной разности потенциалов устанавливается путем одновременного изменения знаков осевой и азимутальной разностей потенциалов, в результате которого осевая разность потенциалов должна стать положительной. Определение истинных знаков по наблюдаемым приведено в табл. 1.
|
Таблица 1 | ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
13
2, ИНТЕРПРЕТАЦИЯ КРИВЫХ р„ ВЭЗ, ПОЛУЧЕННЫХ НАД ПАРАЛЛЕЛЬНО-СЛОИСТЫМИ МАССИВАМИ
2.1. Понятие горизонтально-слоистые среды часто вводит в заблуждение геологов при обсуждении результатов интерпретации кривых рк ВЭЗ, особенно, если последние получены в условиях пересеченной местности. Удобней использовать понятие о параллельнослоистой среде, в которой границы залегают параллельно земной поверхности исследуемой территории.
2.2. К наклонно-слоистым относятся среды, в которых границы слоев залегают параллельно друг другу, но наклонены относительно земной поверхности.
2.3. Присутствие в массиве слоев, границы которых залегают параллельно земной поверхности, можно однозначно установить лишь по данным кругового ВЭЗ методом сопротивления, крестового ВЭЗ МДС симметричной установкой или единичного ВЭЗ МДС двусторонней трехэлектродной или дипольной установкой. В первом случае признаком параллельно-слоистой среды будет полное совпадение всех кривых рк ВЭЗ, полученных на одной точке в различных направлениях; во втором — полное совпадение крестовых кривых рк
Шп
при нулевых значениях ~ на всех разносах питающих электроде/ t
дов в обоих направлениях; в третьем — полное совпадение кривых
Шп
рк для правой и левой установок при нулевых значениях ~ ~.
Ш t
2.4. При интерпретации кривых рк ВЭЗ МДС удобно пользоваться уже известной классификацией параллельно-слоистых сред, в основу которой положена последовательность чередования в разрезе сверху вниз слоев с различными УЭС. При этом любой многослойный разрез расчленяется на трехслойные элементы, число видов которых равно четырем. Это так называемые трехслойные среды типов ЛГ(Р1<Р2, Р2>Рз)- <?(Р1>Р2>Рз). н (Pi > Р2. Р2 < Рз). А( pj< <Р2<Рз).
В некоторых случаях при обозначении трехслойных разрезов необходимо указывать значение УЭС третьего горизонта, что осуществляется путем добавления еще одного индекса к буквенному обозначению типа трехслойного разреза, например К—Рь Н — VН* А — ?2 и т. д.
Однородное анизотропное полупространство с параллельной слоистостью
2.5. В этом случае а=0 и рк=рт, откуда следует, что кривая ВЭЗ над параллельно-слоистым полупространством должна иметь вид прямой, параллельной оси абсцисс при нулевых значениях Шп
—тг~ на всех разносах питающих электродов. В связи с этим
Ш t
важно установить условия, при которых могут быть определены параметры анизотропной среды по данным электроразведки.
14
2.6. Известно, что:
-*=- = (1 +VH)1'2 ( 1 +~)_1/2 = Qi(Vi rt;
Рпр \ t4, /
Х = ——(I -Ь v^)1/2 (l ч- 1/2 = 02(V, ft),
Об)
где рпр — УЭС микропрослоев, хорошо проводящих электрический ток; рНПр — УЭС микрослоев, плохо проводящих электрический ток; 2/гпр — суммарная мощность хорошо проводящих микропрослоев; %hBap— суммарная мощность плохо проводящих прослоев;
Рнпр 21 ^ПР
а =- и v = .
Рпр 21 ^нпр
Систему из двух уравнений (16) можно изобразить в виде сетчатой номограммы (см. приложение, рис. 34), которая представляет собой два семейства кривых для различных постоянных значений
v и \i в прямоугольных координатах Х—% и У ~
Pm
Рпр
Характер
этой зависимости таков, что по любым двум из четырех входящих соотношений можно определить два других.
2.7. Величины рт, которая может быть получена в результате интерпретации кривой рк ВЭЗ, явно недостаточно для определения геоэлектрических параметров анизотропной среды с помощью номограммы. Задача становится разрешимой, если в результате обработ-
„ 21
ки каротажных диаграмм наити величины 9t = ■ , - и рпр»
VI hi
2d
Методика таких определений проста и изложена во всех руководствах по интерпретации данных ВЭЗ. Вычислив отношения
Pm
и I
по их величинам можно найти соотношение
Рпр Р t
мощностей проводящих и непроводящих прослоев в анизотропном
21 ^пр
массиве I v = I и УЭС непроводящих прослоев (рНнр = f^Pnp)*
нпр
Информация такого рода имеет большое значение при изучении трещиноватых и флишевых (слоистых) толщ с помощью зондирований.
Двухслойное полупространство
2.8. Особенности изменения кривых рк ВЭЗ над двухслойным полупространством хорошо исследованы. Теоретические двухслойные Рк
кривые — ВЭЗ сгруппированы в одну палетку, на которой всегда Pi
можно подобрать кривую, наилучшим образом совпадающую с интерпретируемой. Геоэлектрические параметры реальной среды вычис-
Рк
ляготся по параметрам найденной теоретической кривой — ВЭЗ.
. Pi
Такой способ интерпретации, получивший наименование метода под-
15
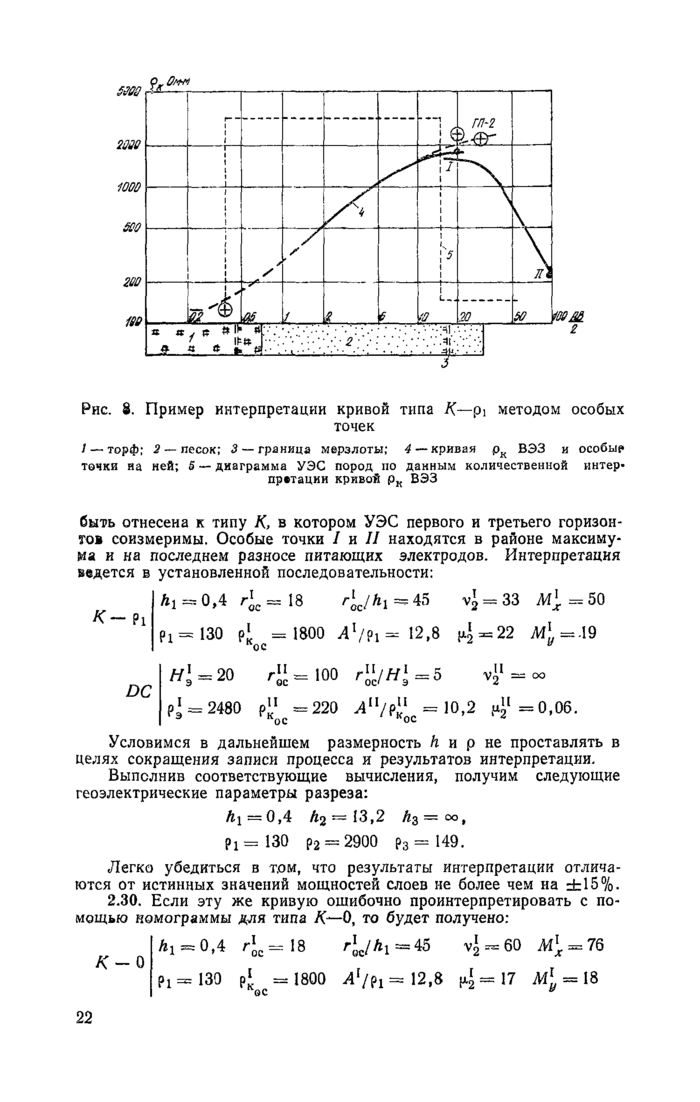
Рйс. 6. Схема определения особых точек на двухслойных кривых рк ВЭЗ
бора, наиболее распространен в электроразведочной практике, но не является единственным.
2.9. В целом ряде случаев, о которых речь пойдет в следующих разделах, целесообразней пользоваться методом особых точек. Установлено, что координаты точек на кривых рк ВЭЗ зависят от геоэлектрических параметров среды (Ай р! и рг) и величины действующего расстояния. На основании существующей зависимости составлена номограмма для определения параметров среды по величинам абсциссы и ординаты особой точки на интерпретируемой кривой рк.
В качестве координаты X взято отношение “^“.Вместо коорди-
пг
Рк
наты У — — по целому ряду -причин удобнее использовать соот-Pi
ношение
Рк
макс
Рк,
макс
-I.
(17)
кмин
МИН
характеризующее интенсивность влияния нижележащей среды при г о(* А
заданном —7— (рис. 6). По своей сути отношение “т- аналогич-
кл
Рк,
1 • ЛМИН
но интенсивности аномалии на графиках рк электропрофилирования. При Цг>1» тогда среда с высокими УЭС залегает снизу,
Рвмакс Ркос'
Р«мин — Pl>
Pi
(18)
Если высокоомная среда залегает сверху (}12<1), то рк =plf Ркмин Ркос*
А
(19)
-=р2^2. —)•
2.10. Зависимости (18) и (19) могут быть изображены в виде сетчатых номограмм (см. приложения, рис. 11), Каждая из них представляет собой семейство кривых для различных постоянных [12, построенное в прямоугольной системе координат с
/•ос
и Г
-(и-2> 1) или К = —
Р1 Рк,
(t»2< !)•
Параметры, необходимые для составления номограмм такого вида, могут быть получены в результате элементарного пересчета Рк
теоретических кривых — ВЭЗ.
Pi
2.11. Интерпретация кривы* рк с помощью номограмм производится следующим образом. Определив тем или иным способом ве-
АВ . Лгл
личины h\ и pi, произвольно выбирают значение гос= —
или ОВ) и находят для него рКос. Далее вычисляют отношения
г А А
—;-или —г- и по соответствующей номограмме определя-
«1 Pi ™ос
ют ц2.
2.12. Метод особых точек и рассчитанные для него номограммы
не имеют особого значения при интерпретации двухслойных кривых рк ВЭЗ, поскольку при определении величин hi и pi одновременно находится и значение р2. В свою очередь метод особых
точек становится единственным способом интерпретации двухслойных кривых рк, осложненных боковым влиянием проводящих сред. Большую помощь номограммы для двухслойной среды могут оказать при интерпретации многослойных кривых, правая ветвь которых не выходит на асимптоту. В этом случае вместо h\ и pi выступают мощность (Яэ) и УЭС (р0) эквивалентного слоя, а величины Ркос выбираются при максимальном разносе гос. Подробней этот вопрос рассматривается в следующем разделе.
Трехслойные среды
2.13. Традиционным способом интерпретации трехслойных кривых рк ВЭЗ является метод подбора, который дает хорошие результаты, если известен один из параметров промежуточного горизонта. Покажем возможности метода особых точек в этом отношении.
В формулу для кажущегося сопротивления над трехслойной
Рк г
средой входят пять независимых переменных — , — , v2, р.2 и р,3,
Pi «1
из которых первые две могут быть определены по интерпретируемой кривой без особых затруднений. В результате получаем систему из двух уравнений с неизвестными v2, Рг и
(20)
Рк/Pi = v25 Р2‘. Ра) .
r]h\ — ; V2; Р2; Рз| •
Система уравнений такого вида может быть изображена с помощью сдвоенных сетчатых номограмм, если одной из неизвестных переменных придать постоянные дискретные значения.
Рк
2.14. Величина неудобна для номографирования систе-Pl
мы (20) из-за плохого разрешения номограмм при малых v2 и р,2.
17
Поэтому на аналогии с двухслойной средой полезно использовать интенсивность аномалии на кривой рк.
|
1 гос |
\ | ||
|
Pi ~ |
(lip Ч2: ^ |
Ы; | |
|
Г0с |
/а | ||
|
hx " |
~F4 |
(—; v2; \ Pi |
Н-З 1 |
2.15. В случае массивов типов K(pi<p2, Рг>рз) и Л(р1<р2<рз) система (20) приобретает вид:
(21)
2.16. В массивах типов Я(р!>р2( Р2<Рз), и (3(р1>р2>Рз) Ркмии = Ркос. Ркмакс = Pi И система (20) может быть переписана
|
; v2; р-з; J; ; v2; ^2; р-з I■ |
следующим образом:
(22)
2.17. Для того чтобы ограничить число номограмм без ущерба для точности определения по ним параметров промежуточных горизонтов, необходимо придать дискретные значения отношению
Рз
Р-з = — , которое может быть найдено по правой асимптоте ин-Pi
терпретируемой кривой.
Далее необходимо установить единые правила выбора значений рКос и госна интерпретируемых кривых рк ВЭЗ. Решение этой задачи в значительной степени условно и зависит от строения и свойств трехслойных массивов и характера изменения кривых рк ВЭЗ над ними.
2.18. Когда на кривых рк ВЭЗ присутствуют максимум или минимум (кривые типа К или Я), особую точку следует приурочить именно к ним и по ней определить гос и рКос (рис. 7, тип К и Я).
2.19. В случае неявных кривых рк ВЭЗ, когда экстремум на них вырождается при определенных значениях v2 и |х2, особая точка находится по отрыву интерпретируемой кривой рк ВЭЗ от правой ее горизонтальной асимптоты (см. рис. 7, неявные типы К и Я).
2.20. Устойчивы критерии выбора особой точки на кривых рк ВЭЗ, полученных над разрезами типа А с бесконечно большим УЭС третьего горизонта. Значения гос и рКос следует брать в точке отрыва левой части интерпретируемой кривой от правой ее асимптоты, располагающейся под 45° к оси абсцисс (см. рис.- 7, тип А при |х3 = оо). Столь четкие критерии определения особой точки отсутствуют при любых других значениях jx3. С целью сохранения единообразия правил нахождения особых точек на кривых рк ВЭЗ над разрезами типа А условимся брать их в точке отрыва левой части интерпретируемой кривой от двухслойной теоретической наилучшим образом, т. е. наибольшим числом точек, совпавшей с правой ветвью
н асимптотой интерпретируемой кривой (см. рис. 7, тип Л, 1<|1з<°°).
18
|
L |
2.21. С аналогичными осложнениями приходится иметь дело при определении особых точек на кривых рк ВЭЗ, относящихся к разрезам типа Q. Здесь с целью сохранения единства правил нахождения особых точек условимся брать особую точку в месте отрыва левой части интерпретируемой кривой от двухслойной теоретической кривой, наилучшим образом совпавшей с правой ветвью и асимптотой интерпретируемой кривой (см. рис. 7, тип Q). Необходимо заметить, что некоторая неопределенность выбора особых точек на кривых рк в значительной степени компенсируется характером зависимости
гос А А
отношений —— ; - или —;- от va и рг, который обеспечивает
hi pi ”кос
получение устойчивых однозначных решений в сравнительно узком диапазоне изменения V2 и рг при изменении рКос и гос в довольно широких пределах.
2.22. В основу номограмм для трехслойных параллельно-слои
стых сред положены данные, полученные в результате соответствующей обработки и пересчета известных теоретических кривых. Сдвоенные сетчатые номограммы (см. приложение, рис. 12—17; 20—25), объединяющие два семейства кривых вида (21) или (22), построены в двух системах координат с общей осью и разными осями
Уi=—(“7-) и У2 для различных постоянных значений
Pi V °кос / 'Ч
Рг и р3. Каждая из номограмм снабжена типичной кривой рк ВЭЗ с указанным на ней положением особой точки.
19
Рекомендовано к изданию решением секции геофизики и инженерной сейсмологии Научно-технического совета ПНЙИИС Госстроя СССР.
Руководство по интерпретации кривых ВЭЗ МДС/ПНИИИС. — М,: Стройиздат, 1984. — 200 с.
Изложены новые приемы интерпретации кривых вертикального электрического зондирования методом двух составляющих (ВЭЗ МДС), обеспечивающие определение электрических свойств горных пород и элементов залеганий их контактов (глубины, простирания, угла падения) с удовлетворительной для практических целей точностью. Приведены примеры.
Для инженерно-технических работников изыскательских организаций.
Разработано ПНИИИС Госстроя СССР (канд. геол.-минерал. наук А. Н. Боголюбов, инженеры Н. П. Боголюбова, Е. Я. Мо з г а н о в а).
Табл. 7, ил. 138.
ПНИИИС ГОССТРОЯ СССР
РУКОВОДСТВО ПО ИНТЕРПРЕТАЦИИ КРИВЫХ ВЭЗ МДС Редакция инструктивно-нормативной литературы Зав. редакцией Л. Г. Вальян Редактор-М. А. Жарикова Мл. редактор Л. М. Климова Технический редактор М. В. Павлова Корректор Н. А. Беляева
Н/К
Сдано в набор 19.09.83. Подписано в печать 04.05.84. Т-02172
Формат 84X108V32. Бумага тип. № 3. Гарнитура? «Литературная».
Печать высокая. Уел. печ. л. 10,50. Уел. кр.-отт, 10,71. Уч.-изд. л, 12,7. Тираж 4300 экз. Изд. № XII—9640. Зак. 201. Цена 65 коп.
Стройиздат, 101442, Москва, Каляевская, 23а
Московская типография № 8 Согозполиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли, 101898, Москва, Центр, Хохловский пер., 7.
3202000000
Р —~ , ; -Инструкт.-нормат., И вып. — 74—83
047(01)—84
© Стройиздат, 1064
Номограммы такого вида обеспечивают однозначное определение
Гес
неизвестных величин v2 и ц2 по известным —— и
hx
Для этого определяют сначала величины hi и pi с помощью двухслойных, а если необходимо, то и трехслойных теоретических кривых рк ВЭЗ.
2.23. По соответствующим правилам выбирают особую точку на интерпретируемой кривой, находят значения гос и р.сос и вычисляют
Гос А А
отношения —-— и — или —-. Взяв номограмму, соответствую-
h\ Pi ГК0С
щую типу разреза и значению УЭС третьего горизонта, накладывают на нее прозрачный транспарант (кальку), на котором проводят оси координат номограммы. На осях ординат откладывают значения
—— и —I —-) в масштабе номограммы и фиксируют их точка-
h\ Pi \ Ркос /
ми. Поиски решения состоят в том, что транспарант перемещают вдоль оси абсцисс, сохраняя параллельность осей координат на транспаранте и номограмме. Этот процесс продолжается до тех пор, пока точки на осях ординат транспаранта не попадут на номограмме на кривые, имеющие одинаковые индексы р2. В этом положении центр осей координат транспаранта укажет на оси абсцисс номограммы величину v2, а индекс кривых — значение р2.
2.24. В силу эквивалентности разрезов Я и К по S и Т возможна некоторая неопределенность решения из-за совпадения одной
. /-ос А ( А \
пары значении —— и — —-1 с несколькими парами кривых
*1 Pi \ <Чс /
для различных р2. Поэтому, зафиксировав первое совпадение точек транспаранта с кривыми, имеющими одинаковый индекс на номограмме, необходимо продолжить перемещение транспаранта с тем, чтобы либо убедиться в единственности полученного решения, либо определить пределы неопределенности решения, устанавливая тем самым пределы действия принципа эквивалентности разрезов К и Я.
2.25. Специфика аномалий на кривых рк ВЭЗ над разрезами
К при рз>р1 и разрезами Я при p3<pt такова, что одна пара зна-
. А I А \ г1С чении — --J и —— может соответствовать двум парам ре-
Pi \ ”КМИН / h\
шеиия обратной задачи. Одно из решений имеет место при v2<l, когда на кривых рк ВЭЗ отсутствует экстремум; второе решение существует при v2>l и соответствует кривым рк ВЭЗ с отчетливо выраженным экстремумом. Учитывая это, выбор правильного решения из двух возможных должен производиться на основе анализа формы и амплитуды аномалии на интерпретируемой кривой.
2.26. УЭС третьего, опорного горизонта может быть определено по правой асимптоте интерпретируемой кривой. Если таковая отсутствует, то величина р3 может быть найдена способом, в основу которого положена возможность перевода трехслойного разреза в двухслойный путем замены первых двух сверху слоев одним эквивалентным с мощностью Яэ и с сопротивлением рэ. Значения Я0 и рэ определяют по вспомогательным номограммам LCK,. LCQ, LCH и LCA, которые хорошо известны и представляют собой два семейства кривых для дискретных значений v2 и построенных в системе координат (приложение, рис. 18, 26) X=l+v2 и К={г2. Коорди-
20
ВВЕДЕНИЕ
Большой диапазон изменения удельного электрического сопротивления (УЭС) горных пород в зависимости от их состава, строения и состояния создает самые благоприятные предпосылки для применения электроразведки вообще и вертикальных электрических зондирований (ВЭЗ), в частности для решения разнообразных задач, возникающих в геологической практике. Однако успехи электроразведки не соответствуют ее возможностям и достигнуты главным образом в районах с относительно простым геологическим строением и несложными гидрогеологическими и мерзлотными условиями. В более сложных случаях эффективность электроразведки резко снижается, причем причиной неудач, как правило, является присутствие в массиве пород геоэлектрических границ с различными элементами залегания. Наклонные контакты горных пород вызывают изменения (аномалии) на кривых рк ВЭЗ, нередко неотличимые от изменений, обусловленных влиянием горизонтальных границ. Применение в таких случаях приемов интерпретации, рассчитанных на простое слоистое строение среды, приводит к резкому снижению точности и надежности получаемых результатов.
Отсюда вытекает реальная потребность в таком способе электроразведки, который позволил бы при проведении ВЭЗ обнаруживать в массиве неоднородности с наклонными границами раздела и определять элементы залегания последних. Обобщая имеющиеся по рассматриваемой проблеме материалы, можно установить, что предложено пять способов измерения параметров электрического поля постоянного тока, необходимых и достаточных для обнаружения в разрезе негоризоитальных границ и оценки их элементов залегания. К ним принадлежат круговые измерения кажущегося сопротивления различными установками; измерения в модификации одной и двух составляющих, наблюдения квадратными, квадруполь-квадрупольны-ми и векторными установками.
Круговые измерения кажущегося сопротивления наиболее широко известны, но характеризуются низкой производительностью и высокой себестоимостью, которые ограничивают их применение. Все остальные способы по своей сути являются упрощенными или ус-ложненкыми вариантами измерений в модификации двух составляющих (в дальнейшем МДС), поэтому в настоящем Руководстве сосредоточено внимание на ВЭЗ МДС как на наиболее общем и вместе с тем достаточно простом способе исследования.
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ВЭЗ МДС
Поле точечного источника постоянного тока на поверхности сред простейшего строения
/Pi
2пг
1.1. Величины потенциала поля точечного источника тока на поверхности однородного изотропного полупространства определяются по формуле
где pi — УЭС среды; г — расстояние от источника тока до точки, в которой измеряется потенциал, или действующее расстояние.
3
1.2. Потенциал на поверхности однородного анизотропного полупространства равен:
гг_J У™ _!_ /94
2яг [1+(Х2—I)sin2¥sin2a:]1/2 ’ w
где рт — угр7"р7 — среднее удельное квадратическое сопротивление анизотропной среды; X = V?nl ?t — коэффициент анизотропии; рп — сопротивление среды в направлении, перпендикулярном слоистости среды; р*—сопротивление среды в направлении слоистости; а — угол падения слоистости относительно поверхности измерений; ср — угол между направлением г и простиранием слоистости.
1.3. Потенциал над двухслойной средой, граница раздела в которой параллельна поверхности измерений, определяется по формуле
р 2 — р ^
где кг2=-—коэффициент отражения; pi—УЭС первой от
?2 + Pi
поверхности среды; р2 —УЭС второй от поверхности среды; hi — мощность первой от поверхности среды.
|
I Pi 2лг |
1.4. Формула для потенциала на поверхности трехслойной параллельно-слоистой среды может быть представлена в виде
(4)
где qп — коэффициенты разложения в ряд, выражающиеся через коэффициенты отражения к\2 и к2з:
?2 Pi Р2 + Р1
#23 =
Рз Р2 Рз + ?2
1.5. Выражение для потенциала на поверхности среды, которая содержит вертикальный выходящий на поверхность контакт двух изотропных сред, может быть записано следующим образом в полярной системе координат ROq> с центром в источнике тока и осью R, направленной вдоль контакта:
а) при электроде А и точке М, находящихся над средой pi:
Uam==~^[1 +^2(4f-4'7sin?+ О ]’ ^
б) при электроде Л, находящемся в среде рь а электроде М — в Среде р2:
|
в) при электродах А и М, располагающихся в среде с рг: |
(6)
|
\ -1/2 |
(7)
Здесь йл—кратчайшее расстояние от электрода А до плоскости контакта.
Особенности деформаций поля точечного источника тока и способы их изучения
1.6. Векторные установки. Присутствие в массиве негоризонталь-иых границ раздела сред существенно изменяет форму поля постоянного тока на дневной поверхности по сравнению с нормальным полем над однородной изотропной средой. Наличие деформаций поля па дневной поверхности, их характер и степень можно определить, если в процессе измерений положение питающих электродов и центра приемных линий закрепить на местности и менять лишь угол у между приемной линией и осью установки. Такие установки названы «векторными» (рис. 1, 2).
1.7. Условимся под осью установки понимать прямую, проходящую через разнополярные питающие электроды. В случае трехэлектродных градиент-установок осью будет являться прямая, соединяющая питающий электрод и центр приемных линий.
1.8. На примере трехэлектродиой векторной установки AMN покажем изменение разности потенциалов Ш^{1 в зависимости от величины угла у при различных положениях оси установки на поверхности однородной изотропной и анизотропной сред. Примем, что к питающему электроду А присоединен положительный полюс источника питания; азимут между приемной линией и осью установки меняется так, что первый приемный электрод М находится всегда ближе к электроду А, чем второй электрод N. Положительные значения у условимся отсчитывать от оси установки по ходу часовой стрелки.
Воспользовавшись формулой (1), находим для однородной изотропной среды (рис. 2)
Выразив расстояния глм и rлN через параметры установки, полу чаем после упрощения
——I. = -1L, [(/-2 „ 2га соз Y 4* я2) 1/2 — (/2 + 2га cos у + а2) 1/2];
I /Д
(9)
где г — действующее расстояние установки, равное расстоянию от электрода А до центра приемных линий; а — полуразнос приемной линии.
5
M
|
A* |
S~ A*_
|
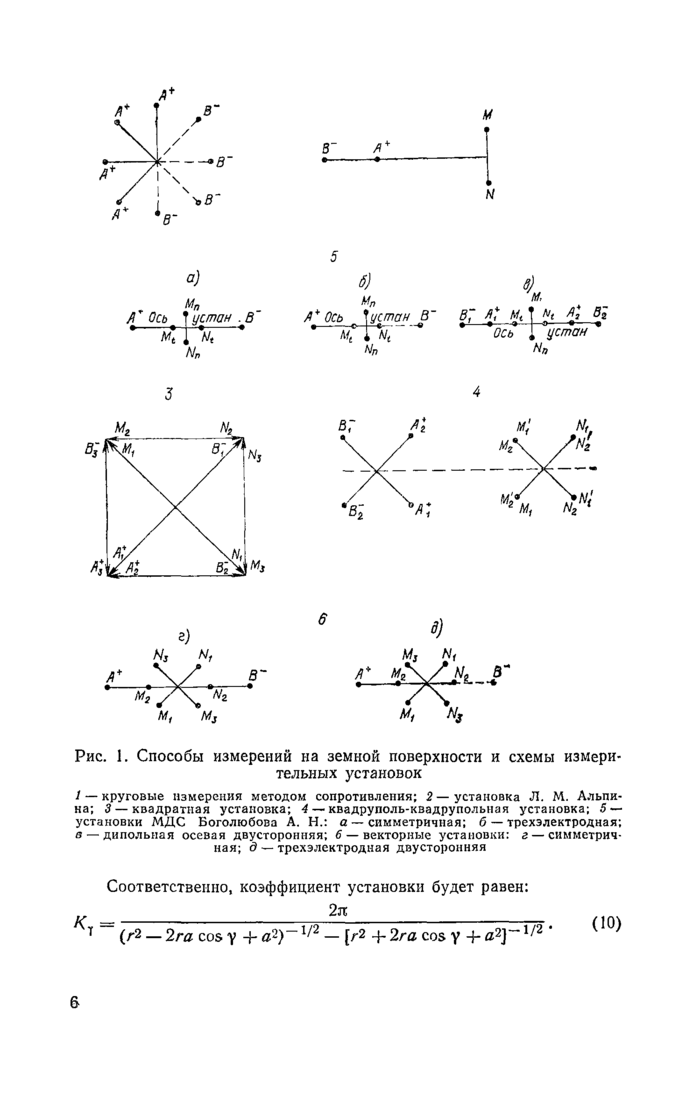
Рис. 1. Способы измерений на земной поверхности и схемы измерительных установок |
N
1 — круговые измерения методом сопротивления; 2 — установка Л. М. Альпина; 3 —квадратная установка; 4 — квадруполь-квадрупольная установка; 5 — установки МДС Боголюбова А. Н.: а — симметричная; б — трехэлектродная; в — дипольная осевая двусторонняя; 6 — векторные установки: г — симметричная; д — трехэлектродная двусторонняя
Соответственно, коэффициент установки будет равен:
(Ю)
______2я_
= (/*2 __ 2ra cos у -И а2)~1/2 — [/*2 -f 2га cos у 4- 1/2 *
§
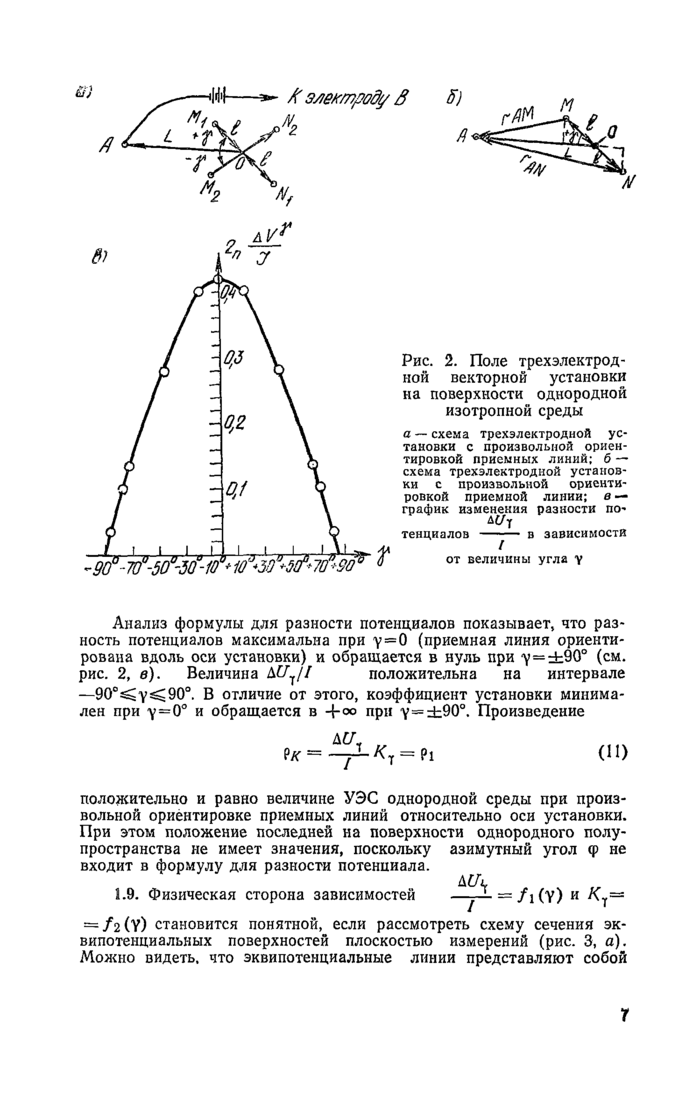
Рис. 2. Поле трехэлектродной векторной установки на поверхности однородной изотропной среды
а — схема трехэлектродной установки с произвольной ориентировкой приемных линий; б — схема трехэлектродиой установки с произвольной ориентировкой приемной линии; в — график изменения разности по-Д£/у
тендиалов - в зависимости
от величины угла у
Анализ формулы для разности потенциалов показывает, что разность потенциалов максимальна при у —0 (приемная линия ориентирована вдоль оси установки) и обращается в нуль при у=±90° (см. рис. 2, б). Величина bU^/I положительна на интервале
—90°^у^90°. В отличие от этого, коэффициент установки минимален при у=0° и обращается в +оо при у=±90°. Произведение
р *•=—-kt=pi (И)
положительно и равно величине УЭС однородной среды при произвольной ориентировке приемных линий относительно оси установки. При этом положение последней на поверхности однородного полупространства не имеет значения, поскольку азимутный угол ф не входит в формулу для разности потенциала.
Д
1.9. Физическая сторона зависимостей —~~~ = f\ (y) и дт=
= /г(у) становится понятной, если рассмотреть схему сечения эквипотенциальных поверхностей плоскостью измерений (рис. 3, а). Можно видеть, что эквипотенциальные линии представляют собой
У
О)
О)
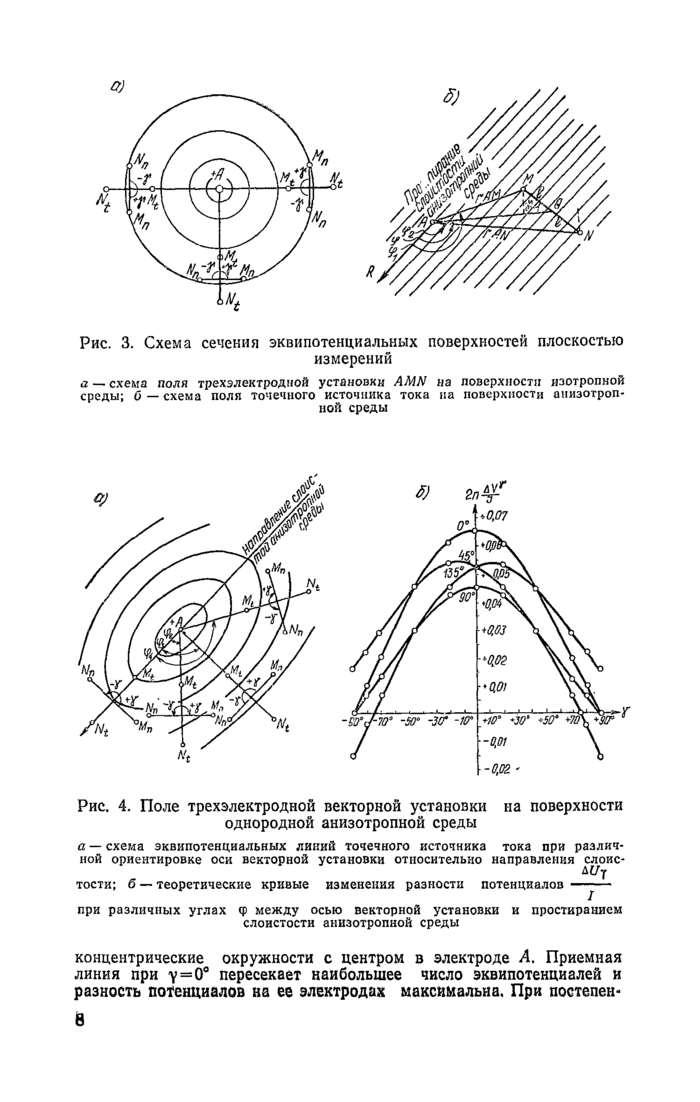
Рис. 3. Схема сечения эквипотенциальных поверхностей плоскостью
измерений
т
V
|
, *900 |
а — схема поля трехэлектродной установки AMN на поверхности изотропной среды; б — схема поля точечного источника тока на поверхности анизотропной среды
Рис. 4. Поле трехэлектродной векторной установки на поверхности однородной анизотропной среды
а — схема эквипотенциальных линий точечного источника тока при различной ориентировке оси векторной установки относительно направления слоис-
Д С/у
тости; б — теоретические кривые изменения разности потенциалов —-—
при различных углах Ф между осью векторной установки и простиранием
слоистости анизотропной среды
концентрические окружности с центром в электроде Л, Приемная линия при y=0° пересекает наибольшее число эквипотенциалей и разность потенциалов на ее электродах максимальна. При постепем-8
ном отклонении приемной линии от оси установки в ту или иную сторону число пересекаемых эквипотенциалей убывает и величина разности постепенно убывает, обращаясь в нуль при у=±90°, при котором приемные электроды попадают на одну эквипотенциальную поверхность.
1.10. Используя формулу (2), найдем выражение .для разности потенциалов над анизотропным полупространством при произвольном положении оси векторной установки на его поверхности:
_1_
(12)
ГАМ [1 + (Р — 1) sin2 <(м sin2 а]1/2
Oljv[1+(^2—1) sin2 <p/v sirl2 а]1/,г )’
где уц — угол между простиранием слоистости и направлением гЛм; ?лг — угол между простиранием слоистости и направлением г an (см. рис. 3, б).
Значения гАм> Галт» Ум и Уаг могут быть выражены с помощью параметров установки и ориентировки ее элементов относительно слоистости среды:
гам = (г2 — 2га cos у + а2)1/2\
гАм = (г2 И- 2га cos у + а2)1/2;
(13)
a sin у
Ум =<р 4- arctg-;
г — a cos у
a sin у
г + a cos у
?лг = — a*-ctg
^ ?т
I ~~ 2л
Подставив полученные значения в формулу для разности потенциалов, имеем
1
1/2
(г2 — 2ra ccs Y + я2)1/2 X I
[/ a sin y \ I
I + (X2 — I) sin2 ц sin2 [® + arctg-
V г — a cosy / J
(г2 2 a cos Y + л2)1/2 X
1
X 1 -h (X2 — 1) sin2 a sin2 f —- arctg-
L \ r + a cos Y
1.11. Для горизонтально-слоистых сред, когда а = 0°, полученное равенство приходит к виду, характерному для однородного изотропного полупространства: