Рекомендации по расчету каркасно-панельных общественных зданий с применением ЭВМ
Купить бумажный документ с голограммой и синими печатями. подробнее
Цена на этот документ пока неизвестна. Нажмите кнопку "Купить" и сделайте заказ, и мы пришлем вам цену.
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
В документе даны алгоритмы статического расчета полносборных зданий, а также зависимости для проведения проверок прочности и деформативности элементов несущей системы здания, предназначенные для разработки программ ЭВМ на всех этапах инженерных расчетов
Оглавление
1. Общие положения
2. Конструктивные характеристики и подбор элементов каркаса
3. Расчетные предпосылки
Расчетная модель и ее элементы
Нагрузки
4. Алгоритм статического расчета каркасно-панельных зданий на основе дискретно-континуальной модели
Дифференциальные уравнения и их модификация
Учет влияния продольного изгиба
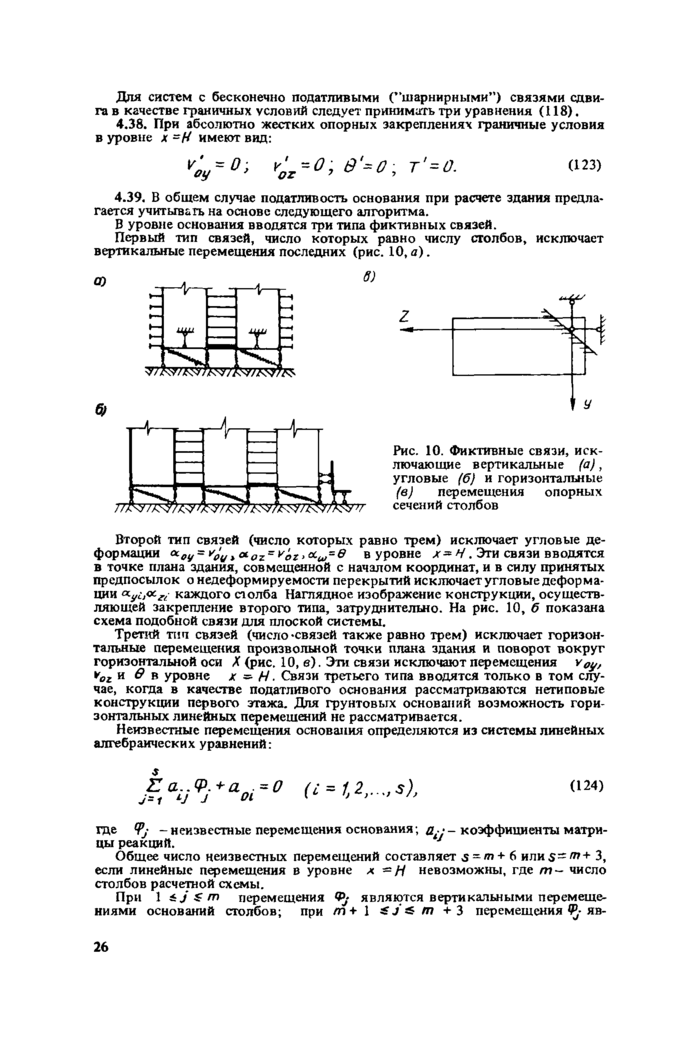
Граничные условия и учет податливости основания
Численный метод решения дифференциальных уравнений
5. Алгоритм расчета каркасно-панельных зданий на основе консольной модели
Упрощенные расчетные зависимости
Приближенный учет влияния продольного изгиба
Определение внутренних усилий в конструктивных элементах и деформаций здания
6. Проверка прочности конструктивных элементов
7. Программа ПРИКАЗ автоматизированного расчета зданий
8. Расчет дисков перекрытий
Приложение. Метод определения касательных напряжений для внецентренно-сжатых стержневых элементов
| Дата введения | 01.01.2021 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот документ находится в:
- Раздел Строительство
- Раздел Экология
Организации:
| Разработан | ЦНИИЭП торгово-бытовых зданий и туристских комплексов | ||
| Издан | Стройиздат | 1986 г. | |
| Утвержден | ЦНИИЭП торгово-бытовых зданий и туристических комплексов |
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26
стр. 27

стр. 28

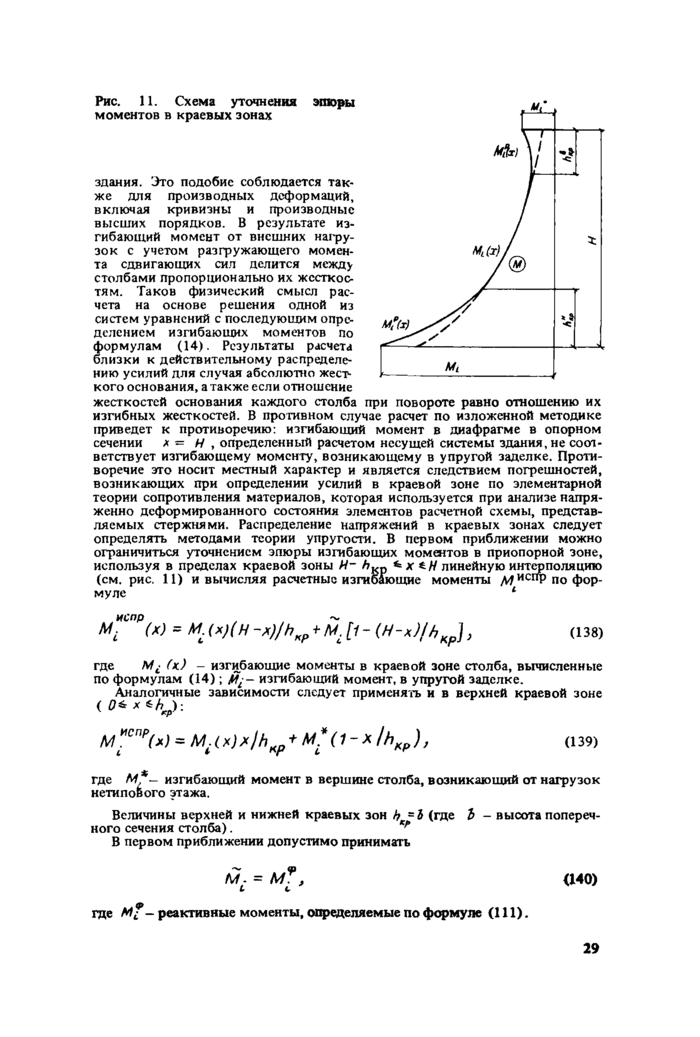
стр. 29
стр. 30
ЦНИИЭП торгово-бытовых здании и туристских комплексов Госгражданстроя СССР
Рекомендации
ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ
И ПРОЕКТНЫЙ ИНСТИТУТ ТИПОВОГО И ЭКСПЕРИМЕНТАЛЬНОГО
ПРОЕКТИРОВАНИЯ
ЗДАНИЙ ТОРГОВЛИ, ОБЩЕСТВЕННОГО ПИТАНИЯ,
БЫТОВОГО ОБСЛУЖИВАНИЯ И ТУРИСТСКИХ КОМПЛЕКСОВ (ЦНИИ9П ТОРГОВО-БЫТОВЫХ ЗДАНИЙ И ТУРИСТСКИХ КОМПЛЕКСОВ) ГОСГРАЖДАНСТРОЯ СССР
Рекомендации
по расчету каркасно-панельных общественных здания с применением ЭВМ
Москва Сгройнэдат 1986
|
A |
|
Рис. 5. Фрагменты расчетной схемы а - план; б - разрез |
4.5. С целью формализации расчетных зависимостей алгоритма, необходимой при использовании ЭВМ, вводится структурная матрица размером т* п , где т - число столбов в расчетной схеме; а ~ число связей сдвига. Элементам Cji структурной матрицы (j - номер столба, Ь — номер связи сдвига) задаются значения Сд = + 1, если связь с номером ( примыкает к столбу с номером j и вызывает в нем растяжение;^ = - 1, если связь с номером t примыкает к столбу с номером j и вызывает в нем сжатие; Zji — 0, если связь с номером £ не примыкает к столбу с номером j .
Структурная матрица определяет также правило знаков для сдвигающих сил 7* .
4.6. После решения системы дифференциальных уравнений усилия в отдельных элементах определяются по найденным значениям усилий в связях сдвига Т£, их интенсивности = Г/, перемещений *оу, v07., в , а также их производных.
Изгибающие моменты в столбах М ^ и Mz. вычисляются по формулам:
м . * - (к" ~еЪ.)в
' ZL ^ 02
мус =
(14)
где Ус »** - координаты столбов; изгибные жесткости столбов
4.7. В формуле (14) учтены известные закономерности дискретно-континуальной модели при абсолютно жестких перекрытиях:
к..- = к*. + 9z, ; ^ - б'б'..
У*
(15)
Аналогичные зависимости имеют место для первых производных перемещений
а также для производных высших порядков. 4.8. Продольные силы в столбах равны:
(16)
N. = -р. + г. е.. т .
L * к=1 к
(17)
При этом полная вертикальная нагрузка Рс столба определяется по формуле
Р£ = Р* +jpc ($)*$ • (18)
Для равномерно распределенной вертикальной нагрузки получаем
р. = Р.* + хр. . (19)
С L Г L
Положительными считаются растягивающие продольные силы в столбах. 4.9. Сдвигающие силы в соединениях (перемычках, закладных деталях и т.п.) вычисляются по формуле
АТ = Th
се >
(20)
где г = Т - интенсивность сдвигающих усилий в уровне данной связи; Лсв — шаг связей по высоте.
4.10. Для определения поперечных сил в столбах рекомендуется представить полный изгибающий момент в столбе AS- в виде суммы
мг = ' мр£ >
(21)
где Мр£ — изгибающие моменты в столбе от действия соответственно
горизонтальных и вертикальных сил.
Принимая значения полных изгибающих моментов по формуле (14) и учитывая, что вторая составляющая в формуле (21) равна:
= " *р! + Д Е£к Г* ~ Pi V ;
(22)
М
pzi = + ZZ В..Т - Р.1
н с Zl k-1 ik к t
е .
где > z и ~ расстояния от центра столба с до нулевой точки связи
/с ; после дифференцирования и преобразований получаем:
®У1 ~ )&zi ^Lk \ ^fiк*Pi ey*> >
(23)
2*
11
4.11. Дифференциальные уравнения, с помощью которых определяются неизвестные, вытекают из условий совместности деформаций и равновесия.
4.12. Уравнения первого типа (совместности деформаций) основаны на анализе полных взаимных смещений концов связей сдвига вследствие осевых и иэгибных деформаций столбов (рис. 6).
Из-за осевых деформаций столбов точки прикрепления связи / к столбам смещаются на величину (fL1, равную
<24>
где , Ас - осевые деформации соответственно растянутого и сжатого столбов, примыкающих к связи с.
Осевые деформации столбов определяются действием продольных сил на участке между сечениями х=const и
= / (Hj(Aj)d$ (J = t или J = c)f (25)
где A - осевая жесткость столба, вычисляемая по формуле (1).
Вследствие иэгибных деформаций столбов концы связи £ смещаются на величину л равную
^■г=~ V «и + гсс> (26)
где ос — углы наклона столбов в плоскостях, параллельных осям У и Z ;
~ расстояния от центров тяжести столбов t и С до нуле-bSVtAkh связи £ (см. рис. 5).
Углы наклона столба с координатами у*, г- связаны с перемещениями, отнесенными к началу координат, зависимостями:
°V = У'еу +в Ч' 2 * « = < - 9 У г • <27>
Подставляя значения формулы (27) в формулу (26), получаем перемещение с%2, равное
=~у* I - у* I “ В1 со. , (28)
iZ иу уь OZ zl ь >
где - относительные координаты связи, - секториальная коор
дината связи, вычисляемые по формулам:
|
Рис. 6. Взаимные смещения концов связи сдвига вследствие осевых (а) и иэгибных (б) деформаций столбов |
Если толщина столба пренебрежимо мала, то секториальная координата аа равна
Ч = Я lyi ~ £ lzc ' (31)
А л
где » х* — расстояния от начала координат до нулевой точки связи
С (см. рис. 5).
tf. =<?
(32)
£1
Полное взаимное смещение & концов связи i равно
В то же время полное смещение (Р* можно выразить через интенсивность сдвигающего усилия в связи f'.' Т/ и коэффициент податливости Л • по формуле (4) * 4 *
с2.=Л-Т'.. (33)
<• I с
Л. Т."=и. Z£ T'U,£ е Г-у!'
Приравнивая уравнения (32) и (33), учитывая уравнения (25) и (28) и введя обозначение i/А после однократного дифференцирования по х, получаем уравнение совместности деформаций в виде
__ _ I v" I
*k=i *кк Ск к оу ус 02 ZL
(34)
- Q-u>.-utPt +исРс (£ = 1,2,...,и).
Число уравнений (34) равно числу связей сдвига в расчетной схеме здания.
В уравнении (34) с, t ~ соответственно номера столбов сжатого и растянутого сдвигающей силой T-L . Выбор номеров сжатых и растянутых столбов осуществляется произвольно и фиксируется в структурной матрице.
При вычислении секториальной координаты связей по формуле (30) расстояния принимаются со знаками и считаются положительными,
если направление от. центра тяжести столба t до нулевой точки связи / совпадает с положительным направлением одноименных координатных осей. Аналогичное правило знаков распространяется на величины zci, yCi
4.13. Уравнения второго типа включают три уравнения, вытекающие из условий равновесия верхней части пространственной несущей системы здания:
М
п m m
|
m m fl |
+ М +£. Р.е .+£ М . у гч ^ l~i у*
где уол *0 - координаты точек приложения равнодействующих горизонтальных нагрузок; м; 9Q- - соответственно моменты и поперечные силы в столбах; М° , 0° — равнодействующие горизонтальных нагрузок в произвольных сечениях, определяемые по формулам (9), (10), (12). (13).
13
После преобразования и однократного дифференцирования уравнения равновесия приводятся к виду:
ш
оу у
D.+В'''д + £ T.'l- = Fu ;
У* г=1
У1
(36)
zl г
tti
90nD -6>V + /" В ~v В + ,
0 АУШ ** VQy QZ Zy ^ ^ l bjt
где с, п - соответственно номера и общее количество связей сдвига расчетной схемы; Vyj Dх - суммарные изгибные жесткости столбов расчетной схемы; суммарные жесткости изгибного и чистого кручения
столбов; F„ > - функции нагрузок здания, определяемые по форму
лам (39) ; £„2,XLy- суммарные вспомогательные жесткостные характеристики столбов.у *
4.14. Суммарные жесткости столбов расчетной схемы равны:
Яу=£в.
L ~~ 1
m
о ^ О *■
UJL
(37)
где В - изгибные жесткости отдельных столбов; - жесткости столбов
при чистом кручении; t, m - соответственно номера и общее число столбов расчетной схемы.
Суммарные вспомогательные жесткостные характеристики столбов ВХ(/ и J)yZ определяются по формулам: ’
Яу? =.| 62;Z;; Dzy * Д Вус У; • (38)
4.15. Свободные члены уравнений (36) равны.
где Qy, - равнодействующие горизонтальных нагрузок в произвольном
сечении х , определяемые по формуле (10) или (13); у0 , z0 - эксцентрицитеты этих равнодействующих относительно начала координат.
4.16. Три уравнения равновесия (36) совместно с уравнениями неразрывности деформаций (34), число которых равно числу связей сдвига п, образуют систему линейных дифференциальных уравнений, решая которую с учетом граничных условий, можно определить неизвестные сдвигающие усилия Г. и перемещения v^y, voz и 0, а также их производные: интенсивность сдвигающих усилий Т* г', углы наклона осоу- у' , осйг = v^z и оtrf&l кривизны Жау- Ядщг voz и =&'* а в необходимых случаях и производные более высоких порядков. Далее вычисляются внутренние усилия в любых конструктивных элементах и перемещения любых точек здания по формулам (14) - (23).
14
4.17. Возможны различные формы разрешающих дифференциальных уравнений.
Для конструкций, рассчитываемых без учета влияния продольного изгиба, порядок системы (36) можно понизить:
(40)
Суммарные моменты Му> Мх и бимомент горизонтальных и вертикальных нагрузок, действующих на здание, равны:
Му = * м‘+Е рр; М=М*+0*гх*M0^EP.ez.;
(M*+xQ*)z*
*(eyizi~eziyi)-
fn
+ZP.
i=1 *
(41)
X
z
ч
T
Рис. 7. К определению центра жесткостей
2
Центр
местности
I
I
+
I
I
I
ТУ
При переносе начала координат в центр жесткостей, расстояния и до которого от начала произвольной системы координат (см. рис. 7) равны:
ау ~ jVy , (42)
суммарные вспомогательные жесткостные характеристики J)yz и ZL обращаются в нуль, что приводит к разделению переменных в уравнениях (36) или (40). Например, уравнения равновесия (40) при переносе начала координат в центр жесткостей примут вид
уоЛ+^у = Му]
(43)
15
При этом возможна подстановка уравнений (43) в уравнения (34), что приведет к системе дифференциальных уравнений, позволяющих вычислить значения неизвестных Т. и € ; суммарный порядок этой системы равен
л+1: '
(44)
(45)
Если несущая система здания включает только элементы открытого профиля, жесткостями которых при чистом кручении можно пренебречь, уравнение (45) становится излишним и системы разрешающих уравнений включают п однотипных уравнений (44) при Ъ£ - 0, из которых определяются сдвигающие усилия Т; . Затем, используя уравнения (36), можно найти перемещения v и 8, а также их производныеос ~ v\3C- и" и т.д.
4.18. Обычно начало координат располагают в центре жесткостей, поскольку это позволяет упростить структуру уравнений. При разработке автоматизированных методов расчета достигаемое таким приемом упрощение не существенно. В то же время использование произвольной системы координат облегчает расчет немонотонных по высоте несущих систем вследствие унификации вычислительных операций в разных уровнях. Аналогичные преимущества имеет произвольная система координат при расчете зданий с учетом физической нелинейности материала методом упругих решений.
4.19. Для симметричных в плане зданий, деформация которых не сопровождается закручиванием, возможно применение плоской расчетной схемы. Сдвигающие силы при этом определяются из решения системы дифференциальных уравнений вида
(46)
4.20. Для консольной модели с плоскими диафрагмами задача расчета сводится к решению системы трех дифференциальных уравнений, вытекающих иа уравнений (40) при Т£ * Q, в которых неизвестными являются только перемещения: 1
(47)
При расположении начала координат в центре жесткостей, уравнения
(47) превращаются в уравнения с разделенными переменными:
УЧЕТ ВЛИЯНИЯ ПРОДОЛЬНОГО ИЗГИБА
4.21. Расчетная модель и все ее элементы принимаются в соответствии с пп. 3.1-3.6.
При этом условия совместности деформаций столбов и связей полностью сохраняются и дифференциальные уравнения типа (34) полностью справедливы.
4.22. Уравнения равновесия включают теперь дополнительные члены и имеют вид:
М9 + Е МуС +1 Mi + £ Г. 1£ = О -
l—f
ш*В
где М~ - дополнительные моменты, возникающие в столбах, вследствие продольного изгиба конструкций; 5“ - общее число всех элементов системы, несущих вертикальные нагрузки,, в том числе колонн каркаса, жесткость которых обычно во внимание не принимается;^^ - суммарные моменты горизонтальных и вертикальных нагрузок, принимаемые по формуле (41).
4.23. Значения дополнительных моментов, вызванных деформациями конструкций, равны:
В уравнениях (50) символом I обозначены функции, зависящие от деформаций системы (см. рис. 8)2 *
1У = voy ;
9 Л
4 = / [ voz (х> ~ yarte)]i*4 •' (51)
X
lu> = fce-w-o-<-%)]d?.
о
17
y(Zt
Рис. 8. К выводу уравнений равновесия при продольном изгибе
Н
Интегралы (51) зависят от параметра, их производные определяются выражениями:
С-**
(52)
4.24. При определении поперечных сил также необходимо учитывать продольную нагрузку. Представив полный изгибающий момент в столбе как сумму по формуле (21), во второй составляющей дополнительно учтем влияние продольного изгиба:
.=~kd е -Р (е . + v + 9z.)+p.z.I +p.l+ES.,T y-L', (53)
I 4 [ У1 °У ^ I ш "i У с~1 ск к v
* л PZL HiczL \ Yoz z (O ik к Zk
М =
pyt
В результате получаем следующие зависимости для определения поперечных сил Qy. и С,, в столбах:
п * = м* -- М*. = -(vw +В "z-)B ~+р.е . -/?. у 9 х +
ЫЦ1 ус myi { оу 4' гс ^i yL rt од
+p.z.B,x-P*v' + Р* 9 *z. - £ е..т/ У ;
'i / с (jy I i. С *=/ к tk
О . ~м'-~м'--~(у"' ~в”'у )В ■ +р. е .-pv'x +
Wzt zc ZC ' OZ УС у*- Г1 21 гс 02
f р. у. 0‘х - p*v' - Р*в'у . - Z Д;к T/z . .
гсу1 L QZ р с ^-у с к Аг *~zk
(54)
4.25. Подставляя уравнение (53) в первые два уравнения системы (49) и дифференцируя их с учетом уравнения (52), а значения формул (54) в третье уравнение системы (49), после преобразований получим следующую систему трех дифференциальных уравнений, выражающих условия равновесия
СД,+ С Ър.+9'Ьр.*+Е T'i . = F ;
У У* оу t С С с ус У9
18
9"'D
uj
Vй' в - у'" JD
ay -Vyz rOZ ■L’zy
+ v' EP.z.-
»y i = t t <-
oz
s
E
i=1
|
+ 9' P. U: |
(55)
где P£ - полные продольные силы во всех элементах, вычисляемые по фор* мулам (18) или (19); F - грузовые члены, принимаемые по формулам (39); т*. = у у?+ z? - плечо вертикальной нагрузки относительно начала координат. 4 * *
Система трех уравнений (55) совместно с уравнениями неразрывности деформаций
Л.т/=а £ £ Т-и Ее т-у‘ I --
* * *к=.1 ik к ск к оу yi
v”i. ~е'ш~
OZ ZC С
-“Л* “Л
(56)
образуют полную систему дифференциальных уравнений, решение которых позволяет определить усилия в элементах и перемещения пространственной системы здания с учетом деформированной схемы.
4.26. Уравнения деформированной схемы имеют ряд особенностей по сравнению с уравнениями (36).
Перенос начала координат в центр жесткостей расчетной схемы не приводит к полному разделению неизвестных перемещений в системе (55), которая принимает вид:
Для полного разделения перемещений необходимо выполнение дополнительных условий
£р 2. = £ Р.Ц.^О. (58)
4 * i=1 LI
Это означает, что влияние продольных сил вносит существенные особенности в работу пространственной несущей системы здания. Если условия (58) не выполняются, действие внешних нагрузок будет всегда сопровождаться поступательными перемещениями здания в направлении обеих координатных осей и закручиванием, а в расчетах на устойчивость будем получать единственное значение критических нагрузок, соответствующее изгибно-крутильной форме потери устойчивости. Эта же картина будет наблюдаться и для симметричных зданий с несимметричной вертикальной нагрузкой.
4.27. В некоторых важных для практических приложений частных случаях уравнения упрощаются.
19
УДК[69.056.53/.55:725Л]:68.1.3
Рекомендовано к изданию решением инженерной секции Научно-технического совета ЦНИИЭП торгово-бытовых зданий и туристских комплексов Госгражданстроя.
Рекомендации по расчету каркасно-панельных общественных зданий с применением ЭВМ/ЦНИИЭП торговобытовых зданий и туристских комплексов. — М.: Строй* издат, 1986. - 80 с.
Даны алгоритмы статического расчета полносборных зданий, а также зависимости для проведения проверок прочности и деформативности элементов несущей системы здания, предназначенные для разработки программ для ЭВМ на всех этапах инженерных расчетов.
Для инженерно-технических работников проектных и научно-исследовательских организаций.
Табл. 6, ил. 44.
Разработаны ЦНИИЭП торгово-бытовых зданий и туристских комплексов Госгражданстроя (канд. техн. наук Л.Л. Паньшин -разд. 1, 3-8, приложение; инженеры В.Э. Савранский - разд. 7, 8; Б.И. Волынский - разд. 2, 3. 6, 8; 0.0. Проценко - разд. 8; Е.Я Винокур - разд. 7).
Инструкт.-нормах., Т вып,- 126-86
3202000000 - 467
Р-------------
047 (01)-86
©Стройиэдяг, 1986
4.28. Для односвязных систем система дифференциальных уравнений состоит из двух уравнений, в которых неизвестными являются сдвигающая сила Т и перемещения у :
хт"- (и1 + и2)Т~ v"l = u1(P*+xpi)~ui (Р*+хрг); (59)
г’"1)+у'(Р*+Р*+хр^хр2)+ T'l = Q*+ Q°+Pl е1 +Р2 е2. (60)
Для анализа удобно преобразовать уравнения к безразмерному виду, введя безразмерную координату §=х!Н и безразмерные неизвестныеX*TWи , тогда уравнения односвязной системы приводятся к виду:
(62)
(63)
(64)
(65)
(66)
(67)
(68) (69)
В уравнениях (61), (62) штрихом обозначена производная по безразмерной координате ^ ; коэффициенты уравнений равны:
у = и ^ [(и1*иг)п *iz]/dx' ;
fi = D HD+Af zf +Агг\ ) \
V = H3zp./V; )>*=нг£р*/Л; i=1 1 1=1 1
<Pp=h* £ p.e.fjj; (P*=Q*H*ID;
r i&i t, *
4><f, = <}H3IP;
c = H-abs(i)(c,u1 +С2и2)/У, c*=Ha.bsdUc*u^c*u2)/X;
c. =p./ £ p- ; c*~P*/ZP*.
Граничные условия задачи в уровне $ = 1 при деформируемом основании можно получить также в безразмерной форме из уравнений (118) и
i Pi' ’ t i 11 = 1 *
(122):
w"m + w' = O', (70)
Х'+П°X - (1-fl)r2n',-nl>-St*)>* = 0, (71)
где т/£п,п*- коэффициенты податливости основания;
/77 = 2? /HR (72)
пв = НЫ*+и%)1л; (73)
п = abs(l)(c1u°-c2u%)/x; (74)
К* = abs(L)(c* и* -С*и°)/Х, (75)
где R - суммарная жесткость основания, вычисляемая по формулам (119), U - коэффициент, вычисляемый по формуле (122).
20
ОБЩИЕ ПОЛОЖЕНИЯ
1Л* Настоящие Рекомендации разработаны с учетом '’Указаний по рас* чету прочности, устойчивости и деформативности зданий с диафрагмами жесткости. Серия 1.020-1/83. Конструкции каркаса межвидового применения для многоэтажных общественных и производственных зданий. Выпуск 0-2” (М., ЦИТП, 1984).
1.2. Рекомендации содержат алгоритмы, необходимые исходные данные и методические указания по использованию специальных программ для ЭВМ по расчету пространственных несущих систем зданий с каркасом серии 1.020-1/83 и элементов этих систем.
1.3. Рекомендации ориентированы на применение дискретно-континуальной расчетной модели здания, содержат указания по формированию расчетной схемы применительно к конструктивным особенностям изделий серии 1.020-1/83, по назначению жесткостных характеристик элементов и связей, а также статический расчет с определением усилий в конструктивных элементах и стыках и расчет их прочности и Деформаций. Алгоритмы учитывают пространственное взаимодействие конструктивных элементов, деформированную схему сооружения и взаимодействие надземной части здания с деформируемым основанием. В Рекомендациях предусмотрена возможность последовательного упрощения расчетной модели, исходя из требований, предъявляемых к точности результатов на различных стадиях проектирования, и конкретных особенностей парка ЭВМ проектной организации.
1.4. В Рекомендациях рассмотрены вопросы использования программы комплексного расчета каркасно-панельных зданий ПРИКАЗ и специальной модификации программного комплекта ПРОКРУСТ для расчета дисков перекрытий.
1.5. Рекомендациии могут быть использованы при разработке автоматизированных методов проектирования полносборных каркасно-панельных зданий и механизации отдельных зтапов процесса проектирования на базе различной вычислительной техники.
2. КОНСТРУКТИВНЫЕ ХАРАКТЕРИСТИКИ И ПОДБОР ЭЛЕМЕНТОВ КАРКАСА
2.1. Основной конструктивной особенностью связевых каркасов, определяющей характер работы их несущих элементов, является нулевая жесткость узлов рам, не оказывающих существенного сопротивления горизонтальным перемещениям здания (рис. 1). Пространственная неизменяемость здания со свяэевым каркасом обеспечивается системой вертикальных несущих элементов - диафрагм жесткости, объединенных дисками перекрытий в единую пространственную схему. Диафрагмы жесткости воспринимают все усилия от нагрузок, вызывающих горизонтальные перемещения здания, а колонны и ригели рам - только вертикальную нагрузку.
2.2. Расчетные схемы элементов, составляющих каркас здания, могут быть представлены:
панели перекрытий и ригели - в виде разрезной однопролетной балки, нагруженной равномерно распределенной нагрузкой;
колонны — в виде многопролетной нсразрезной балки, опертой на диски перекрытий, загруженной продольными сжимающими силами и сосредоточенными изгибающими моментами, приложенными на опорах;
диафрагмы жесткости - в виде консольного вертикального стержня с продольными и поперечными нагрузками, приложенными в уровне дисков перекрытий. Диафрагмы жесткости считаются закрепленными из плоскости в уровне дисков перекрытий.
3
|
Рис. 1. Основной узел каркаса а - серии ИИ-04; б - серии 1.020-1/83; 1 - колонна; 2 - распорная панель перекрытия; 3 - многопустотные панели перекрытия; 4 - ригель; 5 - монтажные накладки |
2.3. Подбор панелей перекрытии производится сопоставлением действук>-щих на перекрытие расчетных нагрузок с нагрузками, определяющими несущую способность панелей различных марок.
Образование горизонтальных дисков с помощью панелей перекрытий обеспечивается сваркой связевых (межколонных и пристенных) Т1анеяей пе рекрытий между собой и ригелями, а также за счет тщательного эамоноли-чивания шпонок и швов между всеми элементами перекрытия. Соединения связевых плит обеспечивают восприятие диском растягивающих усилий, значения которых приведены в разд 8.
2.4. Подбор ригелей аналогичен подбору плит в тех случаях, когда ригели воспринимают равномерно распределенную нагрузку. В случаях когда на ригель действуют нагрузки, отличающиеся от равномерно распределенных, следует определить эквивалентную нагрузку и сопоставить ее с несущей способностью ригеля, приведенной в марке.
2.5. Колонны связевого каркаса работают в условиях, близких к условиям центрального сжатия. Поэтому в качестве прочностной характеристики принимается их несущая способность при действии сжимающей продольной силы, приложенной со случайным эксцентрицитетом = 1 см. Этим параметром можно воспользоваться при затружении колонн нагрузками, отличающимися от принятых в серии 1.020-1/83. При проектировании зданий с каркасом 1.020-1/83 поверочные расчеты, связанные с подбором колонн, производить не требуется, так как положение колонны в монтажной схеме каркаса здания однозначно определяется ее геометрическими размерами, что позволило и при проектировании колонн учесть их невыгодное загружение.
2.6. Диафрагмы жесткости представляют собой консольный вертикальный стержень с продольными (сжимающими) и поперечными силами.
Диафрагмы жесткости связевых каркасов состоят из сборных типовых стенок жесткости и колонн, соединяемых сваркой закладных деталей, и образующих единую конструкцию, воспринимающую горизонтальные и вертикальные нагрузки. Необходимо указать на известную терминологическую неточность, поскольку термин *’диафрагма” используется в рабочих чертежах изделий серии 1,020-1/83 для обозначения сборного стенового элемента, входящего в состав описанной конструкции комплексной диафрагмы. Излишне вводить специальное понятие, например, "пилон” или "устой”, как это сделано в некоторых работах. В настоящих Рекомендациях термин "диафрагма жесткости" относится к любым несущим элементам, в том числе, имеющим сложную форму сечения, которые обеспечивают пространственную неизменяемость здания. Чтобы подчеркнуть принципиальные особенности расчета и конструирования используется также термин "ядро жесткости", относящийся к элементам с замкнутым контуром.
4
|
Рис. 2. Конструкция сборных диафрагм жесткости а - серии ИИ-04; б - серии 1.020-1/83; 1 - сборные стенки жесткости; 2 - диафрагменные колонны каркаса; 3 - закладные детали; 4 - бетон зам оно ли-чивания; 5 - панели перекрытий; 6 - жесткий цементный раствор |
Конструкция сборных типовых диафрагм жесткости показана на рис.2. Основное отличие сборных железобетонных диафрагм жесткости серии 1.020-1/83 заключается в замене горизонтального монолитного стыка сборной стенки растворным контактным, что позволило резко упростить технологию его изготовления и монтажа.
Помимо сборных типовых диафрагм жесткости неизменяемость несущей системы зданий со связевыми каркасами могут обеспечивать различные нетиповые конструкции, в частности для высоких зданий - монолитные железобетонные диафрагмы и ядра жесткости. В отдельных случаях диафрагмы жесткости могут выполняться в виде несущих кирпичных перегородок, установленных на ригелях каркаса. Наружные кирпичные стены и сборные несущие и самонесущие стеновые панели выполняют функции диафрагм при условии обеспечения их полноценной связи с перекрытиями.
В подавляющем большинстве случаев диафрагмы жесткости являются составными конструкциями, включающими колонны каркаса и сборные (реже - монолитные железобетонные или каменные) стены или участки стен для диафрагм с проемами. Элементы диафрагм объединены связями (закладными деталями, анкерами, перемычками и т.п.), которые обеспе-
5
Рис. 3. Обобщенная конструктивная схема диафрагмы
1 - стенки жесткости; 2 - диафрагменные колонны каркаса; 3 - закладные детали
чивают их совместную работу. Обобщенная конструктивная схема диафрагмы представлена на рис. 3.
f 1
:::в>ешэ0
деформативность элементов, что в свою очередь отражается на напряженно-деформированном состоянии конструкций.
Связи и соединения обладают определенной податливостью, а их деформации оказывают заметное влияние на распределение усилий между эле-м ентам и ди афр агм и дефор м аций конструкции. Аналогичную роль играют надпроемиые перемычки. Горизонтальные швы диафрагм увеличивают
2.7. Основания зданий только в единичных случаях могут считаться абсолютно жесткими. Практически всегда они являются податливыми, в результате чего полные деформации здания возрастают, а внутренние усилия в несущих конструкциях существенно перераспределяются, особенно на нижних участках здания.
Конструктивные особенности зданий связевой системы можно учесть, используя различные расчетные модели и методы расчета.
В настоящих Рекомендациях излагаются методы расчета, базирующиеся на дискретно-континуальной модели, которая позволяет достаточно строго учесть все перечисленные особенности.
3. РАСЧЕТНЫЕ ПРЕДПОСЫЛКИ
Расчетная модель и ее элементы
3.1. Расчетная схема здания принимается в виде пространственной стержневой системы, состоящей из вертикальных элементов (столбов), соединенных непрерывно распределенными по высоте связями сдвига. Совместная деформация столбов в пространственной несущей системе здания обеспечивается дисками перекрытий.
3.2. Расчетная схема наиболее полно отражает конструктивные особенности здания, если каждый конструктивный элемент (колонна, входящая в состав сборной диафрагмы жесткости; вертикальный ряд сборных стен жесткости или простенков с проемами) рассматривается как самостоятельный столб расчетной схемы. Монолитные ядра жесткости замкнутого сечения или монолитные диафрагмы открытого профиля при формировании расчетной схемы разрезаются вертикальными фиктивными швами на отдельные плоские элементы.
3.3. Основными характеристиками столбов служат величины их осевых А и изгибыых В жесткостей. При этом для конструктивных элементов с горизонтальными растворными швами следует учитывать их повышенную
6
деформатив но сть вследствие податливости швов, вычисляя их жесткости по формулам:
Л = О) ВекшЬ°, (2)
где А0 и В9 - осевые и изгибные жесткости столбов, вычисленные как для монолитных железобетонных элементов; Аш - коэффициент, учитывающий снижение жесткости столбов в результате податливости растворного шва и равный:
= Г/(^Лш£г/Лэт), (3)
где Аш - податливость растворного шва, принимаемая по данным табл.18 ’’Инструкции по проектированию крупнопанельных жилых зданий” (ВСН 32-77/Госгражданстрой). -М., Стройиздат, 1978; Лэг- высота этажа.
3.4. В приближенных расчетах сборная диафрагма жесткости может рассматриваться как единый столб. При этом жесткость такого столба должна назначаться с учетом податливости соединений сборных элементов диафрагм (см. разд. 6). Возможна также укрупненная трактовка замкнутых ядер жесткости в качестве единого столба расчетной схемы (см. п. 5.1).
3.5. Связями сдвига, объединяющими столбы расчетной схемы, являются закладные детали сборных железобетонных элементов, анкеры и над проемные перемычки. В расчетной схеме зданий связи сдвига считаются непрерывно распределенными по высоте.
Деформативные свойства распределенных связей сдвига характеризуются коэффициентом податливости А, м^/кН, или м^/тс, равным:
А - Ahee , (4)
где Л - коэффициент податливости отдельного соединения на сварке закладных деталей или перемычки, м/кН; h св - шаг связей по высоте.
Для закладных деталей диафрагм серии 1.020-1/83 коэффициенты податливости можно с небольшим округлением принять одинаковыми для различных высот этажей А- 4,75ЛОг* м^/кН (4,75'10“^м2/тс) для соединений стенки с колоннами и У= 3»10“® м2/кН(3*10“* м/тс) - для соединений стенки со стенкой.
3.6. В практических расчетах возможно применение консольной расчетной модели, которая представляет собой частный случай дискретно-континуальной модели при абсолютно жестких связях сдвига. При этом, используя упрощения, вытекающие из абсолютной жесткости связей сдвига, при построении расчетных зависимостей действительную податливость соединений можно учитывать приближенно, например, с помощью коэффициентов условий работы. Алгоритмы для консольной модели описаны в разд. 5.
Нагрузки
3.7. В общем случае необходимо учитывать действие на здание горизонтальных и вертикальных нагрузок.
3.8. Горизонтальные (ветровые) нагрузки if распределены по высоте здания неравномерно в соответствии с эпюрой скоростного напора (рис. 4, а). Наиболее точно действительная эпюра скоростного напора аппроксимируется трапециевидной эпюрой, показанной на рис. 4, б. Параметры этой эпюры
(ординаты у и a<f) можно выразить через величины момента Н°(Н) и поперечной силы(ДН)в уровне основания здания высотой Н :
9
(5)
|
Рис. 4. Действительные (а) и расчетные (б, вf эпюры нагрузок |
a.= 6/(m~6)i (6)
т ~ HQ°(H)/M°<H). (7)
3.9. При эпюре ветровых нагрузок в форме трапеции усилия в любом уровне равны: г
q (х) = $(1-(1-а)х/н); (8)
М°(х) = 0,5ухг (l-{l-a.)x/3H); (9)
Q°(x) ~qx(l-(i-a)x/2H). (10)
ЗЛО. Для зданий высотой не более 60 м расчетную эпюру ветровых нагрузок без большой погрешности можно принимать равномерно распределенной и равной (рис. 4, в):
q = const = 2М°(н)!нг) (11)
тогда усилия в любом уровне определяются зависимостями;
М°(х)-V,5qxz = М°(Н)хг/Нг; (12>
Q°(x) = 9* =2М°(Н)х/Нг. (13)
ЗЛ1. Значения момента М (Н) и поперечной силы Q вычисленные в соответствии с главой СНиП 11-6-74 "Нагрузки и воздействия", приведены в табл. 1 для условного грузового фронта, равного 1 м. При расчете зданий эти значения следует умножить на фактическую длину грузового фронта здания и на коэффициент, учитывающий i еографический район строительства (табл. 2)
ЗЛ2. Вертикальные нагрузки р приложены к отдельным столбам в общем случае внецентренно. Эксцентрицитеты, обусловленные неравномерностью загружения смежных пролетов или случайными погрешностями монтажа и вызывающие изгиб диафрагменных колонн и стенок из плоскости диафрагмы, учитываются при определении параметров несущей способности диафрагм.
8
|
Таблица 1 | ||||||||||||||||||||
|
Примечание. Ветровые нагрузки приведены для I района строительства (местность типа Б).
|
Таблица 2 | ||||||||||
|
Вертикальные нагрузки распределены по высоте здания равномерно.
В расчетах многоэтажных зданий следует учитывать понижающий коэффициент для временных нагрузок в соответствии с п. 3.9 главы СНиП П-6-74.
3.13. При нетиповых верхних этажах (зальные помещения и т.п.) возможны сосредоточенные нагрузки в уровне вер пршьузданкя в виде суммар
ных моментов Му , М* и горизонтальных сил 03 ,£)*. В этом случае сосредоточенные воздействия рекомендуется дополнительно учитывать при определении внешних усилий в сечении X . Возможны также и сосредоточенные вертикальные нагрузки Р * в каждом столбе, действующие в верхнем сечении с эксцентрицитетами f* * ,. е * .
4. АЛГОРИТМ СТАТИЧЕСКОГО РАСЧЕТА КАРКАСНО-ПАНЕЛЬНЫХ ЗДАНИЙ НА ОСНОВЕ ДИСКРЕТНО-КОНТИНУАЛЬНОЙ МОДЕЛИ
Дифференциальные уравнения и их модификация
4.1. В соответствии сп. 3.1 расчетная схема здания принимается в виде пространственной системы вертикальных стержневых элементов (столбов), соединенных непрерывно распределенными по высоте связями сдвига. Задача решается в системе прямоугольных координат, начало которых располагается в произвольной точке плана и совмещается по высоте с вершиной здания. Фрагменты расчетной схемы показаны на рис. 5.
4.2. Нагрузками на здание являются горизонтальные нагрузки Цы-^у(х) и
распределенные в общем случае по BbjcoTe здания по формулам (8) и (11), сосредоточенные моменты Му и М*, а также сосредоточенные поперечные силы G* и Q* (см. п. 3.13).
4.3. Кроме горизонтальных нагрузок рассматривается действие распределенных вертикальных нагрузок = р£ Ос), приложенных к отдельным столбам в общем случае с эксцентрицитетами е ус > е ri , а также сосредоточенных нагрузок Р* с эксцентрицитетами eyi , ez i -
4.4. В качестве неизвестных принимаются сдвигающие силы в связях 7} , поступательные перемещения vCy > в направлении одноименных осей и угол закручивания здания О . Все неизвестные представляют собой функ-ции вертикальной координаты * : г. - Т-(х), vQy = v (х)} *С2 - v0T (х),
6* ~ О '
9
2 Зак. 2001