Рекомендации по оптимальному проектированию железобетонных конструкций
Купить бумажный документ с голограммой и синими печатями. подробнее
Цена на этот документ пока неизвестна. Нажмите кнопку "Купить" и сделайте заказ, и мы пришлем вам цену.
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Рекомендации содержат принципиальные положения по оптимальному проектированию железобетонных конструкций, методы, алгоритмы и программы решения различных задач оптимального проектирования железобетонных конструкций как на ЭВМ, так и "вручную". В приложениях приведены вспомогательные материалы и примеры расчета. Рекомендации предназначены для инженеров—проектировщиков, специалистов вычислительных центров, научных сотрудников, занимающихся разработкой новых железобетонных конструкций и созданием систем их автоматизированного проектирования, а также для студентов строительных специальностей.
Оглавление
Предисловие
1. Общие указания
Основные положения
Основные определения
Тестовый пример оптимизации железобетонного изгибаемого элемента прямоугольного сечения
2. Общие принципы оптимального проектирования железобетонных конструкций
Целевая функция и переменные параметры
Выбор внешних и внутренних переменных параметров. Построение решений внешней и внутренней задач оптимизации железобетонных конструкций
Нормирование и округление внешних переменных параметров. Движение
Назначение начальных приближений
3. Алгоритмы решения внешней задачи оптимизации на основе теории планирования экстремальных экспериментов
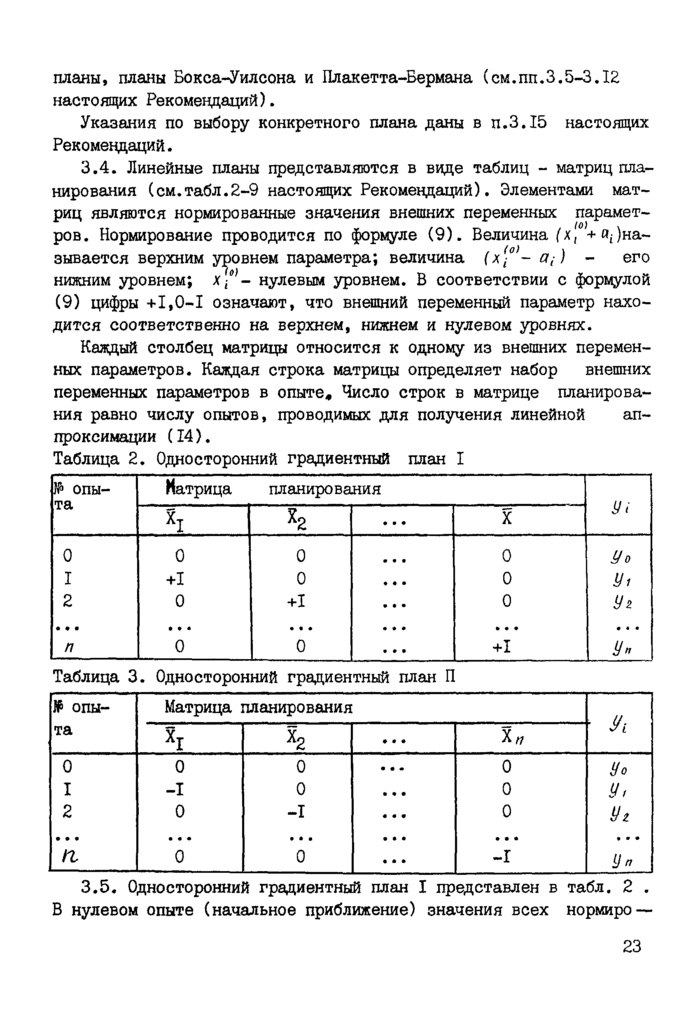
Основные положения
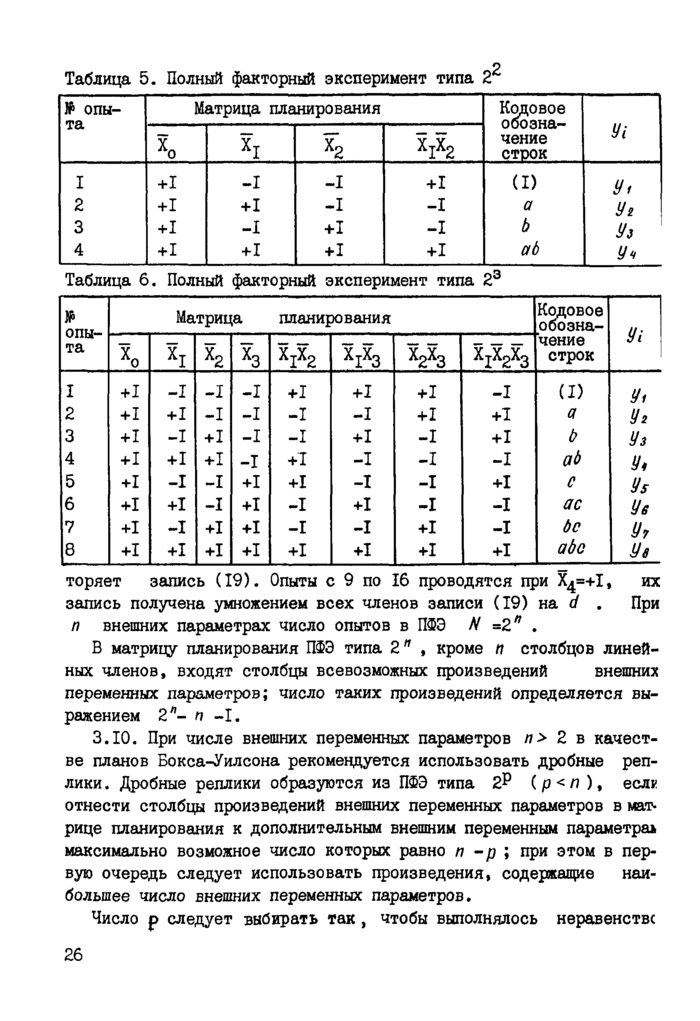
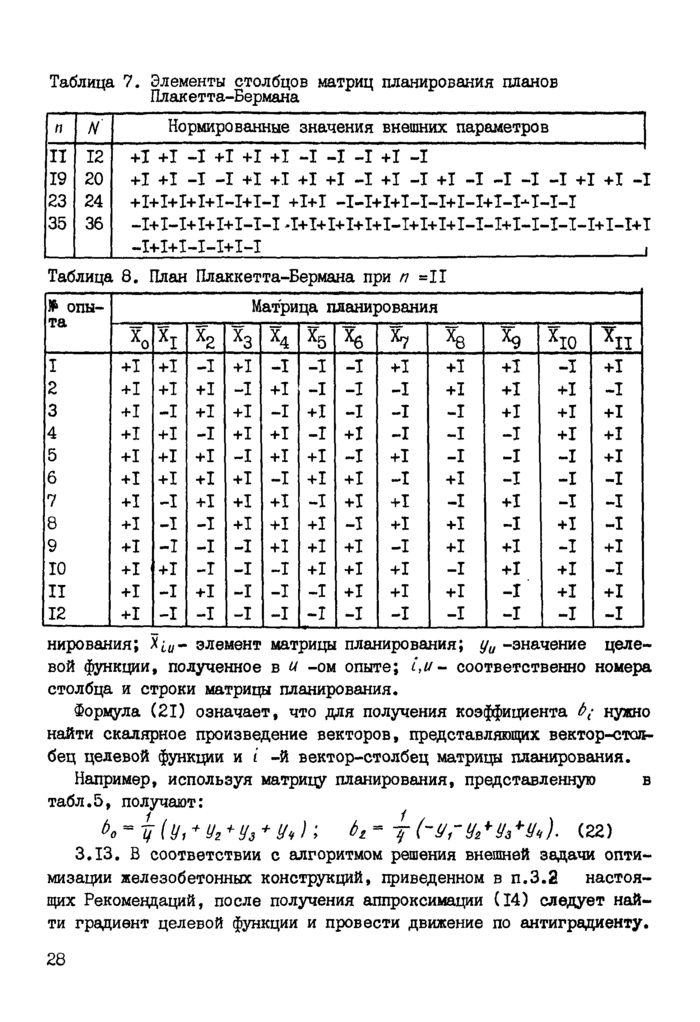
Линейные планы
Примеры расчета
4. Алгоритмы решения внешней задачи оптимизации на основе методов безусловной минимизации
Основные положения
Основные операции алгоритмов
Примеры расчета
5. Алгоритмы решения многоэкстремальных задач оптимального проектирования железобетонных конструкций
Основные положения
Основные операции алгоритмов
Примеры расчета
6. Решение многокритериальных задач оптимального проектирования железобетонных конструкций
Основные положения
Алгоритмы решения многокритериальных задач
Примеры расчета
7. Оптимальное проектирование номенклатур типовых железобетонных изделий
Основные положения
Методы решения задач
Примеры расчета
Приложение 1. Универсальные программы оптимизации. Оптимизация отдельных железобетонных конструкций и унифицированных серий
Приложение 2. Решение внутренней задачи оптимизации элемента, работающего на косое внецентренное сжатие
Приложение 3. Оптимизация предварительно напряженной двутавровой балки
Приложение 4. Оптимизация кольцевого фундамента под дымовую трубу
Приложение 5. Оптимизация вспарушенных плит
Приложение 6. Таблицы результатов опытов решения тестового примера оптимизации изгибаемого элемента прямоугольного сечения
Приложение 7. Таблица случайных чисел
Приложение 8. Основные принципы оптимизации железобетонных конструкций
| Дата введения | 01.01.2021 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот документ находится в:
- Раздел Строительство
- Раздел Экология
Организации:
| 13.09.1979 | Утвержден | НИИЖБ Госстроя СССР | |
|---|---|---|---|
| Разработан | НИИЖБ Госстроя СССР | ||
| Издан | НИИЖБ | 1981 г. |
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20

стр. 21

стр. 22
стр. 23

стр. 24

стр. 25
стр. 26

стр. 27
стр. 28

стр. 29

стр. 30
Н И И Ж Б ГОССТРОЯ СССР
РЕКОМЕНДАЦИИ ПО ОПТИМАЛЬНОМУ ПРОЕКТИРОВАНИЮ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
МОСКВА 1981
УДК 624.07.012.45
Печатаются по решению секции №1 бетонных и железобетонных конструкций НТО НИЖЕ Госстроя СССР от 13 сентября 1979 г.
Рекомендации по оптимальному проектированию железобетонных конструкций. М., НИИЖБ Госстроя СССР, 1981, 170 с.
Рекомендации содержат принципиальные положения по оптимальному проектированию железобетонных конструкций, методы, алгоритмы и программы решения различных задач оптимального проектирования железобетонных конструкций как на ЭВМ, так и "вручную". В приложениях приведены вспомогательные материалы и примеры расчета.
Рекомендации предназначены для инженеров-проектировщиков, специалистов вычислительных центров, научных сотрудников, занимающихся разработкой новых железобетонных конструкций и созданием систем их автоматизированного проектирования, а также для студентов строительных специальностей.
©
Табл. 62 , илл. 9
Научно-исследовательский институт бетона и железобетона Госстроя СССР, 1981
| ||||||||||||||||||
|
а!3 |
У/
У 2
»----- 4
•fc—»—1'
|
Е- —д | ||
|
У4 | ||
|
Е—4—Я | ||
|
К-1 |
—1 | ||
|
W5 | |||
|
1-1 • I • л |
> | ||
|
У 6 | ||||||||||||
|
РисЛ. Схемы армирования изгибаемого элемента прямоугольного поперечного сечения в тестовом примере
Локальные минимумы у (х,,хг,.^оказались следующими: </(10,45,300) = 3,24 руб., </( 10,50,400)=3,27 руб., у (ТО,55,250)=3,14 руб.{гло
бальный минимум у (10,55,250)=3,14 руб.
2. ОБЩИЕ ПРИНЦИПЫ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ Целевая функция и переменные параметры
2.1. Выбор целевой функции следует проводить с учетом конкретных целей проектирования железобетонных конструкций. Как правило, целевой функцией рекомендуется принимать приведенные затраты. Допускается использовать любую другую целевую функцию - суммарную стоимость материалов в деле, расчетную производственную себестои-
II
мость, оптовую цену, расход арматуры и т.п. Допускается также использовать векторную целевую функцию, состоящую из любого числа скалярных. Скалярными целевыми функциями рекомендуется принимать стоимость, расходы бетона и металла, трудоемкость и пр.
2.2. Для определения значений целевой функции при фиксированных значениях внешних и внутренних переменных параметров реко -мендуется пользоваться Руководствами по определению расчетной стоимости и трудоемкости изготовления сборных железобетонных конструкций на стадии проектирования. Конструкции жилых и общественных зданий (К., 1977) и Конструкции промышленных зданий (М., 1976) и Руководством по определению стоимости эксплуатации промышленных зданий и сооружений на стадии проектирования (М., 1977), Нормами расхода материалов и изделий на 1000 м^ приведенной общей площади жилых зданий (И., 1978), Прейскурантом № 06-08 оптовых цен на железобетонные изделия (Ы., 1974) и другими инструктивными и нормативными документами.
2.3. Переменными параметрами при оптимизации железобетонных конструкций рекомендуется назначать общие геометрические размеры конструкций и геометрические размеры отдельных элементов, марку бетона, класс стали, площади сечений арматуры (обычной и преднапрякенной, растянутой и сжатой, продольной и поперечной ), величину натяжения преднапрягаемой арматуры, число арматурных стержней, количество каркасов и т.п.
2.4. При оптимизации железобетонных конструкций переменные параметры, как правило, следует считать дискретными. В отдельных случаях допускается переменные параметры считать непрерывными.
Например, иногда в расчетах отвлекаются от существующих сортаментов арматурной стали и используют полученные в результате вычислений площади сечения арматуры; если расчет выполняется в исследовательских целях, в нем могут быть использованы реальные характеристики материалов и т.п.
2.5. Если для оптимизируемой железобетонной конструкции определяющими являются условия прочности, оптимальный по стоимости класс рабочей арматуры следует выбрать заранее. С этой целью необходимо :
а) для всех классов арматуры, которые могут найти применение в конструкции, определить площадь сечения арматуры, воспринимающую одну и ту же растягивающую силу;
б) .вычислить стоимость арматуры длиной I м с найденной пло-
щадью сечения;
в) в качестве оптимального выбрать тот класс, для которого полученная стоимость минимальна.
Выбор внешних и внутренних переменных параметров.
Построение решении внешней и внутренней задач оптимизации железооетонных'конструкций
2.6. Выбор внешних и внутренних параметров следует проводить с учетом ранее разработанных методов решения внутренней задачи оптимизации. В пп.2.7-2.9 настоящих Рекомендаций приводятся три характерных случая решения внутренней задачи оптимизации и выбора внутренних переменных параметров.
2.7. Пв£вый_случай. Метод расчета конструкции известен; по определенным в результате расчета внутренним усилиям минимальные площади сечезшя арматуры, при которых удовлетворяются необходимые ограничения, определяются непосредственно согласно главе СНиП по проектированию железобетонных конструкций. При этом согласно главе СНиП П-21-75 определяются также: защитный слой бетона, количество арматурных каркасов и арматурных стержней (продольных и поперечных), расстояния между стержнями и т.п. Все перечисленные параметры, определяемые непосредственно согласно главе СНиП П-21-75 рекомевдуется принимать внутренними. Внутреннюю задачу оптимизации рекомендуется решать согласно главе СНиП П-21-75.
Например, при оптимизации железобетонного изгибаемого элемента, рассмотренного в тестовом примере (см.п.1.7 настоящих Рекомендаций), внутреннюю задачу оптимизации решали согласно главе СНиП по проектированию железобетонных конструкций, определяя минимальную площадь сечения арматуры, удовлетворяющую условию прочности.
2.8. Второй_случай. Метод расчета конструкции известен, но по определенным в результате расчета внутренним усилиям минимальную площадь сечения арматуры, при которой удовлетворяются необходимые ограничения, непосредственно согласно главе СНиП П-21-75 подобрать нельзя: для действующих усилий существует только поверочный расчет.
Здесь внутренние переменные параметры рекомендуется выбирать такими же, капе в первом случае. Внутреннюю задачу оптимизации рекомендуется решать согласно главе СНиП П-21-75 в сочетании с од-ним из методов одномерного поиска *
* Методы одномерного поиска изложены, например, в книге Д.Уайлда "Методы поиска оптимума" (М., 1967;.
13
Один из методов одномерного поиска - метод деления отрезка пополам - изложен в прил. 2 настоящих Рекомендаций.
Например, пусть требуется оптимизировать железобетонное прямоугольное сечение, работающее на косое внецентренное сжатие при фиксированной величине действующих усилий. Минимальное из условий прочности армирование при заданных геометрических размерах сечения и характеристиках материалов определяется следующим образом. Задают все возможные варианты армирования и располагают их в порядке возрастания несущей способности. В соответствии с процедурой какого-либо из методов одномерного поиска назначают один из возможных вариантов и проверяют его несущую способность по СНиП. Если несущая способность оказывается меньше требуемой , принимают следующий вариант с большим армированием; если несущая способность больше требуемой - вариант с меньшим армированием. Процесс повторяют до тех пор, пока при одном значении площади сечения арматуры несущая способность больше требуемой, а при другом ближайшем возможном значении, меньшем предыдущего, несущая способность недостаточна. Это предыдущее значение и определяет вариант с минимальным армированием.
Числовой пример, иллюстрирующий рассматриваемый случай, приведен в прил.2 настоящих Рекомендаций.
2.9. Третий_случай. Известен метод оптимизации конструкции по некоторым параметрам. Остальные параметры, которые можно было бы варьировать в процессе оптимизации, остаются фиксированными. Принцип разделения параметров позволяет принять все параметры переменными, разделив их на внутренние и внешние. Внутренними рекомендуется выбирать параметры, служившие переменными в разработанном методе оптимизации; внешними - ранее фиксированные параметры. Внутреннюю задачу рекомендуется решать с использованием разработанного метода оптимизации. Внешние переменные параметры в каждом опыте фиксируют в соответствии с процедурой решения внешней задачи оптимизации.
Примечание. Например, С.М.Крыловым и др.к разработан метод оптимального армирования железобетонных рам. Переменными параметрами при решении задачи были площади поперечных сечений и места расположения ар-
й Крылов С.М. и др. Оптимальное армирование статически неопределимых железобетонных рам с учетом требований трех предельных состояний - В кн.: Теория железобетона. М., 1972.
матурных стержней, марка бетона, класс стали. Геометрические размеры сечений прямоугольных элементов рам фиксировали. Для решения задачи применяли линейное программирование.
Принцип разделения параметров позволяет расширить и обобщить разработанный метод оптимального армирования, поставив задачу оптимального проектирования железобетонных рам по стоимости. Внутренними переменными параметрами рекомендуется принять площади поперечных сечений и места расположения арматурных стержней, марку' бетона, класс стали; внешними - геометрические размеры сечений элементов стали. В каждом опыте геометрические размеры сечений элементов фиксируют и решают внутреннюю задачу оптимизации с использованием линейного программирования, определяя оптимальные значения внутренних переменных параметров. Зная удельные стоимости материалов, находят общую стоимость конструкции. В результате решения, внешней задачи оптимизации определяют рану минимальной стоимости.
Аналогичный числовой пример приведен в прил. 4 настоящих Рекомендаций.
2.10. Решение внутренней задачи оптимизации должно учитывать,
если необходимо, множество нагружений конструкции. Учет многих загружений при решении внутренней задачи оптимизацию рекомендуется проводить так же, как и при обычном проектировании: каждый
опыт представляет собой вариант проектирования конструкции.
Пусть, например, расчет конструкции выполняется в упругой стадии, а подбор сечений арматуры (внутренних переменных параметров) проводится согласно главе СНиП П-21-75. Тогда выполняют расчет на каждое загружение. Затем выбирают невыгодные сочетания нагрузок и подбирают минимальные площади сечения арматуры при действии каждого сочетания. Окончательно принимают максимальную из полученных площадей. Такую процедуру повторяют в каждом опыте.
2.11. Решение внутренней задачи оптимизации должно учитывать требования всех предельных состояний. При этом одно из состояний рекомендуется считать основным, а другие - дополнительными. В процессе решения внутренней задачи оптимизации вначале удовлетворяют требованиям основного состояния так, чтобы целевая функция имела минимальное значение. Для удовлетворения требованиям других предельных состояний применяют пороговую оптимизацию: проводя оптимизацию по основному предельному состоянию, требуют, чтобы одновременно выполнялись требования дополнительных предельных состояний.
15
Пусть, например, как и в примере п.2.10 настоящих Рекомендаций, расчет конструкции выполняется в упругой стадии, а подбор сечений арматуры проводится согласно главе СНиП П-21-75. Основным предельным состоянием можно выбрать прочность; дополнительными - жесткость и ширину раскрытия трещин. Подбирая сечение арматуры, удовлетворяют требованиям основного предельного состояния. Если при этом деформации или ширина раскрытия трещин больше допустимых, сечение арматуры увеличивают. Пытаются добиться выполнения требований дополнительных предельных состояний при минимальном расходе арматуры.
2.12. Внешнюю задачу оптимизации рекомендуется решать проведением ряда опытов. Фиксированные наборы значений внешних переменных параметров в опытах рекомендуется задавать согласно алгоритмам, приведенным в разделах 3-6 настоящих Рекомендаций.
При фиксированных наборах значений внешних переменных параметров выполнение внешних ограничений (3) рекомендуется просто проверять. Если в каком-либо опыте внешние ограничения (3) не выполняются, это рекомендуется учитывать одним из следующих способов :
1) на целевую функцию накладывается штраф - ее значение в опыте увеличивается по определенный правилам;
2) принятый с целью уменьшения целевой функции порццок изменения внешних переменных параметров отменяется и отыскивается новый порядок их изменения.
2.13. При решении внутренней задачи оптимизации может оказаться, что в каком-либо из опытов не существует значений внутренних переменных параметров, удовлетворяющих внутренним ограничениям (5), т.е. внутренняя задача оптимизации решения не имеет. В этом случае рекомендуется поступать так же, как и в случае , когда в опыте не выполняются внешние ограничения (см.п.2.12 настоящих Рекомендаций).
2.14. В общем случае при разделении переменных параметров на внутренние и внешние должны выполняться следующие требования.
1) внешние и внутренние переменные параметры должны делить ограничения на две группы - внешние ограничения, содержащие только внешние переменные параметры, и внутренние ограничения, содержащие как внешние, так и внутренние переменные параметры;
2) в большинстве опытов должны существовать значения внутренних переменных параметров, при которых выполняются все внутрен-
16
ние ограничения, т.е. должна иметь решение внутренняя задача оптимизации;
3) большая часть ограничений на конструкцию должна быть отнесена к внутренним ограничениям; внешние ограничения должны быть слабыми: чем слабее внешние ограничения, тем успешнее осуществляется оптимизация на основе принципа разделения параметров. Наилучшим является случай, когда внешние ограничения сводятся к виду (4);
4) внутренними переменными параметрами следует назначать минимальное число параметров, удовлетворяющим требованиям 1-3; остальные параметры принимаются внешними.
Как правило, внутренними параметрами рекомендуется принимать параметры, связанные с армированием - площади сечений арматуры (растянутой и сжатой, обычной и предварительно напряженной, продольной и поперечной), величину натяжения преднапрягаемой арматуры, число арматурных каркасов, расстояния между арматурными стержнями, защитный слой бетона, геометрические размеры, связанные с размещением арматуры и т.п. Внешними переменными параметрами, как правило, рекомендуется назначать общие геометрические размеры конструкции, геометрические размеры отдельных ее элементов, характеристики материалов.
Нормирование и округление внешних переменных параметров.
Движение
3.15. Для некоторых алгоритмов решения внешней задачи оптимизации (см.разделы 3-6 настоящих Рекомендаций) внешние переменные параметры рекомендуется приводить к безразмерному виду, или нормировать. Для нормирования внешних переменных параметров назначают точку х(0* = (х1°\... х^1) ,р которую помещают начало координат. Эта точка должна удовлетворять двум условиям:
1) в ней выполняются внешние ограничения (3);
2) внутренняя задача оптимизации в этой точке имеет решение.
Нормированное значение внешнего параметра определяют по
Ф°Р“Уле X,- = ( хi - Х(?')]сч , (9)
где X i - некоторое размерное значение L -го переменного параметра.
Величину ai в формуле (9) принимают на основании следующих соображений. Если шаг изменения внешнего переменного параметра х i сохраняется постоянным, то величину a-L принимают равной
17
этому шагу. Шаг изменения переменного параметра может быть разным. Пусть внешний параметр *,■ имеет р разных шагов а^. Тогда допускается использовать два способа нормирования этого внешнего параметра, принимая в формуле (9):
I) ас = max aip) и 2) - min (at1.....alp).
При неравномерном шаге возможен также третий способ нормирования: все значения х} считает равноудаленными друг от друга, расстояния между ними принимают равными любому целому числу ( чаще всего единице).
2.16. Иногда дискретные значения внешнего переменного пара» метра задают некоторыми символами, не имеющими физического смысла. Тогда размерным значением параметра рекомендуется принимать какую-либо характерную величину, имеющую физический смысл. Например, различные классы арматуры обозначают символами A-I, Ат-У1 и т.п. Характерной величиной, задающей размерные значения внешнего переменного параметра, принимают расчетное сопротивление арматуры Ra, которое используют в формуле (9).
2.17. Дискретность внешних переменных параметров в алгоритмах решения внешней задачи оптимизации рекомендуется учитывать округлением непрерывных значений до ближайших дискретных. С этой целью вводят операцию округления.
Пусть из п внешних параметров г переменных параметров дг<-непрерывны, a in-r) переменных параметров ^(/=^7,..,^дискретны . Пусть некоторые значения внешних переменных параметров х1г...,х„ получены без учета дискретности (п-г) параметров. Пусть ближайшие дискретные значения (л -г) параметров равны х* (I* г+1,.„,п). Операцию округления обозначают Ок и записывают так:
Бели округление* провЪдится по всем внешним переменным параметрам, это записывают так:
Ох (х,.....х„) = (х*,...,Х*), или 0к(х)~(х*), (И)
Опыты проводят при значениях внешних параметров, получаемых в результате округления.
2.18. При разработке алгоритмов решения внешней задачи оптимизации рекомендуется пользоваться понятием движения.
Для движения необходимо иметь систецу координат и определить в ней направляющий вектор, задающий прямую. Совершить движение -это значит найти точку на прямой (если все внешние переменные
параметры непрерывны) иди точку, ближайшую к пряной (если среди внешних переменных параметров есть дискретные), так, чтобы в этой точке выполнялись все ограничения и целевая функция имела минимальное значение по сравнению соответственно с точками н а прямой иди точками, ближайшими к прямой. Точка (X,,..., х„ ) считается ближайшей к прямой , если на прямой существует такая точ-ка ( хп ), что Ок (х1г..., х„ ) = (х,,...,х„)\ при этом предполагается, что округление осуществляется по всем дискретным параметрам.
2.19. Для выполнения движения рекомендуется использовать процедуру, состоящую в последовательном задании точек, ближайших к направлению движения. В п.2.20 настоящих Рекомендаций эта процедура описана для случал, когда все внешние переменные параметры дискретны. Случай, когда среди внешних переменных параметров есть непрерывные, рассмотрен в п.3.13 настоящих Рекомендаций.
Для выполнения движения допускается использовать различные процедуры одномерного поиска в сочетании с округлением, проводимым по формулам (10), (II).
2.20. Для выполнения процедуры движения, состоящей в последовательном задании точек, ближайших к направлению движения, следует принять:
S = (5,, S п) - направляющий вектор;
х(°> = (х (/’...,хгп0>) - точку начала движения, через которую проходит направляющий вектор.
Чтобы провести движение, представляют вектор в несколько ином виде. Находят такое г , что Sz = max/Sil . Определяют век-
тор 1 ; to
В векторе I mgx lit I = \lz\ =1. Задача движения состоит в отыскании точки х , в которой удовлетворяются внутренние и внешние ограничения и выполняется условие:
у(х111)- min у Г0к(Х(о) + Aj I)]. (13)
Для решения задачи рассматривают ряд последовательных соседних дискретных значений нормированного внешнего переменного параметра Xzj (j ■= 0, 1, 2,...) в направлении, определяемом знаком координаты lz вектора I (если координата 4 положительна, т о Л to <xt1 < Хг2<.„); значение xzo совпадает с координатой ? (°> точки X /0>. Затем задают значения Я; по формуле
^j~XZj—XtQf J™0,1,2,...
19
Тогда выражение у (Xм +Х1) даст все точки, ближайщие к лучу с началом в точке х !о> ; направление луча определяется вектором I . Чтобы найти точку х'° по формуле (13), достаточно вычислять выражение y=y[OK(x0 + Xjl) при j =0,1,2,... до тех пор, пока выполняются внутренние и внешние ограничения и целевая функция
уменьшается. В этом состоит процедура движения в направлении вектора S .
В процессе движения один или несколько внешних переменных параметров могут принять граничные значения du или diz из (4) .
Пусть t < п параметров хXf приняли граничные значения
(этого можно добиться изменением нумерации параметров). При движении фиксируют эти параметры, приравняв их значения граничным . Продолжают движение, считая S = (5tf1S„). Совершают движение, если целевая функция уменьшается и выполняются внутренние и внешние ограничения (3), (5). В противном случае движение прекращают. Движение также прекращают, если t - п .
В формуле (13) под вектором I понимают как вектор, определяемый по формуле (12), так и "укороченный" вектор / = (/„). Переход от вектора S = (Stf1,Sn) к вектору / * t„)
осуществляют по формуле (12).
Назначение начальных приближений
2.21. При оптимизации железобетонных конструкций в качестве начальных приближений рекомендуется принимать наилучшие известные решения, удовлетворяющие необходимым ограничениям. Такие решения рекомендуется принимать, используя имеющиеся аналоги, инженерный опыт и интуицию. Приведенные ниже рекомендации по назначению начальных приближений обобщают опыт оптимизации некоторых конструкций.
I. В двутавровых и тавровых сечениях элементов конструкций, работающих на изгиб, ширину и толщину полок рекомендуется назначать минимальными. В двутавровых сечениях рекомендуется назначать минимальной также толщину стенки. В прямоугольных и тавровых сечениях толщина стенки также должна быть минимальной, но с учетом расположения растянутой арматуры:следует иметь в виду, что при очень малой ширине, когда растянутую арматуру приходится располагать в несколько радов по высоте, плечо внутренней пары уменьшается, вследствие чего расход арматуры и стоимость увеличиваются. Высоту сечений рекомендуется, как правило, назначать в
20
ПРЕДИСЛОВИЕ
Настоящие Рекомендации содержат основные положения по оптимально^ проектированию железобетонных конструкций и предназначены для улучшения их технико-экономических показателей - снижения массы, металлоемкости, стоимости и т.п.
В Рекомендациях приведены алгоритмы и описаны программы для ЭВМ, которые пригодны для оптимизации 1 любых железобетонных конструкций или железобетонных конструкций определенного класса. Наиболее типичные случаи иллюстрируются числовыми примерами.
Читателю, впервые знакомящемуся с вопросами оптимизации железобетонных конструкций, изучение материалов, изложенных в Рекомендациях, следует начинать с приложения 81 которое является как бы "ключом" к основному тексту. В этом приложении приведены основные понятия, постановки и способы решения простейших задач, чаще всего возникающих в практике проектирования. Показано, как предлагаемые подходы развиваются для решения более общих задач оптимизации железобетонных конструкций.
Настоящие Рекомеедации разработаны НИИЖБ Госстроя СССР (канд. техн. наук М.Б.Краковский) при участии ряда научно-исследовательских организаций на основе результатов научно-исследовательских работ а также накопленного за последние годы опыта оптимизация железобетонных, в той числе тонкостенных пространственных конструкций.
Отдельные приложения настоящих Рекомендаций составили:
приложение I - универсальные программы оптимизации-канд.техн. наук В.Н.Уколов (ЩИПИАСС Госстроя СССР) программа оптимизации железобетонных стержневых конструкций - канд.техн.наук В.Т.Алек-сандров и инж. С. А .Перевозов (Ленпромстройпроект Госстроя СССР); программа оптимизации ребристых железобетонных плит - кандидаты техн. наук М.А.Янкелевич и Я.И.Маркус (НИИСК Госстроя СССР); программа оптимального армирования круглых плит и кольцевых фундаментов - д-р техн. наук, проф. В.И. Соломин и инж. С.Б.Шматков (Челябинский ПИ Минвуза РСФСР); рекомеедации по выбору оптималь-
пределах I/I0-I/20 пролета. Марку бетона для конструкций без предварительного напряжения арматуры рекомендуется назначать в пределах 250-350, а для предварительно-напряженных конструкций - в пределах 400-500.
2. Сечения внецентренно сжатых элементов конструкций с очень малыми эксцентрицитетами рекомендуется в начальном приближении проектировать близкими к квадратным, а марку бетона назначать максимальной. Геометрические размеры таких сечений при заданной марке бетона рекомендуется назначать максимальными, чтобы несущая способность элемента минимально отличалась от заданной при минимальном армировании. Чем больше эксцентрицитет, тем больше должно быть соотношение между высотой прямоугольного сечения и его шириной; при увеличении эксцентрицитета рекомендуется также снижать марку бетона. В пределе при действии только изгибающего момента без нормальной силы сечения задаются по рекомендациям п.1.
3. Из условий прочности целесообразно повышать класс стали рабочей арматуры. В конструкциях с ненапрягаемой арматурой, если определяющими являются требования ограничения по ширине раскрытия трещин, класс стали рабочей арматуры иногда целесообразно понижать.
4. Толщину поля ребристых плит - сборных и монолитных, плос— ких и криволинейных - следует назначать минимально возможной.
5. В фундаментах марку бетона следует назначать в пределах 200-300. Геометрические размеры фундаментов, как правило, определяются несущей способностью по грунту и расчетом на продавли-вание.
6. Жесткости стержней плоских рам, работающих на одновременное действие статических и сейсмических нагрузок, следует назначать минимально возможными.
7. В пологих оболочках положительной гауссовой кривизны стрелы подъема в центре и на контуре следует назначать максимальными.
Положения п.2.21 позволяют приблизить начальные приближения к оптимальным по стоимости решениям и тем самым сократить процесс оптимизации.
21
ных параметров железобетонных висячих оболочек - кандидаты техн. наук М.А.Иванов (НИИЖБ Госстроя СССР) и Т.А.Усачев (ЦНИИЭП торгово-бытовых зданий и туристских комплексов Гоогражданотроя при Госстрое СССР); рекомендации по выбору оптимальных параметров железобетонных куполов - кандидаты техн. наук Н.В.Ахвледиани и
М.А.Даниелашвили (ИСМиС АН ГрузССР); программа решения однопараметрических задач оптимального проектирования номенклатур типовых конструкций - канд.техн. наук М.А.Янкелевич (НИИСК Госстроя СССР); программа решения многопараметрической задачи оптимального проектирования номенклатур типовых конструкций - Г.Г.Джаникян (ЦНИИПромзданий Госстроя СССР);
приложение 5 - канд.техн. наук Б.Н.Бастатский, инж е н еры М.А.Адамова и Н.Г.Барабадзе (ГрузНИИЭГС Минэнерго СССР).
Общее составление и редактирование Рекомендаций осуществлено канд.техн. наук М.Б.Краковским.
Замечания и предложения по содержанию Рекомендаций просим направлять в НИИЖБ по адресу: 109389, Москва, 2-я Институтская ул., д.б.
Дирекция НИИЖБ
4
I. ОБЩИЕ УКАЗАНИЯ Основные положения
1.1. Настоящие Рекомендации распространяются на оптимизацию железобетонных конструкций, рассчитываемых и конструируемых согласно главе СНиП П-21-75 "Бетонные и железобетонные конструкции"
1.2. При оптимизации железобетонных конструкций специальных видов (фундаментов, оболочек, складок и т.п.), а также конструкций, работающих в особых условиях (в районах с сейсмичностью 7 баллов и более, на просадочных грунтах и подрабатываемых территориях, в условиях воздействия повышенных и высоких температур и т.п.) их расчет и конструирование следует проводить согласно специальным указаниям.
1.3. Настоящие Рекомендации содержат методы и алгоритмы решения различных задач оптимизации железобетонных конструкций. При описании алгоритмов они представляются состоящими из трех этапов: А - начало работы, Б - К-ый шаг; В - конец работы.
Работа алгоритмов иллюстрируется на тестовом примере оптимизации изгибаемого железобетонного элемента. Условия тестового примера описаны в п.1.7 настоящих Рекомендаций.
Примеры оптимизации различных железобетонных конструкций приведены в прил. 1-5 настоящих Рекомендаций.
Основные определения
1.4. При оптимизации железобетонных конструкций используются следующие понятия и термины.
1) Целевая функция - критерий качества, по которому проводится оптимизация конструкции. В качестве целевой функции могут быть выбраны расчетная производственная себестоимость, оптовая цена, расход металла и пр. При выборе целевой функции следует руководствоваться указаниями пп.2.1-2.2 настоящих Рекомендаций.
2) Скалярная целевая функция - целевая функция, состоящая из одного критерия качества, например, стоимости.
Скалярная целевая функция обозначается у .
3) Векторная целевая функция - целевая функция, состоящая из нескольких критериев качества, например, стоимости, трудоемкости, расхода металла, расхода бетона.
Векторная целевая функция обозначается У ~ (Уи---Уе)
5
где уур - р скалярных целевых функций, образующих векторную.
4) Переменные параметры - параметры конструкции, которые могут в процессе оптимизации принимать различные значения. В качестве переменных параметров могут быть выбраны геометрические размеры конструкции или отдельных ее элементов, характеристики материалов, площади сечения арматуры и пр. При выборе переменных параметров следует руководствоваться указаниями пл.2.3-2.5 настоящих Рекомендаций.
Переменные параметры обозначаются к 1х1 .
5) Ограничения - записываемые в виде равенств и неравенств требования, предъявляемые к конструкции. Ограничениями могут быть требования прочности, жесткости, трещиностойкости, технологичности и т.п.
6) Задача оптимизации конструкций - задача выбора такого значения переменных параметров, при которых достигает минимума целевая функция и выполняются необходимые ограничения.
Задача оптимизации железобетонных конструкций записывается в следующем виде.
Найти min у (xty...,x() U1
при выполнении ограничений
Ji ( X , ... xL ) * 0 ; i = 1, ...L , (2)
где Ji - функции ограничений; L - общее число ограничений.
При необходимости вместо задачи минимизации решать задачу максимизации рекомендуется вместо целевой функции у рассматривать целевую функцию у-' =-у .
7) Однокритериальная задача оптимизации - задача минимизации скалярной целевой функции при выполнении необходимых ограничений.
8) Многокритериальная задача оптимизации - задача минимизации векторной целевой функции при выполнении необходимых ограничений.
9) Одноэкстремальная задача оптимизации - задача оптимизации при единственном минимуме целевой функции.
10) Многоэкстремальная задача оптимизации - задача оптимизации при нескольких минимумах целевой функции. Минимальный из минимумов - глобальный минимум; остальные минимумы - локальные.
11) Внешние переменные параметры - переменные параметры, задаваемые независимо от других переменных параметров. Внешними переменными параметрами могут быть, например, выбраны геометрические размеры конструкции или отдельных ее элементов, характеристики материалов и пр. Внешние переменные параметры следует
б
выбирать в соответствии с указаниями пп.2.6-2.9 настоящих Рекомендаций. Внешние переменные параметры обозначаются хj,...,x„ (п<1)
12) Внутренние переменные параметры - переменные параметры, определяемые в зависимости от значений внешних переменных параметров. Внутренними переменными параметрами могут быть выбраны , например, площади сечений арматуры, количество арматурных каркасов, количество арматурных стержней, расстояния между стержнями и пр. Внутренние переменные параметры следует выбирать в соответствии с указаниями пп.2.6-2.9 настоящих Рекомендаций. Внутренние переменные параметры обозначаются х„+,хг , их число равно т = / - п .
13) Внешние ограничения - ограничения, в которые входят только внешние переменные параметры. Внешние ограничения записываются в следующем виде:
Ji i = 1,... N, (3)
где N - общее ^исло внешних ограничений.
Частным случаем внешних ограничений являются органичения ви-
Д d^ Xj ^ d2l ; i — 1n , (4)
где c/lL и d2i - соответственно минимальное и максимальное возможные значения внешнего переменного параметра X; .
14) Внутренние ограничения - ограничения, в которые входят как внешние, так и внутренние переменные параметры (или только внутренние). Внутренние ограничения записываются в следующем ви-
Де: У/ xt)*0 + (5)
где L -N=M- общее число внутренних ограничений.
15) Внутренняя задача оптимизации - задача определения оптимального значения внутренних переменных параметров хя+/х{ , при которых выполняются внутренние ограничения (5) и достигает минимального значения целевая функция; внешние переменные параметры при этом фиксируются. Внутренняя задача оптимизации записывается в следующем виде.
Найти min ,д,
при выполнении неравенств (5) и заданных значениях Х„ .
16) Внешняя задача оптимизации - задача определения такого значения внешних переменных параметров х,,..., хп , при котором выполняются внешние ограничения и из всех возможных решений внут-
7
ренних задач оптимизации выбирается решение с минимальным значением целевой функции. Внешняя задача оптимизации записывается в следующем виде.
Найти min min у ( х,х, )
при выполнении неравенств (3).
17) Опыт - совокупность следующих операций: фиксирование значений внешних переменных параметров; проверка выполнения внешних ограничений (если внешние ограничения не выполняются, проведение опыта прекращается); решение внутренней задачи оптимизации; вычисление значения целевой функции.
18) Вектор, или точка х - набор значений внешних переменных
параметров X = (х1>...,хп), Точка обозначается также; x(j> = (x^t[.,Xlnj)J t или — (x/1*'{!..,X^j>), где j - номер точки; К - номер шага
алгоритма.
Нижний индекс обозначает номер внешнего переменного параметра. Точка начала координат обозначается хt0> = (х ,/aJ,, xj?1).
T9) Глобальная система координат - система координат, при которой начало координат х 101 остается в одной и той же точке в процессе решения внешней задачи оптимизации.
20) Локальные системы координат - системы координат, при ко-
(01
торых начало координат х находится в различных точках в процессе решения внешней оптимизации.
21) Точка х /г> называется более предпочтительной по сравнению
(7 }
с точкой х , если для векторного критерия выполняется неравенство У(Хщ « т.е. среди неравенств y1 (х(t>) « yt(x(li);...;
Ур(х(1>)<* ур (х/г>) найдется хотя бы одно строгое. Если же У(х°^-у(х(г)), т.е. у,(х(11)=у,(х/£>);ур (x<i}) = ур (х<г’) , то точки х"> и х1^называются эквивалентными.
22) Множество точек, для которых не существует более предпочтительных, называется множеством Парето. В точках множества Парето должны выполняться внешние и внутренние ограничения (3),(5). Множество Парето обозначается буквой П.
1.5. Оптимизацию железобетонных конструкций рекомендуется выполнять на основе принципа разделения параметров. Основные положения принципа состоят в следующем:
1) все переменные параметры делятся на две группы; параметры одной группы называются внутренними, другой - внешними.
2) общая задача оптимизации (I), (2), делится на две подзада-
чи - внутреннюю (6) и внешнюю (7);
3) решение внутренней задачи оптимизации строится с использованием ранее разработанных расчетов железобетонных конструкций или методов их оптимизации по части параметров;
4) решение внешней задачи оптимизации строится с помощью алгоритмов, основанных на методах теории планирования экстремальных экспериментов, безусловной минимизации и случайного поиска.
Тестовый пример оптимизации железобетонного изгибаемого элемента прямоугольного сечения
1.6. В п.Х.7 настоящих Рекомендаций приведено описание условий тестового примера оптимизации железобетонного изгибаемого элемента прямоугольного сечения. Указанный тестовый пример позволяет продемонстрировать работу алгоритмов, изложенных в раэд.3-7, а также иллюстрирует основные определения, перечисленные впп.1.4-1.5 настоящих Рекомендаций.
1.7. Рассматривается задача оптимального проектирования железобетонного элемента прямоугольного поперечного сечения, на который действует постоянный по величине изгибающий момент М=85кНм
Внешними переменными параметрами выбираются х, - ширина сечения (Ь ); х2 - его высота (h ); х3 - марка бетона (Rg). Арматура принимается из стали класса А-П; класс стали не варьируется. Расстояние до центра тяжести сжатой арматуры а ' принимается постоянным и равным 3,5 см. Внутренними переменными параметрами выбираются: количество и диаметр арматурных стержней растянутой и сжатой арматуры, определяющих площади F& и Ра; количество арматурных каркасов; расстояние до центра тяжести растянутой арматуры; расстояние между стержнями.
Внутренними ограничениями служат требования обеспечения прочности нормального сечения элемента. Внутренняя задача оптимизации состоит в определении минимальных площадей арматуры Ра и Ра, обеспечивающих прочность сечения. При каждом фиксированном наборе внешних переменных параметров эта задача решается согласно главе СНиП П-21-75.
В прил.б приведены результаты 960 опытов, выполненных при всех возможных комбинациях следующих дискретных значений внешних переменных параметров:
Хт i Ь ) - 10,12,14,15,16,18,20,22,24,25 см;
Х2 {h ) _ 25,30,35,40,45,50,55,60,65,70,75,80 см;
9
Х3 (R6) - 150,200,250,300,350,400,450,500.
Таким образом, единственными внешними ограничениями являются неравенства типа (4):
ТО см^Х^^25 см; 25 cM^Xg^BO см; I50^Xg<500. (8)
Значение целевой функции у в каждом опыте определяется как сумма стоимостей в деле материалов (бетона и арматуры) при длине элемента, равной I м. Удельная стоимость арматуры принята равной 1020 руб/м3, удельные стоимости бетонов различных марок приведены в табл Л.
Каждый опыт проводится в следующем порядке:
Т. Задают значения внешних переменных параметров.
2. Согласно главе СНиП II-2I-75 определяют минимальные теоретические площади сечения растянутой и сжатой арматуры, обеспечивающие прочность сечения. При этом принимают, что а = я =3,5 см.
3. Проводят конструирование элемента по одной из схем, приведенных на рис.1. Схему выбирают так, чтобы площадь принятых п о сортаменту арматурных стержней превышала найденную теоретически, минимально отличаясь от нее. Диаметры стержней и расстояния между ними выбираются с учетом конструктивных требований главы СНиП П-21-75. Если сжатая арматура по расчету не требуется или ее теоретическая площадь оказывается меньше I см^, при конструировании принимают F^=I см^.
4. Вычисляют величину h0 . Если она оказывается меньше ранее принятой, операции в соответствии с пп.2 и 3 проводят при новой величине h0 •
5. Подсчитывают стоимости бетона Cg, арматуры С&, а также суммарную стоимость у =Cg+Ca.
В прил.б приведены: значения внешних переменных параметров Ь , h , Rg; номер схемы в соответствии с рис.1, по которой проводили конструирование; значения Cg,Ca,у . При некоторых значениях внешних переменных параметров ни одна из схем не удовлетворяет всем требованиям главы СНиП П-21-75 (например, расстояния между стержнями оказываются меньше допустимых). Для этих случаев значение у не приведено - внутренняя задача оптимизации решения не имеет.
Данные прил.б позволяют без дополнительных вычислений поставить в соответствие любому набору значений внешних переменных параметров значение целевой функции у .
Из прил.б видно, что задача оказалась многоэкстремальной.
ТО
1
В дальнейшем в тексте настоящих Рекомендаций для краткости под термином "оптимизация железобетонных конструкции" принято понимать оптимальное проектирование железобетонных конструкций
3