Руководство по составлению региональных таблиц нормативных и расчетных показателей свойств грунтов
Купить бумажный документ с голограммой и синими печатями. подробнее
Цена на этот документ пока неизвестна. Нажмите кнопку "Купить" и сделайте заказ, и мы пришлем вам цену.
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Документ предназначен для составления таблиц, прогнозирующих нормативные и расчетные значения показателей механических свойств грунтов различных геолого-генетических комплексов в районах их распространения. Содержит общие теоретико-методические положения, касающиеся выбора объекта исследования (региона, типа грунтов и пр.) и методов обработки экспериментального материала, а также описания основных этапов процедуры составления таблиц, включая математические формулы для ручного и машинного счета. Приведены примеры составления региональных таблиц по конкретным регионам, даны описание и текст программ для ЭВМ "Наири-2". Для инженеров-геологов, занимающихся проблемой многократного использования материалов инженерно-геологических изысканий.
Оглавление
Предисловие
1. Общие положения
2. Предварительная геолого-статистическая обработка экспериментальных данных
3. Предварительное исследование информативности косвенных признаков (показателей физических свойств пород)
4. Выбор и построение прогнозирующих уравнений
5. Построение толерантного предела для прогноза расчетных характеристик грунтов
6. Исследование устойчивости найденных зависимостей и определение области их применимости
7. Построение таблиц
8. Рекомендации по оформлению результатов исследований и использованию алгоритмов и программ
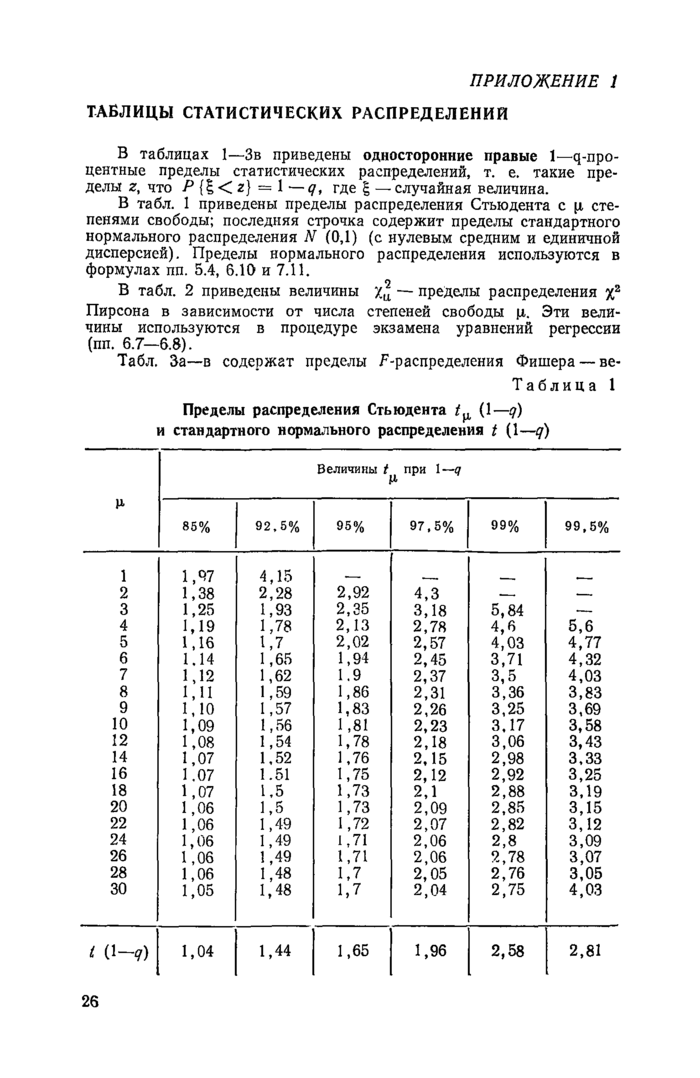
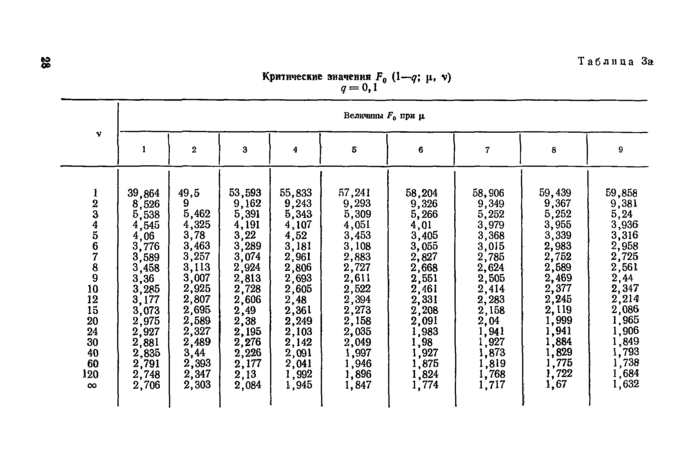
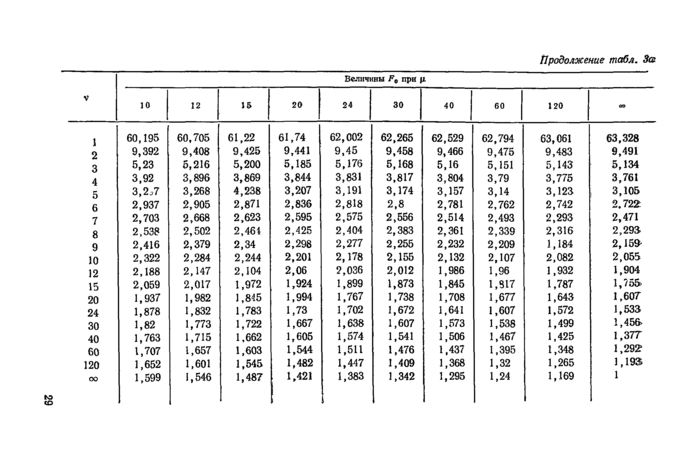
Приложение 1. Таблицы статистических распределений
Приложение 2. Рекомендуемая методика расчленения неоднородных выработок
Приложение 3. Пример составления региональной таблицы
Приложение 4. Программы построения уравнений между обобщенными значениями показателей для ЭВМ "Наири-2"
Рекомендуемая литература
| Дата введения | 01.01.2021 |
|---|---|
| Добавлен в базу | 01.10.2014 |
| Актуализация | 01.01.2021 |
Этот документ находится в:
- Раздел Строительство
Организации:
| Разработан | ПНИИИС Госстроя России | ||
| Издан | Стройиздат | 1981 г. | |
| Утвержден | ПНИИИС Госстроя СССР |
ГОСТ 19912-81Грунты. Метод полевого испытания динамическим зондированием. Заменен на ГОСТ 19912-2001.ГОСТ 20069-81Грунты. Метод полевого испытания статическим зондированием. Заменен на ГОСТ 19912-2001.ГОСТ 20522-75Грунты. Метод статистической обработки результатов определения характеристик. Заменен на ГОСТ 20522-96.- СНиП II-15-74 Основания зданий и сооружений
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26
стр. 27

стр. 28
стр. 29
стр. 30
ПНИИИС Госстроя СССР
Руководство
по составлению
региональных
таблиц
нормативных
и расчетных
показателей
свойств грунтов
Москва 1981
ПРОИЗВОДСТВЕННЫЙ И НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ПО ИНЖЕНЕРНЫМ ИЗЫСКАНИЯМ В СТРОИТЕЛЬСТВЕ (ПНИИИС) ГОССТРОЯ СССР
РУКОВОДСТВО ПО СОСТАВЛЕНИЮ РЕГИОНАЛЬНЫХ ТАБЛИЦ НОРМАТИВНЫХ И РАСЧЕТНЫХ ПОКАЗАТЕЛЕЙ СВОЙСТВ ГРУНТОВ
МОСКВА СТРОЙИЗДАТ 1981
i m
«-~2
*U (I
1-n).
(5)
7= 1
Аналогично вычисляются и коэффициенты корреляции г(х<, у).
3.11. Парные коэффициенты корреляции между обобщенными характеристиками инженерно-геологических элементов вычисляются по формуле
т
г* (Х/, X,)
У т1 (— ) (xiih-xi)
7=1_
(6)
т
*/ С*»-*)* 2 т> (*//—**)■
/=i
(/, 1=1, 2..... п\ аналогичная формула справедлива и^для r*(xt, у).
В формуле (6) средние поэлементные значения хц и у/ вычисляются по всем индивидуальным значениям показателей х к у, входящим в /-й элемент [формулы (2), (3)]; общие средние значения вычисляются по формуле
т т
_J_
т
2т/
/=i
/в=1
т1Ур xt =
2т/ '=1
7-1
Во всех случаях веса в формулах (6) и (7) равны числу определений механического свойства у в пределах /-го элемента.
3.12. Важными характеристиками связи являются частные коэффициенты корреляции, характеризующие для любых двух показателей степень их зависимости, очищенной от влияния остальных показателей.
Для их вычисления рассматривается симметричная матрица парных коэффициентов корреляции:
(Г(х 1, Xi)r(Xi, х,)...г(х1( хп)г(х1,у)
г (х2> *л) Т (х2, х2) ... г (х2, Хп) Т (х2, у)
.....................
Г (Х„, Хл) Г (хп, хг) ...г (х„, х„) г (х„, у)
Г (у, Хл) г (у, х2) ... г (.у, х„) г (у, у)
в случае обобщенных показателей элементами матрицы R являются величины г* (6). Тогда частные коэффициенты корреляции р(Х|, у) фактора Xi с функцией у вычисляются по формуле
_11 У1' Я+1> ||_
V II R1' 0 II • || fl(n+l. я-И) ||
(9)
где !#«. Я||—минор матрицы R, получаемый после вычеркивания i-й строки и /-го столбца.
3.13. Выбор оптимального набора факторов-аргументов, как правило, осуществляется с применением ЭВМ в ходе построения прогнозирующего уравнения. Наиболее употребительные методы выбора описаны далее.
Ю
Если в используемой программе отсутствует формализованная процедура отбора информативных показателей, они могут быть выбраны на основе изучения и сопоставления величин парных и частных коэффициентов корреляции, рассчитанных автоматически или вручную.
3.14. Независимо о г того, использовалась ли автоматизированная система отбора информативных показателей или они были выбраны на основе анализа парных и частных коэффициентов корреляции, полученный набор аргументов может быть откорректирован на основе содержательных соображений.
Например, если парные и частные коэффициенты корреляции нескольких факторов-аргументов с фактором-функцией в пределах одной группы (см. п. 3.2) имеют близкие выборочные значения, то допустимо выбрать в качестве аргумента уравнение регрессии любой из этих факторов, руководствуясь соображениями о точности их определения, увеличении объема массива исходных данных, стандартизации входа в таблицы и т. п.
Следует помнить, что окончательный выбор прогнозирующего уравнения может быть сделан только после процедуры «экзамена» (см. разд. 6). До этого момента рекомендуется рассматривать несколько различных уравнений, если они дают примерно одинаковую точность прогноза механической характеристики.
3.15. Наряду с показателями самих физических свойств аргументами прогнозирующего уравнения в принципе могут быть и их простейшие преобразования’(логарифмы,-степени, смешанные произведения и пр.), поэтому набор аргументов Хи Х2, ...» Хр (см. разд. 4) может не совпадать с исходным набором показателей физических СВОЙСТВ Хи *2, ...» хп (см. п. 2.6).
4. ВЫБОР И ПОСТРОЕНИЕ ПРОГНОЗИРУЮЩИХ УРАВНЕНИЙ
4.1. Построение прогнозирующего уравнения для того или иного механического показателя, как правило, сводится к оценке параметров линейных зависимостей
У =3°о + + + ••• + ДрХр, (10)
где У, Хи ...» ХР—либо исходные показатели механического и нескольких физических свойств (у, Хи Хп), либо простейшие преобразования этих показателей (например, логарифмы).
4.2. Выбор конкретного вида зависимости типа (10) осуществляется на основе предварительного анализа точечных корреляционных графиков либо путем пробной аппроксимации имеющихся данных кривыми разного вида с последующим сравнением качества прогноза. Как показывает опыт, непосредственная оценка параметров криволинейных зависимостей (в частности, полиномиальных) не вполне корректна, так как природная криволинейность зависимости тех или иных показателей, как правило, сопровождается изменчивостью остаточного разброса. Поэтому в таких случаях рекомендуется путем преобразования исходных факторов подбирать для аппроксимации возможно лучшие линейные зависимости типа (10).
4.3. Практика показывает, что применять преобразования исходных факторов чаще всего приходится при прогнозе модуля деформа- 1
ции (Я) и удельного сцепления (с). В частности, удовлетворительное качество прогноза обычно дают уравнения вида:
lg Я — а0 -|- агХх +••• -Ь а,пХп\ (11)
lg с = а0 "Ь aix\ + • • • + апхп> (12)
где Хи хп — исходные показатели физических свойств.
4.4. Для оценки параметров ао, вь •••» аР зависимости (10) применяется в той или иной модификации метод наименьших квадратен (МНК). Ниже в пп. 4.5—4.7 приводятся основные расчетные методы для построения зависимостей между индивидуальными значениями показателей с помощью традиционного МНК, в пп. 4.8— 4.10 — методы построения зависимостей между обобщенными значениями показателей, для которых рекомендуется использовать взвешенный МНК. Все формулы приводятся в обычном и матричном виде. Использование матричной записи значительно упрощает алгоритм вычислений, однако для некоторых типов ЭВМ такие возможности ограничены размерами оперативной памяти и недостатками математического обеспечения.
4.5. При исследовании зависимостей между индивидуальными значениями показателей исходят из модели
У] = о0 + fl^i/ + a2X2j + ... + dpXpi 4- е/, (13)
где /=1, 2, ...» т — индекс индивидуальных значений (т — общее число параллельных определений показателей), sj — случайные ошибки, подчиняющиеся нормальному распределению, не зависящие от факторов-аргументов и друг от друга, Mej = 0, Dej=a2 (a2 — так называемая условная дисперсия показателя У).
Для матричной записи этой модели удобно ввести матрицу независимых переменных X:
|
1 X,, х,л...хп\ 1 Х12 Х22 ... хр2 1 |
(14.) |
|
1 • -Крт / |
а также вектор-столбец Y механического показателя с коордипа-
тами Уj (/=1, 2, .... т), вектор параметров а с координатами а<
(1=0, 1, .... р) и вектор ошибок е. Тогда уравнение (13) запишется так:
Y = x"Ve. (15)
4.6. Основное требование обычного МНК заключается в минимизации суммы квадратов расстояний от эмпирических точек {Yj, -Xij. Xpj} до прогнозирующей плоскости (10):
т
2 1 Yl -ао- «Л/- • • • - Яр*р/1а => min. (16)
/=1
Оценки <Xi, ...» ap параметров alt ..., av, доставляющие минимум функционалу (16), являются корнями так называемой системы нормальных уравнений:
|^11а1 + k 12a2 + • • • + kif/Zp = kx\
(17)
^2lal 4" ^22®2 “f* • • • + k^pCCp = k2\
kpi*l 4" kp2C^2 + . . . + kppCLp = kp,
коэффициентами которой служат элементы симметричной матрицы К выборочных ковариаций
1 т
*!/ = — 2 W/-X|)(X|/-X|) (I. / = 1-р), (18)
m /=i
а также элементы столбца свободных членов
Поэтому величины at
(<=1. 2..... р)
II К(0 II
ОС/ =-
1 1X1
вычисляются по формуле (20)
(19)
где ||КII—определитель матрицы К (18), а IIWMl — определитель матрицы, которая получается из К после замены i’-го столбца
столбцом свободных членов к (19).
После этого оценка а о свободного члена зависимости (10) определяется по формуле
«,-У-аД-...^ аРХр. (21)
(22)
В матричной форме систему (17) можно записать в виде
ХЧСа = Хт Y,
где Хт —• матрица, транспонированная к X, a — вектор-столбец оценок a* (i=0, 1, р). Тогда МНК — оценка вектора а дается
выражением
~a = (Хт Х)—1ХТ Y-. (23)
4.7. Оценкой условной дисперсии о2 является так называемая остаточная дисперсия
s’ =-1—~ 2 [Уj—aa~a1Xii— ... - apXpjP. (24)
m-Р— 1 ~
которая служит мерой качества аппроксимации исходных данных.
4.8. При построении уравнения связи между обобщенными характеристиками грунтов принимается следующая модель для обобщенных значений:
Yf = во 4“*h.Xif + ••• + apXpf 4-6/ (/ ==* 1 т), (25)
где У*, Xij, ..., Xpj — средние значения какого-либо из показателей механических свойств у и показателей физических свойств х\ (или их преобразований), полученные по всем индивидуальным зна-
13
чениям в пределах /-го инженерно-геологического элемента; 6j подчиняются нормальному распределению, не зависят от факторов-аргу-
сг2
ментов и друг от друга Мб/ = 0, D6/ = “^—, где rrij — число
определений показателя у в пределах /-го элемента.
Введя матрицу обобщенных показателей физических свойств X,
■—V
вектор-столбец обобщенных механических показателей Y длины т, —► —►
(26)
а также векторЗ а и б аналогично п. 4.5, модель (25) можно записать так:
Y = X<z-f 6.
4.9. Основное требование взвешенного МНК состоит в минимизации функционала
т
-2т/ [Yi — ao — ai*il — ••• — аДр/]2=>min. (27)
/=1
Оценки cto, Oi, .... аР параметров a0, fli, ..., «pt доставляющие минимум функционалу (27), определяются по формулам (20) —(21), с той разницей, что элементы ковариационной матрицы К и столбца
k даются формулами:
т
ktl = —- V т, (Хц - X,) (Х„ ~ Xt) (г. / = 1 - п), (28)
2*/ #
/=1
т
*< = ~-Vm^X,,-*,) (У/-У) (i=lr«), (29)
/=1
а общие средние Р, .Yi ..., Хр — формулой (7).
(30)
В матричной форме система нормальных уравнений имеет вид
|
( mx |
0 | |
|
wJ |
т2 | |
|
\ |
\ 0 |
mm |
XTWX а = X*WY, где W — диагональная матрица:
(31)
Оценка вектора а дается выражением
(32)
~а = (ХЛУХГ'ХЛУУ.
4.10. Мерой качества аппроксимации является величина оста^ точной дисперсии
m
*1 = ~m-p-i V] ПО -°o- «Л/ - ... - «Л/]8 • (33)
/Я
4.11. Важным пунктом, во многом определяющим окончательный вид прогнозирующего уравнения, является использование критериев проверки статистической значимости зависимости в целом (общий г-критерий, п. 4.12) и каждого из аргументов в отдельности (частный ^-критерий, п. 4.13). При построении таблиц нормативных характеристик проверка значимости результатов но этим критериям является необходимым условием использования построенных уравнений.
4.12. Для построения общего F-критерия необходимо вычислить величину
т
ф2 = 2 (*7-?Л (34)
/=1
где Yj = а0 + + • • • + af>Xpj (/ — 1 + т) (35)
суть прогнозные значения, получаемые по проверяемому уравнению для экспериментальных индивидуальных или обобщенных значений
т 1
/=1
определений
аргументов Хг/, .... Хр/\
т
показателей или У =*
при обработке инди-
видуальных параллельных т
= — при обработке обобщенных параллельных
1 Hi
определений показателей [см. обозначения по формулам (1)—(3)].
Для применения общего ^-критерия необходимо, задавшись надежностью (1—а)%, найти односторонний (1—а)-процентный предел /^-распределения с ц=р-И и v=m—p—1 степенями свободы (табл. 3, прил. 1 при q=а), т. е. число Fo(l—а; Ц, v). Тогда, если отношение
(36)
F «-SL s2 '
где ф2 вычисляется по формуле (34), a s2 — остаточная дисперсия [формула (24) для индивидуальных или формула (33) для обобщенных показателей], удовлетворяет условию
f >fo(1—<*; ц. v), (37)
то проверяемая зависимость статистически значима. В противном случае эта зависимость на выбранном уровне (1—а) % незначима. Как правило, рекомендуется использовать общий ^-критерий при 1—а=90 %.
4.13. Для построения частного F-критерия, проверяющего значимость каждого вводимого в зависимость (10) последнего аргумента ХР, необходимо наряду с величиной (34) иметь величину
15
Рекомендовано к изданию секцией методики, экономики и техники инженерных изысканий НТС ПНИИИС Госстроя СССР.
Руководство по составлению региональных таблиц нормативных и расчетных показателей свойств грунтов / ПНИИИС Госстроя СССР. — М.: Стройиздат, 198-1.— 55 с.
Предназначено для составления таблиц, прогнозирующих нормативные и расчетные значения показателей механических свойств грунтов различных геолого-генетических комплексов в районах их распространения. Содержит общие теоретико-методические положения, касающиеся выбора объекта исследования (региона, типа грунтов и пр.) и методов обработки экспериментального материала, а также описания основных этапов процедуры составления таблиц, включая математические формулы для ручного и машинного счета.
Приведены примеры составления региональных таблиц по конкретным регионам, даны описание и текст программ для ЭВМ «Наири-2».
Для инженеров-геологов, занимающихся проблемой многократного использования материалов инженерногеологических изысканий.
Табл. 9., ил. 4.
30213—479
Р -- Инструкт.-нормат., II вып. — 61—80. 3202000000
047(01)—81
© Стройиздат, 1981
ПРЕДИСЛОВИЕ
Действующая в настоящее время глава СНиП Н-16-74 допускает для предварительных расчетов оснований зданий и сооружений всех классов, а также для окончательных расчетов оснований зданий и сооружений II—IV класса и ряда других сооружений определение нормативных и расчетных значений прочностных и де-
{юрмационных характеристик по их физическим показателям табл. 1—3 прил. 2). Для отдельных районов указанная глава СНиП позволяет вместо таблиц прил. 2 использовать специально разработанные я согласованные с Госстроем СССР региональные таблицы характеристик грунтов, учитывающие инженерно-геологическую специфику этих районов.
В настоящем Руководстве изложена - методика статистического обобщения фондовых данных по физико-механическим свойствам рыхлых грунтов с целью составления региональных таблиц для прогноза прочностных и деформационных свойств грунтов по показателям их состояния, состава и строения (физическим свойствам). Методика позволяет построить оптимальные уравнения для косвенной оценки нормативных (средних) и расчетных (гарантированных с заданной надежностью) показателей механических свойств, характерных для грунтов определенных геолого-генетических комплексов в определенных районах их распространения, а также исследовать устойчивость и область применимости найденных зависимостей. В приложениях приведены необходимые статистические таблицы, рекомендуемая методика расчленения неоднородных выборок классификационных показателей свойств грунтов, а также описание программ для ЭВМ «Наири-2», реализующих основные моменты изложенной методики.
В Руководстве изложен разработанный в последние годы новый подход (исследование так называемых структурных зависимостей), направленный на изучение связей между показателями механических и физических свойств грунтов, обобщенными в пределах инженерно-геологических элементов — макроскопически однородных геологических тел, размеры которых (в плане) соизмеримы с размерами инженерных сооружений. Такая постановка задачи наилучшим образом соответствует поставленной цели — обеспечить косвенный прогноз нормативных и расчетных характеристик грунтов, применимых при расчетах взаимодействия инженерных сооружений и естественных основапий.
В Руководство включены методические положения, прошедшие к моменту выпуска достаточную практическую апробацию. Ряд методов, важных с точки зрения обобщения материалов изысканий прошлых лет, в настоящее время находится в стадии разработки. К ним относятся, в частности, методы прогноза прочностных характеристик грунтов на основе сопоставления величин сопротивления сдвигу т и параллельных определений физических свойств.
Объектами для проведения исследований, предусмотренных настоящим Руководством, являются грунты определенных геолого-генетических комплексов, имеющих достаточно широкое распространение. Разрабатывая региональные таблицы, следует рассматривать эти комплексы грунтов в пределах таксономических единиц инженерно-геологического районирования: регионов, областей, районов.
С учетом практических потребностей допустимо выделение регионов по условным признакам: территория города, области, район работ крупной территориальной изыскательской организации и т. п., но и в этом случае таблицы составляются для одного генетического типа грунтов.
Настоящее Руководство может использоваться двояко. Первый путь, вполне доступный геологу,— непосредственное использование программы для машины «Наири-2», приведенной в прил. 4, а также других программ, рекомендованных в тексте. Второй путь — использование разработанного алгоритма для составления программы для другого типа ЭВМ — осуществляется математиком.
Руководство составлено в Лаборатории математических методов ПНИИИС канд. геолого-минерал. наук Б. Г. Слепцовым при участии кандидатов техн. наук О. И. Игнатовой (НИИОСП), М. Т. Ойзер-мана и канд. геолого-минерал. наук Н. М. Хайме, под общим руководством д-ра геолого-минерал. наук М. В. Раца. В примерах прил. 3 использованы материалы изысканий института Эстпром-проект (гл. геолог А. Вило).
1* ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Таблицы для прогноза характеристик механических свойств по показателям состава, структуры и состояния грунтов следует разрабатывать для наиболее характерных для данного региона геолого-генетических комплексов пород, широко использующихся в качестве естественных оснований зданий и сооружений. Сбор фактического материала должен осуществляться таким образом, чтобы в статистическую совокупность, предназначенную для обработки, включались опытные данные, относящиеся, как правило, к грунтам одного и того же генезиса, полученные единым методом при стандартных условиях проведения эксперимента. Приборы и оборудование, используемые при испытаниях грунтов, должны удовлетворять требованиям получения равноценных результатов. Фактический материал должен представляться в форме специальных стандартных бланков или таблиц, удобных для перевода информации на носители ЭВМ (перфокарты, перфоленты и т. п.).
1.2. Для прогноза прочностных и деформационных свойств грунтов настоящим Руководством предусматривается использование экспериментальных определений модуля деформации Е или коэффициента сжимаемости а, а также величин угла внутреннего трения (р и удельного сцепления с, полученных при обработке результатов сдвиговых испытаний на отдельных монолитах. При этом таблицы составляются для тех показателей, которые фактически определяются при изысканиях и аргументированно используются при проектировании оснований на площадках данного региона. В тех случаях когда прогнозируемые показатели получены по несовершенной (с точки зрения проектирования) методике, прогнозные характеристики должны быть пересчитаны с помощью переходных коэффи-циентов, установленных специальным статистическим исследова-нием (например, коэффициенты перехода от компрессионного модуля деформации к штамповому).
5
1.3. Сфера практического применения табличных характеристик механических свойств грунтов определяется качеством и количеством фактического материала, используемого для построения таблиц, и характером статистической обработки этого материала. Для предварительных расчетов на стадии технико-экономического обоснования проекта можно ограничиться нормативными табличными характеристиками, дающими прогноз механических свойств грунтов в среднем (п. 1.4); таблицы нормативных характеристик могут быть получены достаточно стандартными и почти полностью автоматизированными методами обработки данных. Для окончательных расчетов оснований на стадиях технического проекта и рабочих чертежей (либо на стадии техно-рабочего проекта) следует пользоваться расчетными (гарантированными) характеристиками, величина которых учитывает точность косвенного прогноза обобщенных показателей механических свойств грунтов на отдельных площадках изысканий (п. 1.6). Для получения расчетных характеристик необходимы более детальный гсолого-статисгический анализ фактического материала (включая выделение инженерно-геологических элементов на представленных в нем объектах изысканий) и введение соответствующей структуры массива исходных данных.
2—136
1.4. Нормативным значением показателя некоторого механического свойства грунтов (фактора-функции) при фиксированных значениях показателей одного или нескольких физических свойств (факторов-аргументов) следует считать величину, которая дается уравнением регрессии данной функции по данным аргументам. Это уравнение строится методами корреляционно-регрессионного анализа на основе параллельных определений физических и механических Характеристик — обобщенных (пп. 4.8.—4.10) или индивидуальных (пп. 4.6—4.7). Составляя таблицы нормативных характеристик, можно сводить в одну таблицу результаты прогноза по нескольким уравнениям регрессии, охватывающим разные диапазоны изменения аргументов.
1.6. Необходимым условием применения таблицы нормативных характеристик является статистическая значимость зависимости, положенной в ее основу, и значимость каждого из факторов-аргументов (пп. 4.11—4.12). Количество параллельных индивидуальных наблюдений для построения уравнения регрессии должно быть порядка нескольких сотен (при условии представительности данных для всего изучаемого комплекса грунтов).
1.6. Точность косвенного прогноза обобщенных показателей механических свойств грунтов обусловлена в первую очередь природными особенностями корреляции между свойствами грунтов, специфичными для данного регионального гео л ого-генетического комплекса. Она связана с существованием некоторого остаточного разброса истинных обобщенных показателей механических свойств при одних и тех же показателях состава, состояния и строения грунтов для разных инженерно-геологических элементов в пределах всего изучаемого комплекса; характеристикой этого разброса является так называемая остаточная дисперсия нормативных характеристик (п. 5.2). Поэтому расчетным значением фактора-функции при фиксированных значениях факторов-аргументов следует считать величину, которая определяется как толерантный предел для наблюдений функций, имеющих вышеупомянутую остаточную дисперсию (п. 5.4).
1.7. Для вычисления расчетных значений фактора-функции дополнительным требованием к количеству и качеству фактического материала является достаточная представительность входящих в него данных по отдельным инженерно-геологическим элементам (минимум 5—10 определений фактора-функции в среднем на элемент).
1.8. Общая схема проведения гео л о го-статистического исследования с целью составления региональных таблиц включает в себя следующие элементы:
предварительный геологический анализ и статистическая обработка фактического материала;
исследование информативности косвенных признаков и выбор оптимального набора аргументов;
выбор вида прогнозирующего уравнения и его построение; оценка остаточного разброса прогнозируемого показателя, построение толерантных пределов для прогноза расчетных показателей;
исследование устойчивости и области применения найденных зависимостей путем проведения экзамена на независимом материале; построение таблиц на основе найденных зависимостей.
6
2. ПРЕДВАРИТЕЛЬНАЯ
геолого-статистическая обработка
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
2.1. В ходе предварительного геологического анализа эксперй* ментальных данных необходимо прежде всего отбраковать сомнительные индивидуальные значения всех показателей, вызванные повреждением монолитов при транспортировке и хранении, лабораторными ошибками или другими причинами.
2.2. Удобным способом предварительного анализа данных является изучение парных корреляционных точечных графиков показателей. В частности, на этих графиках бывают видны отдельные экспериментальные значения, резко выделяющиеся из общей тенденции зависимости. Наличие таких точек на нескольких графиках (т. е. по нескольким парам показателей) является достаточным основанием для того, чтобы информация, относящаяся к соответствующим образцам, была исключена из дальнейшего рассмотрения.
2.3. Необходимой составной частью предварительной обработки данных для оценки расчетных показателей свойств грунтов, помимо описанных выше процедур, является расчленение исходного массива информации на части, отвечающие опробованшо отдельных инженерно-геологических элементов, т. е. частей массивов горных пород с чисто случайной изменчивостью основных физико-механических показателей, сравнимых по площади с размерами проектируемых инженерных сооружений. Весь изучаемый комплекс должен рассматриваться как объединение инженерно-геологических элементов. Выделение инженерно-геологических элементов на каждой площадке изысканий, представленной в экспериментальном материале, производится в соответствии с установками нормативных документов (ГОСТ 20552-75).
2.4. Последовательной формальной методики расчленения неоднородных массивов горных пород в настоящее время еще нет. Для небольших площадок изысканий (площадью порядка 1 га) можно ограничиться исследованием генетической однородности толщи и анализом изменчивости свойств по глубине. На больших площадках необходимо подвергать выборки основных физических характеристик грунтов (число пластичности, коэффициент пористости, влажности и т. п.) анализу на статистическую однородность распределения. Рекомендуемая методика такого анализа изложена в прил. 2.
2.5. Вновь объединять выделенные на каждой площадке инженерно-геологические элементы, сходные по физико-механическим свойствам (например, используя известные критерии сравнения средних значений показателей), рекомендуется лишь для близко расположенных площадок (с расстоянием не более 1 км).
7
2.6. В результате предварительной отработки экспериментальных данных формируется массив для дальнейшей статистической обработки. Прогнозируя какой-либо конкретный показатель механического свойства грунтов, удобно представлять этот массив в виде матрицы:
2*
*11» *21» • *12» *22» •
*1/» *2J» *
xinu xtmt
*/1»
*/2»
» *Л1» У i » *Л2» У 2
xlb ••• i xnJ» У]
* xim» • * *» *л/я» Ут ‘
(1)
Здесь —результат определения t-го физического свойства на /-м образце; если проведено расчленение исходного массива информации (п. 2.3), то Xij есть среднее арифметическое значение показателей t-го свойства в пределах /-го инженерно-геологического элемента:
*// =
|
1 Щ] |
(2)
У) — соответствующие значения (индивидуальные или обобщенные) показателя механического свойства; п — число факторов-аргументов; т — число образцов (или число элементов); тц— число определений i-ro физического свойства в пределах /-го элемента.
2.7. В случае перехода к обобщенным характеристикам грунтов необходимо сохранить для дальнейших вычиелний (п. 5.2) величину так называемой внутриэлементной дисперсии фактора-функции:
(3)
2т/~“ т 1=1
/-1 /“1
где mj — число определений механического свойства, a yj и уц — соответственно среднее и частные значения показателя этого свойства в пределах /-го элемента.
3. ПРЕДВАРИТЕЛЬНОЕ ИССЛЕДОВАНИЕ ИНФОРМАТИВНОСТИ КОСВЕННЫХ ПРИЗНАКОВ (ПОКАЗАТЕЛЕЙ ФИЗИЧЕСКИХ СВОЙСТВ ПОРОД)
3.1. Отбор информативных показателей физических свойств грунтов должен осуществляться как на основе геологических соображений (пп. 3.2^—3.7), так и методами корреляционного анализа (пп. 3.9-—3.12). Рациональное сочетание формальных методов и геологического подхода при подборе информативного набора показателей позволяет сократить время машинного счета и приводит к более эффективному результату.
3.2. Имеющийся опыт показывает, что все показатели физических свойств грунтов могут быть условно разделены на три группы, внутри которых они тесно скоррелированы между собой.
К первой относятся показатели плотности, являющиеся в известной мерс характеристиками структуры породы: объемная масса у скелета грунта, объемная масса грунта уо при естественной влажности, пористость п или коэффициент пористости е. Если грунт
8
находится в водонасыщенном состоянии (степень влажности близка к единице), сюда же следует отнести естественную влажность W.
Ко второй группе относятся показатели состава, или «глинистости» грунта: пределы WPt WL и число пластичности 1Р, показатели грансостава, показатель консистенции /ь.
В тех случаях, когда грунт находится в состоянии неполного водонасыщения (G<0,8), можно выделить третью группу — показатели влажности, к которым относятся естественная влажность W и степень влажности G.
3.3. Показатели свойств грунтов внутри каждой группы (как непосредственно определяемые, так я рассчитываемые) в известной мере дублируют друг друга, поэтому в рациональный набор аргументов прогнозирующего уравнения, как правило, целесообразно включать нс более одного показателя из каждой группы. При прочих равных условиях предпочтение следует отдавать показателям, непосредственно определяемым в лаборатории.
3.4. Для глинистых водонасыщенных грунтов наиболее тесные связи прочностных показателей (по опыту исследований) наблюдаются с показателями второй группы (в частности, с содержанием глинистой фракции — например, для аллювия) и несколько менее тесные — с показателями первой группы.
3.5. Для глинистых неводонасыщенных грунтов или грунтов с переменной степенью влажности (например, лёссы) оптимальный набор показателей должен включать наряду с показателями первой и второй группы также степень влажности G или естественную влажность W.
3.6. Для песчаных грунтов прочностные и деформационные показатели наиболее тесно связаны с коэффициентом пористости при одновременном учете номенклатурного вида песка.
3.7. В необходимых случаях в качестве возможных аргументов прогнозирующих уравнений регрессии должны быть исследованы степень засоленности грунтов, содержание органического вещества и т. п.
3.8. Для предварительного визуального анализа степени и характера взаимосвязей между показателями целесообразно построение точечных графиков парных зависимсстсй прогнозируемого показателя от каждой из физических характеристик.
3.9. Формальное исследование информативности косвенных признаков основано на анализе парных и частных коэффициентов корреляции, характеризующих тесноту связи каждого из аргументов х\ с прогнозируемой характеристикой у.
m
2 (**/ */) /=1_
Г (*/, */) =
(U»l*n)e (4)
3.10. Парные коэффициенты корреляции между индивидуальными значениями показателей вычисляются по формуле
где тп — общее число параллельных определений показателей, а
9
1