Пособие по расчету крупнопанельных зданий. Выпуск 5. Расчет вертикальных упругих диафрагм на горизонтальные нагрузки (определение усилий и перемещений)
Купить бумажный документ с голограммой и синими печатями. подробнее
Цена на этот документ пока неизвестна. Нажмите кнопку "Купить" и сделайте заказ, и мы пришлем вам цену.
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Документ содержит методику и примеры статического расчета на горизонтальные нагрузки вертикальных диафрагм жесткости крупнопанельных зданий. Пятый выпуск пособия включает краткое описание алгоритмов расчета вертикальных крупнопанельных диафрагм жесткости, рассматриваемых как упругие системы на действие горизонтальных нагрузок по методам конечных элементов и рамной аналогии, основанных на дискретных расчетных моделях, с примерами расчета и программой для
для инженерно-технических работников проектных и строительных организаций.
Оглавление
Введение
1. Расчет упругих диафрагм методом конечных элементов
2. Расчет упругих диафрагм методом рамной аналогии
3. Примеры расчета вертикальных диафрагм методом рамной аналогии
4. Расчет вертикальных диафрагм методом конечных элементов в сравнение их с результатами расчета методом рамной аналогии
Приложение. Программа расчета вертикальных диафрагм на горизонтальные нагрузки
Список литературы
| Дата введения | 01.01.2021 |
|---|---|
| Добавлен в базу | 01.10.2014 |
| Актуализация | 01.01.2021 |
Этот документ находится в:
- Раздел Экология
- Раздел Строительство
Организации:
| Разработан | ЦНИИСК им. В.А. Кучеренко | ||
| Издан | Стройиздат | 1982 г. | |
| Утвержден | ЦНИИСК им. В.А. Кучеренко Госстроя СССР |
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26

стр. 27
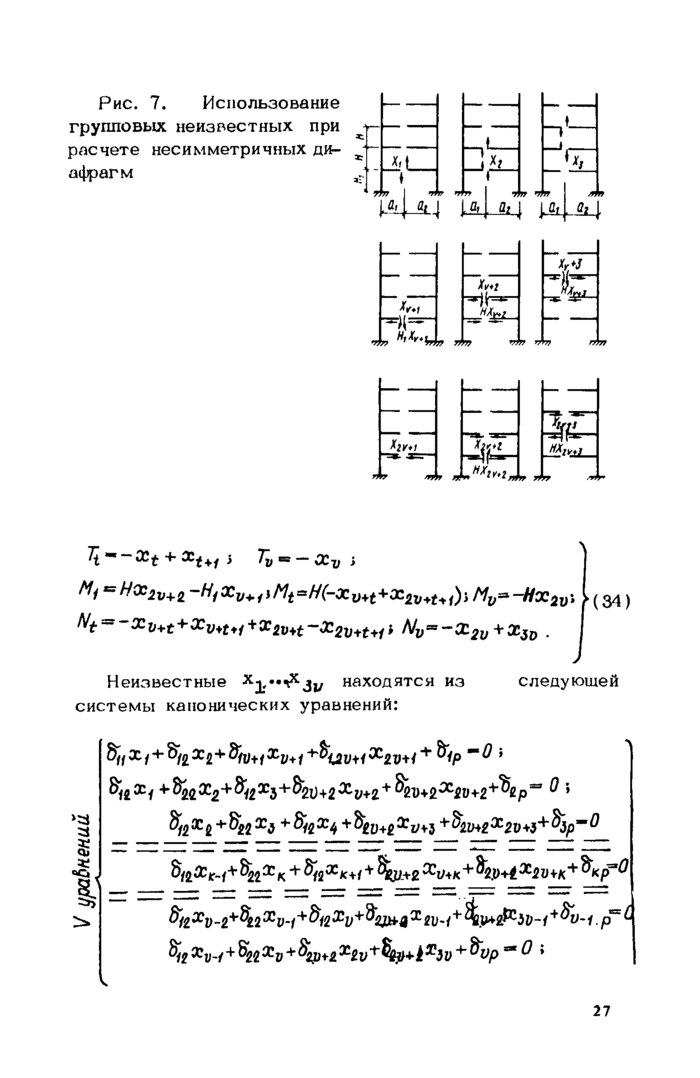
стр. 28

стр. 29

стр. 30
ЦНИИСК им. В. А. Кучеренко Госстроя СССР
Пособие
по расчету
крупнопанельных
зданий
Выпуск 5
Расчет
вертикальных упругих диафрагм на горизонтальные нагрузки
(определение усилий и перемещений)
Москва 1982
ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ институт СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ ИМ. В. А. КУЧЕРЕНКО (ЦНИИСК ИМ. В. А. КУЧЕРЕНКО)
ГОССТРОЯ СССР
ПОСОБИЕ ПО РАСЧЕТУ КРУПНОПАНЕЛЬНЫХ ЗДАНИЙ
Выпуск 5
Расчет
вертикальных упругих диафрагм на горизонтальные нагрузки
(определение усилий и перемещений)
Москва Сгройиздат 1982
|
да/ дх |
д/дх о | |||
|
Sy |
■ ~ |
ди/ду |
* |
О д/ду |
|
Пу |
ди/ду+ dvldx . 4 |
д/ду д/дх |
Ма три ua[£J] легко находится из соотношения (2) в том случае, если известны функции формы , Nj} Nk и/Ут.
В общем случае материал элемента может иметь начальные деформации f<S0) , обусловленные усадкой, температурными воздействиями и т. п. Кроме того, в толе элемента могут существовать и некоторые остаточные напряжения {£„] . Используя закон Гука, с учетом начальных деформаций и остаточных напряжений, записывается зависимость напряжений от деформаций: „ „ # . , . ,
{(Г} = [0] ({£}-{«.])+ {Го} , (5)
где [D\ — матрица упругости, коэффициенты которой зависят от характеристик материала КЭ. Компоненты напряжений в случае плоского напряженного состояния будут
|
1 - | |
|
J ~ |
(Ги . Т'ХУ . |
для
упругого, изотропного материала:
~ ~ У Оу ) I Е}
dy — (6у)0 (Gy~ V б~х) I Еу
+ IE*
Отсюда
■
|
У О / О О (/-У)/2 |
(о)
Столбец узловых сил, статически эквивалентный граничным напряжениям и действующим на элемент распределенным нагрузкам, запишется следующим об
разом:
ю
Распределенная нагрузка будет
Используя принцип возможных перемещений, можно установить связь (l), если рассматривать усилия/*}как внешние силы, которые вызывают внутри элемента напряженно-деформированное состояние, описываемое уравнениями (3) и (5). Согласно этому принципу, сумма работ всех внешних и внутренних сил на возможных перемещениях 6 £ ^ J равна нулю.
С помощью соотношений (2) и (3) запишем соответственно вариации перемещений и деформаций эле-мента: -[/К] 5({) i
»{*} .
Работа, совершаемая узловыми силами, равна сумме произведений сил на соответствующие им перемеше-
ния: c»U})T{*} .
Работа внутренних напряжений и распределенных массовых сил, отнесенная к единице объема, равна
&{«}т{<г}-& {?}{я} ,
НЛИ (*М)Т([в]Т{<ГН*П/“})-
Приравнивая [шботу внешних и внутренних сил и интегрируя по объему элемента, получим
(Ь{г)Ц>?}=(Ь{с1})т(/[в]г{б-}а\/~
(7)
У
11
Подставив (3) и (5) в (7), имеем
W-(/[«] TW[S] «у; {«} ум
У V
Сравнивая зависимости (1) и (8), получим
W~nB][D][B]dV-
V
Узловые силы от распределенной нагрузки будут
v
Узловые силы,обусловленные начальными деформациями,получаются в виде
{*<Л~/МИК*.}*!'
и узловые силы, вызванные начальными напряжениями, запишутся: ^ _ _/[fl]Tj <Г0] dV .
Матрица [£] является квадратной, ее порядок равен числу степеней свободы рассматриваемого КЭ. Значения коэффициентов этой матрицы зависят от геометрических и жесткостных характеристик КЭ и от принятого закона распределения компонетов перемещения или напряжения.
Выбор функций перемещений (напряжений) для КЭ является самым важным моментом в обшей процедуре МКЭ. Желательно, чтобы выбранные функции приводили к удовлетворению уравнений равновесия и совместности деформаций внутри конечного элемента, к отсутствию разрывов по перемещениям и напряжениям вдоль сторон смежных элементов В идеальном случае при бесконечном числе степеней свободы элемента можно получить точное решение,
12
1.3. Если цля расчета взят метоп перемещений, а следовательно, за основные неизвестные приняты узловые перемещения, то цля нахождения этих неизвестных необходимо составить соответствующее число уравнений равновесия узловых точек. Решением такой системы алгебраических уравнений определяются неизвестные узловые перемещения.
Составление ансамбля и дальнейшее решение полученной системы производится с помощью процедур, описанных выше.
В узлах могут быть приложены сосредоточенные внешние силы, тогда для сохранения равновесия в узлах дополнительно вводится матрица сил (грузовой
столбец):
Учет заданных перемещений также не составляет особых затруднений.
Решением общей системы линейных алгебраических уравнений получаем узловые перемещения. Из соотношений (3) и (5) могут быть найдены напряжения влю-любой точке элмента:
1.4. При решении задач методом конечных элементов формируется система линейных уравнений, на которую в зависимости от возможностей ЭВМ накладываются ограничения по количеству неизвестных и по ширине ленты. Для того чтобы увеличить возможности программ, основанных на МКЭ, приходится разделять конструкцию на подсистемы, т.е. применять так называемые суперэлементы, использование которых приводит к сокращению времени непрерывного счета, что очень важно при расчете обширных систем.
13
Суперэлемент можно рассматривать как обыкновенный КЭ, матрица жесткости и грузовой столбец узловых нагрузок для которого получается численным решением, а не по аналитическим формулам. Для каждого суперэлемента формируются канонические уравнения и грузовой столбец. Исключая при решении алгеораических уравнений перемещения внутренних узлов, получаем матрицу жесткости и грузовой столбец узловых нагрузок для внешних узлов суперэлемента, из которых формируется общая система канонических уравнений. Решая эту систему, получаем перемещения внешних узлов суперэлемента, по которым находятся перемещения внутренних узлов при обратном ходе. Далее по деформациям определяются напряжения в КЭ, из которых составлялся суперэлемент. Использование суперэлемента только одного уровня обычно бывает недостаточным, поэтому приходится прибегать к более высоким уровням; /1 -й уровень суперэлемента составляется в свою очередь из низших уровней.
1.5. Метод конечных элементов ввиду своей универсальности может быть использован практически при
решении всех инженерных задач. При решении задач МКЭ могут быть использованы не только элементы одного вида, по и элементы самых различных конфигураций, что позволяет использовать этот метод для решения комбинированных задач. В одних и тех же задачах могут быть использованы одновременно различные КЭ, что улучшает точность решения при том же числе неизвестных, например применение треугольных элементов наряду с четырехугольными для более точного описания граничной области.
1.6. Рассмотрим приложение МКЭ к расчету плоских диафрагм жесткости зданий. Диафрагмы обычно состоят из ортогональных систем стержней-колонн, ригелей и прямоугольных пластин (каркасно-панельные здания) или только из прямоугольных элементов (панельные здания). Такие конечные элементы соединяются между собой в узловых точках. При использовании МКЭ в форме метода перемещений на каждый узел плоской расчетной схемы накладываются три связи,
препятствующие повороту узла и его линейным смещениям по направлениям осей глобальной системы координат (комбинированные конструкции) и только две связи, препятствующие линейным смешениям (плоскостные конструкции без стержневых элементов).
Для построения канонической системы уравнений равновесия следует сначала получить матрицы жесткости для стержневого элемента и для прямоугольной пластины.
Получение матрицы жесткости для стержневого элемента не представляет трудности, поэтому перейдем к примеру получения матрицы жесткости для прямоугольного элемента в случае плоского напряженного состояния. Основные соотношения теории упругости записываются в виде зависимости Коши (4) и закона Гука:
«г - си сгх + с,г (Гу ; (9)<$„- С,е(Гх ■+• с,, (Гу >
Г*(/ " ,
или в матричном виде
{£} = [С] [ (Г)
|
> | ||||||||||||||
|
где
обратная связь G*
записывается в виде
И-&>]{«}.
Таким образом,
(10)
(11)
15
УДК 624.042 (1-198.6) +69.056.52
Рекомендовано к изданию Секцией прочности крупнопа-
нельных и каменных конструкций научно-технического совета Ц11ИИСК им. В.А. Кучеренко.
Пособие по расчету крупнопанельных зданий. Вып. 5. Расчет вертикальных упругих диафрагм на горизонтальные нагрузки (определение усилий и перемещений) /ЦНИИСК им. ВА. Кучеренко.-М.: Стройиздат, 1982. - 74 с.
Содержит методику и примеры статического расчета на горизонталь ные нагрузки вертикальных диафрагм жесткости крупнопанельных зданий.
Пятый выпуск пособия включает краткое описание алгоритмов расчета вертикальных крупно панельных диафрагм жесткости, рассматриваемых как упругие системы на действие горизонтальных нагрузок по методам конечных элементов и рамной аналогии, основанных на дис-
Жтных расчетных моделях, с примерами расчета и программой для
Ш.
Для инженерно-технических работников проектных и строительных организаций.
Табл. 12, ил. 25.
П Инструкт.-нормат., II вып. - 102-81
© Стройиэддт, 1982
ВВЕДЕНИЕ
В настоящее время разработано большое число различных методов расчета диафрагм на горизонтальные нагрузки. Некоторые из этих способов изложены в литературе, список которой приведен в настоящей брошюре. В проектной практике расчета диафрагм чаще всего используются методы:
основанные на применении метода конечных элементов и метода сеток;
основанные на применении теории составных стержней;
основанные на использовании строительной механики рамных стержневых систем.
Все эти методы только приближенно могут моделировать реальные системы и условия их нагружения, но, по-видимому, только первый, следуя принятой классификации, позволяет сблизить характеристики натуры и ее модели (однако в пределах возможностей ЭВМ). Второй и третий способы дают меньшие возможности, однако имеют перед первыми то преимущество, что не требуют обязательного применения мощных ЭЦВМ, а в случае наличия таковых позволяют существенно экономить дорогостоящее и дефицитное машинное время.
Метод конечных элементов (МКЭ) является наиболее универсальным машинным методом расчета конструкций, позволяющим в общем случае с помощью пластинчатых и объемных конечных элементов (КЭ) в совокупности со стержневыми элементами, связанными условиями совместности напряжений или деформаций, описать практически любую конструкцию. МКЭ особенно хорошо приспособлен к расчету зданий из сборных элементов и композитных конструкций.
За последние годы опубликовано много работ, в которых подробно описывается идея метода конечных элементов (например, в работах [5, 17, 23])# Применительно к расчету рассматриваемых в данной брошюре сборных диафрагм специфика решения задачи в упругой постановке сводится к учету податливости стыковых соединений, характеристики которых даны в выпуске 1 этой серии fl5j.
Насчет диафрагмы по МКЭ начинается с предварительного расчленения ее фиктивными разрезами на конечные элементы, обычно прямоугольные или треугольные, после чего определяются матрицы жесткости или податливости-для каждого КЗ в зависимости от того, в какой форме используется МКЭ - в форме метода перемещений или в форме метода сил. Затем описываются условия совместности работы элементов -осуществляется объединение их в единую систему, моделирующую реальную диафрагму. В местах концентрации напряжений или на участках, где требуется более точный учет деформаций или напряжений, полезна дополнительная разбивка на КЗ. К таким участкам в сборных диафрагмах относятся опорные зоны перемычек между панелями.
При расчете конструкций МКЗ формируется система линейных уравнений, число которых быстро возрастает по мере роста числа КЗ, на которые разбивается система, поэтому применение этого метода невозможно при наличии маломощных машин.
Способы расчета диафрагм, основанные ца применении теории составных сержней, вошли в практику несколько раньше, чем основанные на использовании МКЗ. Впервые теория составных стержней в ее современной постановке была разработана А. Р. Ржанииыным [18] еще в 1948 г. , однако для диафрагм зданий она получила применение значительно позже благодаря работам П. Ф. Дроздова (З, 4 Э.Е. Сигалова, В.И. ЛишакаМ и других авторов. Распространение способов расчета составных стержней, связи сдвига которых равномерно распределены вдоль длины стержня, на расчет диафрагм заключается в замене сосредоточенных связей-4
перемычек эквивалентными им по жесткости связями, равномерно распре целенными по всей высоте этажа. Этот метоц эффективен в вычислительном отношении цля высоких зцаний, а их точность в этом случае соответствует метоау рамной аналогии при монотонно изменяющихся по высоте нагрузках и постоянной жесткости элементов.
Метоц рамной аналогии при расчете циафрагм с проемами прецполагает моделирование пилонов диафрагм стойками рамы, а перемычек циафрагм - ригелями рамы. Так же как и в методах, основанных на теории составных стержней, при расчетах с использованием рамной аналогии, считается справедливой гипотеза плоских сечений как цля пилонов, так и цля перемычек. Эго влечет за собой принципиальное ограничение возможностей моделирования действительных эпюр напряжений и деформирования сечений, отсутствующее в методах расчетов с использованием МКЭ, метода сеток или других методов теории упругости. Существенным недостатком второго и третьего методов расчета диафрагм является отсутствие возможности при их использовании оценить концентрацию напряжений, особенно в угловых участках проемов. Оба эти метода имеют преимущества перед равным в сравнительной простоте вычислений. Эго преимущество может быть использоа вано только в том случае, когда свойственные этим методам погрешности не будут недопустимо велики.
Возникает вопрос о степени точности результатов, получаемых при использовании второго и третьего методов расчета. В настоящем выпуске приводятся расчет вертикальных циафрагм методом рамной аналогии.
В качестве эталонных приняты результаты, полученные при расчете тех же циафрагм по МКЭ. В рассматриваемых далее примерах расчета сделана оценка влияния лоаэтливости горизонтальных швов сборных циафрагм на величины усилий и перемещений, возникающих в конструкции под действием горизонтальных сил.
Рассмотрение плоских циафрагм в настоящем выпуске связано как с использованием их ь качестве зле-
5
мента жесткости каркасно-панельных конструкций, так и в качестве составной части пространственной системы взаимно пересекаюшихся стен сборных крупнопанельных зааний.
При разработке данного выпуска пособия использованы результаты теоретических исследований крупнопанельных стен (диафрагм) при действии горизонтальных нагрузок, проведенных отделением сейсмостойкости сооружений, отделением крупнопанельных и каменных зданий и отделением вычислительной техники ЦНИИСК им. Кучеренко.
Программа для ЭВМ по методу рамной аналогии разработана канд. техн. наук Л.Л. Сабсовичем, инж. Д.А. Ржаницыным при участии кандидатов техн. наук Б.Е. Денисова и В.М. Дорофеева; программа по методу конечного элемента разработана канд. техн. наук ГМ Чентемировым.
В данном выпуске рассмотрены крупнопанельные диафрагмы в упругой стадии их работы с одним радом проемов.
Настоящий выпуск пособия разработан д-ром техн. наук С.В. Поляковым, кандидатами техн. наук В.Л. Мусиенко, Б.Е. Денисовым и Г.М. Чентемировым под общей редакцией д-ра техн. наук, проф. С.В. Полякова, д-ра техн. наук А Р. Ржаницына, д-ра техн. наук Н.В. Морозова.
1. РАСЧЕТ УПРУГИХ ДИАФРАГМ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ
1.1. При расчете методом конечных элементов (МКЭ) конструкций здания последние заменяются совокупностью плоских и пространственных сплошных элементов и стержней, связанных между собой в отдельных точках (узлах) и отвечающих условиям равновесия и совместности. МКЭ особенно хорошо приспособлен к расчету зданий из сборных элементов, поскольку позволяет учесть упругую податливость продольных и поперечных швов. Применительно к расчету несущих конструкций зданий процедура МКЭ состоит в следующем:
сплошная конструкция разделяется воображаемыми линиями на конечные элементы;
предполагается, что элементы связаны между собой в узловых точках, расположенных на их границах. В наиболее распространенном варианте МКЭ перемещения этих точек принимаются за не честные (МКЭ в форме метода перемещений);
выбирается система функций, однозначно определяющая перемещения внутри каждого конечного элемента через перемещения узловых точек
составляются уравнения равновесия внешних и
внутренних сил в узловых точках. Решением полученной системы алгебраических уравнений определяются неизвестные перемещения узлов;
по полученным перемешениям^можно определить напряжения в любой точке i -го КЭ.
По существу, этот метод эквивалентен минимизации полной потенциальной энергии системы. МКЭ в форме метода перемещений представляет модификацию метода
1
Рис. 1. Прямоугольный плоский конечный элемент
г
Ритца, основанного на задании поля перемещений системы в виде набора частных полей в конечных элементах.
Рассмотрим теперь вкратце формирование разрешающих уравнений МКЭ в форме метода перемещений.
Представление действительной конструкции совокупностью КЭ, связанных между собой лишь в узловых точках, требует, чтобы напряженное и деформированное состояние в каждом элементе однозначно определялось через узловые перемещения,
1.2. Матрица жесткости для КЭ определяет связь между узловыми перемещениями и узловыми усилиями в нем.
В качестве примера покажем получение матрицы жесткости для прямоугольного КЭ в случае плоского напряженного состояния, которое будет определяться восемью узловыми линейными перемещениями (рис. 1).
Влияние смежных элементов расчетной схемы заменим совокупностью усилий Я для каждого узлового перемещения q . Тогда связь между узловыми усилиями и узловыми перемещениями можно записать в виде
tpM*][?M*vM*J. и)
где
где
, Qg] -матрица-столбец узло-вых усилий;
[q]T = [qiy(l2^.-, £*] ~ матрица-столбец узло-
М -
ш-
' вых перемещений!
искомая матрица жесткости, которая определяет упругие свойства вассматоиваемого КЭ* силы, уравновешивающие действующие на элемент распределенные нагрузки;
8
[#£o] - узловые силы, возникающие в результате начальных деформаций.
Для нахождения матрицы жесткости [Л] необходимо задаться законом распределения компонентов перемещений или напряжений в конечном элементе. От того, насколько удачно выбраны функции для этих компонентов, зависит и точность решения.
Яс
Я}
Ь
Яш
{(/} NjiNk ',Nm]
(2)
Запишем выражение для компонентов перемещения конечного элемента|(/|=|«(р| через вектор узловых перемещений г«] •
где [N]\- прямоугольная матрица размером 2x8, элементы которой зависят от координат рассматриваемой точки:
Я1
Функции формы /Yj, Nj, А^. должны быть выбраны
таким образом, чтобы при подстановке в формулу (2) координат узлов получались соответствующие узловые перемещения, т. е. :
NiiXiiyi)
Nl (зс/ (хк i У к) * > Угп ) »
где Е - единичная матрица.
Если известны перемещения во всех точках элемента, то используя зависимости Коши, можно получить выражение для деформаций в этих же точках:*
13)
W-MU1,
где[в]~ прямоугольная функциональная матрица представляющая результат действия оператора зависимостей Коши на функции формы элемента.
В случае плоского напряженного состояния деформации определяются с помошью известных соотношений через смещения
9