Методические указания по определению гидрогеологических параметров при разведке и освоении угольных месторождений
Купить бумажный документ с голограммой и синими печатями. подробнее
Цена на этот документ пока неизвестна. Нажмите кнопку "Купить" и сделайте заказ, и мы пришлем вам цену.
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
В документе изложена методика определения основных фильтрационных параметров водоносных горизонтов по результатам опытных откачек и гидрогеологических наблюдений за режимом подземных вод
Оглавление
Введение
1. Краткая характеристика основных фильтрационных параметров
1.1. Коэффициент фильтрации и проводимость
1.2. Водоотдача и упругая водоотдача
1.3. Коэффициенты уровнепроводности и пьезопроводности
1.4. Некоторые дополнительные фильтрационные параметры
2. Основные дифференциальные уравнения фильтрации и их решения в связи с определением фильтрационных параметров
2.1. Исходные дифференциальные уравнения фильтрации
2.2. Гидродинамическая типизация пластов, граничные и начальные условия фильтрации
2.3. Простейшие аналитические решения установившейся фильтрации, используемые для определения фильтрационных параметров
2.4. Основные решения неустановившейся фильтрации, используемые для определения фильтрационных параметров
2.5. Основные сведения о методах определения фильтрационных параметров по результатам откачек
3. Методика интерпретации результатов опытных откачек
3.1. Качественная интерпретация результатов и предварительная опенка общих закономерностей фильтрации при кустовых откачках
3.2. Основные способы определения фильтрационных параметров в неограниченном изолированном однородном горизонте
3.3. Определение параметров изолированных водоносных горизонтов при типовых граничных условиях
3.4. Определение параметров слоистых водоносных толщ при установившемся режиме фильтрации с учетом перетекания
3.5. Методы определения параметров слоистых толщ по результатам опытных откачек при неустановившемся режиме с учетом перетекания
3.6. Определение параметров слоистых водоносных толщ с помощью приближенных решений, полученных методом интегральных соотношений
3.7. Некоторые замечания о методах интерпретации одиночных опытных откачек
4. Методика интерпретации результатов гидрогеологических наблюдений, проводимых в период эксплуатации месторождений
4.1. Качественная интерпретация результатов гидрогеологических наблюдений
4.2. Определение основных фильтрационных параметров по результатам гидрогеологических наблюдений
4.3. Интерпретация результатов опытно-эксплуатационного водопонижения
5. Специальные методы определения фильтрационных параметров
5.1. Операционный метод
5.2. Метод В.Б. Георгиевского
5.3. Определение гидрогеологических параметров на электрических моделях
Приложение 1. Специальные математические функции, используемые при гидрогеологических расчетах
Приложение 2. Таблица значения функции -Ei
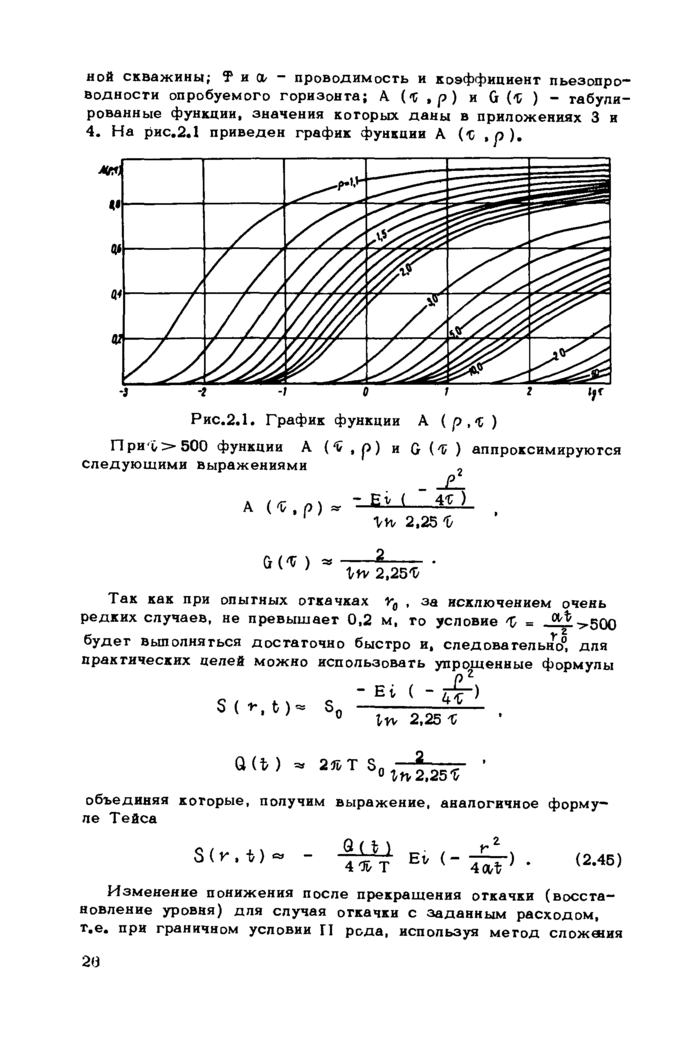
Приложение 3. Таблица значения функции A
Приложение 4. Таблица значения функции G
Приложение 5. Интеграл вероятности Ф
Приложение 6. Таблица значения функции S
Приложение 7. Таблица значения функции T
Приложение 8. Таблица значения функции W
Приложение 9. Таблица значения функции H
Приложение 10. Значения функции e в степени x
Приложение 11. Таблица значения функции Ei
Литература
| Дата введения | 01.01.2021 |
|---|---|
| Добавлен в базу | 01.01.2019 |
| Актуализация | 01.01.2021 |
Этот документ находится в:
- Раздел Экология
- Раздел Строительство
Организации:
| Разработан | ВНИМИ | ||
| Издан | ВНИМИ | 1974 г. | |
| Утвержден | Министерство угольной промышленности СССР |
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16
стр. 17
стр. 18

стр. 19

стр. 20

стр. 21

стр. 22

стр. 23
стр. 24
стр. 25
стр. 26
стр. 27

стр. 28

стр. 29
стр. 30
МИНИСТЕРСТВО УГОЛЬНОЙ ПРОМЫШЛЕННОСТИ СССР ВСЕСОЮЗНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ГОРНОЙ ГЕОМЕХАНИКИ И МАРКШЕЙДЕРСКОГО ДЕЛА ВНИМИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ОПРЕДЕЛЕНИЮ ГИДРОГЕОЛОГИЧЕСКИХ ПАРАМЕТРОВ ПРИ РАЗВЕДКЕ И ОСВОЕНИИ УГОЛЬНЫХ МЕСТОРОЖДЕНИЙ
(Одобрено и рекомендовано к применению Геологическим Управлением Минуглепрома СССР)
Ленинград
1974
МИНИСТЕРСТВО УГОЛЬНОЙ ПРОМЫШЛЕННОСТИ СССР ВСЕСОЮЗНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ГОРНОЙ ГЕОМЕХАНИКИ И МАРКШЕЙДЕРСКОГО ДЕЛА ВНИМИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ОПРЕДЕЛЕНИЮ ГИДРОГЕОЛОГИЧЕСКИХ ПАРАМЕТРОВ ПРИ РАЗВЕДКЕ И ОСВОЕНИИ УГОЛЬНЫХ МЕСТОРОЖДЕНИЙ
(Одобрено и рекомендовано к применению Геологическим Управлением Мкиугпепрома СССР)
Ленинград
1974
1.3* К оэффициенты уровнепроводности и пьеэопроводносги
|
% |
(1.4)
(X/
1.3.1. Коэффициент уровнепроводности ( а ) является расчетным параметром неустановившейся безнапорной фильтрации, характеризующим скорость сработки статических запасов. Он определяется соотношением
где Иср - средняя мощность безнапорного горизонта; эта величина не является постоянной, а меняется в зависимости от понижения уровня на границе и от времени. Поэтому величина коэффициента уровнепровоДности зависит от условий проведения эксперимента, по результатам которого она была определена.
1.3.2. Коэффициент пьезопроводности ( ffc* ) характеризует упругий режим фильтрации и является аналогом коэффициента уровнепроводности для условий неустановившейся фильтрации в напорных водоносных пластах. Коэффициент пьезопроводности связан со сжимаемостью водоносных пород зависим остью
Как и коэффициент уровнепроводности, коэффициент пье-зопроводности зависит от понижения уровня и от времени дренирования, гак как коэффициент сжимаемости зависит не только от приращения нагрузки, но и от ее абсолютной величины. Но, как правило, этим обстоятельством можно пренебречь. Более существенным является тог факт, что при откачках в напорных водоносных слоях обычно получают не коэффициент пьеэопроводносги в 'чистом' его виде, а некоторую обобщенную величину, учитывающую поступление воды через глинистые слои, контактирующие с опробуемым водоносным горизонтом, а также непосредственно из этих глинистых слоев /25 , 26 , 40/. Для учета указанных факторов откачка должна иметь достаточно большую продолжительность.
Для большинства песчано-глинистых пород коэффициент пьеэопроводносги заметно зависит от знака нагрузки. Это следует учитывать при анализе результатов откачки, полученных по кривой восстановления уровня.
10
1.4. Некоторые дополнительные фильтрационные параметры
1.4.1. Параметры перетекания характеризуют взаимосвязь водоносных горизонтов, разделенных слабопроницаемым слоем, а также упругие запасы последнего, и входят в расчетные зависимости, учитывающие 'перетекание'. Параметры перетекания имеет смысл определять лишь в тех случаях, когда оценочный расчет, проведенный по данным предварительной разведки, или первых этапов детальной разведки, или лабораторных определений коэффициентов фильтрации глинистых пород, дает основание предполагать широкое развитие процессов 'перетекания' при вскрытии месторождения. Однако для надежного определения этих расчетных параметров откачка должна иметь достаточно большую продолжительность. Кроме того, необходимо исключить перетекание через скважины, попадающие в зону влияния откачки.
Для характеристики гидравлической взаимосвязи водоносных горизонтов в фильтрационных расчетах используется два показателя: параметр 'неусгановившегося перетекания'
о ^0
р- —-——* и параметр установившегося перетекания
TTVQlnr
5* , называемый иногда коэффициентом связиХХ
тtVq * Кг * тTV
( и yrv0- коэффициент фильтрации и мощность слабопроницаемых пород; k , fw и fj/* - коэффициент фильтрации, мощность и упругая водоотдача водоносных пород).
1.4.2. Сопротивление ложа реки (водоема) принято характеризовать расчетным параметром А1/ , определяемым из уел о-вия, что участок длиной Д I/ в рассматриваемом водоносном слое (гидравлически связанном с рекой) будет эквивалентен
в фильтрационном отношении породам, образующим ложе реки (на единицу ширины фильтрационного потока). Этот параметр целесообразно определять в тех случаях, когда в предполагаемую зону влияния водопонижения попадает река (водоем), отделенная от рассматриваемого горизонта грунтовых вод комплексом относительно слабопроницаемых пород.
х Лабораторные испытания не учитывают возможного влия ния трещиноватости глинистых пород на их проницаемость.
** Некоторые авторы используют обратную величину, называя ее также коэффициентом связи.
11
2. ОСНОВНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ФИЛЬТРАЦИИ И ИХ РЕШЕНИЯ В СВЯЗИ С ОПРЕДЕЛЕНИЕМ ФИЛЬТРАЦИОННЫХ ПАРАМЕТРОВ
В настоящей главе дается краткая сводка дифференциаль— ных уравнений, описывающих процесс фильтрации подземных вод для наиболее характерных схем строения водоносной толщи, а также приводятся их простейшие аналитические решения и анализируются возможности использования этих решений для определения фильтрационных параметров.
2.1, Исходные дифференциальные уравнения фильтрации
2.1.1. Основное уравнение двухмерного планового потока имеет вид /43/
а эн а ан ан W(т эг> + тг (т эГ} = р ТГ •
(2.1)
где Т ( X . у . t ) “ проводимость пласта, Н ( X , у . I ) ~ напор, j// - водоотдача, # и 'у - пространственные координаты, t - время.
Для решения практических задач уравнение (2.1) чаще всего линеаризуется путем осреднения Т ( X , у , t ) по пространству и по времени и представляется в виде
а (
а2н
1х*
+
агн . _ а н 9у2 * at
(2.2)
где СЬ= - коэффициент пьезопроводности.
г
Полагая Н =* Н0 ~ S (Но - некоторый исходный напор
в момент t=0, a S * ( Я , у , t ) ~ понижение), уравнения (2.1) и (2.2) можно записать относительно понижения; если в момент % = 0 движение считать стационарным, то уравнения для S идентичны (2.1) и (2.2).
Для одномерного плоскопараллельного потока уравнение (2.2), записанное в понижениях, имеет вид
дг s as л = ТГ ■ (2-3)
для осесимметричного движения ( v “ радиальная координата)
. azs 1 as asм дгг + f Зг at
(2.4)
Для условий установившейся фильтрации последнее уравнение принимает вид
Э2 s 1_ _3S Эг
(2.5)
9 v 2 **
2.1.2. Уравнения (2.1) - (2.5) предполагают, что движение подземных вод во всех точках фильтрующей среды носит плановый характер, г.е. составляющими скорости фильтрации, нормальными водоупорному основанию потока, можно пренебречь. Такое предположение остается в силе при сравнительно малых изменениях проницаемости пород по поперечному сечению потока. При больших различиях в проницаемости вводится предпосылка, что в относительно слабопроницаемых слоях траектории движения нормальны напластованию, а в более проницаемых - параллельны ему. Тогда для частного случая движения подземных вод в двух водоносных горизонтах, разделенных слабопроницаемым слоем, справедлива система уравнений /11, 43, 47/
9Si_ j__д дs^
г дг ' a v
а.
at
+ ISlO.
Т1
as
az
х=о;
(2.6)
J_ _0So. = fl2S0
at dzz
аг
5 Зг__j__d_
at ~ r 9r
( r
asi
TT>
bo
T2
a So
dz
(2.8)
Z=trvfl,
где S-| j OU-| * T1 — понижение, коэффициент пьезопроводности и проводимость опробуемого горизонта; S2 » 01/2* ^2 " то же, для взаимодействующего горизонта; $0 , О^о , "
понижение, коэффициент пьезопроводности1, коэффициент фильтрации и мощность разделяющего слоя, % - вертикальная координата, отсчитываемая от границы опробуемого горизонта и слабопроницаемого слоя. Если в результате относительно высокой проводимости и обеспеченного питания уровни во втором (взаимодействующем) горизонте можно принять постоянными, (не зависящими от перетекания), го из системы исключается уравнение (2.8). Для случая, когда режим фильтрации в разделяющем слое можно считать жестким, из системы выпадает уравнение (2.7).
Аналогом системы (2.6) - (2.8) для условий безнапорной фильтрации в двухслойной среде, состоящей из нижнего (более проницаемого) и верхнего (слабопроницаемого) слоев, является система /11, 43/
т , э2н . _l а н, а н joo ъ- н
I** dr2 г dr ' jj/*
(2.9)
13
- ^ It-1*°i3Trfcl • (2-10)
где И- мощность потока в верхнем слое; Н - напор в нижнем слое, отсчитанный от его кровли; Т и ^И/*- проводимость и упругая водоотдача нижнего слоя; krp и р0- коэффициент фильтрации и водоотдача верхнего слоя.
2* 1,3. При не ус тан овившейся фильтрации к несовершенной по степени вскрытия скважине движение не может считаться плановом; уравнение этого движения для случая однородной изотропной толщи можно представить в виде /47/
(2.11)
дг$ 1 as azs 1 as
dr2 + V 0f + a %z ~ OU di '
2,2. Гидродинамическая типизация пластов, граничные и начальные условия фильтрации
2.2,1* По форм? области фильтрации в плане выделяют следующие типы водоносных пластов;
- неограниченный пласт, который характеризуется весьма большими размерами и такой удаленностью границ, что они не оказывают влияния на процесс фильтрации в рассматриваемой области;
- пол у ограниченный пцаст, имеющий одну прямолинейную границу;
- полосообразный пласт, ограниченный двумя прямолинейными параллельными контурами, имеющими неограниченную протяженность;
- пласт-квадрант, ограниченный двумя прямолинейными контурами, пересекающимися под прямым углом;
- круговой пласт, ограниченный непрерывным круговым контуром.
Перечисленные формы границ области фильтрации (при условии, что они остаются неизменными во времени), отвечают так называемым типовым расчетным схемам, а все прочие -сложным. Пцаст относится к тому или иному типу в зависимости от того, насколько его границы влияют на условия работы дренажного устройства, рассматриваемого в каждой конкретной задаче. Критерием степени такого влияния может служить параметр Фурье . где а - пьезопроводность
'г *
пласта, ъ - время откачки, t* — расстояние до границы пласта. Пласт можно считать неограниченным до тех пор, пока
и* < 0,2.
2*2.2, На границах пласта может иметь место одно из следующих условий:
- условие 1 рода - зависимость напора Н от координат точек границы и времени Нг *■ f i ( ^ г, 7 г, t ) или, в частном случае. Hr - COTvSt •
- условие П рода - зависимость удельного расхода С[ от координат точек границы и времени °[г ж fг (^ г, У г, t ) или, в частном случае, Яг * COHSt;
- условие Ш рода - линейная зависимость между удельным расходом и напором С[ = АН + В, где А и В - посте» явные величины;
- условие 1У рода - равенство напоров и расходов с обеих сторон от границы*
2.2.3. Начальное условие обычно задается распределением естественных напоров H# * f (х , у ), в частном случае, горизонтального начального уровня Н$ =C0*vst .
2.3. Простейшие аналитические решения установившейся фильтрации, используемые для определения фильтрационных параметров
В настоящем параграфе рассмагриваюгея лишь те решения, которые наиболее часто используются на практике для определения фильтрационных параметров. Наибольший интерес представляют решения одномерных - осесимметричных и плос-копараллельных задач.
2.3.1. Простейшие решения для установившейся фильтрации к скважине. Решение уравнения (2.5) для скважины в центре кругового пласта с заданным уровнем на границе можно представить в энде
S( ** ) = IT , (2.12)
где S ( v ) - понижение уровня в точке, расположенной на расстоянии г от опытной скважины; GI - дебит скважины;
Т - проводимость горизонта; R - радиус кругового пласта.
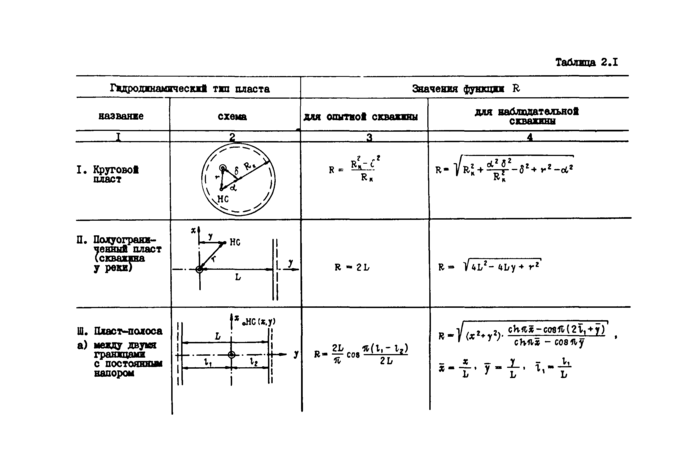
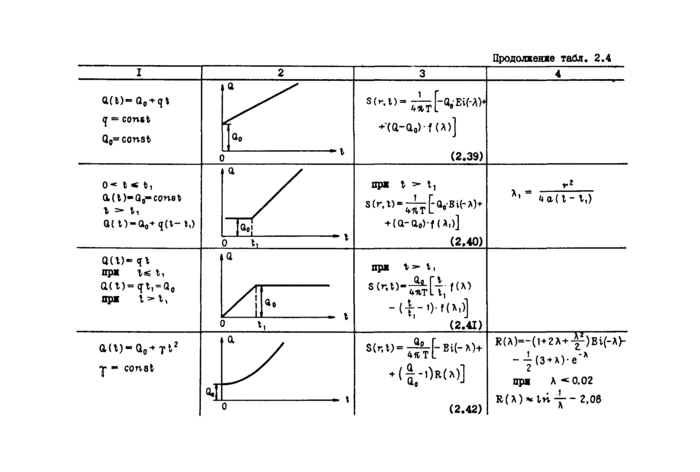
Формулу (2.12) можно использовать для расчета в других типовых (п. 2*2.1) схемах, если понимать под ^ некоторую расчетную функцию, определяемую геометрией области фильтрации. Значения & для наиболее часто встречающихся типовых схем приведены в табл.2.1 /15/.
Кроме приведенных в таблице случаев, установившийся режим фильтрации при откачке може# наступить при подпитывании опробуемого горизонта по площади за счет перетекания когда уровень во взаимодействующем горизонте остается неизменным.
15
|
Таблица 2.1 | ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
б) между об-* ласты) питания и непроницаемой границей
1У. Пласт-квадрант
а)
при двух границах с постоянным напором
|
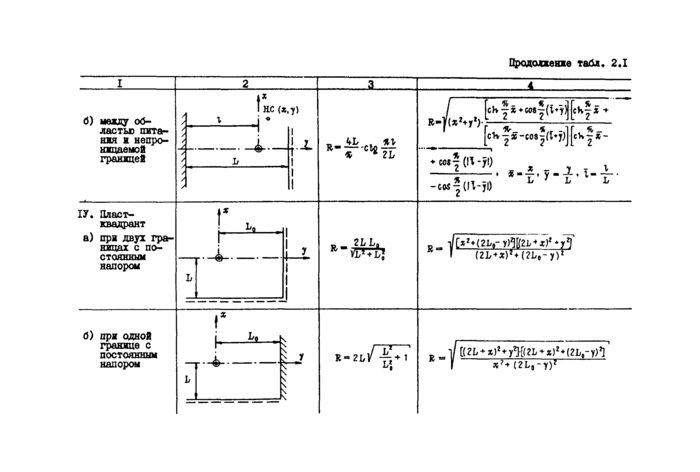
Црододхение табл. 2.1 | |
|
L | |
б) при одной границе с постоянным напором
2ь/
1/ [(2Ь + *)г+уг][(гЬ + *)г + (2Ь0-у>4 Г (2Ь„-у)г
Если водоносный горизонт не ограничен в плане, а уровень взаимодействующего горизонта можно считать горизонтальны^ го понижение S , полученное предельным переходом (при \-**■ —) из решения системы (2.6) - (2.8), определяется выражением /39/
S = 2^ТК0 ’ (2ЛЗ>
где к0 ( 20 ) - функция Бесселя второго рода нулевого порядка (см. приложения 1 и 10), параметр установившегося
перетекания (п. 1.4.1).
ПригУ^^0,05 уравнение (2.13) для практических целей может быть аппроксимировано в виде
S =
а
2ЛТ
Vn'
1.123
t-VT
(2.14)
Это выражение аналогично формуле (2.Г2), если считать, чго .
Если предпосылка о горизонтальном уровне в питающем слое не применима, но можно допустить, чго в питающем слое имеет место установившийся осесимметричный поток с расходом &* , го распределение напоров в рассматриваемом горизонте определяется соотношением /22/
Н - Н* * (НЬ - н?) . (2.1.)
н*~ и*о + -^FVyb~^ • <2-18)
н* -
напоры в питающем слое на контуре стока
где
при г - rQ и в расчетной точке на расстоянии г ; знак*указывает на принадлежности параметра питающему горизонту. Расход на контуре стока (в скважине) определяется выражением
Q= 2%Т
а*
2 «гг
- (н0 -
Ня)
(2.17)
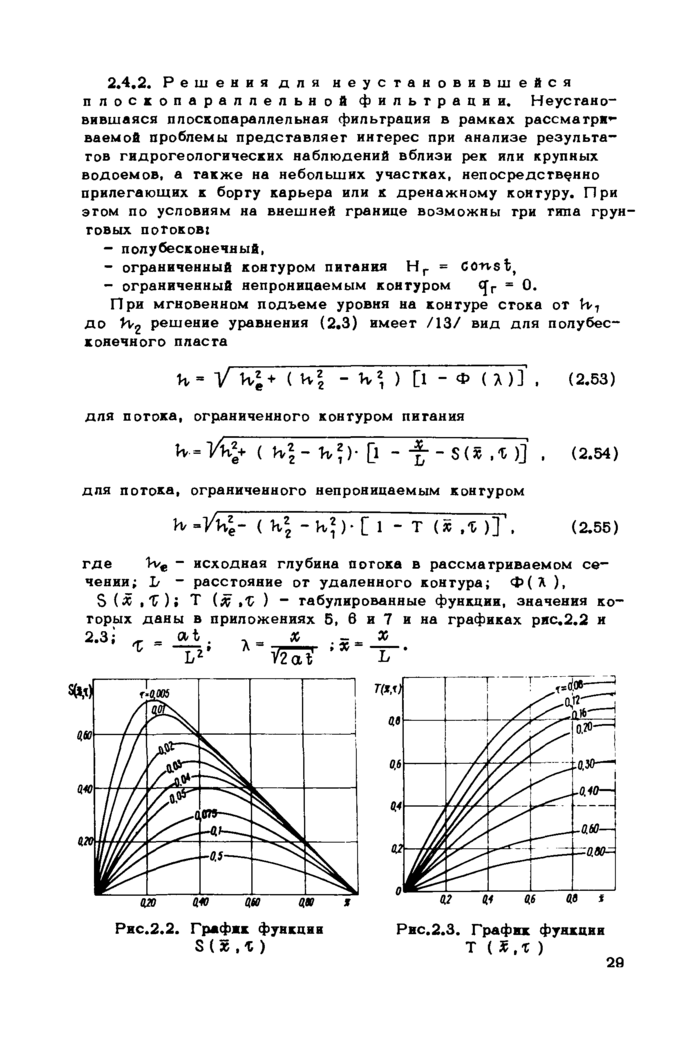
2.3.2. Решения для устаповившейся плоскопараллельной фильтрации. Установившаяся плоскопараллельная фильтрация возможна при наличии контура обеспеченного питания (Н =cotvSfc) или при питании рассматриваемого водоносного горизонта за счет перетекания из более водообильного горизонта, распределение напоров в котором не меняется во времени.
Распределение напоров и удельный расход потока при плос-копараллельной фильтрации в изолированном водоносном горизонте определяются выражениями /35/ при безнапорном режиме
(2.18)
<T
1c- •
Я, - Vyg
2 V
при напорном режиме
Н ( Ж ) - Н0 + \ (Н1 - н0) ,
(2.19)
<т =
т Н1 - Но
г
где /К1 и Ь/0 (Н^ и Н0) - мощность водоносного горизонта (напор) на контуре питания и контуре стока, Ь - расстояние от контура стока до контура питания.
При питании водоносного горизонта за счет перетекания из соседнего горизонта, уровень в котором можно считать горизонтальным, понижение и расход определяются формулами
/22/
S ( X ) - S0
-хУ£
(2.20)
Of - т- So/? . (2.21)
|
Если напор Н* во взаимодействующем горизонте зависит от X линейно, то | ||||
|
2.4. Основные решения неустановившейся фильтрации, используемые для определения фильтрационных параметров
2.4.1. Н еустановившаяся фильтрация к скважине в изолированном водоносном горизонте. Зависимости, наиболее часто используемые для определения фильтрационных параметров при неусгановив-шемся режиме, получаются из решения уравнения (2.4) для неограниченного в плане водоносного горизонта при постоянном расходе опытной скважины. Эго решение выражается известной формулой Тейса
S( г . * > = -jtr t Ei (“ "Ьг)] • (2*24>
4at
19
Методические указания по определению гидрогеологических параметров при разведке и освоении угольных месторождений. Л., 1974. (М-во угольной пром-сги СССР, Всесоюзный науч.-исслед. ин-г горной геомеханики и маркшейдерского дела ГВНИМИ")
В Методических указаниях изложена методика определения основных фильтрационных параметров водоносных горизонтов по результатам опытных откачек и гидрогеологических наблюдений за режи -мом подземных вод.
Работа рассмотрена и одобрена Ученым советом ВНИМИ, Геологическим управлением Мин-углепрома СССР и рекомендована к применению на предприятиях угольной промышленности.
Ил. 23, табл* 21, библиогр. 47, прилож. 11.
(о) Всесоюзный научно-исследовательский институт горной геомеханики и маркшейдерского дела (ВНИМИ), 1974.
где - Е V ( X ) “ интегральная показательная функция, значения которой приведены в приложении 2. Для малых значений аргумента — формулу (2*24) можно аппроксимировать в виде
оЛ
S = In . (2.25)
4И> Т
Сделаем некоторые замечания относительно критерия применимости формулы (2.25), Можно принимать разные значения этого критерия в зависимости от требуемой точности приближения. Для характеристики точности введем коэффициент ф ( г0 ), равный
$ - S пр
<{> ( *о ) - -s-’ 100%' ,
где S и Snp “ истинная и приближенная величины понижения в точке П , определенные, соответственно, по формулам
(2.24) и (2.25); - радиус зоны применимости формулы
(2.25) с точностью ф ( г0 ) процентов в момент Ь . Для различных величин получим следующие значения (го )•
at г
|
При 1 ^0,4 относи- | ||||||||||||||
| ||||||||||||||
|
мендовать к использованию при г -=■ 0,6 |
Формально выражение (2.25) можно привести к виду, аналогичному формуле (2.12), если допустить, что
R = У 2)25 at' . (2.26)
На этом основании иногда вводится понятие 'условного' или 'неустановившегося' радиуса влияния, которому нередко придается не свойственный ему физический смысл.
В настоящей работе условный или неустановившийся радиус влияния понимается как расчетный параметр, который определяется конкретной расчетной схемой фильтрации и аппроксимирующей формулой, принимаемой для описания процесса. Размеры зоны, в пределах которой отмечаются существенные понижения, т.е. формируются основные эксплуатационные запасы, с расчетным радиусом влияния непосредственно отождествляться не могут. Они определяются коэффициентами <pw и Cpq
г 2
= WjJlI = . _ e
г w W общ
4 at
4 at
Et (
4al
>.
ВВЕДЕНИЕ
Фильтрационные параметры водоносных горизонтов, выделяемых в гидрогеологическом разрезе месторождения , являются основным исходным материалом для расчетного обоснования проекта осушения* В сочетании со сведениями о гидрогеологическом строении месторождения и о заданной степени его осушения величины фильтрационных параметров определяют объем и характер дренажных мероприятий, а, следовательно, и суммы материальных затрат на осушение месторождения в целом*
Анализ осушения многих месторождений показывает, что расчетные величины фильтрационных параметров, принятые при обосновании проектов осушения, зачастую существенно (на десятки процентов, а иногда и в несколько раз) отличаются от их действительных значений, причем в одних случаях они оказываются выше, а в других - ниже действительных* Соответственно, мощность первоначально запроектированных дренажных систем оказывается либо неоправданно завышенной, либо недостаточной для обеспечения нормальных условий ведения горных работ, В обоих Случаях это приводит к непроизводительным затратам. Поэтому можно утверждать, что повышение надежности определения фильтрационных параметров является одной из основных проблем, от решения которых зависит рост гехни-ко-экономической эффективности осушения месторождений. Известно, например, что применение электронно-вычислительной и аналоговой техники позволяет довести точность решения прямых гидрогеологических задач (определение притоков, прогноз режима осушения и т,п.) до 2-3%, в то время как при определении исходных параметров, используемых для этих расчетов, считаются вполне допустимыми ошибки в 2О“30%. Более того, оценить заранее точность полученных параметров вообще пока не представляется возможным*
Проблема изучения фильтрационных свойств горных пород обычно рассматривается как практическое приложение общей теории фильтрации в пористых средах. Между тем, исследования последнего периода показали со всей очевидностью, что обоснованная интерпретация опытно—фильтрационных работ нередко требует применения специального теоретического анализа, учитывающего ряд дополнительных осложняющих факторов. Иначе говоря, и в теоретическом плане данная проблема приобретает вполне самостоятельное значение.
Основную трудность в проблеме определения фильтрационных параметров на сегодня представляет вопрос о соответствии действительных гидрогеологических условий выбранной
3
расчетной схеме фильтрации. Поэтому особая роль в работе отводится методам качественной интерпретации исходных экспериментальных данных, а также анализу совокупности значений фильтрационных параметров. По той же причине большое внимание уделяется гем методам, которые в гой или иной мере учитывают возможное разнообразие граничных условий (или 'нейтрализуют* их нерпределейность). Таковы, в частности, интегральные и аналоговые методы, позволяющие использовать одновременно большой объем информации, полученной при проведении эксперимента.
В работе уделено внимание и вопросам систематизации представлений о методах определения фильтрационных параметров. Дело в том, что результаты исследований по данной проблеме, как правило, публикуются в виде отдельных сообщений в различных периодических изданиях и нередко только в силу этого не находят должного практического применения.
В го же время в вышедших в последние годы работах методического и справочного характера, как правило, дается большой набор отдельных расчетных зависимостей и приемов без пояснений их методологической основы, а иногда и без достаточного анализа условий их применимости. Поэтому в практике гидрогеологических исследований чаще всего используются наиболее простые методические приемы, нередко совершенно не отвечающие ни современным представлениям о движении подземных вод, ни конкретным условиям фильтрации.
Основное внимание в 'Методических указаниях...' уделяется методике обработки результатов опытных откачек - наиболее важного вида опытно-фильтрационных работ в практике гидрогеологических исследований для цепей осушения. Известно, однако, что вследствие кратковременности и относительно небольшой производительности опытных откачек, их результаты характеризуют лишь некоторую ограниченную площадь области фильтрации, в го время как для решения вопросов осушения месторождений необходимо знать свойства водоносных горизонтов на всей площади их распространения. Кроме того, в особо сложных гидрогеологических условиях -надежное определение фильтрационных параметров по результатам опытных откачек нередко вообще не представляется возможным. Поэтому, наряду с обработкой результатов опытных откачек, рассматривается методика интерпретации результатов гидрогеологических наблюдений, проводимых в процессе опытно-эксплуатационного водопонижения и на первых стадиях осушения месторождения.
'Методические указания...' составлены канд.геол.-мия. наук Л*И.Сердюковым. Раздел 1 н подразделы 3.1, 3.7 и 5.1 составлены с участием доктора геол.-мин. наук, проф. В.А.Ми-
4
роненко, а подраздел 5.3 составлен канд.геол.-мин.наук Ю.А.Норваговым»
Возможные критические замечания и предложения по рабо-те будут приняты авторами с вниманием и признательностью»
1. КРАТКАЯ ХАРАКТЕРИСТИКА ОСНОВНЫХ ФИЛЬТРАЦИОННЫХ ПАРАМЕТРОВ
Фильтрационные свойства пород и водоносных горизонтов в целом характеризуются следующими параметрами: коэффициентом фильтрации ( % ) или проводимостью (Т), водоот
дачей ( [ju ), упругой водоотдачей ( JA/*), коэффициентами уровнепроводности ( а ) и пьезопроводносги ( ои*), параметрами перетекания ( \ и fi ) и параметром, характери
зующим сопротивление ложа реки или водоема ( Д1/ ).
1.1. Коэффициент фильтрации и проводимость
1.1.1. Коэффициент фильтрации характеризует величину сил сопротивления, препятствующих движению воды в горной породе; он отражает влияние физических свойств породы, слагающей водоносный горизонт, и самой воды, заключенной в этой породе, на процесс фильтрации. В однородных раздел ьно-зернистых и мягких связных породах величина коэффициента фильтрации определяется, в первую очередь, их активной пористостью; в твердых горных породах величина коэффициента фильтрации определяется трещиноватостью и активной пористостью^ причем во многих случаях роль трещиноватости является определяющей.
Так как при снижении гидростатического напора эффективные напряжения возрастают и пористость (степень трещиноватости) породы уменьшается, то коэффициент фильтрации при осушении должен снижаться, хотя в большинстве случа--ев этими изменениями можно пренебречь. Зависимость коэффициента фильтрации от давления должна учитываться, по меньшей мере, в следующих случаях:
а) при осушении, когда вблизи депрессионной поверхности безнапорного горизонта образуется зона неполного насыщения, в пределах которой, согласно С.Ф.Аверьянову /1/, эффективный коэффициент фильтрации
у = Ъ / WJLWм
v ' w - WM ' ’ ’
где и W0 - коэффициент фильтрации и влажность при
полном насыщении, "W - действительная влажность, -влажность, при которой перемещение влаги практически отсутствует;
б) при нагнетаниях в трещиноватые породы, когда давление нагнетания соизмеримо с Фи ( - объемный вес
пород, Фи - глубина нагнетания), изменение коэффициента фильтрации вследствие раскрытия трещин может достигать десятков и даже сотен процентов.
Весьма существенными могут оказаться также изменения коэффициента фильтрации, вызываемые копьматацией или суффозией /30/.
1,1.2. Как константа закона Дарси коэффициент фильтрации является характеристикой, статистически осредненной по плошади поперечного сечения потока, С позиций механики сплошной среды, минимальный размер площади, для которой определяется коэффициент фильтрации, должен превышать размеры блоков или зерен фильтрующего массива более чем в 7-10 раз /32/. Эго обстоятельство особенно важно учитывать при исследовании проницаемости массивов твердых пород, разбитых редкими тектоническими трещинами большой протяженности. В связи с этим следует отметить, что расход потока (а следовательно, и расчетный коэффициент фильтрации) зависит, в основном, от числа и расположения именно крупных трещин, так как расход пропорционален третьей степени величины раскрытия трещины /3/.
1Л.З. В закарсгованных породах величины коэффициентов фильтрации, получаемые в результате опытных работ, являются наиболее условными. Проницаемость карстового массива определяется, главным образом, пропускной способностью наиболее крупных каналов, поэтому рассчитанные по результатам опытов величины коэффициента фильтрации 6yayt резко меняться в зависимости от того, насколько близко расположена опытная скважина к одному из таких каналов. Интерпретация опыта существенно осложняется еще и тем, что фильтрация в крупных каналах подчиняется законам трубной гидрав~ лики. Наконец, иногда коэффициент фильтрации может меняться в процессе откачки в результате перемещения заполнителя карстовых каналов и пусто г. По этим причинам оценка проницаемости закарсгованных пород обычно может быть достаточно надежной лишь в результате проведения опытных откачек, близких по своим условиям к эксплуатационным.
1.1.4. В глинистых слабофильгрующих породах коэффициент фильтрации особенно важно устанавливать для оценки связи водоносных горизонтов между собой и с возможными источниками питания (за счет поверхностных и атмосферных вод). При этом проницаемость плотных глин, разделяющих глубокие водоносные горизонты, определяется, в значительной мере, их трещиноватостью, а проницаемость покровных отложений зоны аэрации зависит от их влажности (п. 1.1.1).
1.1.5. Наряду с коэффициентом фильтрации, для суммарной характеристики водопроницаемости толщи пород используется проводимость (Т =■ 1с*уь), представляющая собой произведение среднего коэффициента фильтрации рассматриваемого горизонта (по напластованию) на его мощность. При практическом использовании этот» показатель зачастую оказывается
7-
более удобным» чем коэффициент фильтрации» так как он мо" жет определяться в полевых условиях без детального изучения мощности отдельных слоев рассматриваемой толщи.
1.2. Водоотдача и упругая водоотдача
1.2.1. Водоотдача ( \А/ ) - основной параметр, характеризующий статические запасы подземных вод в условиях безнапорной фильтрации. Водоотдача представляет собой отношение объема воды, вытекающей под действием силы тяжести из некоторого объема полностью водонасыщенного грунта, ко всему этому объему. Как параметр уравнения Буссинеска, описывающего процесс фильтрации подземных вод в безнапорных горизонтах, водоотдача считается величиной постоянной. Однако исследованиями ряда авторов /28, 36, 45, 46/ показано, что водоотдача является величиной, зависящей от времени дренирования и скорости снижения уровня: после снижения уровня безнапорного водоносного горизонта над депрессионной кривой в
породе остается часть гравитационной воды, процесс стекания которой растягивается во времени. Аналогичное явление может возникнуть в трещиноватых и, особенно, закарстованных породах: наиболее быстро здесь отдают воду крупные трещины илн каналы, а отекание воды из более мелких трещин или каналов отстает во времени. Более того, иногда вода может вообще 'консервироваться* в отдельных тупиковых каналах. Отсюда следует, что для правильного определения водоотдачи продолжительность опыта не должна быть слишком малой.
1.2.2. Ориентировочные значения водоотдачи для песчаногравийных отложений можно принимать по табличным данным /36/. Для твердых пород водоотдача определяется, в основном, трещиноватостью (кавернозностью), хотя для некоторых пород (например, песчаников) большое значение имеет вода, заключенная в порах. Обычно величина водоотдачи трещиноватых твердых пород не превышает 0,01 , но для некоторых сильно закарстованных карбонатных пород и для интенсивно трещиноватых углей она может достигать 0,03-0,05 и даже 0,1. Породы супесчаного и суглинистого составов, нередко клаосифипируемые по проницаемости как относительный водо-упор, могут содержать большие запасы воды, частично срабатываемые при откачке. Это должно учитываться при производстве опытов и обработке их результатов. В частности, именно поступлением воды из 'водоупорных' слоев часто объясняется быстрое достижение ложностационарного режима фильтрации при опытных откачках в безнапорных водоносных горизонтах двухслойного строения /26, 40/.
8
1.2.3* Для характеристики упругих запасов напорных водоносных горизонтов используется коэффициент упругой водоотдачи (или просто упругая водоотдача fA/* ). Снижение гидростатического напора в процессе дренирования напорного горизонта приводит к увеличению сжимающих напряжений в скелете грунта. Под действием этой дополнительной ('депрессион-ной') нагрузки водоносный горизонт сжимается с соответствующим уменьшением объема порового пространства. Одновременно с этим происходит упругое расширение самой воды. В результате, из каждой единицы объема пласта выделяется некоторый объем воды
ЛТГ = Л Н (rv[3B + |3п ), (1.1)
где ДН - изменение гидростатического напора; w - пористость; |Зви Рп “ коэффициенты объемной упругости воды и породы.
Количество воды, выделяемое единицей объема пласта при снижении напора на 1 м, называется коэффициентом упругоем-косги пласта ( В*)
о* AV
1 дн =>vpB+Рл • (1,2)
Коэффициент упругой водоотдачи представляет собой объем воды, выделяемой единицей площади пласта при снижении напора на 1 м, т.е.
^*=trv|3* (1.3)
1.2.4. Упругая водоотдача песчаных и многих твердых пород оказывается обычно на несколько порядков ниже, чем величина гравитационной водоотдачи. Однако твердые породы с высокой пористостью (например, мел ) могут отдавать большие объемы воды в процессе сжатия под возникающими при откачке депрессионными нагрузками /4, 25/, так что результирующая величина водоотдачи может значительно превышать величину водоотдачи, обусловленную трещиноватостью указанных пород.
В глинистых породах упругая водоотдача может измеряться величинами, превышающими на несколько порядков упругую водоотдачу водоносных пород.
1.2.5. Водоотдача и упругая водоотдача как фильтрационные параметры непосредственно в фильтрационных расчетах используются относительно редко. Чаще они входят в состав обобщенных параметров - коэффициентов уровнепроводности и
п ьез оп р ов од н ос ги.
9