ГОСТ 23603-79
Надежность в технике. Статистическая оценка нагруженности машин и механизмов. Методы выбора условий проведения испытаний
Купить ГОСТ 23603-79 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Устанавливает методы выбора условий проведения испытаний машин и механизмов с целью получения статистической информации для оценки нагруженности и характеристик надежности в процессе функционирования или при имитации условий эксплуатации. На основании стандарта допускается разрабатывать отраслевую нормативно-техническую документацию, отражающую специфику испытаний.
Переиздание (ноябрь 1980 г.)
Отменен без замены, действует методический документ.
Оглавление
1 Общие положения
2 Методы выбора условий проведения испытаний
3 Процедура условий проведения испытаний
Приложение 1 (рекомендуемое) Термины, применяемые в стандарте, и их определения
Приложение 2 (справочное) Пример выбора условий проведения испытаний методом с использованием активной стратегии эксперимента при определении нагруженности электропогрузчика
| Дата введения | 01.01.1980 |
|---|---|
| Добавлен в базу | 01.02.2017 |
| Завершение срока действия | 01.07.1986 |
| Актуализация | 01.01.2021 |
Организации:
| 26.04.1979 | Утвержден | Государственный комитет СССР по стандартам | 1570 |
|---|---|---|---|
| Издан | Издательство стандартов | 1982 г. |
Reliability in technique. Estimator of the loading of machines and mechanisms. Methods of selection of test conditions
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8
стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
НАДЕЖНОСТЬ В ТЕХНИКЕ
СТАТИСТИЧЕСКАЯ ОЦЕНКА НАГРУЖЕННОСТИ МАШИН И МЕХАНИЗМОВ
МЕТОДЫ ВЫБОРА УСЛОВИЙ ПРОВЕДЕНИЯ ИСПЫТАНИЙ
Цена I коп.
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ М о с к ■ а
УДК 421-192 : 066.354 Группа Т51
Г О С У Д А Р С Т в Е Й Н Ы Й СТАНДАРТ СОЮЗА ССР
Надежность а технике
ГОСТ
23603-79
СТАТИСТИЧЕСКАЯ ОЦЕНКА НАГРУЖЕННОСТИ МАШИН И МЕХАНИЗМОВ Методы выбора условий проведения испытаний
Reliability in technique. Estimator of the loading of machines and mechanisms. A)ethods of selection of test conditions
Постановлением Государственного комитета СССР по стандартам от 26 апреля 1979 г. № 1570 срок введения установлен
с 01.01 1980 г.
Настоящий стандарт устанавливает методы выбора условий проведения испытаний машин и механизмов с целью получения статистической информации для оценки нагруженности и характеристик надежности в процессе функционирования или при имитации условий эксплуатации. На основании настоящего стандарта допускается разрабатывать отраслевую нормативно-техническую документацию, отражающую специфику испытаний.
Термины, применяемые в стандарте, и их определения приведены в рекомендуемом приложении 1.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Выбор условий проведения испытаний машин и механизмов заключается в определении уровней и сочетании факторов, относящихся к внешним воздействиям и условиям применения машин и механизмов, значимо влияющих на статистические характеристики нагруженности и надежности.
1.2. Выбор конкретных факторов, при воздействии которых должны проводиться испытания, определяется целями и задачами испытаний и основывается на данных о предполагаемых условиях эксплуатации.
Издание официальное ★
1.3. Выбор основных уровней факторов должен осуществляться на базе статистических данных о режимах функционирования и
Перепечатка воспрещена
Переиздание. Ноябрь 1980 г.
© Издательство стандартов, 1982
Стр. 10 ГОСТ 23603-79
ность зависят от свойств выборки и нуждаются в статистическом анализе. Регрессионный анализ, как и всякий статистический метод, применим при определенных постулатах:
1. При всяком X исследуемый параметр У есть случайная величина с нормальном законом распределения и дисперсия воспроизводимости — одна из характеристик этого закона. (Этот постулат выполняется, принимая во внимание априорную информацию).
2. Дисперсия S(r) не зависит от абсолютной величины Y.
3. Установление каждого фактора на заданный уровень и его поддержание существенно точнее ошибки воспроизводимости. (Выполняется).
4. Факторы можно изменять независимо. (Выполняется).
Итак, постулаты 1, 3, 4 выполняются. Остается проверить второй постулат об однородности дисперсий.
Нели сравниваемое число дисперсии больше двух, то для проверки однородности дисперсий можно воспользоваться критерием Кохрена. Этот критерий пригоден, если во всех точках эксперимента имеется одинаковое число повторных опытов. При этом вычисляют дисперсию в каждой горизонтальной строке матрицы результатов эксперимента (табл. 3) по формуле
2 (У.д-У,)2
с 2 = 1_
1 п— 1
где Ущ — результат отдельного опыта в i-ой строке; п — число повторных опытов.
Затем из всех дисперсий находится наибольшая и делится на сумму всех дисперсий:
Smax 0,000392 N 2 “ 0,002306"" 0,1'•
2 о.-
|
Таблица 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 0,002306 |
ГОСТ 23603-79 Стр. 11
Для нашего случая (Лг=8, п = 2, а = 0.05) табличное значение критерия Кохрсна
^табл = 0,68.
Таким образом G<Gr*6n и гипотеза об однородности дисперсий Принимается.
Теперь можно усреднять дисперсии и найти дисперсию воспроизводимости (среднюю дисперсию эксперимента):
N п —
2 2 (Ki„—У,)2 с 2 1 <7“ I 0,002306 п лллоос
S<r>--лГ(^Т)---8 “а000288'
где 1=1, N; <7=1, я.
8.2. Определение коэффициентов уравнения регрессии.
Назовем разность между результатами опыта и предсказанными по уравнению регрессии значениями отклика невязкой, т. е.
— Л
lV-W-fc.
Будем искать коэффициенты регрессии из условия минимума суммы квадратов невязок
N
U= 2 I* =min.
В таком случае можно показать, что для любого числа факторов коэффи циенты будут определяться по следующей формуле
1 N -
N 7-1 •
где У=0, 1, 2, 3,..., k номер фактора (ноль записан для вычисления (50); Ti — средний отклик в i-ой точке плана.
Так как каждый фактор (кроме Х0) варьирует на двух уровнях (+1 и —1), то вычисления коэффициентов сводятся к приписыванию столбцу У знака, соответствующего фактору столбца и алгебраическому сложению полученных значений. Деление результата на число опытов даст искомый коэффициент.
Для определения оценки эффектов взаимодействий надо, пользуясь правилом перемножения столбцов, получить столбцы произведений двух факторов и столбец произведения трех факторов. При вычислении коэффициента, соответствующего эффекту взаимодействия, с новым вектор-столбцом можно обращаться так же, как и с вектор-столбцом любого фактора.
8 _
2 У,
Ро--^--U94;
2УГ*ц
--—0,121;
2№
02=—!{—-=0,0046;
2Й31
& =-=0,089;
о
Пользуясь табл. 2 произведем вычисления:
2У4Х„Х21 Э.я——!—5-=0,006;
о
2ад,х31
Э,3 = —1—з- 0,006;
8
iZXi iX3l
p23 = -‘—-- 0,021;
8
Рт=----=0.027.
Стр. 12 ГОСТ 23603-79
Таким образом уравнение регрессии имеет вид
У= 1,194—0,121*,+0.0046*2+0,089*3+0,006*|*2+а,006*,*з— —0,021 *2*а+0,027*, вд.
8.3. Проверка значимости коэффициентов и определение окончательного вида уравнения регрессии.
Сначала определим дисперсию оценки коэффициента регрессии:
|
0,000288 16 |
0,000018.
Затем находим доверительный интервал для коэффициента:
где /— табличное значение критерия Стьюдента, при числе степеней свободы /=8, с которым определялось S*Y\ и при выбранном уровне значимости (а = 0,05);
S(p } — среднеквадратическая ошибка коэффициента регрессии.
/=2,31 (/ = 8, а=0,05);
5(Pj) -V0,000018 = 0,0042;
Др1=2 • /. S({Jj) = 2 • 2,31 • 0,0042 = 0,0194.
Коэффициент считается значимым, если его абсолютная величина больше доверительного интервала. Сравнивая доверительный интервал и оценки значений коэффициентов, приходим к выводу, что коэффициенты при *2, а также при *,*2, *,*3 незначимы. Поэтому уравнение регрессии приобретает следующий вид:
У — 1,194—0,121*,+ 0,089*3—0,021 *2*з+0,027*, *2*3.
8.4. Проверка адекватности модели.
Для проверки гипотезы об адекватности модели необходимо сопоставить точность модели с величиной, характеризующей точность наблюдений (опытов). Если ошибки, характеризующие точность модели, превосходят ошибки наблюдений, то гипотеза об адекватности модели отклоняется.
Адекватность можно оценить с помощью дисперсионного отношения:
2
ад
Л/ __ А
п 2 (У,-У,)2
7
где п—число параллельных опытов;
/V—число опытов в матрице плана;
/—число значимых коэффициентов (включая и свободный член ро)-
А
В данном случае для каждой точки плана матрицы находим значения У|,
предсказанные моделью:
л
У, = 1,194+ 0,121—0,089—0,021—0,027=1,178
У2= 1,194—0,121—0,089-0,021 + 0,027=0,990
А
Уз = 1,194+ 0,121 —0,089 + 0,021 + 0,027 = 1,274
ГОСТ 23603-79 Стр. 13
Л
У4 = 1,194—0,121 —0.089 + 0,021—0,027 = 0,978;
Л
У* = 1,194 + 0,121 +0,089 + 0,021 +0,027= 1,452;
Ув«=1,194—0,121 + 0,089+ 0,021 —0,027 =1,156;
У7 -1,194+0,121 + 0,080-0,021—0,027=1,356;
У» =1.194—0,121+ 0,089-0,021 + 0,027 = 1,168,
Пользуясь данными табл. 3, найдем:
N __ л п 2 (У|— У,)2
S2aд - —--0,00047.
I з
Расчетное значение критерия Фишера:
0.00047
рдс,== S*Y)“ 0,000288 “1’w*
Табличное значение критерия Фишера:
/гт*бя = 4,07 (/i = 3, /,= 8. а=0,05).
Модель адекватна, так как
^ расч'С^твва-
Полученный факторный план дает полное представление о том, какими должны быть искомые условия испытании.
Стр. 2 ГОСТ 23603-79
условиях применения машины или механизма. В качестве основных уровней факторов следует принимать такие значения, которым соответствует наибольшая плотность распределения в условиях эксплуатации.
1.4. Планирование эксперимента и выбор условий испытаний должны быть направлены на снижение сроков и объемов испытаний при условии обеспечения заданной точности результатов.
1.5. Правильность выбора условий проведения испытаний и точность результатов должны быть подтверждены критериями математической статистики.
1.6. Пример выбора условий проведения испытания приведен в справочном приложении 2.
2. МЕТОДЫ ВЫБОРА УСЛОВИЙ ПРОВЕДЕНИЯ ИСПЫТАНИЙ
2.1. В зависимости от стратегии сбора экспериментальной информации, необходимой для статистической оценки нагруженности машин и механизмов, существует три метода выбора условий испытаний:
с использованием стратегии активного эксперимента;
с использованием стратегии пассивного эксперимента;
с использованием стратегии смешанного эксперимента.
2.2. При решении задач статистической оценки нагруженности и работоспособности машин и механизмов применяют все три метода выбора условий проведения испытаний.
2.3. Применение методов зависит от возможности целенаправленного изменения уровней факторов и их сочетаний:
метод с использованием стратегии активного эксперимента — при наличии управляемых факторов и отсутствии неуправляемых;
метод с использованием стратегии пассивного эксперимента — при отсутствии управляемых факторов;
метод с использованием стратегии смешанного эксперимента — при наличии управляемых и неуправляемых факторов или использовании части управляемых факторов в виде неуправляемых.
2.4. При накоплении статистических данных об условиях применения и режимах функционирования машин и механизмов применяют метод с использованием стратегии пассивного эксперимента.
3. ПРОЦЕДУРА ВЫБОРА УСЛОВИЙ ПРОВЕДЕНИЯ ИСПЫТАНИЙ
3.1. Выбор условий проведения испытаний состоит из шести этапов.
3.1.1. Определение совокупности качественных и количественных факторов, влияющих на статистические характеристики нагруженности и возникновение отказов. Этап состоит из двух стадий:
ГОСТ 23603-79 Стр. 3
сбор априорной информации и проведение анализа имеющихся теоретических и экспериментальных данных о внешних воздействиях и режимах функционирования в реальных условиях применения машин и механизмов;
установление перечня факторов, оказывающих наиболее существенное влияние на значения статистических характеристик' на-груженности и надежности.
3.1.2. Выдвижение гипотезы о виде функциональной связи между воздействующими факторами, статистическими характеристиками нагруженности и характеристиками надежности.
3.1.2.1. При известном виде функциональной связи или достаточном количестве информации для определения вида этой связи следует пользоваться моделью в виде соответствующего аналитического выражения.
3.1.2.2. Если вид функциональной связи неизвестен, ее представляют при помощи полиномиальной модели, которую строят по результатам натурных испытаний с использованием методов математической статистики.
3.1.2.3. Если несколько моделей обеспечивают необходимую точность оценки статистических характеристик нагруженности, то следует использовать самую простую.
3.1.3. Выявление возможности измерения и целенаправленного изменения значений эксплуатационных факторов в процессе ио пытаний. Этап состоит из стадий:
выделение количественных факторов;
выделение контролируемых, управляемых факторов;
оценка областей определения количественных, управляемых факторов, исходя из реальных условий применения машины или механизма и физических возможностей проведения испытаний.
3.1.4. Определение метода выбора условий проведения испытаний (см. пп. 2.3 и 2.4).
3.1.5. Планирование эксперимента.
3.1.5.1. В случаях стратегии пассивного эксперимента, применяемой для установления функциональной связи между воздействующими факторами и нагруженностью, а также для накопления статистических данных об условиях применения, регистрацию неуправляемых факторов производят без целенаправленного их изменения при функционировании машины или механизма. Планирование эксперимента при этом заключается в организации пассивного сбора информации (выбор интервала времени между моментами регистрации данных, задание объема выборки).
3.1.5.2. В случаях активной стратегии эксперименты проводятся в некотором числе точек факторного пространства (варьирование условий эксперимента), выбираемых по заранее составленному плану (матрица планирования) и учитывающих не только номинальные, но и предельные уровни значений факторов, а также не-
благоприятные их сочетания. Размер интервала варьирования'зависит от конкретной задачи оценки нагруженности и надежности, размера области определения фактора, степени полинома и точности фиксирования фактора, а также точности измерения оцениваемой характеристики.
План эксперимента определяет точность искомой полиномиальной модели и составляется на основе методов теории планирования эксперименту.
3.1.6. Проведение эксперимента с целью оценки адекватности модели связи воздействующих факторов со значениями статистических характеристик надежности и нагруженности состоит из следующих стадий:
проведение эксперимента по выбранному плану; определение параметров модели на основе методов математической статистики;
проверка модели на адекватность.
При адекватности модели следует сделать вывод об окончании эксперимента.
В случаях неадекватности модели следует выбрать модель иного вида, добавить точки в план эксперимента для обеспечения оценки параметров новой модели и провести эксперимент.
ГОСТ 23603-79 Стр. 5
ПРИЛОЖЕНИЕ 1 Рекомендуемое
ТЕРМИНЫ, ПРИМЕНЯЕМЫЕ В СТАНДАРТЕ, И ИХ ОПРЕДЕЛЕНИЯ
|
Термин |
Определение |
|
1. Нагруженность |
Состояние машины или механизма, обусловленное внешними воздействиями, и условиями функционирования |
|
2. Условия испытаний |
Совокупность уровней и сочетаний факторов, относящихся к внешним воздействиям и условиям применения, значимо влияющих на нагруженность машин и механизмов, а также объем, порядок выполнения опытов и интервалы времени между моментами регистрации данных |
|
3. Фактор 4. Значимый фактор |
Контролируемая переменная объекта Контролируемая переменная, значимо влияющая на нагруженность |
|
5. Качественный фактор |
Фактор, которому нельзя поставить в соответствие числовую шкалу и который можно оценить лишь качественно |
|
6. Количественный фактор |
Фактор, который можно оценить количественно при помощи соответствующей его природе шкалы |
|
7. Уровень фактора 8. Кодирование факторов |
Фиксированное значение фактора Переход от натуральных значений факторов к их безразмерным значениям |
|
9. Основной уровень фактора |
Натуральное значение фактора, соответствующее нулю в безразмерной шкале |
|
10. Управляемый фактор |
Фактор, уровень которого можно выбирать и фиксировать по желанию исследователя |
|
11. Неуправляемый фактор |
Фактор, уровень которого не зависит от желания экспериментатора или не управляется им |
|
12. Область определения фактора |
Область изменения уровня фактора, ограниченная техническими возможностями машины, а также возможностями фиксации н измерения в условиях эксперимента |
|
13. Факторное пространство |
Пространство контролируемых переменных |
|
14. Размах варьирования фактора |
Разность между максимальным и минимальным значением фактора в данном плане |
Термин
Определение
15. Интервал варьирования фактора
16. Активный эксперимент
17. Пассивный эксперимент
18. План эксперимента
19. Матрица планирования
20. Точка плана
21. Полный факторный эксперимент
22. Рандомизация
23. Параллельные опыты
24. Дисперсия воспроизводимости
25. Отклик
26. Функция отклика
27. Модель математическая
28. Адекватность модели
29. Модель регрессионного анализа
30. Модель регрессионного анализа линейная по параметрам
31. Полиномиальная модель
32. Коэффициент регрессии
33. Нагружение
Натуральное значение фактора, соответствующее единице в безразмерной шкале Эксперимент, в котором уровни факторов для каждого опыта задаются исследователем
Эксперимент, в котором уровни факторов не зависят от желания экспериментатора или не управляются им и лишь производится их регистрация Правила проведения эксперимента, устанавливающие объем, условия и порядок проведения эксперимента Стандартная форма записи условий проведения экспериментов в виде прямоугольной таблицы, строки которой отвечают опытам, столбцы — факторам Упорядоченная совокупность числовых значений факторов, соответствующая условиям проведения опыта Эксперимент, проводимый по плану, содержащему все возможные комбинации всех факторов на определенном числе уровней равное число раз Случайный порядок проведения опытов Рандомизированные во времени опыты, в которых уровни всех факторов постоянны Дисперсия результатов в параллельных опытах
Зависимая случайная переменная объекта Зависимость математического ожидания отклика от факторов Математическое описание объекта или явления
Соответствие модели экспериментальным данным по заданному критерию с заданной степенью точности Модель, отражающая зависимость математического ожидания отклика от непрерывных контролируемых переменных Модель регрессионного анализа, в которой математическое ожидание отклика есть линейная комбинация базисных функций от факторов
Модель регрессионного анализа линейная по параметрам, задаваемая полиномом по факторам
Параметр модели регрессионного анализа, входящий в модель линейно Процесс, характеризующийся изменением нагруженности во времени
ГОСТ 23603-79 Стр. 7
ПРИЛОЖЕНИЕ 2 Справочное
ПРИМЕР ВЫБОРА УСЛОВИЙ ПРОВЕДЕНИЯ ИСПЫТАНИЙ МЕТОДОМ С ИСПОЛЬЗОВАНИЕМ АКТИВНОЙ СТРАТЕГИИ ЭКСПЕРИМЕНТА ПРИ ОПРЕДЕЛЕНИИ НАГРУЖЕННОСТИ ЭЛЕКТРОПОГРУЗЧИКА
1. Цель и задачи испытаний.
Цель — оценка значимости факторов, определяющих нагруженность электропогрузчика и закон расхода энергии источников питания.
Задача — экспериментальное исследование влияния факторов, определяющих нагруженность и расход энергии электропогрузчика.
2. Перечень факторов, оказывающих наиболее существенное влияние на расход электроэнергии.
По априорным сведениям известно, что на расход электроэнергии (К) погрузчика влияют факторы:
высота подъема груза для укладки в штабель (Xi);
плечо пробега (Х7) \
вес груза (Х3).
3. Выдвижение гипотезы о виде функциональной связи между воздействующими факторами и расходом электроэнергии.
В данном случае ставится интерполяционная задача — установить связь между расходом электроэнергии и тремя факторами в зоне их определения. Выбрать модель — значит выбрать вид этой связи, записать ее уравнение. По результатам эксперимента необходимо оценить численное значение констант (коэффициентов) этого уравнения. Поскольку отсутствует информация о виде и структуре указанной связи, будем аппроксимировать неизвестную нам функцию отклика полиномом. Полный факторный эксперимент типа 23 позволяет получить полиномиальную модель, учитывающую эффекты взаимодействия первого и второго порядков (неполного квадратного уравнения регрессии) вида:
У= Po+Pl^t"bP2^2+P3^T+Pl2^l^2 + ‘Pl3^l^3+ Р23Х2Х3+Pl2S^I^2^i-
Для подсчета коэффициентов этого уравнения составляется матрица (табл. 2).
4. Выявление возможности измерения й целенаправленного изменения значений эксплуатационных факторов в процессе испытаний.
Таблица 1
|
Кодирование факторов | |||||||||||||||||||||||||
| |||||||||||||||||||||||||
|
Все взятые факторы, вли ле на расход электроэнергии, очевидно являются количественными, контролируемыми и управляемыми. Оценка областей определения этих факторов (табл. 1) проводилась на основе статистических |
данных использования погрузчика, его технических характеристик и аппаратурного обеспечения эксперимента.
5. Определение метода выбора условий проведения испытаний.
На основе положений п. 2.3 настоящего стандарта принимается метод с использованием активной стратегии эксперимента.
6. Планирование эксперимента.
В ходе эксперимента предполагалось каждый фактор варьировать на двух уровнях: верхнем и нижнем. Кодовое обозначение верхнего уровня +1, нижнего —1. Значение уровней факторов показано в табл. 1.
В интерполяционных задачах интервалы варьирования факторов должны охватывать всю зону определения этих факторов.
Перевод факторов в кодированные значения осуществляется по формуле
х\—*ю /)
где Xj— кодированное значение фактора;
л:) — натуральное значение фактора;
***
хуо'— натуральное значение нулевого уровня;
/j— интервал варьирования фактора;
/ — номер фактора.
В данном эксперименте были реализованы все возможные сочетания уровней факторов (полный факторный эксперимент — ПФЭ). Если число уровней каждого фактора равно двум, а число факторов равно трем, то число опытов для полного факторного эксперимента определяется по следующему выражению:
N^2\
|
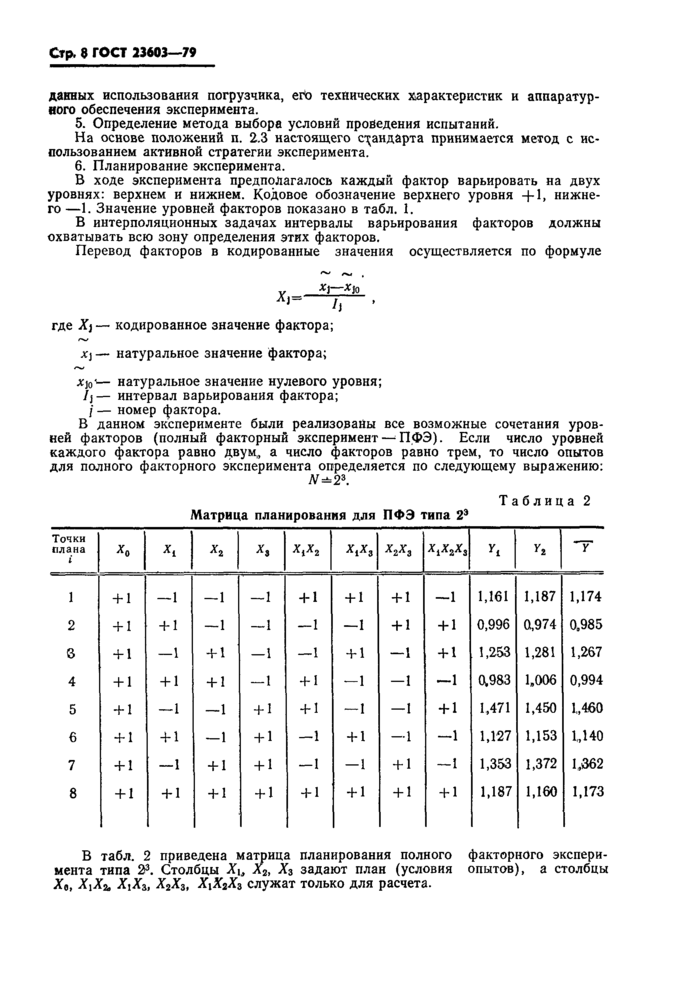
Таблица 2 Матрица планирования для ПФЭ типа 2Э | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
В табл. 2 приведена матрица планирования полного факторного эксперимента типа 23. Столбцы Xt, л2, Х3 задают план (условия опытов), а столбцы Х9, Х^Хъ ХхХ3, Х2Х3, ХхХ2Хг служат только для расчета.
ГОСТ 23603-79 Стр. 9
В планировании эксперимента используются кодированные значения фактора + 1 и —1. В матрице планирования строки соответствуют различным опытам, а столбцы—значениям фактора. Каждый столбец в матрице планирования называется вектор-столбцом, а каждая строка — вектор-строкой.
Составленная матрица планирования обладает следующими свойствами: симметричность относительно центра эксперимента, заключающаяся в том, что сумма элементов вектор-столбца каждого фактора равна нулю или
N
2*1.=о,
i-1
где / — номер фактора, N — число опытов в матрице;
свойство нормирования — сумма квадратов элементов каждого столбца равна числу опытов или
2 хъ -*•
1-1
ортогональность — сумма почленных произведений любых двух вект.ор-столбцов матрицы равна нулю или N
\Фи> /’ и~0, 1,2.....k.
1-1
7. ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА
Эксперимент проводился на специальной испытательной площадке. Для имитации операции штабелевки использовалась специальная эстакада с фиксированными площадками для подъема груза (высотой 1,4 и 2,8 м) и два стандартных контейнера разного веса (0,5 и 2,0 т). Трасса пробега проходила но окружности соответствующей длины.
Последовательность рабочего цикла: съем груза с эстакады; перемещение груза но окружности; подъем груза на эстакаду; холостой пробег по окружности.
Каждый опыт матрицы планирования проводился два раза (два повторных опыта). Фиксировалось время работы погрузчика в каждом опыте. Для фиксации потребления энергии и тока использовались соответствующие электрические счетчики.
За функцию отклика было принято потребление электроэнергии за 1 с в ватт-часах. Для этого показания счетчика делились на время опыта.
Для исключения систематической ошибки (дрейфа) проводилась рандомизация опытов при помощи таблицы случайных чисел. Опыты матрицы планирования выполнялись в следующей последовательности: 1, 3, 4, 7# 2, 5, 6, 8. При проведении эксперимента погрузчиком управлял высококвалифицированный водитель.
8. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПОЛИНОМИАЛЬНОЙ МОДЕЛИ НА ОСНОВЕ МЕТОДОВ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
8.1. Проверка однородности дисперсии и подсчет дисперсии воспроизводимости.
Эксперимент, содержащий конкретное число опытов, позволяет получить только выборочные оценки для коэффициентов уравнения, их точность и надеж-