ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

КОЛИЧЕСТВЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ ПАРАМЕТРОВ ОБЪЕКТОВ СТАНДАРТИЗАЦИИ

МЕТОДЫ ОБЕСПЕЧЕНИЯ КОМПЛЕКСНОСТИ

основные положения ГОСТ 18.401-77

Издание официальное

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СТАНДАРТОВ СОВЕТА МИНИСТРОВ СССР

Москва

РАЗРАБОТАН И ВНЕСЕН Всесоюзным научно-исследовательским институтом стандартизации (ВНИИС)

Директор А. В. Гличев Руководитель темы В. В. Ткаченко Зам. руководителя темы Д. М. Комаров

Исполнители: Н. Д. Алексеева, Ю. С. Вениаминов, Е. В. Извеков, С. А. Клавина, Г. В. Питмане, А . В. Матвеев, О. Ф. Пославский, Е. Н. Пронина, М. Л. Сыроватко, Г. С. Табакова

ПОДГОТОВЛЕН К УТВЕРЖДЕНИЮ Всесоюзным научно-исследовательским институтом стандартизации (ВНИИС)

Директор А. В. Гличев

УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета стандартов Совета Министров СССР от 12 декабря 1977 г» № 2858

ГОСТ 1В.401—77 Стр. 9

2.10.    С целью упрощения вычислений по моделям, содержащим много взаимосвязанных оптимизируемых параметров, случайные числа и случайные функции, нелинейность относительно оптимизируемых параметров и учитывающим изменения во времени, а также для облегчения проверки и коррекции моделей следует широко использовать в качестве вычислительной процедуры имитационные эксперименты на ЭВМ по построенным математическим моделям.

2.11.    По возможности следует исходную сложную модель разделить на более простые модели, которые могут быть решены какими-либо численными методами.

3. СОСТАВ И ОБОЗНАЧЕНИЯ МЕТОДИЧЕСКИХ И НОРМАТИВНО-ТЕХНИЧЕСКИХ ДОКУМЕНТОВ ГРУППЫ

3.1. Межотраслевые методические и нормативно-технические документы, регламентирующие методы обеспечения комплексности, оптимизации, классифицируются на подгруппы в соответствии с табл. 2.

Таблица 2 Подгруппы документов, устанавливающие методы обеспечения комплексности

Код подгруппы Наименование подгруппы документов 40 Основные положения 41 Методы оценки применимости и коррекции границ комплексности 42 Методы оптимизации параллельных комплексов 43 Методы оптимизации последовательных комплексов 44 Методы оптимизации комбинированных комплексов 45 Составление и анализ связанных математических моделей 46 Резерв 47 Резерв

3.2. Допускается классифицировать отраслевые документы, определяющие методы обеспечения комплексности, по особенностям объектов стандартизации.

ПРИЛОЖЕНИЕ / Справочное

КОМПЛЕКСНОСТЬ ОПТИМИЗАЦИИ И МЕТОДЫ ЕЕ ОБЕСПЕЧЕНИЯ

Комплексность стандартизации характеризуется комплексностью оптимизации, а также степенью охвата стандартизацией совокупности взаимодействующих объектов и параметров и совокупностью взаимосвязанных стандартов.

Как правило, не вся совокупность стандартизуемых элементов объекта комплексной стандартизации оптимизируется совместно. Элементы объекта комплексной стандартизации могут разбиваться на группы, каждая из которых оптимизируется отдельно, при этом допускается' включение одного и того же элемента в две и более группы).

Кроме того, некоторые оптимизируемые параметры могут быть не записаны в стандартах (например, обобщенные показатели качества) и, наоборот, не все стандартизируемые параметры оптимизируются; часть этих параметров может быть задана в виде ограничений.

Комплексность оптимизации необходима для обеспечения эффективности комплексной стандартизации -

Без достаточного уровня комплексности оптимизации нельзя в полной мере обеспечить оптимальное удовлетворение требований заинтересованных организаций и предприятий путем согласования параметров взаимосвязанных компонентов, входящих в объекты комплексной стандартизации, 9 увязку сроков введения в действие стандартов.

Методы обеспечения комплексности при теоретической оптимизации — это-совокупность приемов (операций), а также порядок составления соответствующих математических моделей оптимизации при широких границах комплексности. Эти методы содержат также рекомендации по выбору математической процедуры определения оптимальных параметров по уже составленной модели.

В случае эксперимент а льной оптимизации методы обеспечения комплексности — это совокупность приемов (операций) разработки (выбора, модернизации) соответствующих технических устройств, планирования экспериментов и обработки данных экспериментов при широких границах комплексности.

Ввиду того, та) с расширением границ комплексности существенно возрастают трудности составления, проверки применимости и коррекции математической модели, настоящий стандарт предназначен главным образом для обеспечения координации разработки и повышения унификации этих моделей с целью обеспечения широкого применения их в народном хозяйстве.

ГОСТ 18.401-77 Стр. 11

ПРИЛОЖЕНИЕ 2 Справочное

ОСНОВНЫЕ ОБЪЕКТЫ СТАНДАРТИЗАЦИИ,

КОТОРЫЕ ЦЕЛЕСООБРАЗНО РАССМАТРИВАТЬ КАК ПОСЛЕДОВАТЕЛЬНЫЕ

КОМПЛЕКСЫ

		Основные особенности оптимизации
Объект оптимизации	Оптимизируемые параметры	Р ассматривае-мые явления (процессы)	Основы построения структуры комплекса	Сущность учитываемых связей между элементами	Обеспечиваемое свойство стандартизации
1. Комп-	Парамет-	Функцию-	Причин	Преобра	Комплек
леке элемен-	ры продух-	ниров>аняе	но-следст	зование ма	сность,
гав продуй-	шш	(примене-	венная оче	териала,	иногда опе-
дни		ние, использование) продукция и затраты на ее разработку я производство	редность	энергии (силы)), информации	режаемость
2. Техно	Парамет	Производ	Всегда	Преобра	То же
логический	ры операций	ство про	очередность	зование из
процесс	(групп операций, переходов)	дукции, оказание услут	операций во времени, иногда и причинно-следственная очередность	делии, полуфабриката, энергии, информации
3. Сово	Измене	Совершен	Очеред	То же,	Комплек
купность	ние пара*-	ствование	ность во	что и в под	сность и
двух и более	метров про	продукция	времени и	пункте 1 и	опережае-
последовательных во временя моделей продукция ■	дукции во временя		причинно-следственная очередность	использование задела оборудования, материалов, элементов, знаний, опыта	мость

Продолжение

Основные особенности оптимизации Объект оптимизации Оптимизируе мые параметры Рассматриваемые явления (процессы) Основы построения структуры комплекса Сущность учитываемых связей между элементами Обеспечиваемое свойство стандартизации 4. Сово- Измене- Оов ер- Причинно- То же, Комплек куш ОСТЬ ние пара- шенствова- следствен что в под сность и двух и бо- метров двух ние про- ная очеред пунктах 1 опережае- лее последовательных во времени последовательных комплексов и более заменяющих друг друга во времени последовательных комплексов продукции дукции ность и очередность во времени замены моделей продукции и 3 мость Изменение параметров операций двух и более заменяющих друг друга во времени технологи-чески х процессов, являющихся последовательными 'комплексами Совершенствование технологических процессов Очередность операций и технологических процессов во времени То же, что в подпунктах 2 и 3 То же

ГОСТ 18.401-77 Стр. 1*

ПРИЛОЖЕНИЕ 3 Справочное

БАЗОВЫЕ МЕЖОТРАСЛЕВЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОПТИМИЗАЦИИ ПРОСТЕЙШИХ ПОСЛЕДОВАТЕЛЬНЫХ КОМПЛЕКСОВ

1. Пространственная базовая математическ-ая модель оптимизации простей^ шах последовательных комплексов

1.1. Ка^ждый л-ый элемент простейшего последовательного комплекса содержит набор оптимизируемых параметров

P(n)=(P_t(n), Р_г(п).....Рк_п{п)\    (О

где k_n — число сяхтимизаргувмых параметров я-no элемента^

Вектор Р(п) принадлежит некоторому множеству { Р(п) } его допустимых значений

Р(п)£{Р(п)1    (2)

Вход в первый элемент комплекса х(1) или #(0) совпадает с входом комплекса

х(1)-У(0)«х_х.    (3)

Входом в каждый последующий элемент п служит выход предыдущего* (п—1) элемента

7(п) =^(n-l)=(j/i(n—1), Уг(п—1),.у^ ^п—I)),    (4)

где п=2.....N;

N — число элементов комплекса;    __

u_n_i — число составляющих вектора выхода у(п—1).

Вектор ~у( л—1) принадлежит некоторому множеству {,у(п—1)} его допустимых значений

7(л-1)€(Р(«-1)}.    (5)

Выход я-го элемента равен

U(n)=((yi{n), У2(п),---.Уи_п(п)).    (⁶)

где

~у(п)Шп)},    (7)

(7(п)} — множество допустимых значений вектора у(п).

Вььхюд последнего элемента совпадает с выходом .всего комплекса

f(N)=~y_K.

Выход я-то элемента является функцией оптимизируемых параметров и вхо

да

y(n)=F^lnl(«/(n-l), Р(п))

или

y_l(n)= F^l^^]{ydn—1), Уг(п—1).....Уи_п_,(/1—1); Р_х{п), Р_г{п).....P_ka(я));

у₈(л)=»И^л1 (уЛп-1), у_г(п-1).....y_tt„-ii.n-l); Р^п^Р^п), .... Pk_n(n))\

Va_n{n)=F^^]{yi{n-\), y_t(n-1).....Vu_n-i(n-l); Р_г(п), P_t(n).....P*„(«)),

где

ft"!=(/?}«!, F^, ...,    —    вектор-функция преобразования элемента n.

Граничными условиям могут быть

I Jr^=i/(0)    —    фиксирован,

1Ук=у(Ю — не фиксирован, [^=^(0)    —    не фиксирован,

Ук=У(Ю — фиксирован, =£(0)    —    фиксирован,

У    —    фиксирован.

Зависимости (1)—(9) составляют пространственную базовую математическую модель функционирования простейшего последовате льного комплекса.

1.2. Для построения пространственной базовой математической модели оптимизации к зависимостям (1)—(9) необходимо добавить выражение целевой функции и, иногда, дополнительные ограничения.

Целевая функция оптимизации часто имеет вид

Д= Ф (J(N)) +    (F(n-1), Р(П)),    (10)

где 0(#(W)) функции выхода комплекса;

^п^(у(п—1), Р(п)) — функция, которая оценивает вклад каждого отдельного элемента в достижение цели.

Функция Gl«l обычно -выражает затраты 3[л1на создание и функционирование л-го элемента, эффект 31л] или прибыль 31л]—31л[ от л-по элемента.

Оптимизация заключается в нахождении значений оптимизируемых параметров, при которых целевая функция достигает максимального (минимального]! значения.

2. Пространственно-временная базовая математическая модель оптимизации простейших последовательных комплексов

2.1. Каждый л-ый элемент простейшего последовательного комплекса содержит Кп олтимизир уемых параметров, значения которых зависят от времени

Р(п, t) = (р₈(я, о. Ра (Л, О.....Pk_n{n, 0).    (И)

.Вектор Р(л, t) принадлежит некоторому множеству { Р(л, /)} его допустимых значений

Pin,    t)}.    (12)

Некоторые неоптимизируемые конструктивные параметры элемента также могут быть функциями времени вследствие износа, выгорания, перемещения касс и др., т. е.

ГОСТ 18.401-77 Стр. 15

Pc(n>t)*~ (P_Ci{n,t), P_Cf(n,t).....Pc_m (n, t)),

где

m_n — число переменных во времени нештммязюруемых параметров гс-го элемента!.

Вход в первый элемент комплекса совпадает с входом всего комплекса

*0. 0 =**«)-■£(0, 0.    (14)

Входом в каждый последующий элемент служит выход предыдущего (п—1)-го элемента

х(п, 0 ⁼ У(п 1, t)=>(yi(n~\, t), .... y_Un-i(n— 1, О).    (15)

где

3, . . . , N\

N — число элементов комплекса;    ___

«_я_1 — число составляющих вектора входа у(п—1, /).

Вектор у(п—1, t) принадлежит некоторому множеству {у(п—1, 0} его допустимых значений:

У(п~ 1. 06 (МП—!,<)}•    О⁶)

Выход д-го элемента равен

7(П. t)={yi(n, t), у_г{п, t).....Уи_п{п, /)),

где

У(л, 0 £ (Щп-1, ()}.    (17)

Выход последнего элемента совпадает с выходом комплекса

y(N, t)=y_K{t).

Выход n-mo элемента является функцией входа, оптимизируемых параметров и времени:

y(n, 0=F^tn,(y(n-l. t),P(n,    (18)

Влияние изменений неопгим'изируемых конструктивных параметров учитывается как функция от t.

Часто вместо уравнение (18) составляется дифференциальное уравнение

—37^-    t),~P(n,    i),    t).    (18')

При наличии дифференциальных уравнений (18') в математическую модель функцпошрования необходимо включить начальные условия (состояние в момент t=to).

£/(п, 0=tf*(n. *о)-

Стр. 16 ГОСТ 18.401-77

Граничными условиями могут быть

—    заданная функция времени;

—    незаданная функция времени;

—    незаданная функция времени;

—    заданная функция времени;

—    заданная функция времени;

—    заданная функция времени;

—    незаданная функция времени;

—    незаданная функция времени.

Зависимости (11)—(19) составляют пространственно-временную базовую ■математическую модель функционирования простейшего последовательного комплекса.

2.2. Для построения пространственно-временной базовой математической модели оптимизации простейших последовательных комплексов к зависимостям <1 l)i—(19) необходимо добавить выражение целевой функции и иногда дополнительные ограничения, например, по производственным возможностям.

Целевая функция оптимизации часто имеет вид

Ц    0.    Р(я.    О,    о]<«    +    Ф(г/(ЛГ.    <!)).    (20)

/t — заданный (конечный момент времени или момент времени, для которого задан y(N_f /).    _

Второе слагаемое $(y(N_t ti)) выражает влияние состояния N-го элемента в •момент t_x.    __

Подынтегральная функция GM зависит от изменения состояния у(п—1, t)_t

значений параметров Р(л, /), времени t и включает приведение эффектов и затрат к одному моменту времени.

2.3.    Пространственно-временная модель, рассмотренная в пп. 2.1; 2.2, учитывает изменение во времени входа комплекса, конструктивных параметров элементов (вследствие износа, повреждения, изменения массы объекта в результате выгорания топлива и других химических реакций, р>асхода материалов, перемещения массы, биологических процессов и др.), начальных возмущений, а также экономических и социальных условий.

2.4.    С целью расширения области применения базовых моделей оптимизации дростейших последовательных комплексов входами и выходами в этих моделях считают лишь параметры состояния рассматриваемого процесса (состояние полуфабриката, модели продукции, энергии, деятельности), не включающие затраты и эффекты, связанные с созданием и эксплуатацией данного элемента и учитываемые функциями GM.

2.5.    Применять указанные базовые модели для разработки рабочих моделей следует в соответствии с таблицей.

ГОСТ 18.401-77 Стр. 17

Рабочая модель Базовая модель по динамичности по числу ступеней1 значений оптимизируемых параметров по уровню неопределенности Пространствен- Статическая Одноступенча Детерминированная ная То же тая То же Вероятностная Квазистатиче Детерминированная Временная3 ская2 То же » Вероятностная Динамическая Многоступен Детерминированная без разделения комплекса на элементы ГГо же чатая То же Вероятностная Пространствен Динамическая с Одноступенча Детерминированная но-временная разделением комп тая лекса на элементы То же ГГо же Вероятностная » Многоступен Детерминированная > чатая То же Вероятностная

¹    Число ступеней значений оптимизируемых параметров — число одновременно оптимизируемых, сменяющих друг друга, моделей продукции.

²    Квазистатическая модель — по ГОСТ 18.001-76.

³    В данном случае последовательный комплекс получается при рассмотрении состояний объекта в некоторые моменты времени как отдельных элементов. Число элементов равно числу рассматриваемых моментов времени (числу состояний). Для таких задач можно пользоваться пространственной базовой моделью, заменяя в ней номер элемента на номер момента времени.

3. Использование базовых математических моделей оптимизации простейших последовательных комплексов.

3.1. Примеры использования пространственной базовой математической модели оптимизации простейших последовательных комплексов¹.

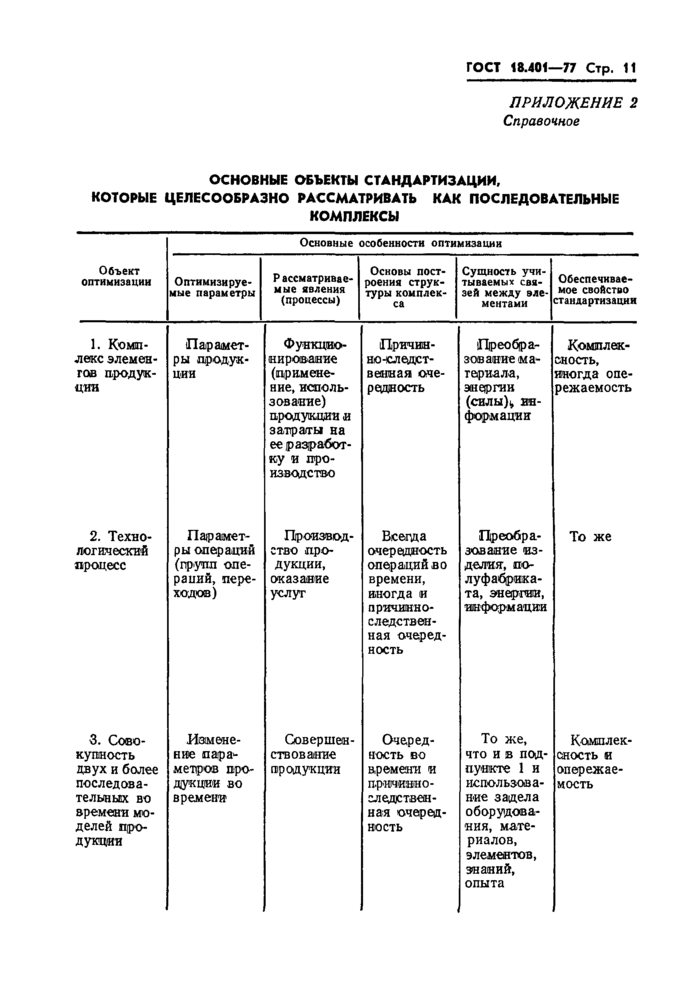
Пример 1. Оптимизация системы трубопроводов [11].

Необходимо транспортировать поток нефти Q с помощью N последовательно расположенных насосных станций, при этом начальное давление всасывания (Ps) и расстояние от начала трубопровода по л-ой станции L _п и давление в конечном пункте y(N)—y^—(P_s)^ .

ут

На промежуточных насосных станциях потоку Q сообщается энергия, достаточная для томпенсации потерь давления за счет трения жидкости в трубопроводе и подъема жидкости на соответствующую высоту. Диаметр трубопровода постоянный.

Элементом рассматриваемого простейшего последовательного комплекса можно считать каждую насосную станцию с отходящим от нее участком трубопровода (до следующей насосной станции).

На каждой насосной станции необходимо сообщить потоку такое дополнительное давление Р(п)_% при котором обеспечивается требуемое давление {Ps)r в конечном пункте и минимальные приведенные суммарные затраты на транспортирование нефти.

В зависимости от конкретных условий могут быть поставлены другие задачи, например, оптимизация параметров насосов для каждой станции.

Эскизная схема структуры и функционирования представлена на черт. 1.

Математическая; модель функционирования

Входом первого элемента является *к=у(0) = (Ду)ь Входом п-го элемента, п=2, 3, . . . , N является результирующее давление, создаваемое всеми первыми (п—1) насосными станциями с учетом потерь на участке трубопровода от первой до л-ой станции

y(n-]) = (P_s)_a.

УДК 006.1:006.354    Группа    45f

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

Количественные методы оптимизации параметров объектов стандартизации

МЕТОДЫ ОБЕСПЕЧЕНИЯ КОМПЛЕКСНОСТИ

Основные положения

Quantitative methods of optimization for parameters of standardization objects. Methods for providing integrity. Basic aspects

Постановлением Государственного комитета стандартов Совета Министров СССР от 12 декабря 1977 г. № 2858 срок действия установлен

с 01.01. 1979 г. до 01.01. 1984 г»

Настоящий стандарт устанавливает основные положения, содержащие требования к методам обеспечения комплексности оптимизации параметров объектов стандартизации, классификацию* группы методических и нормативно-технических документов, регламентирующих методы обеспечения комплексности, а также термины и определения основных понятий, используемых при обеспечении комплексности оптимизации.

1. ОСНОВНЫЕ ПОНЯТИЯ

1.1.    Комплексность оптимизации параметров объектов стандартизации (комплексность ОПОС) — свойство оптимизации, характеризуемое принятыми границами комплексности и определяющее точность и подробность оптимизации (см. справочное приложение 1).

1.2.    Границы комплексности — границы, определяющие совокупность совместно оптимизируемых параметров объекта стандартизации и факторов, учитываемых при оптимизации и влияющих на оптимальные значения параметров.

1.3.    Методы обеспечения комплексности оптимизации параметров объектов стандартизации — методы, позволяющие производить оптимизацию при достаточно широких границах комплексности.

Перепечатка воспрещена

© Издательство стандартов, 1978-

ГОСТ 18.401-77 Стр. 19

Выходом п-ю элемента является результирующее давление всасывания (Ps)_n+1 следующей станции, создаваемое всеми предыдущими насосными станциями с учетам потерь на участке от первой до (я+1) станции

y(n)=(Ps)_n+(22) Выходом N-iro элемента (выходом комплекса) является давление

(Рз)_К=У(Н)=У_к.    (23)

Оптимизируемым параметром Р (я) л-го элемента является повышение давления, создаваемое л-ой насосной станцией.

Уравнение преобразования элемента имеет вид

^(n)=i/(n-l)+P(n)-AP(«)(L_n+1-L_w)-fe(£_rt+1-£_ft),    (24)

где

у(п— 1) — (Р$)_п — давление всасывания я-й станции;

А Р(п) — потеря давления за счет трения на единице длины ва участке я-го элемента;

Е_п+\ *—Еп — разность высот (я-И)-й и я-й насосных станций; k — коэффициент пропорциональности;

—L_n — длина трубопровода на участке я-го элемента.

Математическая модель оптимизации

Математическая модель оптимизации составлена для случая, когда известны данные для расчета потерь на трение в трубопроводах и размещение насосных станций и следует оптимизировать только величину повышения давления Р(п), исходя из целевой функции минимума приведенных суммарных затрат. Это сводится к оптимальному выбору числа и типов насосов на каждой станции.

Математическая модель оптимизации в этом случае будет состоять:

из уравнений преобразований элементов

)«9(0)+Р( 1) - АР( 1) (U-LJ ~~k (Et-~E_t), y(2)=y(l)+P(2)-AP(2)(L_i-L_t)-ft(£_i-^_t),    (25)

V(N)=V(N-l)+P(N)-bP(NHL_N+l-L_N)-HE_N+l -E„);

'Граничных условий на левом и правом концах

1. Ук=(^р*)к'*    <²⁶>

целевой функции приведенных суммарных затрат на транспортировку нефти. Пример 2. Оптимизация параметров отдельных участков трубопровода

[14].

Участок трубопровода можно рассматривать как простейший последовательный комплекс, состоящий из трех элементов: электродвигателя, который дает механическую мощность W в течение времени действия системы Г, насоса, обеспечивающего перекачку, например, нефти с расходом ее Q на расстояние L.

С увеличением диаметра трубопровода D уменьшается гидравлическое сопротивление движению нефти и, следовательно, уменьшается необходимая мощность двигателя и расход электроэнергии. Однако с увеличением диаметра трубопровода возрастают затраты на изготовление и установку трубопровода и на его ремонт. Следовательно, существует некоторый оптимальный диаметр трубопровода.

1.4.    Оптимизируемый комплекс в задачах оптимизации параметров объектов стандартизации — оптимизируемый объект стандартизации, представляющий совокупность двух и более элементов.

1.5.    Элемент комплекса — часть комплекса, у которой теоретически или экспериментально можно определить вход и выход и установить зависимость выхода от входа, определяемую природой элемента.

Вход и выход элемента представляют собой скалярные или векторные величины, имеющие определенный физический, экономический и социальный смысл. Входами и выходами могут быть величины, значения которых характеризуют изделия, продукты, процессы.

К элементам комплекса относятся машины, сборочные единицы, детали, технологические операции, объекты в разных состояниях и в отдельные моменты времени и т. д.

Расчленение комплекса на элементы определяется требуемой точностью, подробностью и целью оптимизации и наличием данных о связях между параметрами объекта.

1.6.    Одномерный элемент комплекса — элемент комплекса, вход и выход которого представляют собой скалярные величины (черт. 1).

1.7.    Многомерный элемент комплекса — элемент комплекса, вход и (или) выход которого представляют собой векторные величины (черт. 2).

Черт. 2

1.8. Завершенный элемент комплекса — элемент комплекса, обладающий следующими свойствами:

элемент может функционировать независимо от функционирования остальной части комплекса;

в случае прекращения функционирования элемента остальная часть комплекса может функционировать, однако эффективность комплекса при этом снижается.

ГОСТ 18.401-77 Стр. 3

Номенклатура составляющих вектора выхода завершенного элемента входит в номенклатуру составляющих вектора выхода комплекса.

1.9.    Незавершенный элемент комплекса — элемент комплекса, не обладающий хотя бы одним из свойств завершенного элемента.

1.10.    Односторонняя связь между элементами комплекса — связь, при которой выход одного элемента (например, i-ro) полностью или частично является входом или часть входа другого элемента (например, /-го) и никакая часть выхода /-го элемента не является хотя бы частью входа i-го элемента (черт. 3).

t-й элемент называется предыдущим, /-й элемент — последующим.

1.11.    Двусторонняя связь между элементами комплекса — связь, при которой не только выход или часть выхода одного элемента (например, i-ro)^; является входом или частью входа другого элемента (например, /-го), но и выход или часть выхода /-го элемента является входом или частью входа t-го элемента (черт. 4) i

Односторонняя связь

_п J

L -j -

Г

Черт. 3

1.12.    Последовательное соединение элементов комплекса — соединение элементов комплекса с помощью односторонних связей.

1.13.    Последовательный комплекс — комплекс, состоящий из незавершенных элементов, в котором любая пара связанных элементов соединена последовательно.

Основные объекты стандартизации, которые при оптимизации их параметров целесообразно рассматривать как последовательные комплексы, приведены в справочном приложении 2.

1.14.    Простейший последовательный комплекс — последовательный комплекс, в котором выход любого элемента (кроме последнего) совпадает с входом последующего.

Вход простейшего последовательного комплекса совпадает с входом первого элемента, а выход — с выходом последнего элемента.

1.15.    Полная заменяемость элемента комплекса — возможность замены элемента комплекса с одними параметрами на эле-

Стр. 4 ГОСТ 18.481-77

мент (элементы) с другими параметрами без изменения эффективности функционирования комплекса.

Ограниченная заменяемость элемента комплекса — возможность замены элемента комплекса с одними параметрами на элемент (элементы) с другими параметрами, приводящая к снижению эффективности функционирования комплекса.

1.16.    Параллельный комплекс — комплекс, состоящий из завершенных элементов с ограниченной заменяемостью.

Параметрический ряд в задачах оптимизации является частным случаем параллельного комплекса, у которого векторы выхода каждого элемента и всего комплекса имеют одинаковую номенклатуру составляющих.

1.17.    Эффективная совокупность значений параметров комплекса многоцелевого назначения — совокупность значений параметров, в которой любое изменение значения параметра (или нескольких параметров), приводящее к повышению уровня достижения хотя бы одной цели при данных условиях, обязательно приводит к снижению уровня достижения хотя бы одной другой цели.

Совокупность оптимальных значений параметров комплекса является частным случаем эффективной совокупности значений параметров.

1.18.    Базовая математическая модель оптимизации — модель оптимизации большого класса комплексов: данной отрасли или нескольких отраслей, предназначенная для составления рабочих математических моделей оптимизации конкретных объектов (комплексов) .

В базовой математической модели не обязательно раскрывать все математические выражения до степени детализации, достаточной для разработки программы вычисления на ЭВМ.

Базовые межотраслевые математические модели оптимизации простейших последовательных и параллельных комплексов приведены соответственно в справочных приложениях 3 и 4.

1.19.    Рабочая математическая модель оптимизации — модель оптимизации, содержащая всю информацию, необходимую для оптимизации комплекса.

1.20.    Унифицированный ряд математических моделей оптимизации — совокупность рабочих математических моделей оптимизации, обеспечивающих решение некоторого класса задач отрасли ^предприятия).

Модели унифицированного ряда отличаются друг от друга границами комплексности, степенью неопределенностей, способом учета неопределенностей, полнотой учета изменения во времени и другими особенностями, которые отражаются на видах математических зависимостей и вычислительных процедурах.

ГОСТ 18.401-77 Стр. 5

2. ОСНОВНЫЕ ТРЕБОВАНИЯ К МЕТОДАМ ОПТИМИЗАЦИИ ПАРАМЕТРОВ ОБЪЕКТОВ СТАНДАРТИЗАЦИИ ДЛЯ ОБЕСПЕЧЕНИЯ КОМПЛЕКСНОСТИ

ОПТИМИЗАЦИИ

2.1.    Основные требования к методам оптимизации параметров объектов стандартизации — по ГОСТ 18.001-76, разд. 2.

2.2.    По мере расширения границ комплексности с целью удовлетворения требований к методам оптимизации по точности, подробности и своевременности, а также обеспечения широкого применения этих методов в народном хозяйстве следует:

использовать разные постановки задач оптимизации комплекса; координировать работы разных специалистов и организаций, составляющих математические модели оптимизации;

увеличить уровень унификации и агрегатирования математических моделей и вычислительных процедур;

более полно осуществить проверку применимости и коррекции используемых математических моделей;

шире использовать сочетания теоретических методов оптимизации с экспериментальными методами оптимизации и с приближенными методами обоснования;

учитывать многоцелевое назначение объектов стандартизации; сочетать имитационные эксперименты на ЭВМ по математическим моделям с методами математического программирования и другими вычислительными процедурами;

увязать задачи автоматизированной системы оптимизации параметров объектов стандартизации с другими задачами смежных АСУ.

2.3.    В зависимости от функции управления качеством, для выполнения которой производится оптимизация, наличия исходных данных, времени, разработанных методов и средств оптимизации, используемые для оптимизации данного комплекса математические модели должны отличаться друг от друга совокупностью оптимизируемых параметров и элементов комплекса, анализируемыми явлениями (процессами), степенью агрегатирования параметров и другими особенностями.

Некоторые параметры и элементы комплекса входят в две и больше модели, а некоторые математические модели охватывают весь комплекс и его взаимодействие с другими объектами.

2.4.    С целью координации работ различных специалистов и обеспечения их специализации процесс построения математических моделей оптимизации параметров комплекса, выполняемый по ГОСТ 18.101-76, следует проводить в три этапа:

построение эскизной схемы структуры и функционирования комплекса;

построение математической модели функционирования комплекса;

Стр. 6 ГОСТ 18.401-77

построение математической модели оптимизации комплекса-(составление целевой функции и дополнительных ограничений). Схема распределения работ по этапам приведена в табл. 1.

Таблица I

Типовая схема распределения работ по построению математической модели комплексной оптимизации

Выполнение этапов работы Содержание работ построение эскизной схемы структуры и функционирования построение математической модели функ- ] ционироваиия построение математической модели оптимизации 1, Словесная постановка задачи оптимизации, в ггом числе построение дерева целей Иногда выполняется предварительно Выполняется предварительно Уточняется 2. Словесное описание функционирования комплекса Выполняется Уточняется То же 3. Выделение комплекса из среды Выполняется предварительно То же г* 4.    Расчленение комплекса на элементы 5.    Установление номенклатур ы пар аметров комплекса: То же » i> оптимизируемые технические параметры » » остальные технические параметры > » ■» экономические показатели (затраты, эффекты) Не выполняется или выполняется предварительно Может уточняться *» 6.    Составление функции преобразования для элементов 7.    Составление ограничений на: 'Выполняется предв арител ьно без детализация Уточняется оптимизируемые технические параметры Иногда выполняется Выполняется остальные технические параметры То же То же затраты и эффекты Не выполняется Не выполняется (Выполняется 8. Составление граничных условий Иногда выполняется предварительно Выполняется, иногда предварительно То же 9. Прогнозирование изменений исходных данных Не выполняется Не выполняется

Продолжение табл. 1

Выполнение этапов работы Содержание работ построение эскизной схемы структуры и функционирования построение математической модели функционирования построение математической модели оптимизации 10. Предварительное прогнозирование части параметров, подлежащих оптимизации Не выполняется ‘Не выполняется Выполняется 11. Формализация целевой функции То же То же То же 12. Уточнение формулировки задачи оптимизации » 13. Придание модели вида, удобного для вычисления * Иногда выполняется » 14 Проверка точности Выполняется Выполняется и сложности модели оптимизации (границ комплексности) предварительно предварительно 16. Коррекция математической модели оптимизации » Не выполняется То же

Примечание. Подпункты 14 и 15 выполняются также при разработке алгоритма вычисления и после пробных вычислений.

2.5. Для обеспечения комплексности оптимизации составляют следующие математические модели: базовые межотраслевые; базовые отраслевые;

унифицированные ряды математических моделей отрасли (предприятия).

2.5.1.    Построение унифицированного ряда математических моделей обеспечивает более высокий уровень унификации, чем построение базовых математических моделей. Базовые отраслевые модели следует применять при отсутствии информации для построения унифицированного ряда моделей.

2.5.2.    Для увеличения числа задач, решаемых по данной математической модели, и уменьшения числа необходимых моделей следует увеличить их универсальность. Но это усложняет модели и затрудняет их применение в конкретных случаях.

Целесообразную универсальность и целесообразное число моделей унифицированного ряда следует определять на основе анализа следующих факторов:

количество задач, решаемых при помощи данной модели;

средний эффект использования унифицированной модели при решении одной задачи в результате упрощения составления модели и вычислений.

2.6.    При определении целесообразных границ комплексности по мере их расширения следует в процессе построения модели и при вычислении оптимальных параметров более строго производить количественную проверку применимости используемой математической модели и при необходимости ее корректировать согласно общей схеме оптимизации параметров объектов стандартизации по ГОСТ 18.101-76.

2.6.1.    Применимость данной математической модели следует проверять оценкой влияния принимаемых допущений на результаты оптимизации и (или) сравнением результатов расчета и опыта.

Целесообразно отдельно проверять точность и подробность математической модели функционирования, для которой обычно легче получить опытные данные, чем для всей модели оптимизации.

2.6.2.    Для проверки применимости данной математической модели следует предусмотреть соответствующие расчеты, имея специальный блок (блоки) в математической модели оптимизации, или по специальной математической модели.

2.7.    Агрегатирование математических моделей заключается в сочетании готовых блоков общей схемы оптимизации параметров объектов стандартизации, а также в агрегатировании блоков из отдельных элементов.

2.8.    По мере увеличения комплексности следует шире использовать сочетания строгих методов оптимизации с приближенными и теоретических методов с экспериментальными (ГОСТ 18.001-76).

При использовании строгих теоретических методов согласно общей схеме оптимизации параметров объектов стандартизации (ГОСТ 18.101-76) следует раскрыть функционирование объекта, эффекты, затраты, составить ограничения и целевую функцию.

Область применения приближенных методов определяют согласно справочному приложению 5.

2.8.1. Макрометоды при их сочетании со строгими методами следует применять преимущественно для получения исходных зависимостей или агрегированных показателей, которые затем используют при оптимизации строгими методами (см. справочное приложение 5).

По мере перехода от перспективного планирования к разработке стандартов, проектированию и аттестации качества продукции роль макрометодов уменьшается, а строгих методов увеличивается.

2.9.    С целью обеспечения комплексности оптимизации для учета многоцелевого назначения объекта стандартизации в случаях, когда методы ГОСТ 18.001-76, разд. 1 недостаточны, определяется эффективная совокупность, а затем выбирается оптимальный вариант из этой совокупности.

1

Из приведенных ниже примеров видно, что для оптимизации сложного комплекса мойсно применять несколько моделей, в каждой из которых оптимизируется только часть комплекса или часть его параметров. Однако в таких случаях для определения оптимальных параметров комплекса следует применять также модели, служащие для увязки результатов оптимизации отдельных частей. Полученные в примерах оптимальные значения параметров могут быть использованы при проектировании трубопровода и его частей и как исходные данные по потребностям (спросу) при оптимизации параметрических рядов диаметров груб, параметров насосов и т. д.