ГОСТ 11.010-81
Прикладная статистика. Правила определения оценок параметров и доверительных границ для биномиального и отрицательного биномиального распределений
Купить ГОСТ 11.010-81 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Устанавливает правила определения оценок и доверительных границ для параметров биномиального и отрицательного биномиального распределений по совокупности статистических данных, полученных на производстве в процессе измерений, испытаний и анализов, если эти данные подчиняются биномиальному или отрицательному биномиальному распределениям.
Отменен без замены.
Оглавление
1. Общие положения
2. Оценка параметра биноминального распределения
3. Определение доверительных границ для параметра биномиального распределения
4. Оценка параметра отрицательного биномиального распределения
5. Определение доверительных границ для параметра отрицательного биномиального распределения
Приложение 1 (справочное) Примеры применения правил стандарта
Приложение 2 (справочное) Теоретические основы стандарта
Литература
| Дата введения | 01.01.1982 |
|---|---|
| Добавлен в базу | 01.01.2019 |
| Завершение срока действия | 01.03.1987 |
| Актуализация | 01.01.2021 |
Организации:
| 30.03.1981 | Утвержден | Государственный комитет СССР по стандартам | 1666 |
|---|---|---|---|
| Разработан | Государственный комитет СССР по стандартам | ||
| Разработан | Министерство высшего и среднего специального образования СССР | ||
| Издан | Издательство стандартов | 1981 г. |
Applied statistics. Point and interval estimators for parameters of binomial and negative binomial distribution
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5
стр. 6
стр. 7
стр. 8
стр. 9
стр. 10
стр. 11
стр. 12
стр. 13
стр. 14
стр. 15

стр. 16

стр. 17
стр. 18

стр. 19

стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРИКЛАДНАЯ СТАТИСТИКА
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК ПАРАМЕТРОВ И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ БИНОМИАЛЬНОГО И ОТРИЦАТЕЛЬНОГО БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЙ ГОСТ 11.010-81
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ Москва
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРИКЛАДНАЯ СТАТИСТИКА
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК ПАРАМЕТРОВ И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ БИНОМИАЛЬНОГО И ОТРИЦАТЕЛЬНОГО БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЙ
Издание официальное
МОСКВА — 1981
|
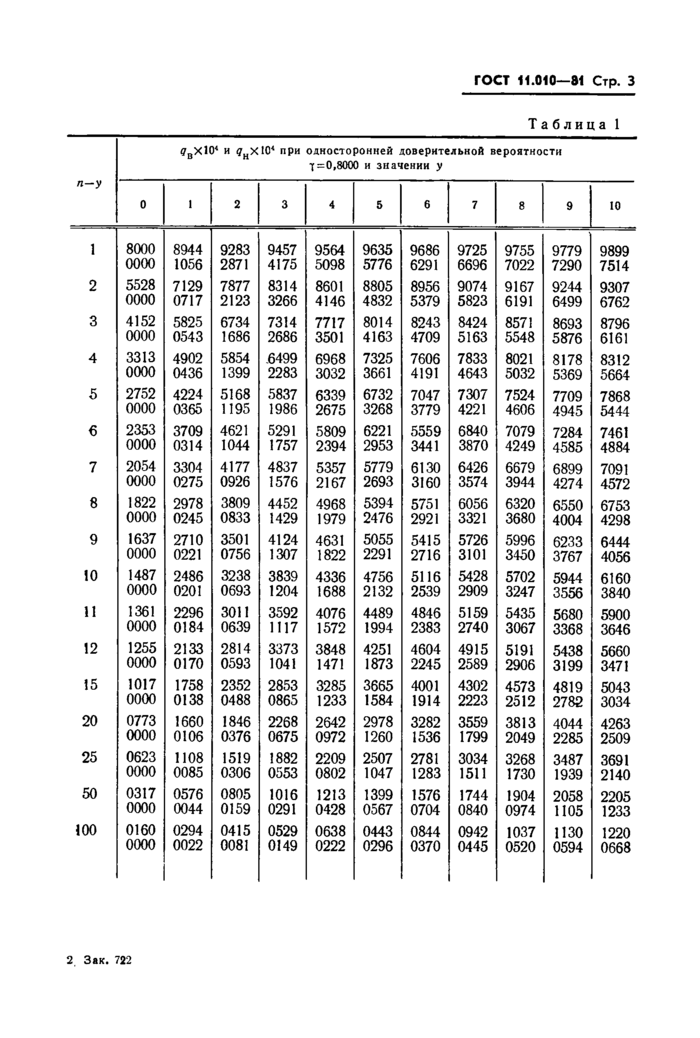
^gXlO4 и ?нхЮ4 при односторонней доверительной вероятности 7 = 0,9950 и значении у | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
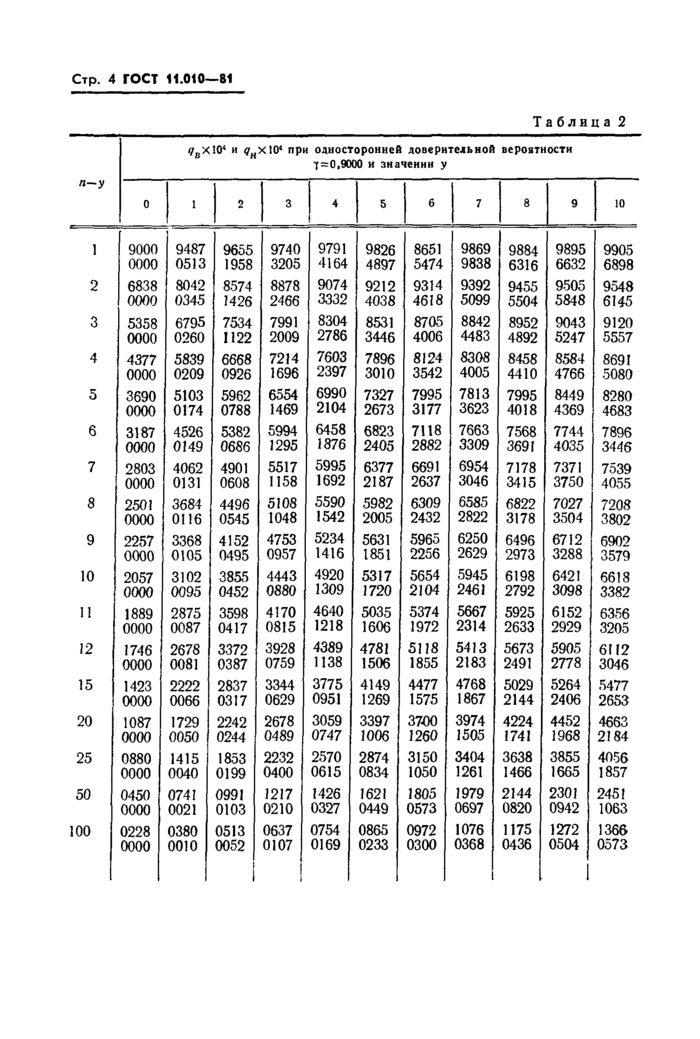
|
^gXlO4 и ?НХ104 при односторонней доверительной вероятности 7=0,9975 и значении у | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
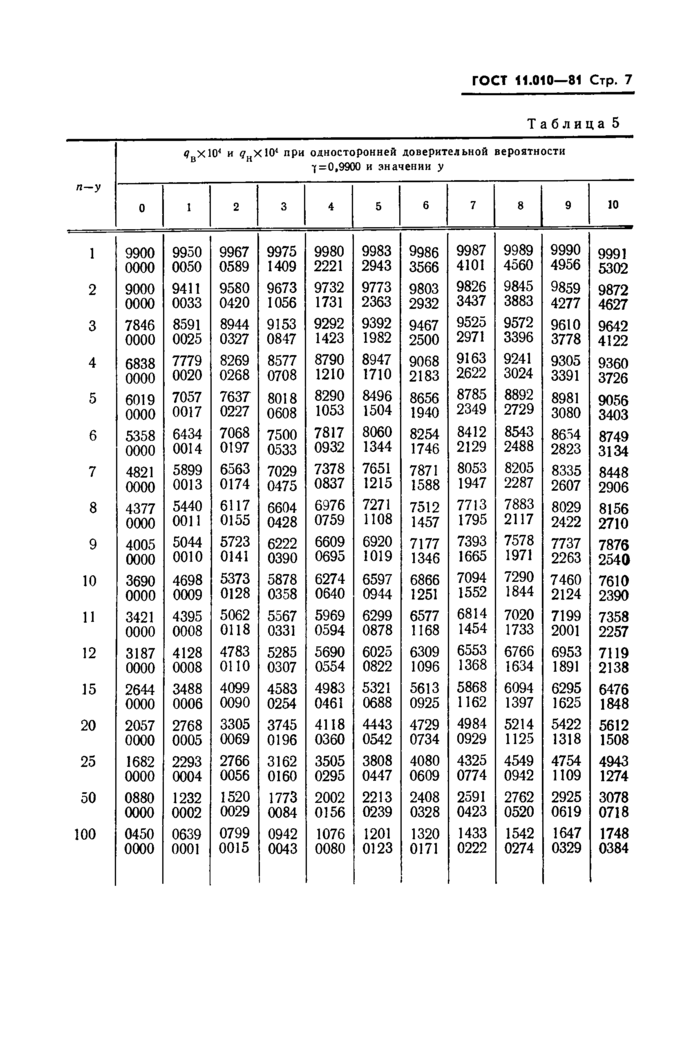
0вХЮ4 и #НХ104 при односторонней доверительной вероятности 7=0,9990 и значении у | |||||||||||
|
п-у |
0 |
• |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
9990 0000 |
9995 0005 |
9997 0184 |
9997 0640 |
9998 1220 |
9998 1814 |
9999 2375 |
9999 2887 |
9999 3349 |
9999 3763 |
9999 4134 |
|
2 |
9684 0000 |
9816 0003 |
9870 0130 |
9899 0476 |
9917 0940 |
9930 1438 |
9940 1927 |
9947 2388 |
9952 2815 |
9957 3207 |
9961 3564 |
|
3 |
9000 0000 |
9360 0003 |
9524 0101 |
9621 0379 |
9684 0767 |
9730 1196 |
9763 1629 |
9790 2046 |
9811 2441 |
9828 2808 |
9842 3149 |
|
4 |
8222 0000 |
8780 0002 |
9660 0083 |
9233 0316 |
9352 0648 |
9438 1025 |
9504 1413 |
9556 1794 |
9598 2159 |
9632 2503 |
9662 2827 |
|
5 |
7488 0000 |
8186 0002 |
8562 0070 |
8804 0270 |
8975 0562 |
9102 0898 |
9201 1249 |
9279 1599 |
9344 1938 |
9398 2262 |
9443 2568 |
|
б |
6838 0000 |
7625 0001 |
8073 0060 |
8371 0237 |
8587 0496 |
8751 0799 |
8880 1120 |
8984 1443 |
9071 1759 |
9143 2064 |
9206 2355 |
|
7 |
6272 0000 |
7113 0001 |
7612 0053 |
7954 0210 |
8206 0444 |
8401 0721 |
8557 1016 |
8684 1316 |
8791 1612 |
8881 1899 |
8959 2176 |
|
8 |
5783 0000 |
6651 0001 |
7185 0048 |
7559 0189 |
7841 0402 |
8062 0656 |
8241 0929 |
8388 1209 |
8513 1487 |
8619 1760 |
8711 2023 |
|
9 |
5358 0000 |
6237 0001 |
6793 0043 |
7192 0172 |
7497 0365 |
7738 0602 |
7936 0857 |
8101 1119 |
8240 1381 |
8361 1639 |
8465 1890 |
|
10 |
4988 0000 |
5866 0001 |
6436 0039 |
6851 0158 |
7173 0338 |
7432 0557 |
7645 0794 |
7824 1041 |
7977 1289 |
8110 1535 |
8225 1775 |
|
11 |
4663 0000 |
5534 0001 |
6109 0036 |
6537 0146 |
6871 0314 |
7143 0517 |
7369 0741 |
7560 0974 |
7724 1209 |
7867 1443 |
7993 1672 |
|
12 |
4377 0000 |
5234 0001 |
5812 0034 |
6246 0135 |
6590 0292 |
6872 0483 |
7108 0694 |
7309 0915 |
7483 1139 |
7635 1362 |
7769 1582 |
|
15 |
3690 0000 |
4495 0001 |
5060 0027 |
5499 0112 |
5856 0242 |
6154 0404 |
6409 0584 |
6630 0774 |
6824 0969 |
6996 1166 |
7149 1361 |
|
20 |
2921 0000 |
3630 0000 |
4151 0021 |
4569 0086 |
4920 0189 |
5222 0317 |
5485 0462 |
5718 ; 0616 |
5926 0777 |
6113 0940 |
6282 1105 |
|
25 |
2414 0000 |
3040 0000 |
3512 0017 |
3901 0070 |
4234 0155 |
4524 0261 |
4782 0382 |
5013 0512 |
5223 0649 |
5413 0788 |
5588 0930 |
|
50 |
1290 0000 |
1671 0000 |
1977 0009 |
2242 0037 |
2479 0081 |
2695 0139 |
2894 0205 |
3078 0278 |
3251 0356 |
3413 0437 |
3566 0520 |
|
100 |
0657 0000 |
0878 0000 |
1052 0004 |
1208 0019 |
1351 0042 |
1484 0072 |
1609 0106 |
1729 0145 |
1842 0187 |
1951 0231 |
2056 0277 |
|
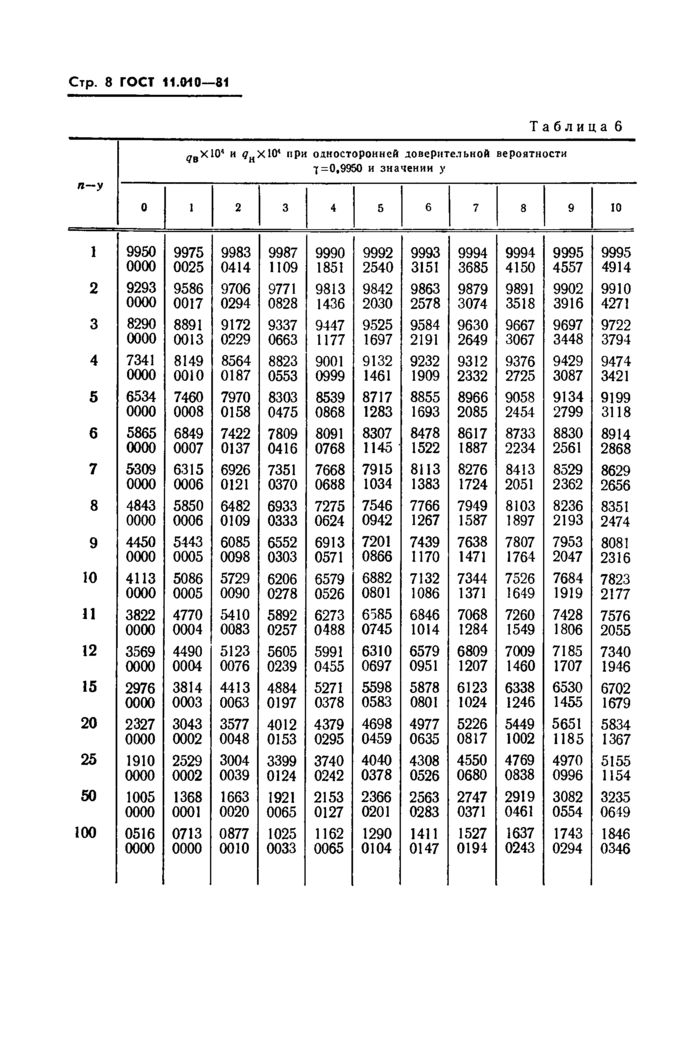
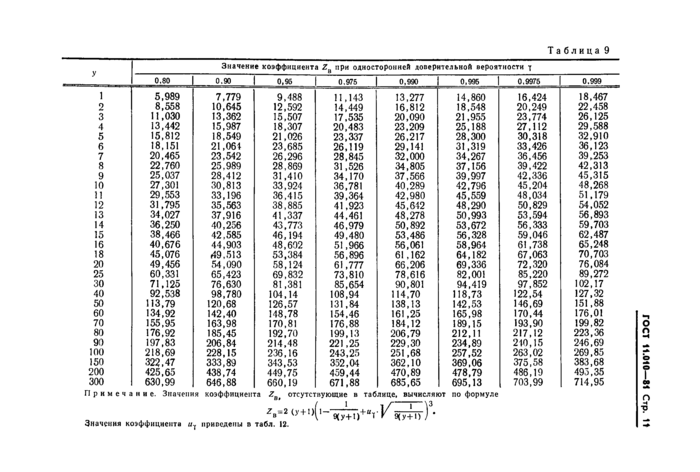
Таблица 9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Примечание. Значения коэффициента ZBi отсутствующие в таблице, вычисляют по формуле | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Z4=2 (>' + 1)(1- 9(у+1)+“Г VэГу+Ту) ■
ГОСТ 11.010-81 Стр. 11
Значения коэффициента и^ приведены в табл. 12.
Стр. 12 ГОСТ 11.010-81
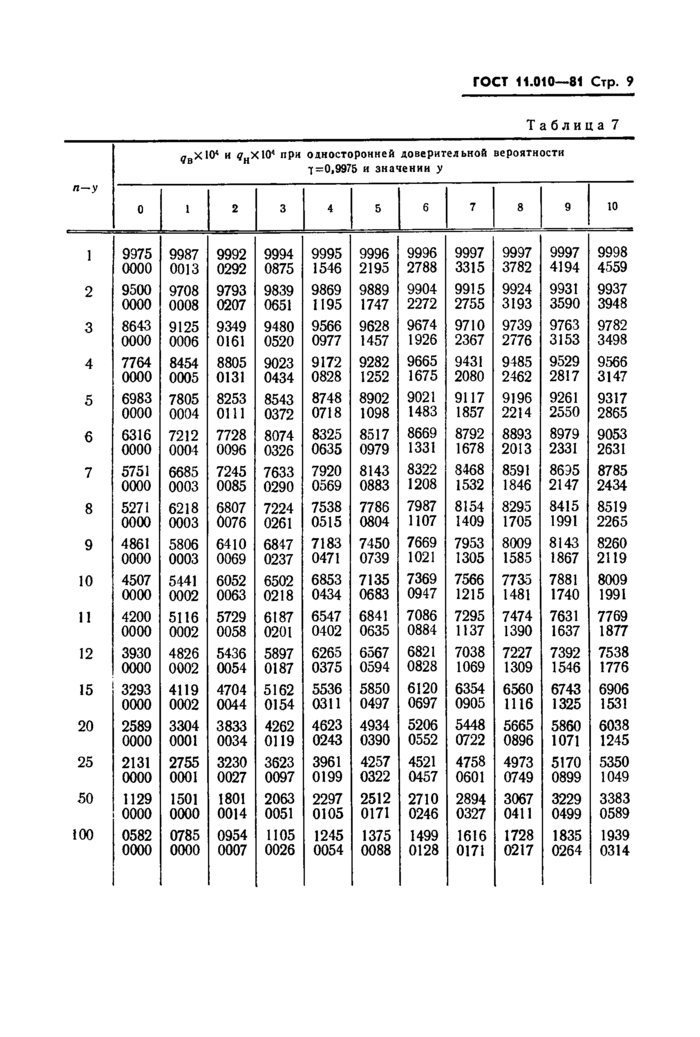
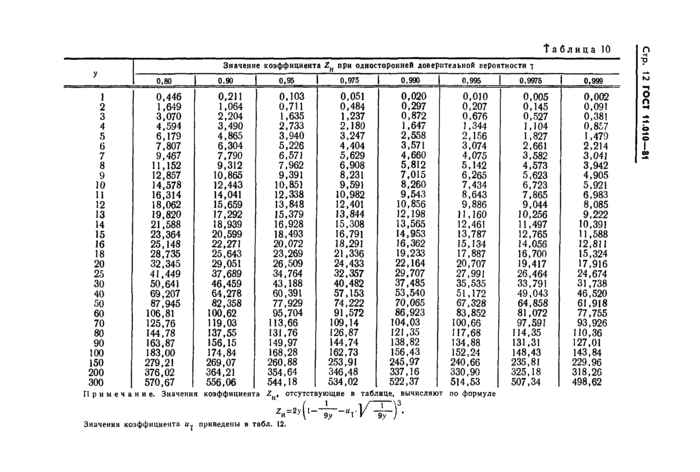
Таблица 10
|
Значение коэффициента ZH при односторонней доверительной вероятности 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
коэффициента Z ( отсутствующие в таблице, вычисляют по формуле приведены в табл. 12. |
ГОСТ 11.010-81 Стр. 13
3.5. В Случае у=0 верхнюю доверительную границу находят по формуле
нижняя доверительная граница qH=0-
3.6. В случае 0<у^п—у доверительные границы qB и qB определяют по формулам:
2 tB+ZB-[2-(y»+2y)+yZB-2*]H6te) ’
2^н+^„—[2(У2—1)+(У—1)^„—ZB]H5tH)’
(6)(7)
где tB = 2n—у, t„=2n—у+1,
а коэффициенты ZB и ZH находят соответственно из табл. 9 и 10 по значениям у и у.
3.7. В случае у>п—у доверительные границы qB и qn определяют по формулам:
9в=1—Рн, (8)
qH=\—pB) (9)
где рв и рн находят в соответствии с пп. 3.3—3.6 как доверительные границы qB и qn, однако значение у заменяют на п—у, а п у на у.
3.8. Доверительные границы рв и рв для параметра р= 1—q находят по формулам (8), (9).
4. ОЦЕНКА ПАРАМЕТРА ОТРИЦАТЕЛЬНОГО БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
4.1. Оценку максимального правдоподобия параметра q отрицательного биномиального распределения (2) вычисляют по формуле
v
Я =
k
k-\~x
(10)
4.2. Несмещенную оценку параметра отрицательного биномиального распределения вычисляют при k^2 по формуле
л к— 1
<7=
к+х—\
(Н)
Стр. 14 ГОСТ 11.010-81
4.3. Оценку максимального правдоподобия (10) используют в следующих случаях:
при значении &=1 для любых значений параметра q\ при значениях £ = 2, 3,..., 22 для q^q*.
Несмещенную оценку (11) используют в следующих случаях: при значениях &>22 для любых значений параметра q\ при значениях k = 2, 3,..., 22 для q<q*\
при k^2 и отсутствии предварительных сведений о величине параметра q.
Значения величины q* для k — 2, 3,..., 22 приведены в табл. 11.
Таблица 11
|
k |
д* |
k |
Q* |
k |
Q* |
|
2 |
0,367 |
9 |
0,548 |
16 |
0,571 |
|
3 |
0,444 |
10 |
0,552 |
17 |
0,573 |
|
4 |
0,483 |
11 |
0,558 |
18 |
0,575 |
|
5 |
0,506 |
12 |
0,561 |
19 |
0,576 |
|
6 |
0,522 |
13 |
0,564 |
20 |
0,577 |
|
7 |
0,533 |
14 |
0,567 |
21 |
0,578 |
|
8 |
0,542 |
15 |
0,569 |
22 |
0,579 |
4.4. Для квадратической функции потерь оценки максимального правдоподобия
R{q)=M{q-q? (12)
несмещенную оценку в случае k^3 вычисляют по формуле A v v v kx (k—i)(k—2)
Я{Я) = {й)2—^Я+^ — (£+*—1 )(£+*—2) • Г3)
4.5. Для квадратической функции потерь (дисперсии) несме* щенной оценки
Л Л
Vq=M{q-q)*
несмещенная оценка при имеет следующий'вид
л л
Vq=
х (k— 1)
(k+x-\)*(k+x-2) ’
(14)
(15)
5. ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРА ОТРИЦАТЕЛЬНОГО БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
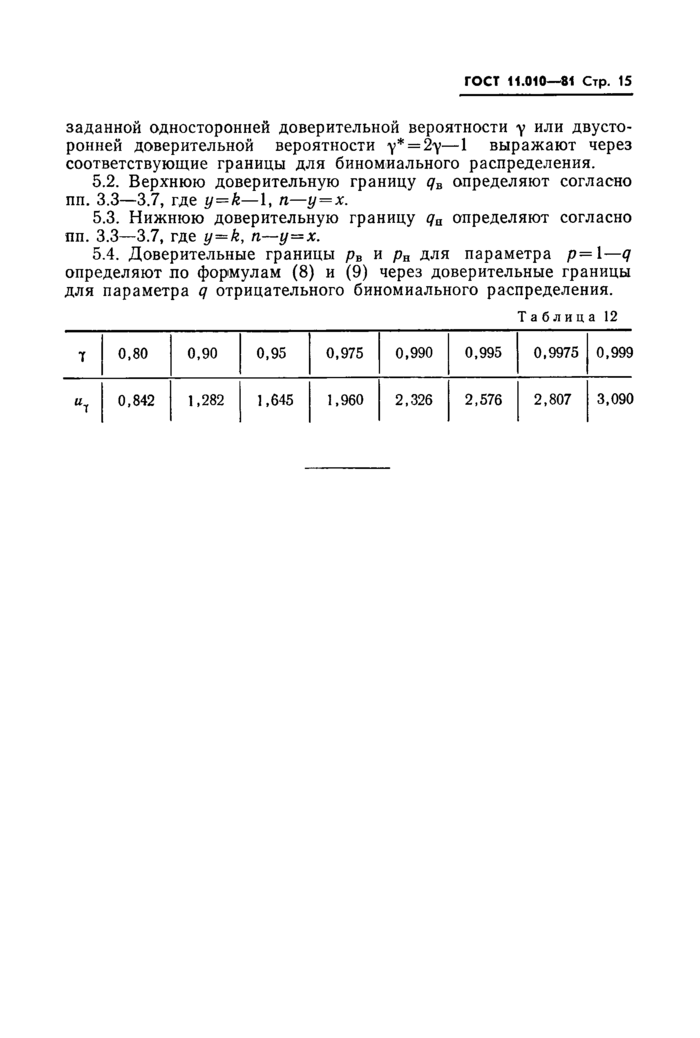
5.1. Верхнюю и нижнюю доверительные границы qB и qs для параметра q отрицательного биномиального распределения при
ГОСТ 11.010--81 Стр. 15
заданной односторонней доверительной вероятности у или двусторонней доверительной вероятности у* = 2у— 1 выражают через соответствующие границы для биномиального распределения.
5.2. Верхнюю доверительную границу qB определяют согласно пп. 3.3—3.7, где y=k—1, п—у = х.
5.3. Нижнюю доверительную границу qa определяют согласно пп. 3.3—3.7, где y=k7 п—у=х.
5.4. Доверительные границы рв и ря для параметра р= 1—q определяют по формулам (8) и (9) через доверительные границы для параметра q отрицательного биномиального распределения.
|
Таблица 12 | ||||||||||||||||||
|
ПРИЛОЖЕНИЕ 1 Справочное
ПРИМЕРЫ ПРИМЕНЕНИЯ ПРАВИЛ СТАНДАРТА
1. Примеры биномиального распределения
Пример 1. При статистическом приемочном контроле качества по одноступенчатому плану в выборке объемом л=250 было обнаружено у=2 дефектных изделий. Требуется оценить входной уровень дефектности q и точность этой оценки.
2
250
Л
Я =
0,0080.
Решение. Используя формулу (3), находим оценку параметра q
2-(250—2) 2502.(250—1)
ЛЛ
0,000031.
Vq=
Точность полученной оценки характеризует несмещенная оценка дисперсии, вычисляемая по формуле (4):
Пример 2. При испытаниях на безотказность 100 изделий отказов получено не было. Найти верхнюю доверительную границу qB для вероятности q отказа изделия за время Т при односторонней доверительной вероятности у=0,95.
Решение. При по табл. 3 для £/=0 и п—у= 100 находим
q& — 0,0295.
Пример 3. По результатам аттестационных испытаний 110 изделий к первому сорту были отнесены 10 изделий, остальные —к высшему сорту. Найти оценку и построить доверительный интервал для вероятности q выпуска изделия первого сорта с доверительной вероятностью у* = 0,90.
Л
я=
10
по
=-0,0909.
Решение. Здесь у= 10, 110. Используя формулу (3), вычисляем оценку
1+Y*
1+0,90
2
0,95.
2
В соответствии с п. 3.2 настоящего стандарта устанавливаем, что у* — 0,90 соответствует односторонняя доверительная вероятность
При y=0>95 по табл. 3 для £/=10, п—г/= 100, пользуясь п. 3.3 находим
Яи = 0,0502, ?в = 0,1493
Пример 4. В условиях примера 2 найти нижнюю доверительную границу для вероятности р безотказной работы изделия за время Т при односторонней доверительной вероятности у=0,95.
Решение. Так как вероятность безотказной работы связана с вероятностью отказа q соотношением р— 1—q, воспользуемся п. 3.8 настоящего стандарта. Согласно примеру 2 верхняя доверительная граница для вероятности отказа </*= 0,0295. Тогда по формуле (8) получаем
ри =1 —?в = 1 -0.0295= 0,9705.
ГОСТ 11.010-81 Стр. 17
Пример 5. При статистическом контроле по одноступенчатому плану в выборке объемом л=200 дефектных изделий обнаружено не было. Найти верхнюю доверительную границу дв для входного уровня дефектности при односторонней доверительной вероятности у=0,99.
Решение. Здесь #=0, п—#=200. При у=0,99 в табл. 5 доверительные границы для пары #=0, п—у —200 отсутствуют. Поэтому значение #в вычисляем согласно п. 3.5 по формуле (5):
200_
<7в=1—0,99 = 0,0288.
Пример 6. При статистическом контроле по одноступенчатому плану в выборке объемом 200 было обнаружено 2 дефектных изделия. Найти верхнюю доверительную границу #в при односторонней доверительной вероятности у=0,99 для входного уровня дефектности q.
Решение. Здесь # =2, л=200. Для #=2, п—#=198 доверительные границы в табл. 1—8 отсутствуют. Учитывая, что в данном примере 0<#<1л—#, поступаем согласно п. 3.6.
Вычисляем tB — 2-200—2=398. По у=0,99 и #=2 в табл. 9 находим коэффициент ZB =16,812. Искомую доверительную границу определяем по формуле (6):
Чв —
_2-16,812_
2-398+16,812—[2 (2а+2-2)+2-16,812—16,8122]/(6 398)
=0,0414.
Пример 7. При аттестационных испытаниях 500 изделий к первому сорту были отнесены 350, остальные — к высшему сорту. Найти доверительные границы #н, qв для вероятности q выпуска изделия первого сорта при односторонней доверительной вероятности у=0,80.
Решение. Здесь #=350, я=500. Для пары #=350, п—#=150 доверительные границы не приведены в таблицах. Так как у>п—#, пользуемся указаниями п. 3.7 и ищем доверительные границы рн и рв для пары #=150, п—# = 350. Поскольку для этой пары значения доверительных границ в таблицах не приведены, а у +0, то поступаем согласно п. 3.6. Вычисляем ^в = 2-500—150=850, *п=2«500—150+1=851. Далее из табл. 9 и 10 соответственно по #=150 и у=0,8 находим коэффициенты ZB=322,47 и ZH=279,21. По формулам (6)—(7) вычисляем рн и рв
Рн —
_2-279,21_
2*850+179,21—[2*(150а—1)+(150—1)*279,212]/(6-851)
-0,2821;
Рв —
_2*322,47_
2-850+322,47—[2-(1502+2* 150)+150*322,47—322,472]/(6-850)
=0,3186.
По формулам (8)—(9) определяем искомые доверительные границы #н и qB. qB= 1—0,3186=0,6814; #в = 1—0,2821 = 0,7179.
Пример 8. Для ускорения процесса испытаний 56 одинаковых полупроводниковых приборов было решено разбить на 4 группы и провести испытания на безотказность за время Т для каждой из групп одновременно. Результаты испытаний зафиксированы в виде таблицы.
|
Номер группы |
1 |
2 |
3 |
4 |
|
Объем группы |
20 |
20 |
10 |
6 |
|
Число отказавших приборов |
3 |
2 |
1 |
2 |
РАЗРАБОТАН Государственным комитетом СССР по стандартам Министерством высшего и среднего специального образования СССР
ИСПОЛНИТЕЛИ
▲. М. Бендерский, канд. техн. наук; Я. П. Лумельский, канд. физ.-мат. наук; А. А. Богатырев, канд. экон. наук; Ю. Д, Филиппов; Л. С. Сипатрина; Н. Г. Миронова; Л. А. Фомина; Н. Е. Бобров; В. В. Чичагов; В. Н. Сенотова
ВНЕСЕН Государственным комитетом СССР по стандартам
Член Госстандарта Б. Н. Лямин
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 30 марта 1981 г. № 1666
Стр. 18 ГОСТ 11.010-81
Требуется по результатам испытаний оценить q — вероятность отказа прибора за время Т и построить верхнюю доверительную границу qB с доверительной вероятностью у = 0,9.
Решение. Здесь в соответствии с п. 1.2 я=20+20+10+6=56,
у=3+2+1+0=6. По формуле (3) находим оценку параметра
А 6
?=-ii-=0’1071-
В табл. 2, отвечающей у=0,90, по значениям у=6 и п—£/=50 находим искомую верхнюю доверительную границу
?в=0,1805.
2. Примеры отрицательного биномиального распределения
Пр и м е р 9. Производится непрерывный статистический контроль партий при нормальном процессе производства до выявления трех забракованных партий. Остановка контроля произошла после проверки 53-й партии. Требуется оценить риск поставщика (вероятность забракования партии), если известно, что q^ 0,2.
А
Ч =
3—1
3+50—1
=0,0385.
Решение. Здесь k—3y х=БЗ—3=50. Из табл. 11 для k=3 находим </*=0,444. Так как q<^0,2<q*, то в соответствии с п. 4.3 пользуемся несмещенной оценкой (11) при оценивании параметра q.
50-(3—1) (3+50-1). (3+50—2)
ЛЛ
=0,0007.
Vq=
Точность полученной оценки характеризует несмещенная оценка дисперсии, вычисляемая по формуле (15):
Пример 10. В условиях примера 9 найти доверительные границы <7Н и q* для вероятности q забракования партии при односторонней доверительной вероятности у=0,9.
Решение. Для определения верхней доверительной границы используем п. 5.2. При у = 0,9 по табл. 2 для пары у=к—1=3—1=2, п—у=х=Ъ0 находим <7в=0,0991.
Нижнюю доверительную границу qH определяем согласно п. 5.3 для пары у—3, п—у=50 также с помощью табл. 2 г7н—0,0210.
Пр и мер II. Проведено 5 серий испытаний на безотказность одинаковых полупроводниковых приборов за время Г. Испытания в i-й серии проводились до получения ki отказов (i'=l, 2, 3, 4, 5).
Исходные данные и результаты испытаний зафиксированы в виде таблицы
|
Номер серии |
1 |
2 |
3 |
4 |
5 |
|
Х1 |
70 |
80 |
100 |
150 |
300 |
|
h |
3 |
3 |
2 |
2 |
8 |
|
Xi |
57 |
77 |
98 |
148 |
292 |
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
Прикладная статистика
ГОСТ
11.010-81
ПРАВИЛА ОПРЕДЕЛЕНИЯ ОЦЕНОК ПАРАМЕТРОВ И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ БИНОМИАЛЬНОГО И ОТРИЦАТЕЛЬНОГО БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЙ
Applied statistics. Point and interval estimators for parameters of binomial and negative binomial distribution
с 01.01 1982 г.
Постановлением Государственного комитета СССР по стандартам от 30 марта 1981 г. № 1666 срок введения установлен
Настоящий стандарт устанавливает правила определения оценок и доверительных границ для параметров биномиального и отрицательного биномиального распределений по совокупности статистических данных, полученных на производстве в процессе измерений, испытаний и анализов, если эти данные подчиняются биномиальному или отрицательному биномиальному распределениям.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Биномиальное и отрицательное распределения имеют место при независимых испытаниях, в каждом из которых с вероятностью <7 появляется событие А.
1.2. Если общее число испытаний п задано, то число испытаний У, в которых появилось событие А, имеет биномиальное распределение.
Для биномиального распределения вероятность принятия случайной величиной У значения у определяется формулой
Р(У=у1д, «)=* (")<7У(1—я)п~у, у=о,1 0)
где
Издание официальное
1.3. Если испытания проводят до появления события А точно k раз, то число испытаний X, в которых событие А не появилось, имеет отрицательное биномиальное распределение.
Перепечатка воспрещена © Издательство стандартов, 1981
Стр. 2 ГОСТ 11.010-81
Для отрицательного биномиального распределения вероятность принятия случайной величиной X произвольного целого неотрицательного значения х вычисляют по формуле
P(X=xjq, к) = (kt±T')-<?k (W)*> ^=°>1 > • • • (2)
Общее число испытаний здесь является случайной величиной
(Х+к).
1.4. В справочном приложении 1 приведены примеры применения правил стандарта, в справочном приложении 2 — теоретические основы стандарта.
2. ОЦЕНКА ПАРАМЕТРА БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
А
2.1. Несмещенная оценка q для параметра q биномиального распределения совпадает с оценкой максимального правдоподо-
д
бия и вычисляется по формуле q=y[n.
л
2.2. Несмещенную оценку дисперсии Vq находят при п^2 по формуле
(4)
ал у-(п~у) Vq~ п*-(п— 1)
3. ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ДЛЯ ПАРАМЕТРА БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
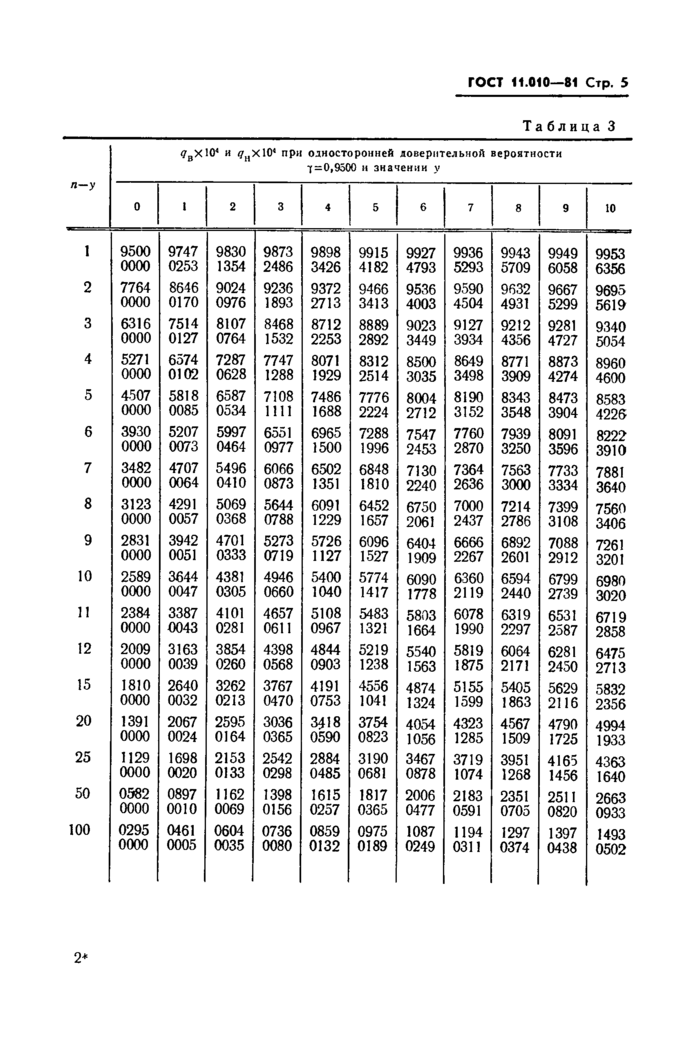
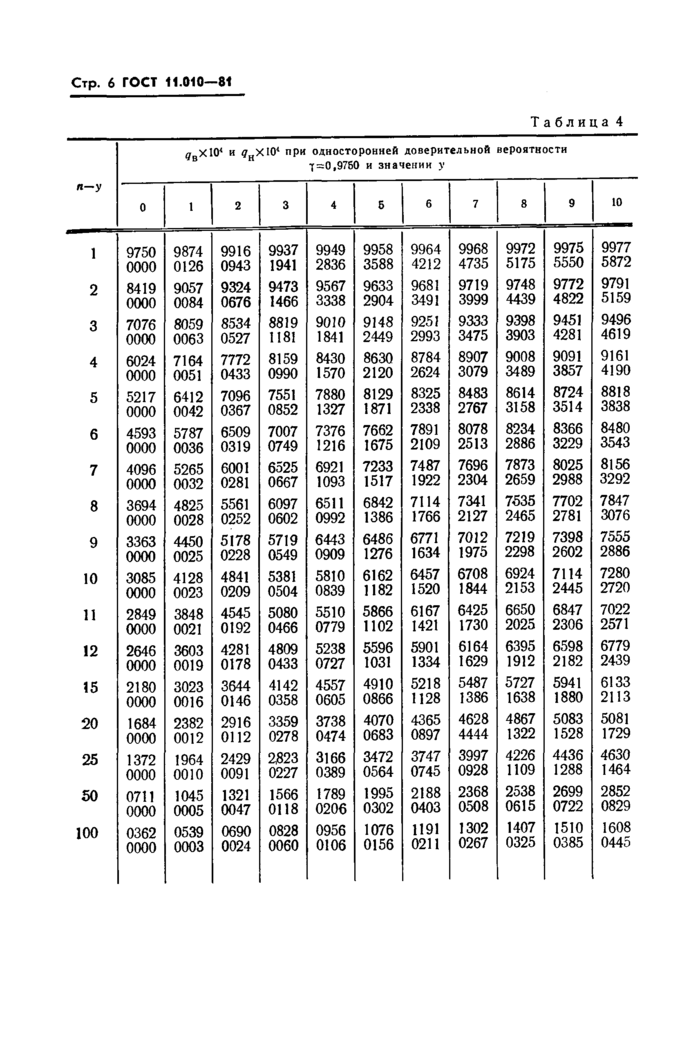
3.1. Верхнюю и нижнюю доверительные границы qB и qH для параметра q биномиального распределения определяют по наблюденному значению у при односторонней доверительной вероятности у из следующего ряда: 0,8000; 0,9000; 0,9500; 0,9750; 0,9900; 0,9950; 0,9975, 0,9990.
3.2. Доверительные границы qH и qB образуют доверительный интервал для параметра q, соответствующий доверительной вероятности у* = 2у—1.
3.3. Доверительные границы qB и qB для параметров биномиального распределения приведены в табл. 1—8 для пар значений у9 п—у (у=0, 1,..., 10; п—у= 1,2,..., 12, 15, 20, 25, 50, 100). Каждая из таблиц отвечает одному из значений у, перечисленных в л. 3.1. В выбранной по значению у таблице паре значений у и п—у соответствуют два числа, верхнее из которых равно 10000 qB9 нижнее— 10000 qn.
3.4. Доверительные границы параметра q в случае значений у и п таких, что пара у и п—у отсутствует в табл. 1—8, определяются согласно пп. 3.5—3.7.
|
Таблица 1 ffBXW4 и £Hxl04 при односторонней доверительной вероятности 7=0,8000 и значении у | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 Зак. 722
|
Таблица 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
<7ВХЮ4 и <7нхЮ4 при односторонней доверительной вероятности 7 = 0,9500 и значении у
|
Таблица 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2*
|
0вХЮ4 и 0НХ1О4 при односторонней доверительной вероятности 7=0,9750 и значении у | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ГОСТ 11.010-81 Стр. 7
|
Таблица 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||