ГОСТ 11.002-73
Прикладная статистика. Правила оценки анормальности результатов наблюдений
Купить ГОСТ 11.002-73 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Устанавливает правила оценки анормальности результатов наблюдений в условиях производства. Требования стандарта должны использоваться при обработке результатов наблюдений случайной величины, заведомо подчиняющейся нормальному закону распределения.
Оглавление
1. Основные положения
2. Критерии оценки анормальности результатов наблюдений при неизвестном генеральном среднеквадратическом отклонении
3. Критерии оценки анормальности результатов наблюдений при известном генеральном среднеквадратическом отклонении и неизвестном генеральном среднем
4. Критерии оценки анормальности результатов наблюдений при известном генеральном среднеквадратическом отклонении и известном генеральном среднем
5. Критерии оценки анормальности результатов наблюдений по модулю их отклонения от среднего
6. Обработка результатов наблюдений по многим выборкам (сравнение частоты появления подозрительных результатов наблюдений
Приложение 1 (рекомендуемое) Примеры применения критериев оценки анормальности результатов наблюдений
Приложение 2 (справочное) Критерии оценки анормальности результатов наблюдений, равноценные приведенным в стандарте
Приложение 3 (справочное) Теоретическое обоснование формул и таблиц, используемых в стандарте
| Дата введения | 01.01.1974 |
|---|---|
| Добавлен в базу | 01.01.2019 |
| Завершение срока действия | 01.03.1987 |
| Актуализация | 01.01.2021 |
Организации:
| 29.09.1972 | Утвержден | Государственный комитет стандартов Совета Министров СССР | 142 |
|---|---|---|---|
| 15.01.1973 | Утвержден | Государственный комитет стандартов Совета Министров СССР | 84 |
| Разработан | ВНИИС | ||
| Издан | Издательство стандартов | 1973 г. |
Applied statistic. Methods of testing of outlying observations
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5
стр. 6

стр. 7

стр. 8
стр. 9
стр. 10

стр. 11
стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17
стр. 18
стр. 19

стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРИКЛАДНАЯ СТАТИСТИКА
ПРАВИЛА ОЦЕНКИ АНОРМАЛЬНОСТИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
ГОСТ 11.002-73 Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СТАНДАРТОВ СОВЕТА МИНИСТРОВ СССР Москва
РАЗРАБОТАН Всесоюзным научно-исследовательским институтом стандартизации (ВНИИС)
Директор д-р экон. наук Гличев А. В.
Научный консультант д-р техн. наук. проф. Шор Я. Б.
Научный руководитель канд. техн. наук Бендерский А. М.
Исполнители: канд. техн. наук Лосицкий О. Г„ Филиппов Ю. Д., Воробьева В. К.
ВНЕСЕН Всесоюзным научно-исследовательским институтом стандартизации (ВНИИС)
Директор д-р экон. наук Гличев А. В.
ПОДГОТОВЛЕН К УТВЕРЖДЕНИЮ Техническим управлением Государственного комитета стандартов Совета Министров СССР
Начальник отдела общетехнических стандартов Талашов В, А.
Ст. инженер Распевакина Н. Т.
УТВЕРЖДЕН Государственным комитетом стандартов Совета Министров СССР от 29 сентября 1972 г. (протокол № 142)
Председатель отраслевой научно-технической комиссии зам. председателя Госстандарта СССР Ткаченко В. В.
Члены комиссии: Лямин Б. Н., Панфилов Е. А., Шаронов Г. Н., Гличев А. В., Верченко В. Р., Бурденков Г. К., Киселев Б. Р.
ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета стандартов Совета Министров СССР от 15 января 1973 г. № 84
ГОСТ 11.002-73 Стр. 9
6. ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПО МНОГИМ ВЫБОРКАМ (СРАВНЕНИЕ ЧАСТОСТИ ПОЯВЛЕНИЯ ПОДОЗРИТЕЛЬНЫХ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ С ВЕРОЯТНОСТЯМИ а И а*]
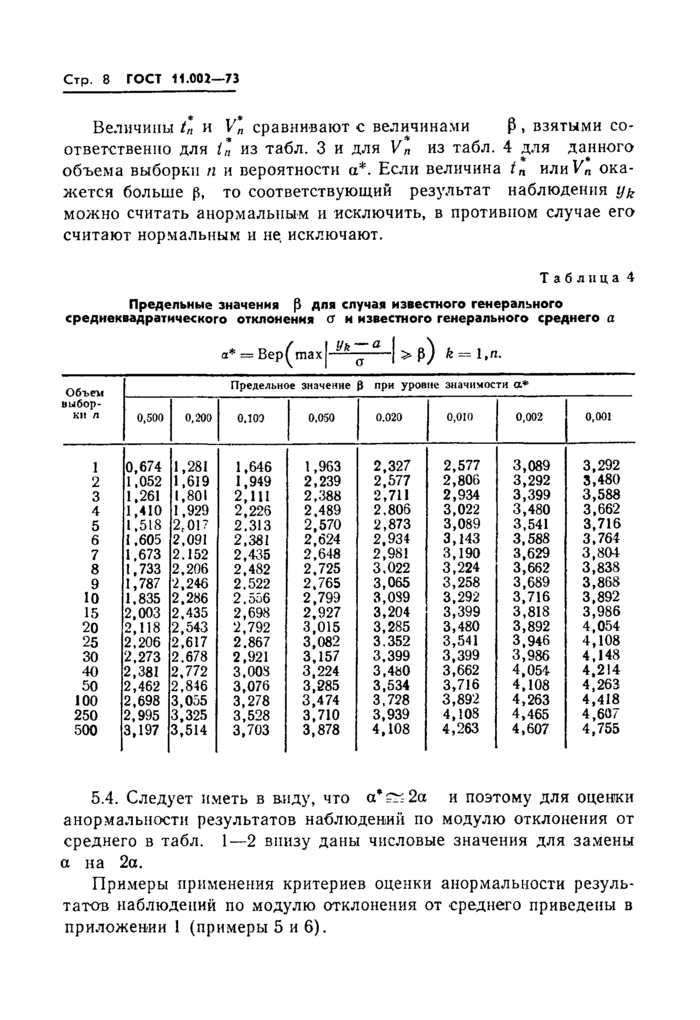
6.1. В некоторых случаях при обработке результатов наблюдений ставят задачу оценить анормальность результатов при условии, что имеете^ N выборок объемом п каждая и в т из них содержится по одному результату, вероятность которого в выборке как нормального равна а . Для решения этой задачи следует убедиться в том, что выборки независимые. Затем вычисляют вероятность того, что по крайней мере в т выборках из N будут результаты наблюдений, вероятность которых как нормальных равна а. Эту вероятность вычисляют по формуле
RN.m= 2 (^)а‘
i~m
^приближенные значения К^,т приведены в табл. 5). Если она окажется малой величиной, то подозреваемые результаты можно считать анормальными и исключить, в противном случае их считают нормальными и не исключают.
Стр. 11
ПРИЛОЖЕНИЕ 1 к ГОСТ 11 М2—73 Рекомендуемое
ПРИМЕРЫ ПРИМЕНЕНИЯ КРИТЕРИЕВ ОЦЕНКИ АНОРМАЛЬНОСТИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИИ
Пример 1* Определяют твердость образцов металла стальным шариком (по Брннеллю). При этом получено пять значений твердости: НВ 180, НВ 182,
НВ 183!, НВ 184, НВ 196.
Требуется оценить результатов 196 при заданном « =Q/)50.
Для критерия ип = -п~У вычисляют
_ 180+ 182 + 183 + 184 4- J 96
У=-5-= 185.
S = -[-{(180 — 185)2 + (182 — 185)2 + (183—185)2 -f (184—185)“+
откуда
196— 185 6,3
— 1,75.
ип =
+ (196-185)“} =6,3,
В табл. 1 настоящего стандарта для п—5 и а —0,050 находят f>=l,67.
Тотда Un > р и результат НВ 196 можно считать анормальным и исключить. Более того, такой вывод можно сделать с большей вероятностью, так как при 5 и а — 0,025 3 =1,72.
Необходимость тщательного подхода к оценке анормальности можно показать на другом примере, в котором выборочные результаты наблюдений мало отличаются от приведенного.
Пример 2. Была получена твердость пяти деталей: НВ 178, НВ 180, НВ 184, НВ 186, НВ 197.
Вычисляют
я
178 4- 180 + 184 4- 186 + 197 У —-g-= 185;
^-{(178 - 185)3 -f- (180—185)2 ~f- (184 — 185)2 + (186—185)* + + (197 - 185)2}= 7,4,
откуда
= 1,62.
197-185
В этом случае U(1,67) для п—Ь и а =0,050 и, следовательно, для исключения результата НВ 197 нет оснований.
Пример 3. Испытывают пробегом выборку 10 шнн. Получены следующие результаты пробега до полного износа в км: 65000, 66100, 65700, 65800, 66500,
67000, 64700, 65000, 64000, 60200. Генеральное среднеквадратическое отклонение ст *=970 км.
Требуется оценить результат 60200 км при заданном а = 0.00^
Вычисляют
65.0+66,1+65,7+65.8+66.5+67,7+64,7+65,0+64,0+60,2 У =--Jo-= 65,0;
'i =
60,2 — 65,0 0,97
= -4,948,
В табл. 2 настоящего стандарта для ге=10 и а =0,005 находят Р =3,122. Поскольку t\<—fi, то для заданных условий можно считать результат #1=60200 км анормальным и исключить.
Пример 4. Оценка анормальности при известном генеральном среднеквадратическом отклонении и известном генеральном среднем (см. 4.1).
Для проверки стабильности технологической операции обточки вала в течение заданного времени была извлечена выборка 12 валов диаметрами (мм): 40,00; 40,02; 39,99; 39,98; 40,00; 40,03; 39,99; 39,98; 40,01; 40,08; 40,04; 39,97.
Генеральное среднеквадратическое отклонение о =0,024, генеральное среднее а=40,00, требуется оценить результат 40,08.
Вычисляют
40,08 — 40,00 Vn~ 0,024 - 3,33.
Путем линейного интерполирования в табл. 3 для л=12 и « =0,005 находят Р =3,346. Отсюда вероятность того, что результат 40,08 принадлежит данной нормальной совокупности мала (а =0,005), поэтому его .можно считать анормальным и исключить.
Пример 5. При определении плотности электролита в относительных единицах получены следующие результаты X: 215; 210; 210; 201; 217; 215;
215; 214; 209; 217; 228.
Подозревают в анормальности результаты 201 и 228. Требуется оценить их по модулю отклонения от среднего.
Вычисляют
215+2104-210+201+217+215+215+214 4-209+217+228 X--Y\- “ 212,9;
5 = +{(2,1)*+( -2,9)*+(-2,9)*+(-11,9)* +
+ 4,1*4-2,1*+2,1* + 1,1* + (-3.9)*+ 4,1*+ 15,1*} = 6,7,
откуда
Ь
*
п
1228 — 212,9 I 6,7
2,25.
В табл. 1 настоящего стандарта для я=11 значениям р*=2,36 и Р =*2,23 соответствуют вероятности =0,025 и =0,050. После интерполирования их с вероятностью «*=0,092 приходят к выводу, что результаты можно считать нормальными н для исключения их нет оснований. Оценку Х=201 производят аналогично.
Пример 6. Микроизмерения штриха на масштабе дали следующие результаты;
| ||||||||||||||||
|
известной о=1,0 |
3,68 2,95 3,27 2,48
Точность этих измерений характеризуется оценить анормальность результатов 1,81 и 6,35.
Требуется
Стр. 13
Х=-А- 2 Xt = 3,893; n f=I
|
tn = max |
6,35 — 3,89 i |
= 2,46.
Из табл. 2 настоящего стандарта видно, что при п=20 и нормальных условиях это значение имеет вероятность а >0,20, поэтому считать его анормальным нет оснований. Оценку результата 1,81 производят аналогично.
Пример 7. При съемке местности для нанесения рельефа на топографическую карту было получено 100 выборок по восьми измерений в каждой. В трех выборках было по одному измерению уп такому, что
у„ — У
>/2ЛЗ*
Трйбуется оценить анормальность этих результатов.
Из табл. 1 настоящего стандарта следует, что при п=8 и Un —2,13 а —0,025. При этой вероятности вероятность того, что по крайней мере в шести выборках из 100 будут иметь место указанные результаты равна:
/?100.б = S° (}°°) 0.025'( I-0.025)100 - ' .
/=6
Имея в виду, что для N=100 и а=0,025 биномиальное распределение хорошо аппроксимируется распределением Пуассона с параметром * = Na=
= 100-0,025=2,5, это выражение можно заменить:
Л 100
R1С0, б — е ' 2*
1=0
(2,5)*
И
— \—с
-2,5
1=0
г!
По таблице распределения Пуассона определяют для *=2,5 и т=6
6
о г (2,5У в-2,5 s > = 0,9805 и
Н 11
^юо.б “ 0,0195.
Вследствие малой вероятности #10о,б есть основания считать результаты уп анормальными и исключить их.
Подобный вывод был бы неправильным, если бы в двух выборках из 100 встретились результаты наблюдений, вероятность которых как нормальных а =0,025.
В этом случае вероятность
R100 6 = \-е~2'5 S (2;.,5) =1—0,5499 = 0,4501
достаточно велика и для исключения указанных результатов нет оснований.
Стр. 14
ПРИЛОЖЕНИЕ 2 к ГОСТ 11.002-73 Справочное
КРИТЕРИИ ОЦЕНКИ АНОРМАЛЬНОСТИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ, РАВНОЦЕННЫЕ ПРИВЕДЕННЫМ В СТАНДАРТЕ
1. Наряду с критериями анормальности, приведенными в стандарте, имеются равноценные им. Применение этих критериев правомерно так же, как лриве-денных в разд. 2 и 3 настоящего стандарта.
2. Вместо критерия анормальности
ип
Уп—У
S
может быть использован критерии
U.
Уп ~~ Уп-1
в котором
Уп-\
1
л —I
л-1
s УП /=1
I л-1
—Ц X (у/
Л — 2
|
У/1—1 |
т. е. у и S л—1 подсчитаны по всем результатам наблюдений, за исключением результата, подозреваемого в анормальности.
В этом случае величину Uп следует сравнивать с величиной р, взятой из.
табл. 1, л принимать решение тем же путем, что и в случае с Un .
Оценка результата у\ с помощью критерия
Ух—Ух Sx
в котором у\ п Si подсчитаны по всем результатам наблюдений, за исключением подозреваемого в анормальности у\, производится аналогично.
Доказательства равноценности критериев Un и U'n (U\ и U\) приведены в приложении 3.
3. Вместо критерия оценки анормальности tn можно использовать критерий
анормальности
Уп-Уп-1
в котором
\ л—1
—Ц- X yh п — 1 /=1
т. е. выборочное среднее для выборки без подозреваемого в анормальности результата наблюдения уп.
В этом случае полученное значение tn следует сравнить с величиной Завзятой из табл. 2, и действовать точно в соответствии с требованиями раэд. 3 настоящего стандарта.
Стр. 15
Оценка анормальности результата наблюдения ух с помощью критерия
/' _ Ух~Ух 1 ~ о •
в котором
I
п
2 yj
П — 1 ;=2‘
производится аналогично.
Следует иметь в виду, что оба критерия tn и /'rt и tx) равноценны.
4. Примеры применения равноценных критериев
4.1. В примере 1 приложения 1 установлено, что вероятность результата НВ 196 как нормального не более а =0,025 и поэтому его можно считать анормальным и исключить.
Такой же вывод получается при применении критерия U п .В этом случае для оценки твердости металла следует принять
- 1804-182+183+184
»п-1 = -4-!-= 182-2-
5„_, 4-{(180—182.2)2+(182—182,2)а + (183—182,2)» +
откуда
U,
+ (184- 182,2)а} = 1,67, 196,0- 182,25
л— 1,67 что больше 6,509 при п—5 и « =0,025 (см. табл. 1).
4.& В примере 2 приложения 1 установлено, что для исключения результата НВ 197 нет оснований.
Точно такая же оценка получается при использовании критерия Uп по табл. 1.
Выше уже подсчитаны
уп-х*=т,2 и 5л—1=1,67,
тогда
196 -182,2 Unt= 1,67 —
что больше р =5,086 для л=5 и «=0,050 (см. табл. 1).
Для второй рассмотренной выборки получается
178+180+184+186 t Уп-1 = -4-= 182.
5
откуда
= }/*4"{( 178-182)2 + ( 180—182)2+( 184-182)а+(186-182)2} = 3,65„
197 — 182
U.
4,1;
Л 3,65
что меньше р=5,086. Как и следовало ожидать, выводы при использовании критериев Un и и'п получились одинаковые.
4.3. В примере 3 приложения 1 установлено, что результат ух=60200 км можно считать анормальным и исключить его.
К такому же выводу приходят при использовании критерия tx *
- 65,0+66,1+65.7+ 65,8+66.5 + 67,0+64,7+65,0+ 64.0 м
Ух =-о-=65,7
Это меньше, чем — S = ^3(467.
9
60.2 — 65,7 0,97
5,650.
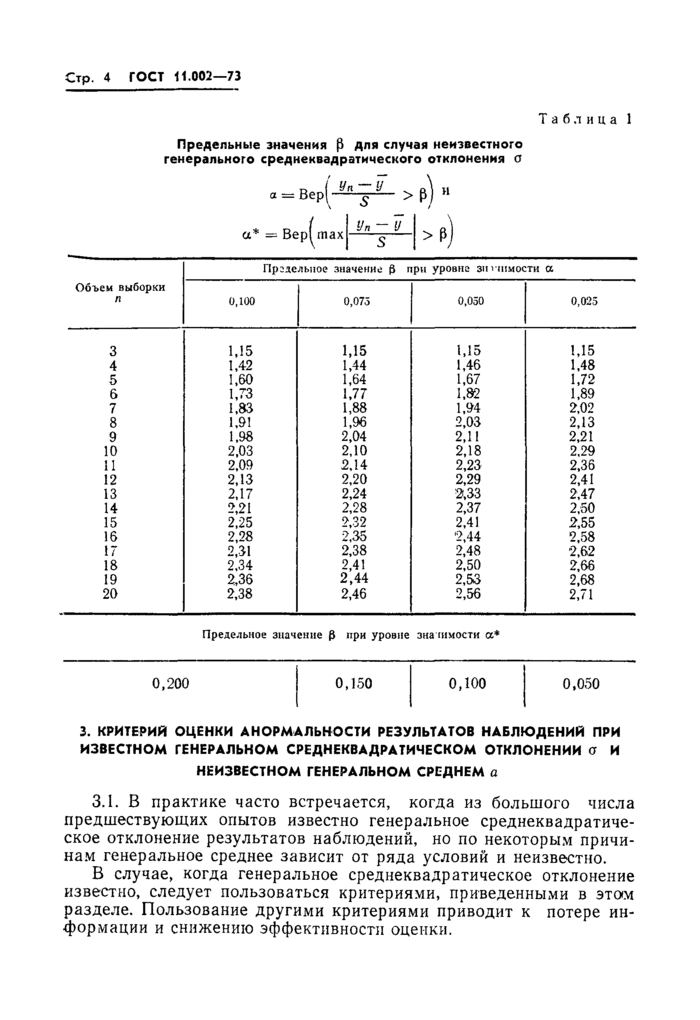
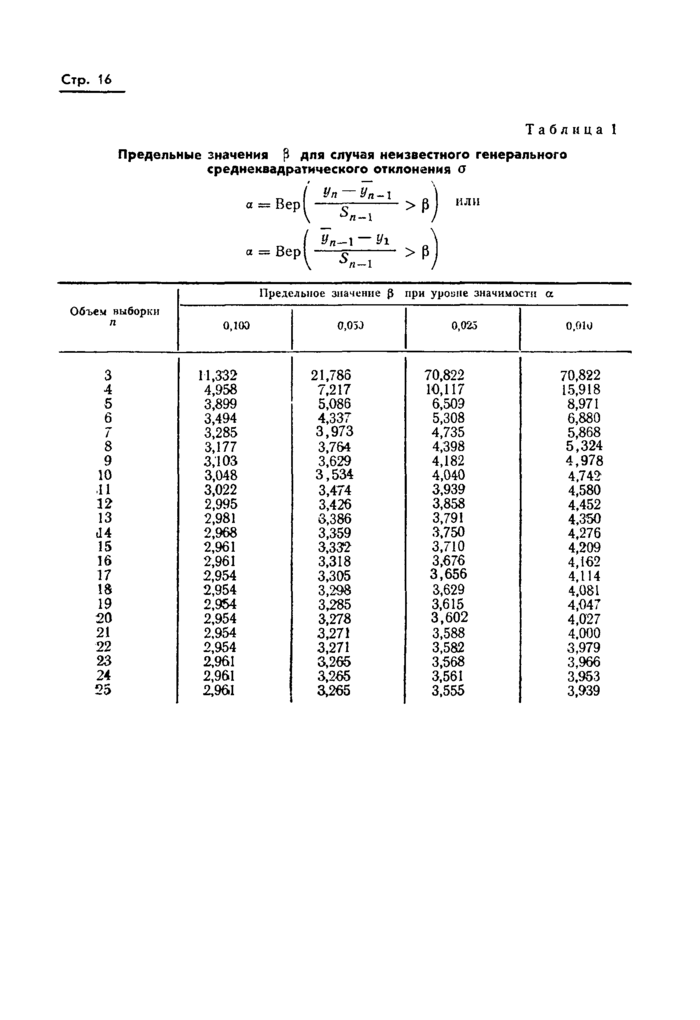
Таблица 1
Предельные значения р для случая неизвестного генерального среднеквадратического отклонения а
а — Вер
|
Уп-Уп-1 $п-\ |
или |
Уд-1 - У г
$п-1
> р
|
а = Вер | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
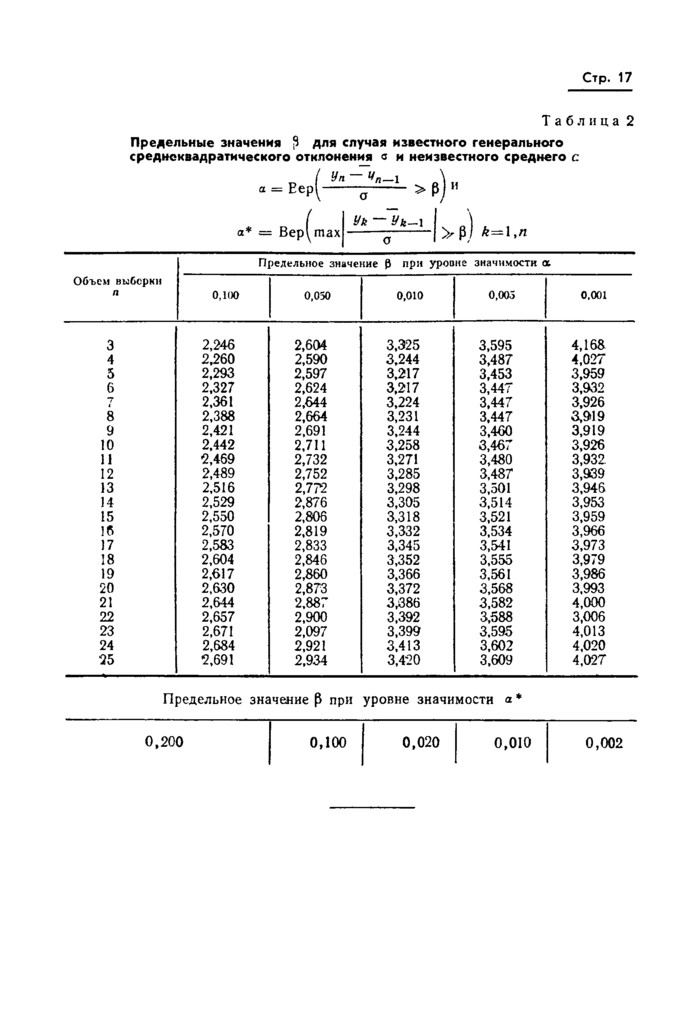
Стр. 17
Таблица 2
Предельные значения Э для случая известного генерального среднеквадратического отклонения о и неизвестного среднего с
а
Еер
Уп ~ (/„1 а
>р г
|
а* = Bepl max Ук — Уь~ 1 а Ar=l,/i | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0,200
0,100
0,020
0,010
0,002
Стр. 18
ПРИЛОЖЕНИЕ 3 к ГОСТ 11.002-73
Справочное
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ФОРМУЛ И ТАБЛИЦ, ИСПОЛЬЗУЕМЫХ В СТАНДАРТЕ
1. Впервые правильное решение задачи об оценке анормальных результатов наблюдений было дано Н. В. Смирновым в 1941 г. В 1950 г. Ф. Е. Груббе повторил результат Н. В. Смирнова без ссылки на него [3]. Поэтому в литературе часто неправомерно критерий Н. В. Смирнова приписывается Ф. Е. Груббсу. Существовавшие до 1941 г. критерии оценки анормальности, в том числе известный критерий Шовенэ, оказались либо пригодными только в некоторых частных случаях, либо вообще научно необоснованными и непригодными для использования. Подробный анализ и критика указанных критериев приведены в [2].
В 1952 г. А. М. Бендерский распространил критерий Н. В. Смирнова на случай оценки модуля максимального отклонения от среднего в ряду наблюдений [4]. Обзор дальнейших работ по оценке анормальности наблюдении приведен в [5].
В последнее время появились работы [8—1 Б] по вопросу принятия решений об оставлении или исключении подозреваемых в анормальности результатов наблюдений в зависимости от дополнительных данных, выражающих функцию риска ошибочных решений. Выводы, сделанные в этих работах, в стандарт не включены ввиду их дискуссионного характера.
2. Вывод критерия Н. В. Смирнова (см. таблицы в [1, 2, З1, 6]).
Рассматривается выборка независимых случайных величин из генеральной
нормальной совокупности (0, с ) с известной дисперсией а2
Хи Х„ (1)
и получающаяся из нее упорядоченная выборка
У1< . ■ . < Уп, где Xi = У}. (2)
Требуется определить распределение вероятности величины
|
ип = |
2 (г/у— у)
/=!
(3)
Лри указанных выше условиях величина
Нk — £ (* — 1
(4)
1 п __
* В связи с тем, что при S2 =-2 (X; — X)2 получаются более ком-
п 1=1
.пактные выражения для границ интервалов и рекуррентного соотношения при теоретическом рассмотрении, цринято такое выражение вместо
7 2 (Xi-Xf 1 i=i
УДК 658.562.012.7(083.74) Группа Т59
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ГОСТ 11.002—73
Прикладная статистика ПРАВИЛА ОЦЕНКИ АНОРМАЛЬНОСТИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
Applied statistic. Methods of testing of outlying observations
Постановлением Государственного комитета стандартов Совета Министров СССР от 15 января 1973 г. № 84 срок введения установлен
с 01.01.1974 г. до 01.01.1979 г.
Настоящий стандарт устанавливает правила оценки анормальности результатов наблюдений в условиях производства. Требования стандарта должны использоваться при обработке результатов наблюдений случайной величины, заведомо подчиняющейся нормальному закону распределения.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Анормальным называется результат наблюдения, резко отклоняющийся от группы результатов наблюдений, которые являются нормальными.
1.2. При оценке анормальных результатов наблюдений следует рассмотреть альтернативу:
резко отклоняющийся результат наблюдения получен в тех же условиях, что и остальная группа результатов наблюдений, принадлежит к той же генеральной совокупности, но вероятность получения его мала. В этом случае оцениваемый результат наблюдений не следует исключать и расчет выборочных характеристик для оценки параметров генеральной совокупности (средняя и дисперсия) должен производиться с учетом всех без исключения результатов наблюдений;
Перепечатка воспрещена
резко отклоняющийся результат наблюдения вполне мог бы быть следствием случайного нарушения нормальных условий или грубых ошибок при наблюдении или расчете. В этом случае указанный результат наблюдений не принадлежит той же генеральной совокупности, что и остальные, поэтому он может быть исключен из общей выборки. Тогда расчет выборочных характеристик
Издание официальное
© Издательство стандартов, 1973 г.
Стр. 19
имеет распределение с плотностью вероятностей
, r(i^)
<p(tf) =
п — 4
Vn(n — l)
(5)
Вероятность того, что значение Un будет заключено в пределах U, U+dUy равна вероятности того, что одно из отношений U* будет в этом интервале {<p (U)dU]t умноженное на условную вероятность того, что остальные «— 1 значений U i будут меньше U % и умноженное на число способов, которыми может •быть получено Un.
Вер {U <Un<U + dU} = nPn_x(U)i¥(U)dU. (6)
Для краткости можно записать:
Bep(t/j, . . . 1/}=Рл_1(У). (7)
В [2] подробно показано, что — 1 ив интервалах
/_ _
7^. ^/~в ~ 2--вероятность Р п_2 (t/) = 1 (8)
|/"” ~4 . )/~~ 3 —вероятность Р„_3 (*У) = 1
п — 2
|/“п — 1
вероятность Я n_i (U) — 1
В [2] показано, что существует рекуррентное соотношение
в(У) = /^гг 17=%===>
(9)
при котором в интервале
(10)
юят-
(П)
(12)
вероятность (U) того, что Uп_х<и при условии Un~U равна вероят
ности того, что
где
^л—1 У п — 1
'л—1
тогда
л—1
Уп-1 =
2 у,*:
т, е.
б(С/)
(13)
Стр. 2 ГОСТ 11.002-73
для оценки параметров генеральной совокупности должен производиться по выборке, из которой исключен анормальный результат наблюдения.
1.3. Следует иметь в виду, что решение такой задачи в любом случае с определенной малой вероятностью можегг оказаться ошибочным:
а) принимается решение о том, что подозреваемый результат наблюдения нормален и он оставляется, в то время как в действительности он анормален и подлежит исключению;
б) принимается решение об исключении результата наблюдения как анормального, в то время как он нормален и его следует оставить.
Поэтому при принятии решения об исключении или сохранении резко отклоняющихся результатов наблюдений нужно проявлять большую осторожность и перед этим внимательно анализировать условия, в которых получился резко отклоняющийся результат наблюдения.
1.4. Когда определенно известно, что резкое отклонение одного из результатов наблюдений возникло при воздействии факторов, не свойственных условиям получения остальных результатов наблюдений, следует исправить этот результат пересчетом его для условий, при которых исключается несвойственный фактор. Если такой прием оказывается невозможным, то надо обратиться к методам статистической оценки.
Этими же методами необходимо пользоваться и в тех случаях, когда причина резкого отклонения одного из результатов наблюдений от остальных в условиях эксперимента остается незамеченной.
1.5. Принцип решения вопроса об анормальности заключается в том, что по результатам наблюдений рассчитывается определенная функция от случайной величины, для которой известно распределение вероятностей. Вычисленное по выборочным данным значение этой функции сравнивается с ее предельным значением, соответствующим заранее принятой малой вероятности. Если при этом выясняется, что вероятность подозреваемого в анормальности результата наблюдений меньше принятой, то выносится решение о том, что оцениваемый результат анормальный и подлежит исключению, в противном случае его считают нормальным и не исключают.
1.6. При выборе критерия оценки анормальности результатов наблюдений надо руководствоваться следующими принципами:
а) используемые в настоящем стандарте методы и критерии оценки предполагают нормальное распределение измеряемой величины. Поэтому предварительно экспериментатор должен тщательно оценить возможность принятия гипотезы нормального распределения;
б) надо всегда иметь в виду, что результаты обработки наблю-
ГОСТ 11.002-73 Стр. 3
дений будут тем точнее, чем больше информации будет использовано. Поэтому, когда известно генеральное среднеквадратическое отклонение или когда оно может быть найдено в результате обработки предшествующих опытов, следует пользоваться критериями* основанными на использовании известного среднеквадратического отклонения. И только когда оно неизвестно и нет возможности его получить на основании предшествующих опытов, следует пользоваться критериями, основанными на использовании выборочного среднеквадратического отклонения.
1.7. Критериям анормальности, приведенным в стандарте, равноценны критерии, приведенные в приложении 2.
1.8. Теоретическое обоснование критериев рассмотрено в справочном приложении 3.
2. КРИТЕРИИ ОЦЕНКИ АНОРМАЛЬНОСТИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПРИ НЕИЗВЕСТНОМ ГЕНЕРАЛЬНОМ СРЕДНЕКВАДРАТИЧЕ.СКОМ ОТКЛОНЕНИИ о
2.1. Для упорядоченной выборки результатов наблюдений случайной величины
У1<Уг<- ■ ■ 'У.,
подсчитывают выборочное среднее
у=—Ху< (1)
" г=1
и выборочное среднеквадратическое отклонение
<2)
Чтобы оценить принадлежность уп или у\ к данной нормальной совокупности и принять решение об исключении или оставлении Уп{У\) в составе выборки, находят отношение
Un = Уп~1- или £/,= У~У1 . (3)
Результат сравнивают с величиной Р, взятой из табл. 1 для данного объема выборки п и принятого уровня значимости а.
Если Un У/ Р, то подозреваемый в анормальности результат наблюдения анормален и может быть исключен, в противном случае его считают нормальным и не исключают.
Оценка результата наблюдения у\ производится аналогично.
Примеры применения критериев оценки анормальности результатов наблюдений при неизвестном среднеквадратическом отклонении приведены в приложении 1 (примеры 1 и 2).
Таблица 1
Предельные значения р для случая неизвестного генерального среднеквадратического отклонения с
|
а* |
|
и |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Предельное значение (S при уровне значимости а* | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0,200
0,150
0,100
0,050
3. КРИТЕРИЙ ОЦЕНКИ АНОРМАЛЬНОСТИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПРИ ИЗВЕСТНОМ ГЕНЕРАЛЬНОМ СРЕДНЕКВАДРАТИЧЕСКОМ ОТКЛОНЕНИИ <7 И НЕИЗВЕСТНОМ ГЕНЕРАЛЬНОМ СРЕДНЕМ а
3.1. В практике часто встречается, когда из большого числа предшествующих опытов известно генеральное среднеквадратическое отклонение результатов наблюдений, но по некоторым причинам генеральное среднее зависит от ряда условий и неизвестно.
В случае, когда генеральное среднеквадратическое отклонение известно, следует пользоваться критериями, приведенными в этом разделе. Пользование другими критериями приводит к потере информации и снижению эффективности оценки.
ГОСТ 11.002-73 Стр. 5
3.2. Для упорядоченной выборки результатов наблюдений
0i<0><- • •<0я
подсчитывают выборочное среднее
0 = дг2 0*
и вычисляют отношение
которое сравнивается с величиной Р, взятой из табл. 2 для данного объема выборки п и принятой вероятности а.
Таблица 2
Предельные значения р для случая известного генерального среднеквадратического отклонения о и неизвестного среднего а
|
а = Вер(> р), а = Вер^ У > р) и а* — Bep^maxj--*-— У | > р) k=\,n | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Предельное значение 0 при уровне значимости а* | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если tn У/ р , то результат наблюдения уп анормален и может быть исключен, в противном случае его считают нормальным и не исключают. Оценка анормальности результата наблюдения у\ производится аналогично.
Пример применения критерия оценки анормальности результатов наблюдений при известном генеральном среднеквадратическом отклонении и неизвестном генеральном среднем приведен в приложении 1 (пример 3).
4. КРИТЕРИЙ ОЦЕНКИ АНОРМАЛЬНОСТИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПРИ ИЗВЕСТНОМ ГЕНЕРАЛЬНОМ СРЕДНЕКВАДРАТИЧЕСКОМ ОТКЛОНЕНИИ а И ИЗВЕСТНОМ ГЕНЕРАЛЬНОМ СРЕДНЕМ а
4.1. В практике такой случай встречается, когда надо проверить, что генеральная совокупность, из которой извлечена выборка, имеет среднее а при условии, когда известно генеральное среднеквадратическое отклонение о .
4.2. Для оценки анормальности результата наблюдений уп, где
У1<У2< ■ ■ ■ <Уп,
подсчитывают величину
Гя=3£-^£_. (о)
Величину Vn сравнивают с величиной |3, взятой из табл. 3 для принятой вероятности.
Если V пуур , то уп можно считать анормальным и исключить из выборки, в противном случае его считают нормальным и не исключают.
Оценка анормальности результата наблюдения у\ производится аналогично.
Пример применения критерия анормальности при известном генеральном среднеквадратическом отклонении и генеральном среднем приведен в приложении 1 (пример 4).
Таблица 3
Предельные значения р для случая известного генерального среднеквадратического отклонения о и известного генерального среднего а
|
а = Вер( а > р) или я = Вер(~-^ > р) | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
|
Продолжение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
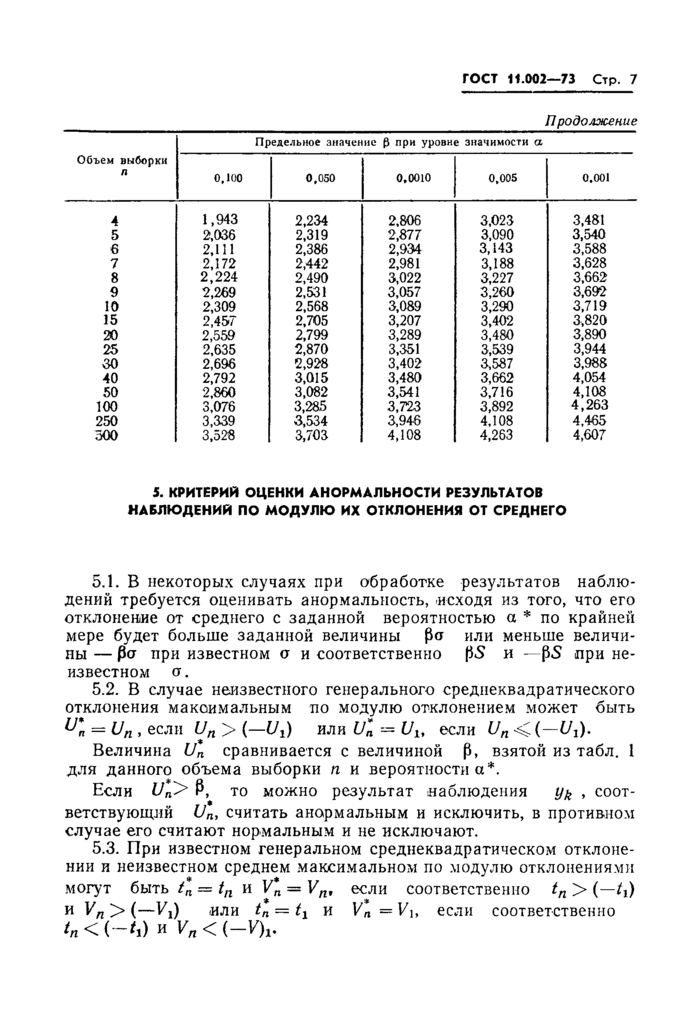
5. КРИТЕРИЙ ОЦЕНКИ АНОРМАЛЬНОСТИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПО МОДУЛЮ ИХ ОТКЛОНЕНИЯ ОТ СРЕДНЕГО | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5.1. В некоторых случаях при обработке результатов наблюдений требуется оценивать анормальность, исходя из того, что его отклонение от среднего с заданной вероятностью а * по крайней мере будет больше заданной величины ра или меньше величины — pa при известном о и соответственно р£ и ^PS при неизвестном а.
5.2. В случае неизвестного генерального среднеквадратического отклонения максимальным по модулю отклонением может быть U*n = Unj если Un > (—иг) или Un = Ut, если Un < (-Ui).
Величина Un сравнивается с величиной Р, взятой из табл. 1 для данного объема выборки п и вероятностна*.
Если U*n> Р, то можно результат наблюдения , соответствующий Un, считать анормальным и исключить, в противном случае его считают нормальным и не исключают.
5.3. При известном генеральном среднеквадратическом отклоне
нии и неизвестном среднем максимальном по модулю отклонениями могут быть tn = tn и V*n = Vn, если соответственно tn > (~/х) и Vп > (—Vj) или tn = tx и Vn=Vu если соответственно
*л <( —*i) и vn <(—V%
Величины С и V*n сравнивают с величинами Р , взятыми соответственно для in из табл. 3 и для Vn из табл. 4 для данного объема выборки п и вероятности а*. Если величина tn или Vn окажется больше р, то соответствующий результат наблюдения уь можно считать анормальным и исключить, в противном случае его считают нормальным и не, исключают.
Таблица 4
|
Предельные значения р для случая известного генерального среднеквадратического отклонения а и известного генерального среднего а а* = Bep^maxj yk g ■■] > р) k~l tn. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5.4. Следует иметь в виду, что а*~2а и поэтому для оценки анормальности результатов наблюдений по модулю отклонения от среднего в табл. 1—2 внизу даны числовые значения для замены а на 2а.
Примеры применения критериев оценки анормальности результатов наблюдений по модулю отклонения от среднего приведены в приложении 1 (примеры 5 и 6).