ГОСТ Р 8.744-2011
Государственная система обеспечения единства измерений. Оптика и фотоника. Интерференционные измерения оптических элементов и систем. Часть 3. Калибровка и аттестация интерферометров, методика измерений оптических волновых фронтов
Купить ГОСТ Р 8.744-2011 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Рассматривает источники погрешностей и деление их на симметричные и несимметричные части. В нем также описываются критерии оценки надежности результатов измерений по качеству физически реализуемой эталонной поверхности и создание методик испытаний, обеспечивающих достижение абсолютной калибровки.
Идентичен ISO/TR 14999-3:2005
Оглавление
1 Область применения
2 Термины и определения
3 Систематическое исследование контрольного оборудования, измерительной установки и окружающей среды как источников погрешностей
3.1 Общие сведения
3.2 Источники неопределенности
3.3 Суммирование неопределенностей
4 Деление погрешностей на составляющие с вращательной симметрией и невращательной симметрией (вращательно-симметричные и невращательно-симметричные)
4.1 Общие сведения
4.2 Принцип
4.3 Измерительная аппаратура
4.4 Методика выполнения измерений
5 Измерение качества физически реализованной эталонной поверхности
5.1 Плоскости
5.2 Сферы
5.3 Асферики
5.4 Контроль однородности
5.5 Оптические системы в режиме пропускания
6 Методики абсолютной калибровки
6.1 Общие сведения
6.2 Плоскости
6.3 Сферические поверхности
6.4 Цилиндрические поверхности
6.5 Прозрачные оптические окна
Библиография
| Дата введения | 01.03.2013 |
|---|---|
| Добавлен в базу | 01.10.2014 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Экология
- Раздел Электроэнергия
Организации:
| 13.12.2011 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 1067-ст |
|---|---|---|---|
| Разработан | ФГУП ВНИИМС | ||
| Издан | Стандартинформ | 2013 г. |
State system for ensuring the uniformity of measurements. Optics and photonics. Interferometric measurement of optical elements and optical systems. Part 3. Calibration and validation of interferometric test equipment and measurements
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11
стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20
стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26

стр. 27

стр. 28

стр. 29

стр. 30
НАЦИОНАЛЬНЫМ
СТАНДАРТ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
ГОСТР8.744-
2011/ISO/TR14999-3:2005Государственная система обеспечения единства измеренийОПТИКА И ФОТОНИКА. ИНТЕРФЕРЕНЦИОННЫЕ ИЗМЕРЕНИЯ ОПТИЧЕСКИХ ЭЛЕМЕНТОВ И СИСТЕМ
14999-3:2005Государственная система обеспечения единства измеренийОПТИКА И ФОТОНИКА. ИНТЕРФЕРЕНЦИОННЫЕ ИЗМЕРЕНИЯ ОПТИЧЕСКИХ ЭЛЕМЕНТОВ И СИСТЕМ
ОПТИКА И ФОТОНИКА. ИНТЕРФЕРЕНЦИОННЫЕ ИЗМЕРЕНИЯ ОПТИЧЕСКИХ ЭЛЕМЕНТОВ И СИСТЕМ
Часть 3
Калибровка и аттестация интерферометров, методика измерений оптических волновых фронтов
ISO/TR 14999-3:2005 Optics and photonics — Interferometric measurement of optical elements and optical systems. Part 3: Calibration and validation of interferometric test equipment and measurements (IDT)
Издание официальное
Москва
Стандартинформ
2013
ГОСТ Р 8.744-2011/ISO/TR 14999-3:2005Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации — ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологической службы» (ФГУП «ВНИИМС»)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 53 «Основные нормы и правила по обеспечению единства измерений» Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 13 декабря 2011 г. № 1067-ст
4 Настоящий стандарт идентичен международному документу ISO/TR 14999-3:2005 «Оптика и фотоника. Интерферометрическое измерение оптических элементов и систем. Часть 3. Калибровка и валидация оборудования для интерферометрического испытания и измерений» (ISCVTR 14999-3:2005 «Optics and photonics — Interferometric measurement of optical elements and optical systems. Part 3: Calibration and validation of interferometric test equipment and measurements»)
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячно издаваемом информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
© Стандартинформ, 2013
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
ГОСТ Р 8.744-2011/ISO/TR 14999-3:2005
Пример — В 6.2 описан метод «трех плоскостей», когда плоская поверхность N1 сравнивается с плоской поверхностью N2, затем с N3, а N3, в свою очередь, с N2, в результате чего пользователь получает отклонения всех трех плоских поверхностей от идеальной формы.
Эталон и образец можно рассматривать отдельно путем введения непрозрачного экрана в плечи интерферометра. Перемещать можно как эталон, так и образец. Направление и величина перемещения выбираются пользователем, который может при желании исключить одну или более трансляций. Интерференционные картины формируются путем алгебраического суммирования дефектов эталона и образца, причем предоставляют информацию об обеих поверхностях.
Эталон и образец можно рассматривать отдельно путем введения непрозрачного экрана в плечи интерферометра. Вращать можно как эталон, так и образец. Углы поворота выбираются пользователем, который может при желании исключить одно или более вращений. Интерференционные картины формируются путем алгебраического суммирования дефектов эталона и образца, причем предоставляют информацию об обеих поверхностях.
5.1.3 Калибровочный сертификат
Выпускаемые промышленностью интерферометры и вспомогательные (в отечественной трактовке разрядные) эталонные плоские поверхности должны снабжаться калибровочными сертификатами. Калибровочный сертификат на эталонную плоскую поверхность должен содержать информацию о ее неплоскостности, а также детальное отображение расположения и размеры дефектов.
5.2 Сферы5.2.1 Общие сведения
Оптическое качество вогнутого или выпуклого волновых фронтов может быть определено по отношению к физически реализованной сферической поверхности, откалиброванной по задаваемым параметрам, т. е. с известным оптическим качеством. При этом следует иметь в виду когерентность излучения источника. Как сферический волновой фронт, так и сферическая эталонная поверхность имеют центры кривизны.
Для получения требуемой интерференционной картины оба центра кривизны следует расположить как можно ближе друг к другу. Пользователь может добиться этого юстировкой плеч интерферометра.
5.2.2 Настройка интерферометра по идеальному эталону
Каждая разъюстировка центров кривизны приводит к интерференционной картине, свидетельствующей о появлении разности хода между сферическими волновыми фронтами.
При юстировке интерферометра могут формироваться следующие интерференционные картины:
- оба центра кривизны расположены один за другим на оптической оси: интерферограмма представляет собой совокупность концентрических колец;
- оба центра кривизны лежат в одной плоскости, перпендикулярной оптической оси: результат — интерференционная картина Юнга, т. е. совокупность прямолинейных полос;
- один из центров кривизны расположен не на оптической оси и не в той же плоскости, что и второй центр: интерференционная картина в виде эллипсов или парабол.
При настройке интерферометра следует добиваться картины в виде концентрических полос, учитывая, что:
- расстояние между кольцами возрастает, когда оба центра кривизны приближаются друг к другу;
- полоса нулевого порядка имеет место при совмещении центров кривизны;
- оставшиеся после юстировки интерференционные полосы соответствует дефектам контролируемого образца.
5.2.3 Оценка качества эталона
Метод «трех сфер» позволяет определить качество сферического эталона так же, как метод «трех плоскостей» позволяет сделать то же самое применительно к плоскому эталону (см. также 6.3).
Оптическое производство позволяет изготовить сопряженные пары вогнутых и выпуклых сферических эталонов одинакового радиуса путем их совместной полировки. Процедура оценки их качества та же, что и для плоских эталонов.
5.2.4 Альтернативный метод
Этот метод применим к сферам с радиусом, превышающим несколько метров. В этом случае эталоном может служить плоское зеркало, тогда интерференционная картина после правильной юстировки будет представлять собой совокупность концентрических колец. Пользователь может контролировать правильность определения кривизны поверхности, следя за расстоянием между полосами (кольцами).
7
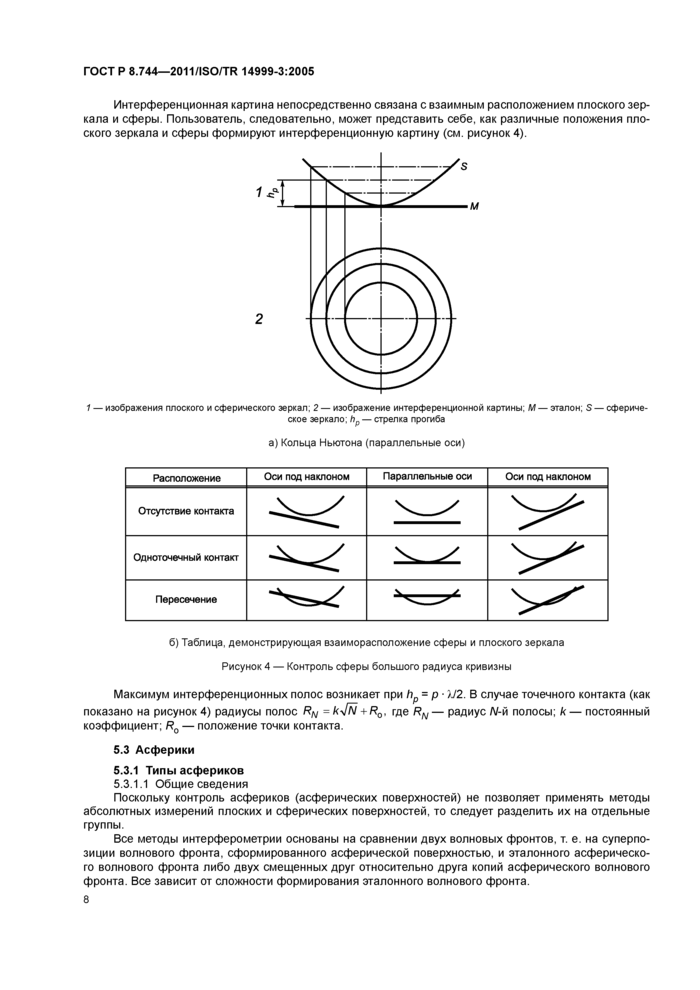
Интерференционная картина непосредственно связана с взаимным расположением плоского зеркала и сферы. Пользователь, следовательно, может представить себе, как различные положения плоского зеркала и сферы формируют интерференционную картину (см. рисунок 4).
|
1 — изображения плоского и сферического зеркал; 2 — изображение интерференционной картины; М — эталон; S — сферическое зеркало; hp — стрелка прогиба |
|
а) Кольца Ньютона (параллельные оси) | ||||||||||||||||
| ||||||||||||||||
|
б) Таблица, демонстрирующая взаиморасположение сферы и плоского зеркала Рисунок 4 — Контроль сферы большого радиуса кривизны |
Максимум интерференционных полос возникает при hp = р • XJ2. В случае точечного контакта (как показано на рисунок 4) радиусы полос R^ = k^N +R0, где RN — радиус N-й полосы; к — постоянный коэффициент; R0 — положение точки контакта.
5.3 Асферики5.3.1 Типы асфериков
5.3.1.1 Общие сведения
Поскольку контроль асфериков (асферических поверхностей) не позволяет применять методы абсолютных измерений плоских и сферических поверхностей, то следует разделить их на отдельные группы.
Все методы интерферометрии основаны на сравнении двух волновых фронтов, т. е. на суперпозиции волнового фронта, сформированного асферической поверхностью, и эталонного асферического волнового фронта либо двух смещенных друг относительно друга копий асферического волнового фронта. Все зависит от сложности формирования эталонного волнового фронта.
ГОСТ Р 8.744-2011/ISO/TR 14999-3:2005
В обычной интерферометрии имеют дело с плоским или сферическим волновыми фронтами по двум причинам: во-первых, они легко трансформируются один в другой с помощью дифракционноограниченной оптики; во-вторых, калибровка осуществляется методами абсолютных измерений на основе сочетания методов относительных измерений, т. е. когда контролируемый объект размещается в различных положениях. Плоский и сферический волновые фронты и простые оптические элементы типа плоских и сферических поверхностей играют ключевую роль, так как их можно похожим способом использовать при калибровке.
Следующим важнейшим моментом является необходимость применения методов интерферометрии с формированием интерферограмм в области низких пространственных частот, по крайней мере, по двум причинам. Первая из них связана с теоремой Найквиста—Котельникова, а вторая — с возникновением неизбежных больших погрешностей, если в интерферограмме имеют место значительные отклонения.
Если градиент отклонений увеличивается или возрастает разность фаз между волновыми фронтами (опорным и контролируемым), то все погрешности и неточности юстировки в интерферограмме приводят к большим погрешностям измерений.
Поэтому асферики целесообразно разделить на три группы соответственно возрастанию сложности и полноты эксперимента: стигматические; плавные и крутые асферики.
5.3.1.2 Стигматические асферики
Стигматическими именуются асферики, преобразующие сферический волновой фронт в другой волновой фронт с иным радиусом кривизны. Это же относится к преобразованию плоского волнового фронта в сферический.
Стигматические асферики (например, конические поверхности, параболоиды, эллипсоиды, гиперболоиды) обычно контролируются в интерферометрах типа Тваймана—Грина или им подобных, поскольку имеет место преобразование сферических волновых фронтов в сферические, плоских волновых фронтов в сферические и наоборот, сферических волновых фронтов в плоские. В подавляющем большинстве случаев представляется возможность объединения нескольких широкоапертурных оптических элементов, обеспечивающего сравнение порожденного асфериком волнового фронта с плоским или простым сферическим волновым фронтом [5].
В большинстве интерферометров предпочтительно использовать плоские волновые фронты, иначе светоделитель пучков может внести значительные погрешности в результаты измерений.
5.3.1.3 Плавные асферики
Плавными именуются асферические поверхности, слегка отличающиеся от плоских или сферических поверхностей с соответствующими радиусами кривизны. Следовательно, их контроль можно проводить на интерферометре Физо с осветителем, оптическая система которого формирует волновой фронт с заданной кривизной эталонной поверхности.
5.3.1.4 Крутые асферики
В данном случае для формирования эталонного асферического волнового фронта требуется достаточно сложная аппаратура и высокая квалификация экспериментатора. Необходимы такие компенсирующие оптические элементы и системы, как, например, «нулевая оптика», составленная из простых линз, или даже целые оптические системы для сопряжения идеального асферического волнового фронта. В большинстве случаев предполагается использование синтезированных голограмм или дифракционных оптических элементов, которые формируют как эталонную асферическую волну, так и сопряженную ей.
5.3.2 Методики контроля
5.3.2.1 Методики контроля стигматических асфериков
Как упоминалось ранее, контроль проводится на интерферометрах типа Тваймана—Грина, однако для гарантированного формирования плоской волны на входе и выходе интерферометра используются вспомогательные оптические элементы (системы). Для получения общего представления об этих методиках контроля приводятся два примера.
На рисунках 5 и 6 приведены оптические схемы контроля соответственно параболоидов и эллипсоидальных зеркал.
9
ГОСТ Р 8.744-2011/ISO/TR 14999-3:2005
|
1 — плоское зеркало; 2 — параболоид; 3 — формирующая оптическая система; 4 — поляризационный светоделитель; а — излучение лазера; 6 — излучение, направленное к приемнику Рисунок 5 — Контроль параболоида |
|
б б |
|
1 — формирующая оптическая система; 2 — эллипсоид; 3 — плоское опорное зеркало; 4 — светоделитель; Ff — точка фокусировки отраженной волны; F2 — точка фокусировки падающей волны; а — излучение лазера; б — излучение, направленное к приемнику Рисунок 6 — Контроль эллипсоидального зеркала |
5.3.2.2 Контроль с использованием интерферометра Физо (метод пробного стекла)
Плавные асферики можно контролировать путем сравнения асферической поверхности со сферической согласованной кривизны, или, в некоторых случаях, с плоскими пробными стеклами. Согласование означает, что интерферометр Физо создает низкочастотную интерферограмму Максимум возможного расхождения асферической поверхности с согласующей сферой определяется теоремой Найквиста и ограничениями, накладываемыми допустимой систематической погрешностью.
Для определения наиболее подходящего волнового фронта источника излучения необходим тщательный анализ возможных систематических погрешностей. Первый вариант заключается в выборе этого волнового фронта, согласованного с опорной поверхностью. На рисунке 7 приведен типичный пример плавного выпуклого асферика. В первом приближении применение этой методики обеспечивает расхождения с наиболее подходящей по форме сферой порядка нескольких микрометров.
ю
ГОСТ Р 8.744-2011/ISO/TR 14999-3:2005
1 — формирующая оптика; 2 — сферическая опорная поверхность; 3 — асферическая поверхность; а — излучение лазера; б— излучение, направленное к
приемнику
Рисунок 7 — Оптическая схема интерферометра Физо с выпуклой асферической поверхностью и со вспомогательным пробным стеклом
5.3.2.3 Методика интерферометрии сдвига
|
а а |
Поскольку могут существовать значительные расхождения между асферическим волновым фронтом и простейшими плоским или сферическим волновыми фронтами, целесообразно применять оптические схемы интерферометров с небольшим количеством полос. Наибольшее распространение получила интерферометрия сдвига, когда волновая поверхность, порожденная асфериком, сравнивается со своим дубликатом, который, в свою очередь, может быть сформирован разными путями. Это может быть смещенный, повернутый или перевернутый дубликат. Для получения наиболее полной информации необходимо в некоторых случаях производить измерения в двух ортогональных направлениях сдвига. Типичным примером может служить интерферометр Майкельсона, в котором асферическая волна фокусируется на расположенных под наклоном зеркалах, обеспечивающих поперечный сдвиг двух волновых фронтов (рисунок 8).
1 — асферический волновой фронт;
2 — светоделитель; М1 — первое зеркало; М2 — второе зеркало; а — излучение, направленное к приемнику
Рисунок 8 — Интерферометр сдвига на основе интерферометра Майкельсона—Найквиста и ограничениями, накладываемыми допустимой систематической погрешностью
11
Альтернативный вариант — дифракционная решетка Рончи и другие портативные двухпучевые интерферометры, неоднократно описанные в литературе [5].
Для плавных асферических волновых фронтов перспективно применение оптических схем интерферометров радиального сдвига, когда исходный волновой фронт сопоставляется с асферическим волновым фронтом, увеличенным в поперечном направлении по масштабу (рисунок 9). При этом радиальный сдвиг может быть сделан сколь угодно большим, таким, что в первом приближении интерферограммы непосредственно отражают практически в реальном масштабе имеющие место отклонения волнового фронта.
|
Рисунок 9 — Циклический интерферометр радиального сдвига |
5.3.2.4 Нулевые методы контроля с использованием преломляющих оптических систем и компьютерных синтезированных голограмм
Во избежание возникновения систематических погрешностей и использования сложных вычислительных процедур стараются применять схемы интерферометров, в которых светоделители минимально искажают волновые фронты. Это может быть достигнуто путем использования компенсационных оптических элементов, формирующих волновой фронт, сопряженный с волновым фронтом, преломленным или отраженным асферической линзой или асферическим зеркалом. Если идеальный асфе-
рик формирует волновой фронт с комплексной амплитудой е,кУ[,а^х’у\ то компенсирующая оптическая
система (нулевая линза) должна воспроизводить сопряженный волновой фронт e~ikWa^x,y^ таким образом, чтобы в последующей серии экспериментов воспроизводился практически плоский (за исключением неизбежных отклонений реального волнового фронта от идеального) волновой фронт, интерферирующий с плоской опорной волной.
На первый взгляд эта концепция представляется противоречивой, поскольку формирование сопряженного асферического волнового фронта e~ikWa(-x'y^ требует в общем случае использования сложных оптических систем, которые сами по себе не могут быть проконтролированы с достаточной точностью, поскольку формируют такой же асферический фронт с его деформациями, но противоположного знака. Однако при наличии нулевого объектива, содержащего несколько (или даже один) оптических элементов, у которых достаточно точно измерена сферичность, проблема нулевого объектива может быть решена.
ГОСТ Р 8.744-2011/ISO/TR 14999-3:2005
Однако наиболее предпочтительным вариантом является использование дифракционных оптических элементов или компьютерных синтезированных голограмм. С помощью последних можно воспроизвести любые волновые аберрации. Хорошо известно [6], что компьютерная голограмма формирует, по крайней мере, два порядка дифракции с сопряженными по фазе комплексными амплитудами. Поэтому очевидно, что освещение такой компьютерной голограммы плоской опорной волной приведет к формированию, по крайней мере, двух первых дифракционных порядков, которые затем успешно могут быть разделены пространственными фильтрами.
Возможны три варианта введения компьютерных голограмм в интерферометры:
а) компьютерная голограмма вводится в то плечо интерферометра, в котором сформирован плоско-параллельный пучок излучения, и она непосредственно замещает реальный эталон;
б) компьютерная голограмма используется для компенсации асферичности волнового фронта и формирования плоского, сферического или другого известного опорного волнового фронта; следовательно, она вводится в то же плечо, что и асферическая поверхность, и замещает нулевой объектив (линзу);
в) компьютерная голограмма вводится после интерферометра и несет информацию об асферической поверхности в виде муаровой картины.
Использование асимметричных фазовых рельефов позволяет получить компьютерные голограммы лишь с одним дифракционным порядком. Эти голограммы были применены при испытаниях ас-фериков [7—9], а также в качестве киноформов (синтезированных голограмм) в случае вращательной симметрии [10].
Во избежание искривления волнового фронта необходимо обеспечить минимальное расстояние между нулевым объективом (линзой) или компьютерной голограммой и асфериком, что, помимо всего, облегчит вычисления и упростит производство оптических элементов. Эффект искривления волнового фронта хорошо известен применительно к крутым асферикам, не обладающим стигматическими свойствами. Крутые асферики являются частями оптических систем, в которых они служат компенсаторами волновых фронтов. Типичным представителем такого компенсатора служит пластина Шмидта.
Наиболее совершенная компьютерная голограмма — нулевая линза, обеспечивает падение плоского волнового фронта на расположенные друг за другом компьютерную голограмму и асферик. На рисунке 10 представлена оптическая схема для проходящего света, а на рисунке 11 —для отраженного света с применением пропускающей компьютерной голограммы. Отрицательная линза, компьютерная голограмма и асферическое зеркало последовательно введены в одно плечо интерферометра Май-кельсона. Компьютерная голограмма из падающей сферической волны формирует волну, падающую на асферическое зеркало перпендикулярно к его поверхности во всех точках. После отражения и последующей дифракции на компьютерной голограмме формируется почти сферическая волна, отражающая отклонения асферической поверхности.
|
3 1 1 — асферическая линза; 2 — поляризационный светоделитель; 3 — компьютерная голограмма Рисунок 10 — Компьютерная голограмма в качестве нулевой линзы при контроле асферической линзы в проходящем свете |
13
|
1 — лазер; 2 — опорное зеркало; 3 — светоделитель; 4 — отрицательная линза; 5 — пространственный фильтр; 6 — асферическая поверхность; 7 — плоскость интерференции; 8 — формирователь изображения; 9 — компьютерная голограмма Рисунок 11 — Компьютерная голограмма в роли компенсатора при контроле асферической поверхности |
Преимущества обеих оптических схем заключены в том, что оптические элементы интерферометра пропускают почти плоские волновые фронты, тем самым минимизируются систематические погрешности. В случае строгой симметрии интерферометра другой сопряженный волновой фронт может быть использован путем размещения компьютерной голограммы в опорном плече (рисунок 12). Вспомогательная линза формирует волновой фронт со сферической кривизной. Компьютерная голограмма лишь создает отклонения от асферичности.
|
1 — лазер; 2 — конденсор; 3 — вспомогательная линза; 4 — светоделитель; 5 — асферическая поверхность; б — плоскость интерференции; 7 — диафрагма; 8 — формирователь изображения; 9 — компьютерная голограмма Рисунок 12 — Интерферометр Майкельсона со вспомогательной линзой и компьютерной голограммой |
В случаях, когда отклонения асферической поверхности незначительны и систематические погрешности остаются в допустимых пределах, компьютерная голограмма может быть помещена вне интерферометра. Результирующая интерферограмма может быть интерпретирована как муаровые полосы между компьютерной голограммой и интерференционной картиной в ее плоскости. При исполь-
ГОСТ Р 8.744-2011/ISO/TR 14999-3:2005
зовании пространственной фильтрации суперпозиция дифрагировавшей опорной волны и предметной волны нулевого порядка демонстрирует отклонения асферики от идеальной поверхности (рисунок 13). Компьютерная голограмма освещается плоской волной и формирует в первом порядке дифракции опорную волну для получения волны, отраженной испытуемым асферическим зеркалом. Пространственный фильтр предназначен для разделения дифрагировавшего света от недифрагировавшего.
Вращательно-симметричные асферики могут быть испытаны с использованием осесимметричных компьютерных голограмм. Поскольку все дифракционные порядки расположены на оси, в центре интерферограммы наблюдаются лишь незначительные искажения. В случаях, когда искажения асферической поверхности слишком малы и пространственное разделение дифракционных порядков становится затруднительным, то для получения дефокусировки можно добавить некоторую квадратичную фазовую функцию. Такая осесимметричная компьютерная голограмма может быть низкочастотной, что значительно упрощает процесс ее изготовления (рисунок 14). Падающая плоская волна преобразуется на параболическом зеркале в сферическую волну, дифрагирующую на осесимметричной голограмме и интерферирующую с плоской опорной волной, которая отражается в том же направлении опорным
|
1 — лазер; 2 — опорная волна; 3 — отрицательная линза; 4 — испытуемое зеркало; 5 — плоскость интерференции; 6 — пространственный фильтр; 7 — формирователь изображения; 8 — компьютерная голограмма Рисунок 13 — Включение интерферометра последовательно с компьютерной голограммой — источником несущей частоты |
зеркалом.
2 3
1 — лазер; 2 — опорное зеркало; 3 — светоделитель; 4 — параболическое зеркало; 5 — плоскость интерференции; 6 — пространственный фильтр; 7 — формирователь изображения; 8 — осесимметричная голограмма
Рисунок 14 — Осесимметричная голограмма для испытаний асферических зеркал
5.3.2.5 Относительный контроль асфериков
Как хорошо известно, в голографии волновой фронт может быть зафиксирован на фотопластинке при выполнении определенных условий ограничения пространственных частот [11]. При контроле гладких поверхностей эти условия, как правило, выполняются. Однако при изменениях состояния объекта (например, в процессе полировки оптического элемента) зарегистрированное на голограмме изображение может оказаться непригодным для последующего сравнения с новым изображением поверхности объекта. Возможность такого сравнения предоставляет голография в реальном масштабе времени, когда сравниваются два состояния объекта в моменты времени т1 и т2. При высоких требованиях к точности и сходимости результатов измерений применение голографической методики становится проблематичным, если несущая частота на голограмме слишком высока. В этом случае поперечное «сжатие» фотослоя становится особенно заметным. Более того, голографические пластины, как правило, недостаточно стабильны, что, в свою очередь, порождает искажения волнового фронта.
|
1 — источник белого света; 2 — голограмма I; 3 — асферическая поверхность А; 4 — светоделитель; 5 — асферическая поверхность В (или С); б — селектор первого порядка дифракции; 7 — голограмма II; 8 — формирователь изображения; а — излучение лазера Рисунок 15 — Интерферометр с двумя компенсирующими голограммами для контроля асферических поверхностей |
В некоторых случаях полезно уменьшить несущую частоту путем сближения формы опорной волны с формой поверхности (волновым фронтом) объекта. Подобный способ описан применительно к сферам в работе [12]. Он также применим и для асферических поверхностей. Для его реализации две асферические поверхности идентичной формы помещаются в интерферометр Тваймана—Грина (рисунок 15). При надлежащей «подгонке» форм асферических поверхностей А и В (или С) голограмма II с низкой несущей частотой может быть использована для регистрации отклонений поверхности В от А. Поскольку интерферометр сам по себе несовершенен, необходимо применение разностного метода сравнения форм асферических поверхностей В и С для компенсации погрешностей самого интерферометра. Так как поверхность А используется в качестве опорной, то ее отклонения при сравнении В и С также исключаются. Для обнаружения расхождений между отклонениями поверхностей В и С используется процедура сравнения муаровой картины, одним объектом которой служит голограмма II с зафиксированными на ней отклонениями между А и В, а другим — интерференционная картина, отображающая разницу между А и С. При этом контраст оказывается весьма слабым. Для его увеличения необходимо перекрыть волну первого порядка дифракции.
1
Однако при наличии сильных деформаций асферических поверхностей пространственное разделение нулевого и первого порядков дифракции оказывается невозможным, так как несущая частота мала (например, 10 линий/мм) и границы спектра пространственных частот простираются дальше, чем промежуток между упомянутыми порядками дифракции. Для сжатия пространственного спектра ча-
ГОСТ Р 8.744-2011/ISO/TR 14999-3:2005Содержание
1 Область применения..................................................................1
2 Термины и определения...............................................................1
3 Систематическое исследование контрольного оборудования, измерительной установки
и окружающей среды как источников погрешностей........................................1
3.1 Общие сведения..................................................................1
3.2 Источники неопределенности.......................................................2
3.3 Суммирование неопределенностей..................................................2
4 Деление погрешностей на составляющие с вращательной симметрией и невращательной
симметрией (вращательно-симметричные и невращательно-симметричные)...................3
4.1 Общие сведения..................................................................3
4.2 Принцип.........................................................................3
4.3 Измерительная аппаратура.........................................................4
4.4 Методика выполнения измерений....................................................5
5 Измерение качества физически реализованной эталонной поверхности.......................5
5.1 Плоскости.......................................................................5
5.2 Сферы..........................................................................7
5.3 Асферики........................................................................8
5.4 Контроль однородности...........................................................18
5.5 Оптические системы в режиме пропускания..........................................18
6 Методики абсолютной калибровки......................................................20
6.1 Общие сведения.................................................................20
6.2 Плоскости......................................................................21
6.3 Сферические поверхности.........................................................26
6.4 Цилиндрические поверхности......................................................29
6.5 Прозрачные оптические окна.......................................................31
Библиография........................................................................32
ГОСТ Р 8.744-2011/ISO/TR 14999-3:2005
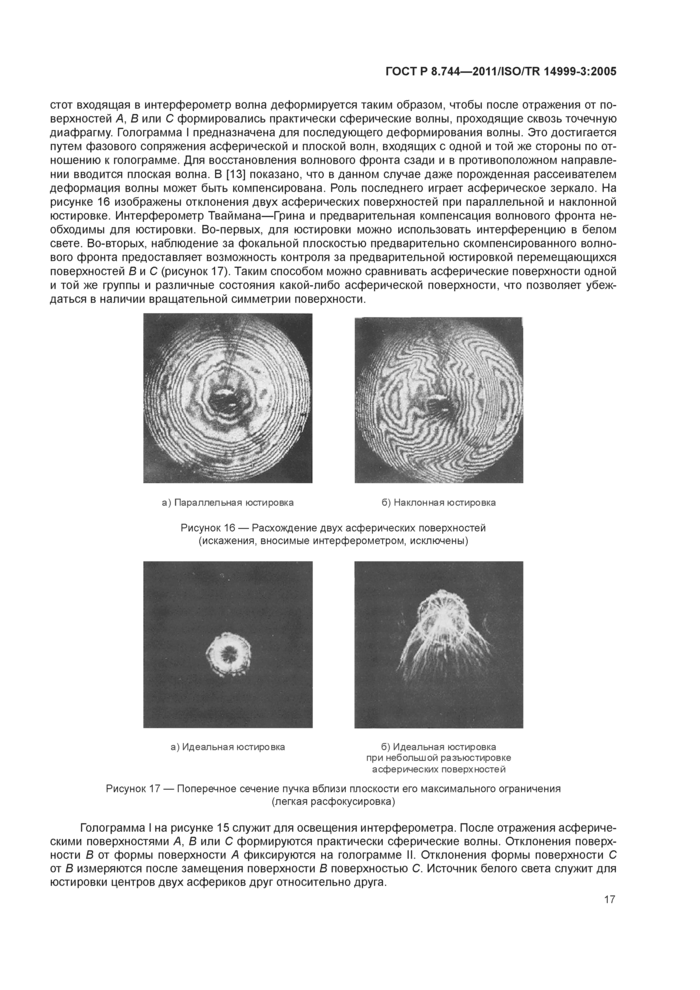
а) Параллельная юстировка
б) Наклонная юстировка
Рисунок 16 — Расхождение двух асферических поверхностей (искажения, вносимые интерферометром, исключены)
а) Идеальная юстировка б) Идеальная юстировка
при небольшой разъюстировке асферических поверхностей
|
а) Параллельная юстировка |
|
б) Наклонная юстировка |
|
Рисунок 16 — Расхождение двух асферических поверхностей (искажения, вносимые интерферометром, исключены) |
|
а) Идеальная юстировка б) Идеальная юстировка при небольшой разъюстировке асферических поверхностей |
стот входящая в интерферометр волна деформируется таким образом, чтобы после отражения от поверхностей А, В или С формировались практически сферические волны, проходящие сквозь точечную диафрагму. Голограмма I предназначена для последующего деформирования волны. Это достигается путем фазового сопряжения асферической и плоской волн, входящих с одной и той же стороны по отношению к голограмме. Для восстановления волнового фронта сзади и в противоположном направлении вводится плоская волна. В [13] показано, что в данном случае даже порожденная рассеивателем деформация волны может быть компенсирована. Роль последнего играет асферическое зеркало. На рисунке 16 изображены отклонения двух асферических поверхностей при параллельной и наклонной юстировке. Интерферометр Тваймана—Грина и предварительная компенсация волнового фронта необходимы для юстировки. Во-первых, для юстировки можно использовать интерференцию в белом свете. Во-вторых, наблюдение за фокальной плоскостью предварительно скомпенсированного волнового фронта предоставляет возможность контроля за предварительной юстировкой перемещающихся поверхностей В и С (рисунок 17). Таким способом можно сравнивать асферические поверхности одной и той же группы и различные состояния какой-либо асферической поверхности, что позволяет убеждаться в наличии вращательной симметрии поверхности.
Рисунок 17 — Поперечное сечение пучка вблизи плоскости его максимального ограничения
(легкая расфокусировка)
Голограмма I на рисунке 15 служит для освещения интерферометра. После отражения асферическими поверхностями А, В или С формируются практически сферические волны. Отклонения поверхности В от формы поверхности А фиксируются на голограмме II. Отклонения формы поверхности С от В измеряются после замещения поверхности В поверхностью С. Источник белого света служит для юстировки центров двух асфериков друг относительно друга.
Введение
Техническим комитетом ИСО (1БОЯС 172/SC1) была подготовлена и опубликована под общим названием ИСО 10110 «Оптика и фотоника — Подготовка технической документации на оптические элементы и системы» серия международных стандартов «Обозначения в технической документации характеристик оптических элементов и систем», причем особое внимание уделено части 5 «Допустимые отклонения формы поверхности» и части 14 «Допустимые отклонения волнового фронта».
После опубликования серии стандартов и особенно упомянутых двух частей экспертам стало очевидно, что необходимы дополнительная документация и информация о представлении изготовленных оптических элементов и систем с допустимыми отклонениями. Поэтому ISO/ТС 172/SC1 подготовил и опубликовал Технический доклад под названием «Интерферометрия волновых фронтов и форм поверхностей оптических элементов».
При обсуждении было констатировано, что Технический доклад или стандарт впервые имеют отношение к волновой оптике, т. е. базируются на физической оптике, а не геометрической. Поэтому пояснены только основные аспекты, представляющие наибольшие трудности для понимания.
С учетом складывавшейся ситуации, когда в документах ИСО не обсуждались проблемы интерферометрии, естественным было желание сделать изложение предельно доступным. Возникла дискуссия по вопросу о целесообразности обсуждения таких важнейших направлений, как интерференционная микроскопия (для наблюдения и описания микрошероховатостей поверхностей оптических элементов), интерферометрия сдвига (например, для описания подвергшихся коррекции оптических систем), многолучевая интерферометрия, формирование и считывание изображений в когерентном излучении или методы обращения волнового фронта. Решено было отразить и такие методы, как классическая двулучевая интерферометрия, а также с распространенными методиками типа голографической интерферометрии, муаровым методом и профилометрией, наряду с Фурье-спектроскопией и поляриметрией, которые дополняют микроскопическую интерферометрию (микроинтерферометрию).
Для дополнения ИСО 10110 изложение материала содержало описание общепринятых способов оценки качества оптических элементов. Это было выполнено путем укомплектования первой версии Технического доклада несколькими дополнительными частями с учетом того, что в ближайшем будущем возникнут более жесткие допуски на отклонения от идеальной формы или шероховатости поверхности (примерно на два порядка) оптических элементов и систем, предназначенных для работы в экстремальном вакуумном ультрафиолете (I = 6—13 нм) в системах микролитографии.
Данный стандарт (ИСО 14999) посвящен методам оценки качества оптических элементов и систем в целом, имеющих отношение к производимым ими (элементами и системами) деформациям волнового фронта. Эти искажения распределены по шкале пространственных частот, однако в данном стандарте (ИСО 14999) рассматриваются деформации волнового фронта только в низко- и среднечастотном диапазонах спектра пространственных частот. Высокочастотный участок спектра может быть измерен только с помощью микроскопа, с использованием результатов измерений рассеянного света или вообще неоптических способов зондирования поверхности.
Подобное рассмотрение может быть выполнено применительно к любому спектральному диапазону излучения, используемого для зондирования поверхности. В ИСО 14999 для наглядности рассмотрен случай использования видимого излучения. В ряде случаев при измерениях шероховатости поверхности применяются С02-лазеры с длиной волны 10,6 мкм (после шлифования изделия) или эксимерные лазеры с длинами волн 193 или 248 нм при контроле микролитографической оптики. Однако в стандарте они упоминаются изредка и не детализируются. Об остальных участках оптического спектра речь в ИСО 14999 не идет.
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИГосударственная система обеспечения единства измеренийОПТИКА И ФОТОНИКА.ИНТЕРФЕРЕНЦИОННЫЕ ИЗМЕРЕНИЯ ОПТИЧЕСКИХ ЭЛЕМЕНТОВ И СИСТЕМЧасть 3Калибровка и аттестация интерферометров, методика измерений оптических волновых фронтов
ОПТИКА И ФОТОНИКА.ИНТЕРФЕРЕНЦИОННЫЕ ИЗМЕРЕНИЯ ОПТИЧЕСКИХ ЭЛЕМЕНТОВ И СИСТЕМЧасть 3Калибровка и аттестация интерферометров, методика измерений оптических волновых фронтов
Часть 3Калибровка и аттестация интерферометров, методика измерений оптических волновых фронтов
State system for ensuring the uniformity of measurements. Optics and photonics. Interferometric measurement of optical elements and systems. Part 3. Calibration and validation of interferometers, methodology of optical uavefronts
measurement
Дата введения — 2013—03—01
1 Область применения
Настоящий стандарт рассматривает источники погрешностей и деление их на симметричные и несимметричные части. В нем также описываются критерии оценки надежности результатов измерений по качеству физически реализуемой эталонной поверхности и создание методик испытаний, обеспечивающих достижение абсолютной калибровки.
2 Термины и определения
В настоящем стандарте применены следующие термины и определения:
2.1 идеальная форма: Математическое описание формы оптической поверхности.
2.2 погрешность поверхности: Отклонение контролируемой поверхности от идеальной формы, включая воздействия, оказываемые силой тяжести и креплением.
2.3 погрешность волнового фронта: Отклонение формы волнового фронта, соответствующее отклонению поверхности, определяемое по интерферограмме.
2.4 абсолютное измерение: Методика, выявляющая отклонение волнового фронта контролируемого объекта относительно идеальной формы, а не физически реализованной поверхности.
2.5 квазиабсолютное измерение: Методика, выявляющая отклонение формы волнового фронта, ограниченное определенными источниками, но также относительно идеальной формы, а не физически реализованной поверхности.
3 Систематическое исследование контрольного оборудования, измерительной установки и окружающей среды как источников погрешностей3.1 Общие сведения
Как известно, целью измерения является определение значения измеряемой величины, причем в контексте данного стандарта эта оптическая величина или параметр, как, например, форма волнового фронта, связана с характеристиками оптических элементов или оптических систем. Измерение начинается с выбора подходящей измеряемой величины, определения метода и соответствующей методики выполнения измерений.
Издание официальное
Любой результат измерения в силу несовершенства самого процесса измерения отягощен погрешностью измерений. Вследствие неопределенности измерений истинное значение измеряемой величины всегда неизвестно.
Неопределенность измерения содержит много составляющих. Некоторые из них определяются статистическими методами и характеризуются экспериментально получаемыми стандартными отклонениями (часто именуемыми стандартными неопределенностями). Другие составляющие неопределенности определяются экспериментальным путем или с использованием других источников информации и вычисляются исходя из предполагаемых распределений вероятности. Они также характеризуются стандартными отклонениями.
Случайные погрешности выявляются в ходе выполнения повторных измерений в одних и тех же условиях измерений. Это приводит к рассеянию результатов вокруг среднего значения. Они не могут быть исключены, но порождаемая ими неопределенность измерений может быть уменьшена путем увеличения числа измерений и статистической обработки получаемых результатов.
Систематические погрешности порождаются систематическими воздействиями. Они остаются практически неизменными при повторных измерениях, выполняемых в тех же условиях. Их нельзя исключить, но можно скорректировать до определенного уровня (т. е. до уровня неисключенной систематической погрешности, получившей общее признание в отечественной метрологии).
Суммарная неопределенность является комбинацией стандартных неопределенностей. Все составляющие неопределенности требуют тщательного изучения и учета, после чего возможна оценка суммарной неопределенности. При предварительной оценке выявляются составляющие, меньшие одной пятой наибольшей компоненты, и ими пренебрегают при оценке суммарной неопределенности. Неопределенности, порождаемые случайными процессами, относятся к неопределенностям типа А, а порождаемые систематически действующими источниками — к неопределенностям типа В.
3.2 Источники неопределенности
Существует много источников неопределенности, которые зависят от технических средств. Однако можно отметить много общих измерительных задач, решение которых связано с оптическими методиками контроля и калибровки:
- недостаточно полное определение типа контроля; предъявляемые требования сформулированы недостаточно точно и детально;
- несовершенство реализации методики контроля; даже при четко определенных условиях проведения контроля не представляется возможным из-за несовершенства системы соблюсти в точности все теоретически определенные соотношения;
- неточности отсчета персоналом показаний аналоговых приборов;
- недостаток разрешающей способности и наличие пороговых соотношений, погрешностей;
- величины, характеризующие эталоны и референтные фантомы;
- изменения характеристик или конструкции средств измерений или референтных фантомов со времени последней калибровки;
- аппроксимация результатов измерений и модернизация метода и методики выполнения измерений;
- случайные помехи в процессе выполнения измерений.
Во-первых, влияния источников неопределенностей могут быть коррелированы; во-вторых, источники систематических погрешностей в ряде случаев могут оказаться незамеченными. Поэтому целесообразно периодически проводить как межпабораторные сличения соответствующих средств измерений, так и перекрестные сличения результатов измерений.
Примечание — Обязательному учету подлежат идентифицированные источники погрешностей при выполнении интерферометрического эксперимента при испытаниях оптических элементов и приборов.
3.3 Суммирование неопределенностей
Наиболее корректными считаются способы учета и суммирования неопределенностей, рекомендуемые GUM [21]. При этом сначала определяются стандартные неопределенности (стандартные отклонения), затем определяется корень квадратный из суммы квадратов стандартных неопределенностей, называемый суммарной стандартной неопределенностью, после чего умножением последней на коэффициент охвата находят расширенную неопределенность. Выбор коэффициента охвата к зависит от уровня доверительной вероятности. При доверительной вероятности « 95 % к = 2.
ГОСТ Р 8.744-2011/ISO/TR 14999-3:20054 Деление погрешностей на составляющие с вращательной симметрией и невращательной симметрией (вращательно-симметричные
и невращательно-симметричные)4.1 Общие сведения
Деление погрешностей на эти две группы составляющих является надежным практическим способом получения простейшими средствами полезной информации. Этим способом следует пользоваться с осторожностью, поскольку он не позволяет определить вращательно-симметричные погрешности испытуемого объекта. Однако практически очень часто они не влияют на результаты измерений, равно как и невращательно-симметричные.
В 4.2—4.4 описана процедура деления погрешностей измеренного волнового фронта оптических элементов на упомянутые составляющие с целью определения абсолютных значений невращательносимметричных погрешностей при измерениях характеристик поверхностей испытуемых образцов.
Описываемая процедура применима ко всем оптическим поверхностям с вращательносимметричной формой, включая плоскости, сферы и асферические поверхности, а также к оптическим элементам и системам, работающим на пропускание. Процедура неприменима к оптическим поверхностям, форма которых не обладает вращательной симметрией, например к внеосевым асферическим поверхностям. Более того, процедура не позволяет определить абсолютные значения вращательносимметричных погрешностей испытуемого объекта.
4.2 Принцип
Используемые при измерениях формы волновых фронтов двухпучевые интерферометры всегда определяют разность между погрешностями измерения волнового фронта контролируемого объекта и погрешностями волнового фронта самого интерферометра, которые не могут быть отделены друг от друга путем однократного измерения. Например, погрешности интерферометра включают погрешности эталонной поверхности, погрешности пропускающей сферической поверхности или компенсирующих оптических элементов. Для определения погрешностей контролируемого образца используются так называемые вторичные эталоны (reference standards) или методы «абсолютных испытаний» (absolute tests). Однако для практического применения существуют и другие хорошо известные процедуры. Одна из них, не требующая применения дополнительных оптических элементов, называется методом «трех положений» [1] и используется при испытаниях сфер. Однако для объектов других типов (например, плоскостей, выпуклых сфер, пропускающих оптических, в том числе асферических элементов) нет простых, недорогих, доступных процедур выполнения «абсолютного контроля».
«Квазиабсолютный контроль» по определению невращательно-симметричных погрешностей волнового фронта может базироваться на измерениях контролируемого объекта под различными углами 0 его поворота (см. рисунок 1), и тогда погрешность определяется по формуле
P(r,Q) = PR(r) + PNR(r,Q), (1)
где PR(r) — вращательно-симметричная составляющая;
PNR(r, 0) — невращательно-симметричная составляющая.
Соотношение между погрешностью поверхности S и измеренной погрешностью волнового фронта Р описывается выражением Р= 2S.
Если погрешность интерферометра также разделить на вращательно-симметричную TR(r) и невращательно-симметричную TNR(r, 0) составляющие, то погрешность измерений формы волнового фронта представится в виде
W=TR + PR + PNR (2)
В [2—4] показано, что вращение волнового фронта с фиксацией в N (где N = 2, 3...) эквидистантно расположенных положениях (2n/N — интервал между ними) с последующим усреднением данных сводит к нулю все невращательно-симметричные составляющие за исключением тех, порядок которых равен к ■ N ■ 0, где к = 1,2... .
Это может быть использовано для выделения невращательно-симметричных погрешностей контролируемого образца путем выполнения измерений в N положениях с усреднением результатов. Математически это записывается в виде Wv / = 1, ..., /V:
3
а) Оптическая схема б) Интерферограмма
эксперимента
1 — погрешность поверхности S(r, 0); 2 — идеальная поверхность; 3 — линза; 4 — плоская волна на выходе интерферометра
Рисунок 1 — Оптическая схема интерференционного эксперимента по контролю выпуклой отражающей поверхности
Щ =TR + tnr +pr+ P/vr; (3)
W2=TR+ TNR +PR+ PfiR и т. д.
После усреднения полученных результатов с целью исключения (или, по крайней мере, значительного уменьшения) невращательно-симметричных составляющих (за исключением имеющих порядок к- N • 0) получаем:
WA = TR + TNR + PR + PNRd ■ (4)
Таким образом,
W,-Wa=Pnr-p№q, (5)
что подлежит вычитанию из любого значения 1/Ц и позволяет выявить невращательно-симметричную составляющую, за исключением той, которая имеет порядок к - N ■ 0.
Если данные однократных измерений повторяются перед усреднением, то
WB = TR + TNRd + PR + PNR (6)
И
Щ - WB = TNR - , (7)
что и является невращательно-симметричной составляющей суммарной погрешности интерферометра за исключением той, которая имеет порядок к ■ N ■ 0.
4.3 Измерительная аппаратура
Для выполнения описываемых далее измерений и контроля необходимы:
4.3.1 Цифровой интерферометр.
4.3.2 Аттестованная измерительная установка для проведения контроля.
4.3.3 Механизм вращения контролируемого образца.
4.3.4 Программное обеспечение, позволяющее усреднять и дифференцировать результаты измерений формы волнового фронта.
4
ГОСТ Р 8.744-2011/ISO/TR 14999-3:20054.4 Методика выполнения измерений
Контролируемый образец должен быть измерен в N > 4 равномерно расположенных угловых положениях. Последовательность операций такова:
а) измерение контролируемого образца в первом положении, зафиксированном при его вращении; регистрация результатов измерений волнового фронта с вычитанием сферической аберрации и наклона;
б) поворот контролируемого образца на угол 2ii/N, N > 4 и повторение измерения, регистрация результатов измерений;
в) повторение измерений по пункту б) во всех N положениях контролируемого образца;
г) вычисление среднего из N результатов измерений и регистрация усредненных данных;
д) вычитание полученных данных из результата измерений, полученного в пункте а), и регистрация окончательного результата измерений.
5 Измерение качества физически реализованной эталонной поверхности5.1 Плоскости5.1.1 Общие сведения
5.1.1 Общие сведения
В данном случае необходимы:
а) плоский элемент типа эталонного плоского зеркала;
б) контролируемый плоский элемент или оптическая система с плоским волновым фронтом на выходе, являющиеся объектами измерений.
Излучение источника распространяется в виде плоской волны, падающей по «нормали» на эталон и контролируемый образец. Из-за дефектов обеих поверхностей отраженный волновой фронт имеет искажения. В результате формируется интерферограмма, отражающая искажения этих волновых фронтов.
Взаимная юстировка эталона и контролируемого образца позволяет пользователю изменять интерференционную картину:
- путем наклона можно увеличивать или уменьшать чувствительность измерений, меняя расстояние между полосами (интервал между двумя полосами соответствует градиенту УА на поверхности образца);
- путем перемещения вдоль оптической оси опорного зеркала можно зарегистрировать набор интерференционных картин с различным сдвигом полос, по которым можно выделить небольшие и локальные дефекты.
Поскольку пучки отражаются лишь один раз от эталонного зеркала и от контролируемого образца, то по интерференционной картине трудно обнаружить небольшой дефект на образце. Следует помнить, что интерферометр Майкельсона без автоматической расшифровки интерферограмм не способен выявлять дефекты поверхности с разрешением по глубине, лучшим, чем Х/10.
5.1.2 Измерение, базирующееся на эталоне плоской поверхности
5.1.2.1 Эталонная плоскость
Для многих приложений эталон плоской поверхности может считаться идеальным, если его качество, по крайней мере, в 10 раз более высокое, чем у контролируемого образца. Поэтому можно считать идеальной интерферограмму, созданную волновым фронтом, полученным в результате отражения излучения таким эталоном, а интерферограмму, полученную в результате отражения излучения контролируемым образцом, — искаженную его дефектами. Видимые невооруженным глазом искажения интерферограммы отражают аберрации волнового фронта, определяющие качество поверхности контролируемого образца.
Для определения размеров и координат дефектов на образце и эталоне пользователь может сравнить результаты первого измерения с результатами одного или нескольких последующих измерений, полученных при:
- перемещении эталона относительно образца в плоскости его поверхности;
- вращении эталона относительно образца вокруг оптической оси.
При этом пользователь может (см. рисунки 2 и 3):
- выполнять более одного перемещения в более чем одном направлении;
- выполнять более одного вращения;
- комбинировать перемещение(я) с вращением(ями).
5
|
S M + S |
|
М — эталон в начальном положении; S — образец в начальном положении; М + S— начальная интерференционная картина; 1 — неоднородность образца на начальной интерференционной картине |
|
М |
|
М9 S Mg S |
|
б) Положения после перемещения эталона |
М' — эталон после перемещения; S — образец; M'S — вторая интерференционная картина; 2— неоднородность образца на второй интерференционной картине
|
Рисунок 2 — Интерференционные картины и влияние перемещения Mi Si Mi + Si |
а) Начальные положения
|
M — эталон в начальном положении; Mi— индекс эталона; S — начальное положение образца; S,- — индекс образца; М + S, Mi + Si— начальная интерференционная картина; 1 — неоднородность образца на начальной интерференционной картине |
б) Положения после поворота образца
А — эталон; В — образец после поворота; С — вторая интерференционная картина;
2— неоднородность образца на второй интерференционной картине
Рисунок 3 — Интерференционные картины и влияние вращения
Путем сравнения различных интерференционных картин, соответствующих разному взаимному расположению эталона и образца, пользователь может определить местонахождение и размеры дефектов (при этом необходимо помнить, что интерферограмма отображает алгебраическую сумму аберраций).
5.1.2.2 Определение качества эталона плоской поверхности
Очевидно, что оптический элемент, используемый в качестве эталона плоской поверхности, должен быть аттестован. Проверка его качества производится в соответствии с рекомендациями, содержащимися в данном подразделе.