ГОСТ Р ИСО 5479-2002
Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения
Устанавливает методы и критерии для проверки отклонения распределения вероятностей от нормального распределения при независимых наблюдениях
Идентичен (IDT) ISO 5479:1997
Оглавление
1 Область применения
2 Нормативные ссылки
3 Определения и обозначения
4 Общие положения
5 Графический метод
6 Направленные критерии
7 Совместный критерий, использующий статистики квадратного корня из b с индексом 1 и b с индексом 2 (многонаправленный критерий)
8 Многосторонние критерии
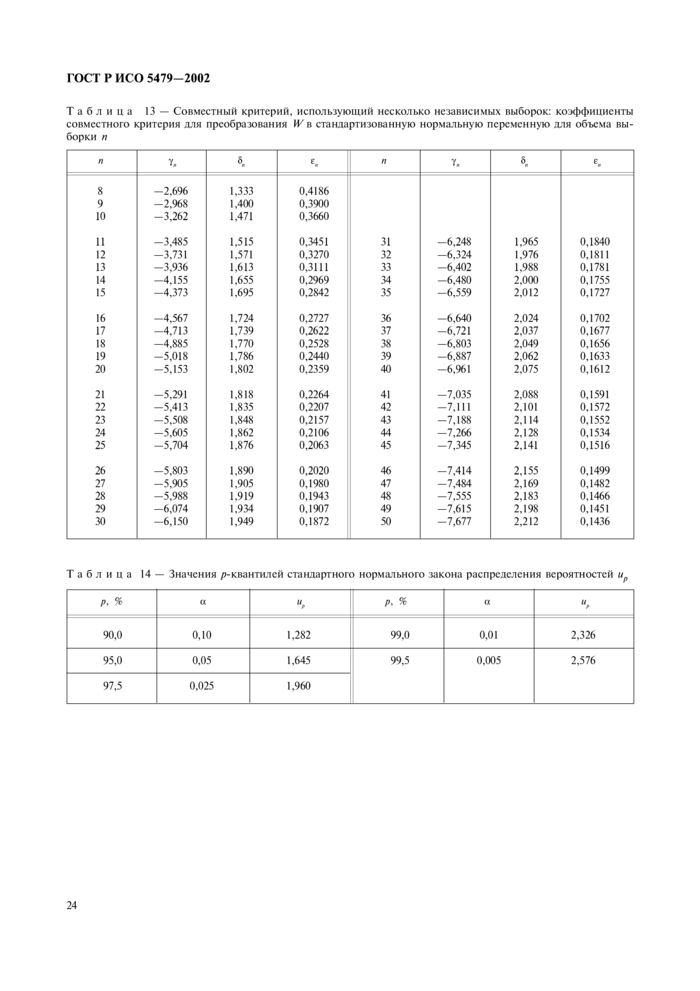
9 Совместный критерий, использующий несколько независимых выборок
10 Статистические таблицы
Приложение А Бланк бумаги для нормальных вероятностных графиков
31 страница
| Дата введения | 01.07.2002 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Строительство
- Раздел Экология
Организации:
| 22.01.2002 | Утвержден | Госстандарт России | 25-ст |
|---|---|---|---|
| Разработан | ТК 125 Статистические методы в управлении качеством продукции | ||
| Издан | ИПК Издательство стандартов | 2002 г. |
Statistical methods. Tests for departure of the probability distribution from the normal distribution
ГОСТ Р 50779.10-2000Статистические методы. Вероятность и основы статистики. Термины и определения. Заменен на ГОСТ Р ИСО 3534-1-2019.- Федеральный закон 162-ФЗ О стандартизации в Российской Федерации
- ГОСТ Р ИСО 3534-1-2019 Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7
стр. 8
стр. 9
стр. 10
стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18
стр. 19

стр. 20
стр. 21
стр. 22
стр. 23
стр. 24
стр. 25
стр. 26
стр. 27
стр. 28

стр. 29

стр. 30
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ПРОВЕРКА ОТКЛОНЕНИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ОТ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
БЗ 11-2001/273
И иа н ис официал ьнос
ГОССТАНДАРТ РОССИИ Москва
Предисловие
1 РАЗРАБОТАН И ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции*;
Акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (АО НИИ КД)
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 22 января 2002 г. № 25-ст
3 Настоящий стандарт представляет собой аутентичный текст международного стандарта ИСО 5479 —97 «Статистическое представление данных. Проверка отклонения распределения вероятностей от нормал ьного распределения *
4 ВВЕДЕН ВПЕРВЫЕ
© И ПК Издательство стандартов. 2002
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Госстандарта России
ГОСТ Р И СО 5479- 2002
Содержание
1 Область применения.................................... 1
2 Нормативные ссылки.................................... 1
3 Определения и обозначения................................ 1
4 Общие положения..................................... 2
5 Графический метод..................................... 3
6 Направленные критерии................................... 8
7 Совместный критерий, использующий статистики и Ь2 (многонаправленный критерий) 11
8 Многосторонние критерии.................................. II
9 Совместный критерий, использующий несколько независимых выборок........... 16
10 Статистические таблицы.................................. 17
Приложение А Бланк бумаги для нормальных вероятностных графиков............ 25
III
Введение
Настоящий стандарт устанавливает критерии, с помощью которых можно проверить, подчиняется ли генеральная совокупность данных нормальному закону распределения. Это следующие виды критериев: графический метод, направленный критерий, многонаправленный критерий, многосторонний критерий, совместный критерий для нескольких независимых выборок.
Целью настоящего стандарта является — привести критерии, удобные для использования специалистами в промышленности для проверки на нормальность различных данных в ходе проведения измерений, контроля и испытаний.
В настоящем стандарте рассматриваются способы построения статистик и правила принятия решений для критериев проверки на нормальность.
IV
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ПРОВЕРКА ОТКЛОНЕНИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ОТ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Statistical methods. Tests for departure of the probability distribution from the normal distribution
Дата введения 2002-07—01
1 Область применения
1.1 Настоящий стандарт устанавливает методы и критерии для проверки отклонения распределения вероятностей от нормального распределения при независимых наблюдениях.
1.2 Применение критерия на отклонение от нормального распределения необходимо во всех случаях, когда есть сомнение, нормально ли распределены наблюдения. В случае робастных методов (то есть таких, что результаты наблюдений незначительно изменяются, когда реальное распределение вероятностей наблюдений ненормально) критерий на отклонение от нормального распределения не применяют. Например случай, когда выборочное среднее арифметическое единственной случайной выборки, полученной в результате наблюдений, необходимо сопоставить с данным теоретическим значением с использованием /-критерия.
1.3 Необязательно использовать такой критерий при каждом обращении к статистическим методам. основанным на гипотезе нормальности. Существуют случаи, когда в нормальности распределения наблюдений нет сомнения: есть теоретические (например физические) обоснования, подтверждающие гипотезу, или гипотезу считают приемлемой согласно априорной информации.
1.4 Кртерни на отклонение от нормального распределения, установленные в настоящем стандарте. в основном рассчитаны на полные, несгруппированные данные.
2 Нормативные ссылки
В настоящем стандарте использована ссылка на следующий стандарт:
ГОСТ Р 50779.10-2000 (ИСО 3534.1-93) Статистические методы. Вероятность и основы статистики. Термины и определения
3 Определения и обозначения
3.1 Определения
В настоящем стандарте применяются термины с соответствующими определениями по ГОСТ Р 50779.10.
3.2 Обозначения
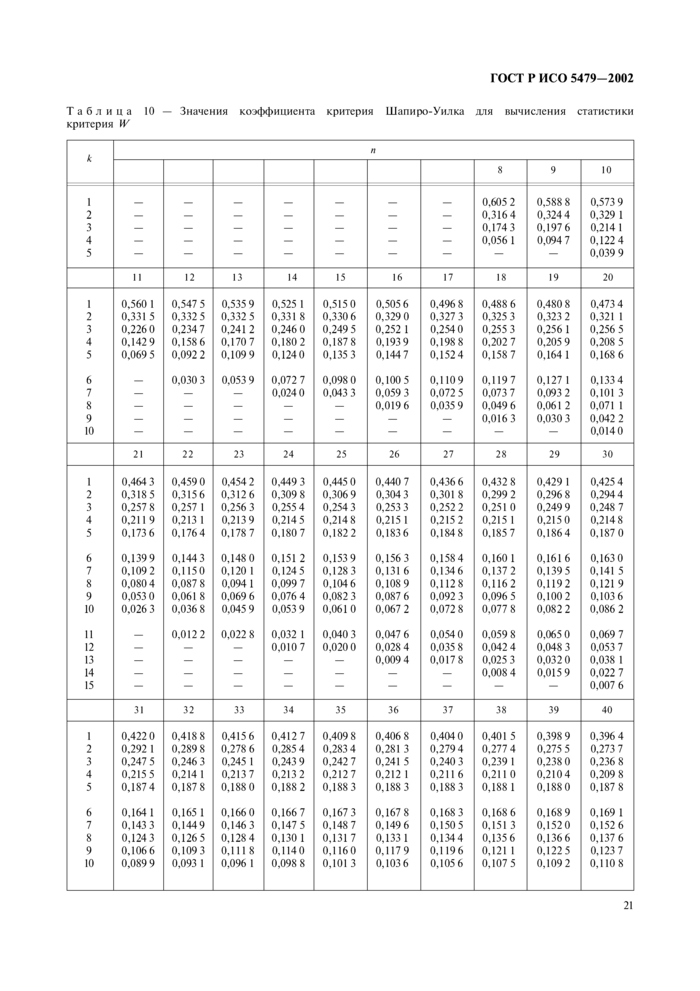
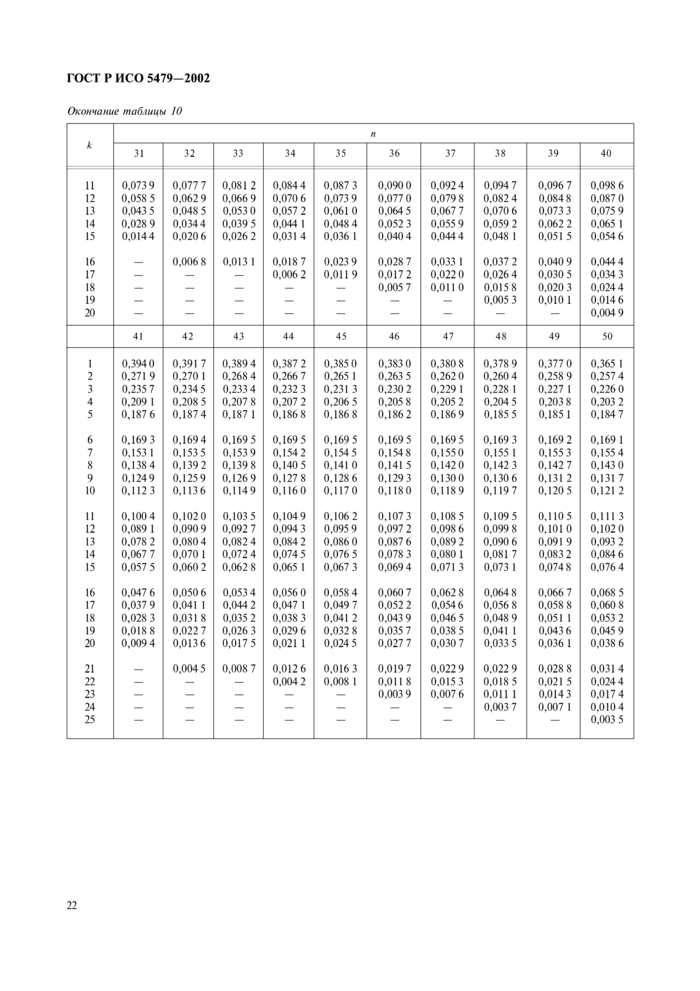
В настоящем стандарте использованы следующие обозначения: ак — коэффициент критерия Шапиро-Уилка;
Л\ В — вспомогательные величины для критерия Эппса-Палли;
Ь2 — эмпирическая кривизна;
%i^ — эмпирическая асимметрия;
Издание официальное
"о
Я,
т,
л
Р
Р
Л
5
Т
Г„
W
ч
X
х
XJ
хк
х
а
Р
Р2
P>-i
Vaу. б; е
у ; 5 ; с
1ц' 11’ и
м
м-
и;
М4
математическое ожидание;
вспомогательная величина для совместного критерия, иснолыуюшего несколько независимых выборок; число последовательных выборок; нулевая гипотеза; альтернативная гипотеза;
порядковый номер значений .г в выборке, упорядоченной в порядке неубывания; выборочный центральный момент порядка}\ объем выборки;
вероятность, свя занная с />-квантилью распределения вероятностей; вероятность;
вероятность, связанная с Хк\
вспомогательная величина для критерия Шапиро-Уилка;
статистика критерия;
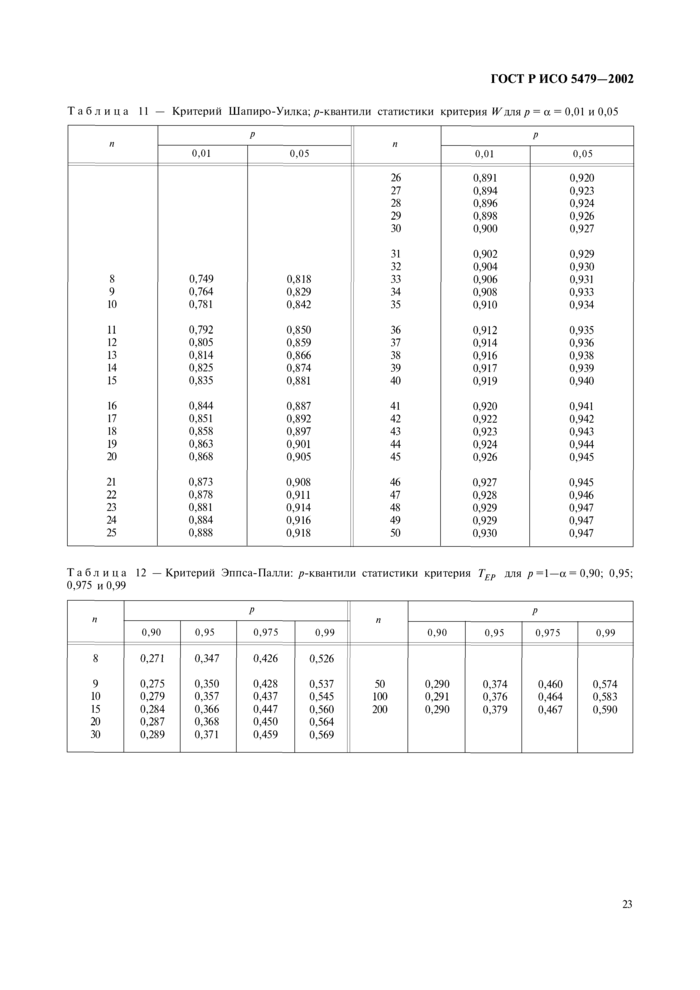
статистика критерия Эппса-Палли;
р-квантиль стандартного нормального распределения;
вспомогательная величина для совместного критерия, использующего несколько
независимых выборок;
статистика критерия Шапиро-Уилка;
вспомогательная величина для совместного критерия, использующего несколько
независимых выборок;
случайная переменная;
значение случайной переменной А";
у-с значение в выборке, упорядоченной в порядке неубывания; к-с значение в выборке, упорядоченной в порядке неубывания;
среднее арифметическое; уровень значимости; вероятность ошибки второго рода; кривизна совокупности; эксцесс совокупности;
асимметрия совокупности;
вспомогательные величины для совместного критерия, использующего несколько независимых выборок;
коэффициенты совместного критерия, использующего несколько независимых выборок;
математическое ожидание (центральный момент первого порядка); дисперсия совокупности (центральный момент второго порядка); центральный момент совокупности третьего порядка: центральный момент совокупности четвертого порядка;
стандартное отклонение совокупности (о = )•
4 Общие положения
4.1 Существуют различные критерии на отклонение от нормальности. В настоящем стандарте установлены графические методы, моментные критерии, регрессионные критерии и критерии характеристических функций. Критерии хи-квадрат подходят только для сгруппированных данных, и так как группирование приводит к потере информации, в данном стандарте они нс рассмотрены.
4.2 Если о выборке нет дополнительной информации, рекомендуется сначала построить нормальный вероятностный график, то есть построить кумулятивную функцию распределения значений, полученных в результате наблюдений, на бумаге для нормальных вероятностных графиков с осями координат, в которых кумулятивная функция нормального распределения представлена прямой линией.
ГОСТ I» ИСО 5479-2002
Этот метод, установленный в разделе 5. позволяет сразу видеть, близко ли полученное распределение к нормальному. Используя данную дополнительную информацию, необходимо решить, какой критерий можно применить: направленный, регрессионный, критерий характеристической функции или никакой. Такое графическое представление нельзя рассматривать как строгий критерий, но даваемая им суммарная информация яалястся существенным дополнением к любому критерию на отклонение от нормального распределения. В случае отклонения нулевой гипотезы зга информация даст возможность определить тип альтернативной гипотезы, которая могла бы быть применима.
4.3 Критерий на отклонение от нормального распределения имеет нулевую гипотезу, состоящую в том. что выборка содержит п значений независимых наблюдений, подчиняющихся одному и тому же нормальному распределению. Он заключается в вычислении функции Гот этих значений, называемой статистикой критерия. Нулевую гипотезу о нормальности распределения принимают или отклоняют в зависимости от того, лежит ли статистика Г в области ожидаемых значений, соответствующих норма! ьному расп редел ен и ю.
4.4 Критическая область критерия — это совокупность значений Г. ведущих к отклонению нулевой гипотезы. Уровень значимости критерия — это вероятность Г получения значения Г в критической области, когда нулевая гипотеза верна. Этот уровень дает вероятность ошибочного отклонения нулевой гипотезы (вероятность ошибки первого рода).
Граница критической области (или в случае двустороннего критерия — границы критической области) — это критическое значснне(ння) статистики критерия.
4.5 Мощность критерия — это вероятность отклонения нулевой гипотезы, когда она неверна. Высокая мощность соответствует низкой вероятности ошибочного применения нулевой гипотезы (вероятности ошибки второго рода).
Мощность критерия (то есть для данной ситуации вероятность, что нулевая гипотеза о нормальности распределения будет отклонена, если она неверна) возрастает с ростом числа наблюдений. Например. отклонение от нормального распределения, которое могло быть очевидным при использовании критерия с большой выборкой, можно нс обнаружить при том же значении критерия с меньшей выборкой.
4.6 Существуют два вида критериев на отклонение от нормального распределения: направленный критерий — когда форму этого отклонения устанавливают в альтернативной гипотезе и многосторонний критерий — когда форму отклонения в ней не устанавливают.
В направленном критерии критическую область определяют так, чтобы мощность критерия достигала максимального значения. В многостороннем Kpirrcpini необходимо отделить критическую область гак. чтобы она состояла и з значений статистики критерия, лежащих далеко от ожидаемого значения.
Если имеются предположения о форме отклонения от нормального распределения, то есть рассматривается распределение, у которого асимметрия шли кривизна отличны от свойственных нормальному распределению, то следует применить направленный критерий, так как его мощность больше, чем у многостороннего.
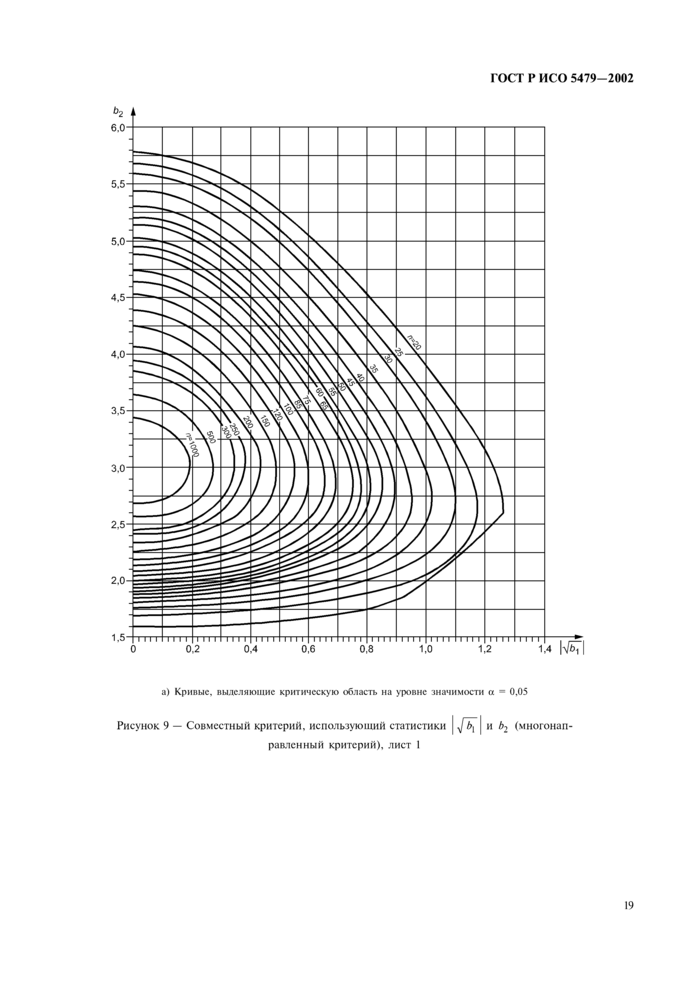
4.7 Направленный критерий является односторонним. В случае асимметрии он сдвигается к положительной или отрицательной асимметрии. Ес-ли совместно рассматривают несколько альтернативных гипотез — это критерий многонаправленный. Такие критерии используют при совместном рассмотрении ненулевых асимметрии и кривизны, отличных от свойственных нормальному распределению.
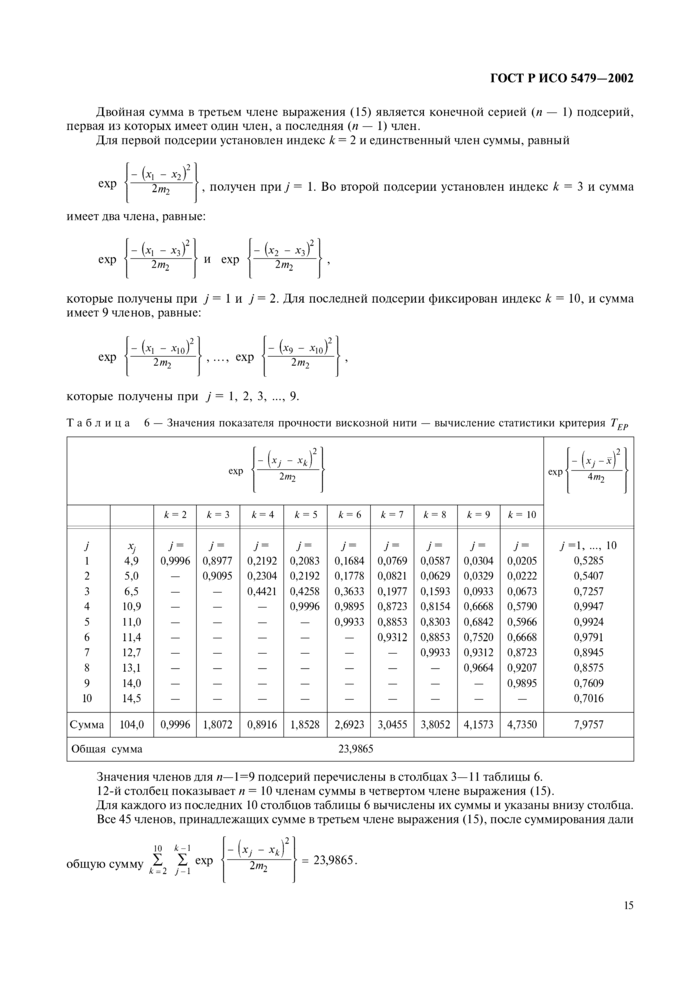
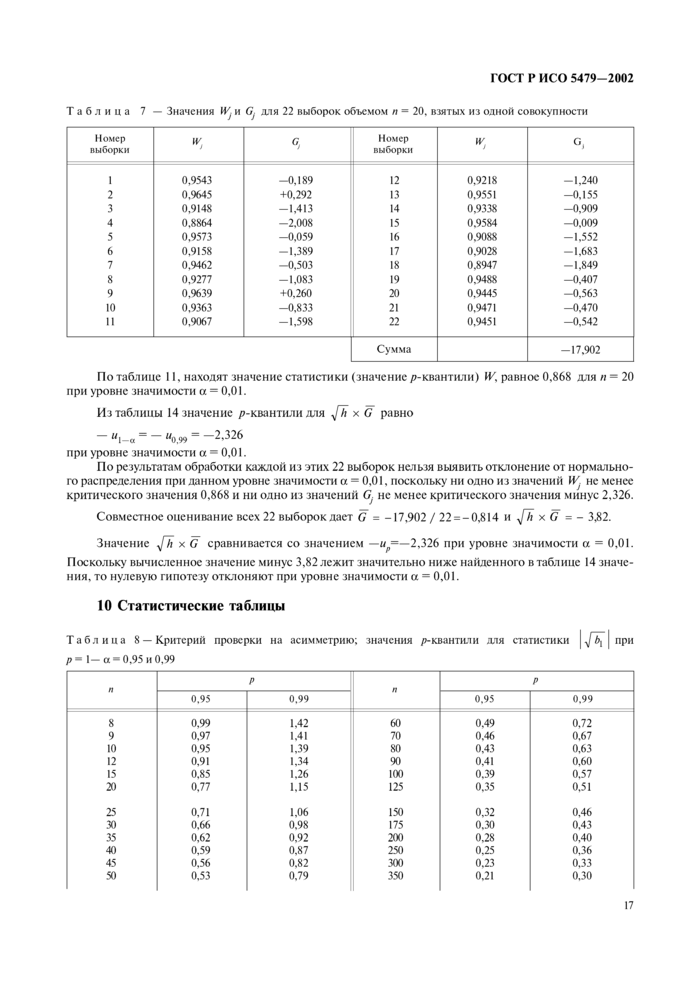
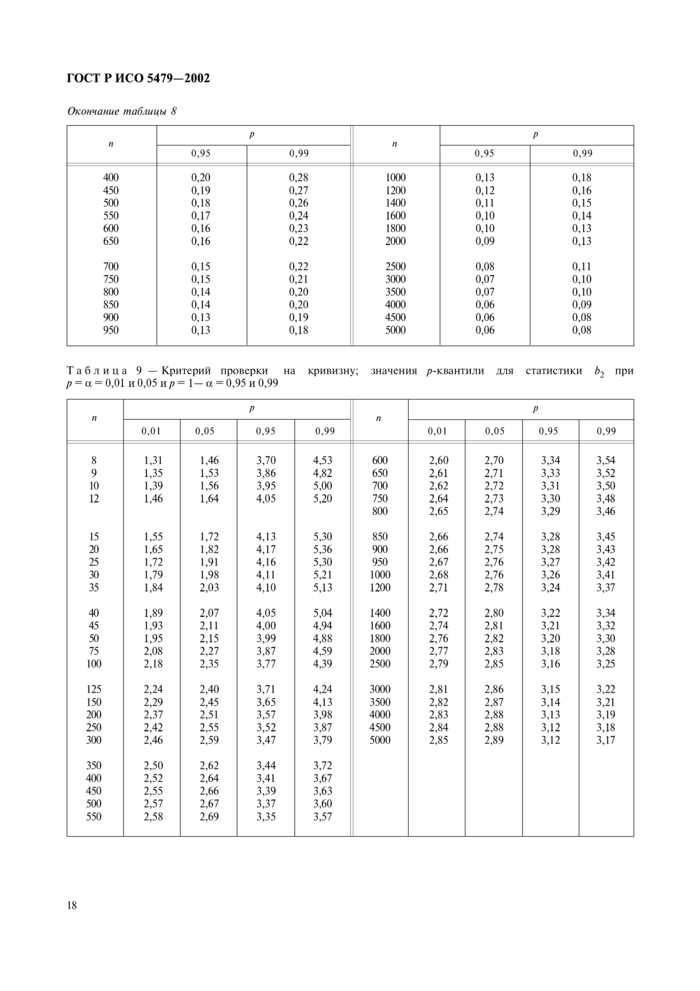
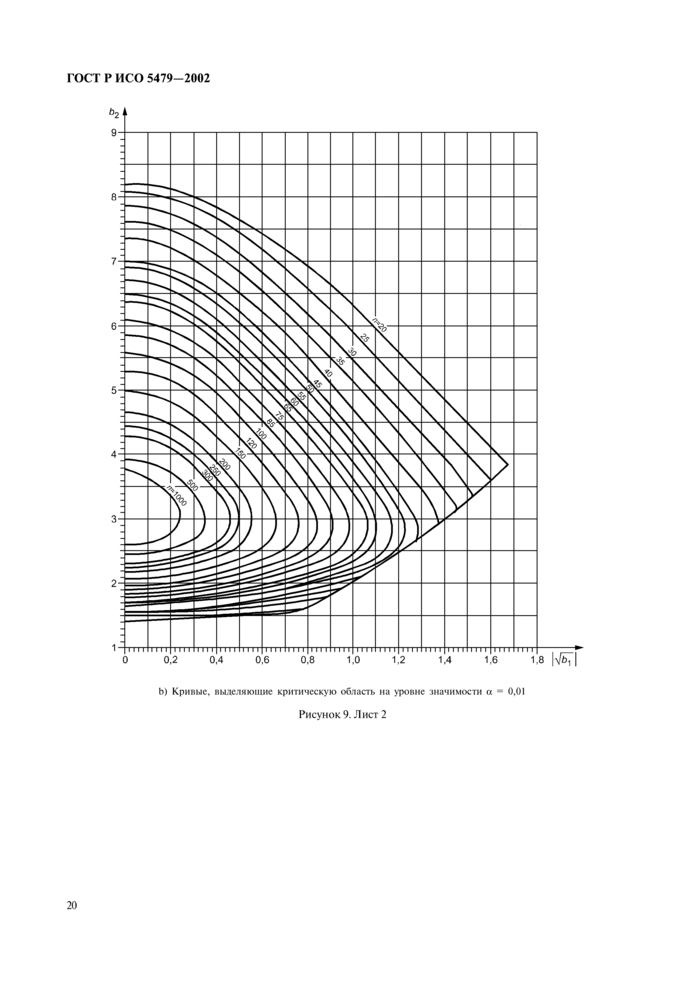
4.8 Таблицы 8—14 и рисунок 9 позволяют применять критерии аля наиболее распространенных уровней значимости а. то есть а = 0.05 и а = 0.01. До использования критерия следует установить уровень значимости. Критерий может привести к отклонению нулевой гипотезы при уровне значимости 0.05 и не отклонению той же гипотезы при уровне значимости 0,01.
4.9 При вычислении статистики критерия необходимо использовать нс менее шести значащих цифр. Значения подсовокупностей, промежуточных результатов и вспомогательных величин следует округлять не менее чем до шести значащих цифр.
5 Графический метод
5.1 Кумулятивную функцию распределения наблюденных значений строят на бумаге для нормальных вероятностных графиков. Вертикальная ось имеет нелинейную шкалу, соответствующую площади под стандартной функцией нормального распределения и размечена значениями кумулятивной относительной частоты. Другая ось имеет линейную шкалу для упорядоченных значений х. Если кумулятивная функция распределения переменной X приближается к прямой линии, то распределение переменной Л”будет нормальным.
3
Иногда эти оси меняют местами. Если выполнено нормирование переменной X, линейную шкалу можно заменить логарифмической, квадратичной, обратной или другой шкалой.
На рисунке I приведен пример бумаги для нормальных вероятностных графиков. По вертикальной оси значения кумулятивной относительной частоты даны в процентах, а по горизонтальной — произвольная линейная шкала.
Чистый бланк бумаги для нормальных вероятностных графиков приведен в приложении Л.
Если график на этой бумаге предстаатсн набором точек, которые рассеянны около прямой линии. то это даст первое подтверждение утверждению, что генеральная совокупность, из которой взята выборка, подчиняется нормальному закону распределения.
Этот подход важен тем, что даст наглядную информацию по типу отклонения от нормального распределения.
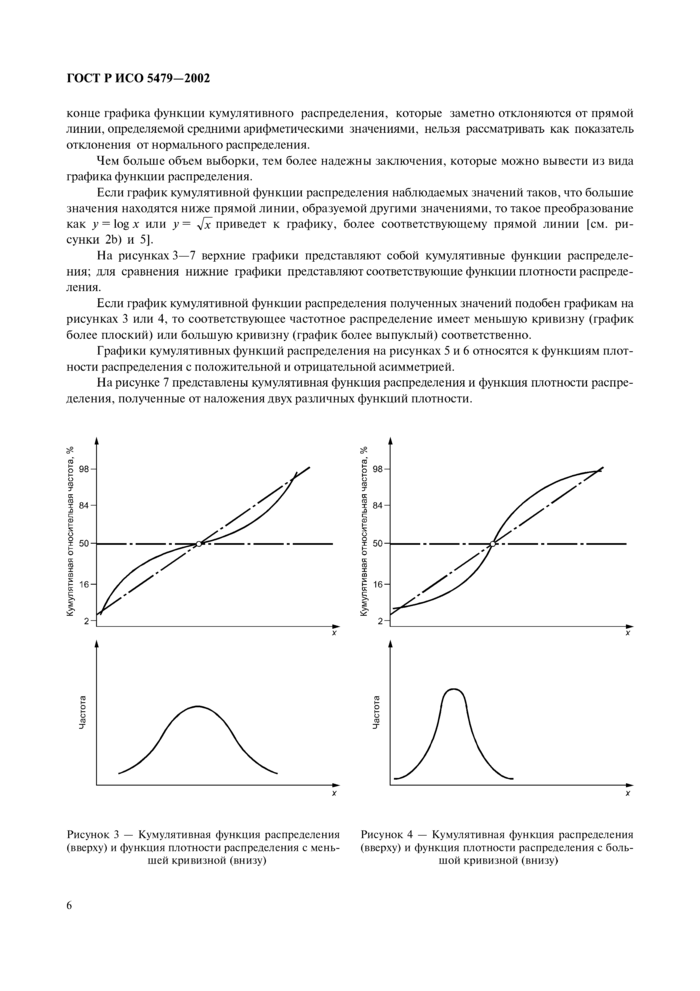
Если график показывает, что данные подчинены другому распределению, нс имеющему отношения к нормальному (например график кумулятивной функции распределения такой, как на рисунке 5 или 6). то в некоторых случаях к нормальному распределению можно перейти с помощью специального преобразования.
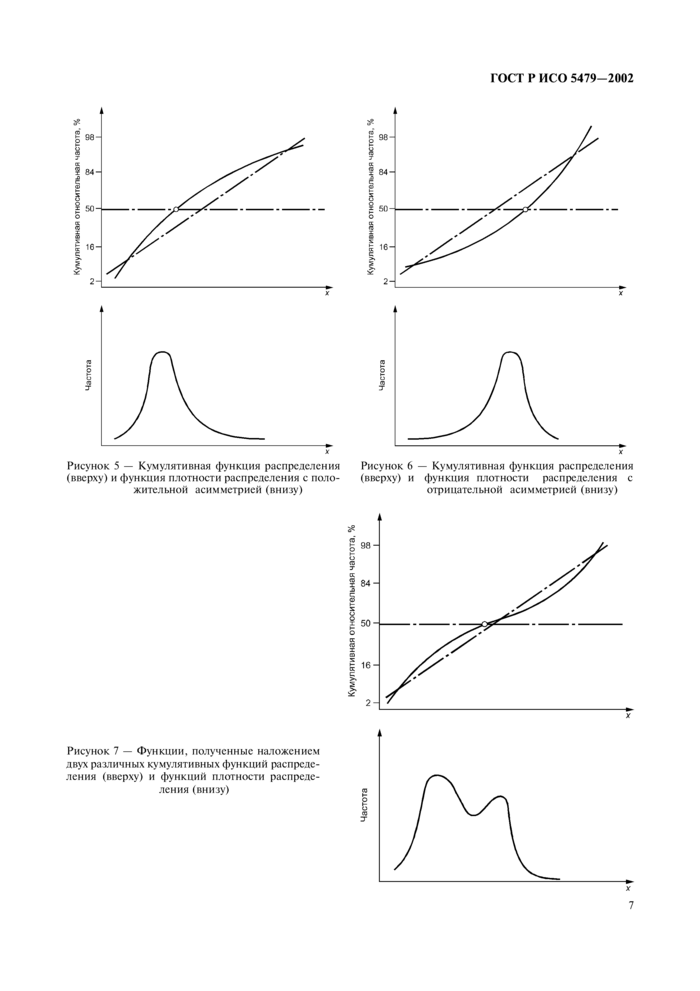
Если график показывает, что данные не подчиняются простому однородному распределению, а скорее всего принадлежат смеси двух или нескольких однородных подсовокупностей (например, если график кумулятивной функции распределения такой, как на рисунке 7), то рекомендуется выявить подсовокупности и анализ каждой из них проводить отдельно.
Этот графический метод нс яатястся критерием на отклонение от нормального распределения в строгом смысле. Например, в случае малых выборок с его помощью можно получить выраженные кривые нормальных распределений, но для больших выборок кривые могут представлять ненормальные распределения.
4
5.2 Графическая процедура состоит в расположении наблюденных значений (лг,. х2.....хя) в
неубывающем порядке и затем в нанесении значений вероятности Рк, рассчитанных по формуле
Рк ш (к -3/8)/(я + 1/4), (I)
на бумагу для нормальных вероятностных графиков (где к — порядковый номер х: к - I.....п).
Примечание! — Часто вместо формулы (1) применяют следующие формулы: Рк ш (к — 1/2)/п и Рк ■ к (л + I). Применение данных формул не рекомендуется, так как они дают плохую аппроксимацию нормальной функшш распределения ожидаемой порядковой статистики F[E (А^)).
|
Таблица I — Значения хк серии из 15 независимых наблюдений и соответствующие им значения lg <10дг4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
П р и м с ч а н и с 2 — В таблице I и последующих примерах единицы величин опушены, так как это несущественно для рассматриваемых критериев в данном стандарте. |
5.3 Пример использования бумаги для нормальных вероятностных графиков показан на рисунке 2.
В таблице I приведены значения хк в порядке неубывания как результат серии из 15 независимых наблюдений при испытаниях на усталость вращающегося соединения.
Серию точек, показанную на рисунке 2а) получают на основе значений вероятностей Рк ш (к —3/8)/(/г + 1/4) и хк. И з графика видно, что эти точки не образуют прямой линии. Если хк заменить на lg (10 хк). то новый график на рисунке 2Ь) близок к прямой линии. Из этого следует, что гипотеза нормального распределения для логарифма наблюдений адекватна.
5.4 Рассеяние полученных экстремальных значений больше, чем у средних арифметических значений, поэтому шкала кумулятивной относительной частоты расширяется к краям. Наличие небольшого числа значений на любом
5
копне графика функции кумулятивного распределения, которые заметно отклоняются от прямой линии, определяемой средними арифметическими значениями, нельзя рассматривать как показатель отклонения от нормального распределения.
Чем больше объем выборки, тем более надежны заключения, которые можно вывести из вида графика функции распределения.
Если график кумулятивной функции распределения наблюдаемых значений таков, что большие значения находятся ниже прямой линии, образуемой другими значениями, то такое преобразование как у = log л или у = -Jx приведет к графику, более соответствующему прямой линии |см. рисунки 2Ь) и 5J.
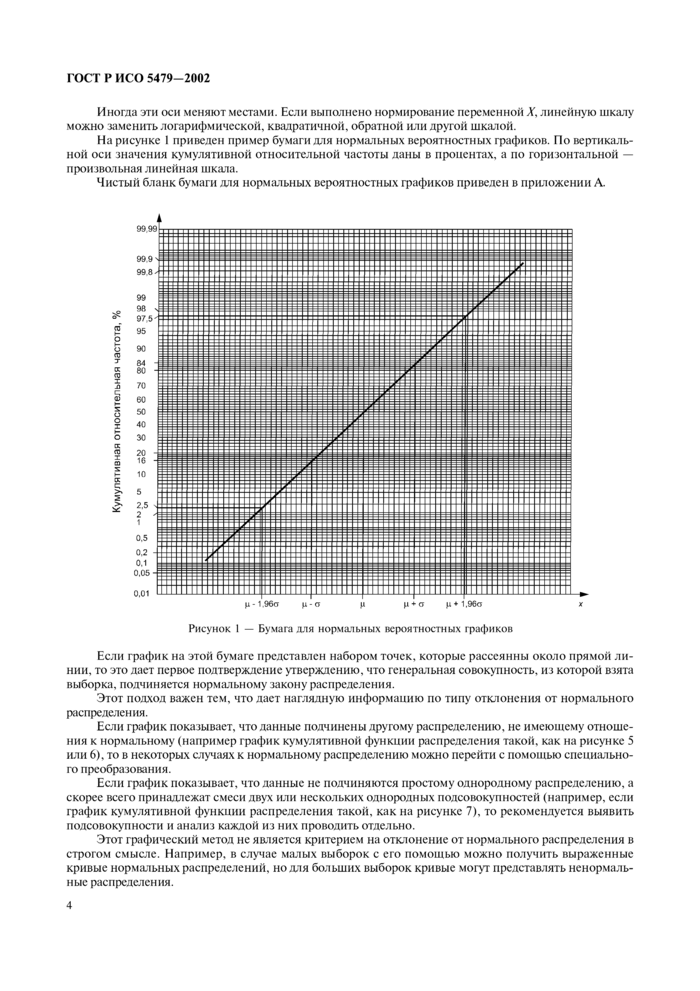
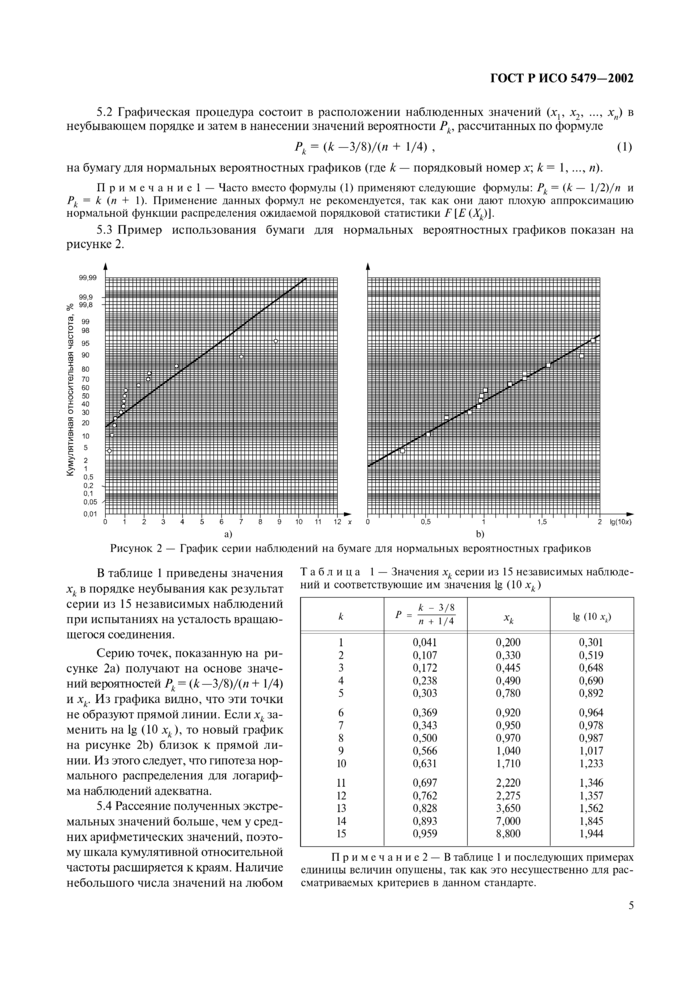
На рисунках 3—7 верхние графики представляют собой кумулятивные функции распределения; для сравнения нижние графики представляют соответствующие функции плотности распределения.
Если график кумулятивной функции распределения полученных значений подобен графикам на рисунках 3 или 4. то соответствующее частотное распределение имеет меньшую кривизну (график более плоский) или большую кривизну (график более выпуклый) соответственно.
Графики кумулятивных функций распределения на рисунках 5 и 6 относятся к функциям плотности распределения с положительной и отрицательной асимметрией.
На рисунке 7 представлены кумулятивная функция распределения и функция плотности распределения. полученные от наложения двух различных функций плотности.
Рисунок 3 — Кумулятивная функция распределения Рисунок 4 — Кумулятивная функция распределения (вверху) и функция плотности распределения с мень- (вверху) и функция плотности распределения с большей кривизной (внизу) шой кривизной (внизу)