ГОСТ Р ИСО 3758-2007
Изделия текстильные. Маркировка символами по уходу
- устанавливает систему графических символов, предназначенных для использования при маркировке текстильных изделий, несущих информацию, предупреждающую необратимое повреждение в процессе ухода за текстилем;
- определяет использование этих символов при маркировке.
В стандарте охвачены следующие виды домашней обработки: стирка, отбеливание, глажение и сушка после стирки. Включены также виды профессиональной обработки - сухая и мокрая чистки; исключено промышленное глажение.
Стандарт применим ко всем текстильным изделиям в том виде, в каком они поставлены потребителю.
- Заменяет ГОСТ Р ИСО 3758-99 «Изделия текстильные. Маркировка символами по уходу» ИУС 10-2007
Стандарт идентичен международному стандарту ИСО 3758:2006 "Изделия текстильные. Маркировочные обозначения на этикетках с правилами по уходу"
Оглавление
1 Область применения
2 Термины и определения
3 Изображение и значение символов
4 Нанесение и применение символов
Приложение А (справочное) Характеристики и доступные методы испытаний для правильного выбора символов по уходу
Приложение В (справочное) Региональная и национальная практика маркирования символами по уходу
Приложение С (справочное) символы для естественной сушки
Приложение D (справочное) Примеры дополнительных надписей
Приложение Е (справочное) Сведения о соответствии национальных стандартов Российской Федерации ссылочным международным стандартам
20 страниц
| Дата введения | 01.07.2008 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Завершение срока действия | 01.01.2014 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Экология
Организации:
| 31.07.2007 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 198-ст |
|---|---|---|---|
| Разработан | ОАО ВНИИС | ||
| Разработан | ТК 412 Текстиль | ||
| Издан | Стандартинформ | 2007 г. |
Textiles. Care labelling code using symbols
ГОСТ Р ИСО 105-D01-99Материалы текстильные. Определение устойчивости окраски. Часть D01. Метод определения устойчивости окраски к действию химической чистки. Заменен на ГОСТ Р ИСО 105-D01-2011.- ГОСТ Р ИСО 105-A01-99 Материалы текстильные. Определение устойчивости окраски. Часть А01. Общие требования к проведению испытаний
- ГОСТ Р ИСО 105-A02-99 Материалы текстильные. Определение устойчивости окраски. Часть А02. Серая шкала для оценки изменения окраски
- ГОСТ Р ИСО 105-A03-99 Материалы текстильные. Определение устойчивости окраски. Часть А03. Серая шкала для оценки степени закрашивания
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9
стр. 10

стр. 11

стр. 12
стр. 13
стр. 14
стр. 15

стр. 16

стр. 17

стр. 18

стр. 19
стр. 20
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
НАЦИОНАЛЬНЫЙ
СТАНДАРТ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ГОСТ Р исо
3758-
2007
ИЗДЕЛИЯ ТЕКСТИЛЬНЫЕ
Маркировка символами по уходу
ISO 3758:2006 Textiles — Care labelling code using symbols
(IDT)
Издание официальное
IT)
CO
N
О
о
7
h-
m
ш
Москва
Стандартинформ
2007
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации — ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Техническим комитетом ТК 412 «Текстиль», Открытым акционерным обществом «Всероссийский научно-исследовательский институт сертификации» (ОАО «ВНИИС») на основе аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением технического регулирования и стандартизации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 31 июля 2007 г. № 198-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 3758:2006 «Изделия текстильные. Маркировочные обозначения на этикетках с правилами по уходу» (ISO 3758:2006 «Textiles — Care labelling code using symbols»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных (региональных) стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении Е
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
© Стандартинформ, 2007
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
|
Символ |
Режим ухода за текстилем |
|
ш |
Чистка запрещена |
|
® |
Профессиональная мокрая чистка; обычный режим |
|
® |
Профессиональная мокрая чистка; мягкий режим |
|
® |
Профессиональная мокрая чистка; очень мягкий режим |
4 Нанесение и применение символов
4.1 Нанесение символов
Символы в соответствии с разделом 3 должны быть, по возможности, нанесены либо непосредственно на изделие, либо на этикетку. Когда это сделать невозможно, достаточно привести инструкцию по уходу только на упаковке.
Этикетки должны быть сделаны из подходящего материала с устойчивостью к обработке, указанной на этикетке, по крайней мере равной устойчивости того изделия, к которому они прикреплены.
Этикетки и символы должны быть достаточно большими, чтобы их было легко прочитать.
Очень важно, чтобы этикетки и символы были спроектированы таким образом, чтобы они были легко читаемы потребителем. Они должны быть постоянно прикреплены ктекстильному материалу так, чтобы они могли быть легко найдены и прочитаны потребителем. Нельзя допускать, чтобы часть символа была скрыта, например: полоса под символом зашита внутри шва.
4.2 Характеристики и методы испытаний для выбора подходящих символов
Соответствующие характеристики и методы испытаний приведены в приложении А.
4.3 Применение символов
Символы следует располагать в следующем порядке: стирка, отбеливание, сушка, глажение и профессиональный уход за текстилем. Однако в тех странах, где применение символов предписывается регламентами или торговыми марками, их взаимное расположение определяется этими регламентами или торговыми марками.
Виды обработок, указанные символами, применяют ко всему изделию.
7
Приложение А (справочное)
Характеристики и доступные методы испытаний для правильного выбора символов по уходу
А.1 Определения
А.1.1 Характеристики
В данном приложении рассмотрены характеристики, которые важны при повседневном использовании изделий из текстиля и на которые могут влиять негативным образом процедуры по уходу.
Рекомендуется, чтобы информация о воздействии процедур чистки на изделия из текстиля и их компоненты была известна потребителю раньше, чем он найдет предупреждающие этикетки.
А.1.2 Методы испытаний
А.1.2.1 Лабораторные методы
Методы испытаний с использованием лабораторного оборудования, которые воспроизводят реальные процедуры.
А.1.2.2 Машинные (полномасштабные) методы
Методы испытаний, использующие стандартизованные процедуры, подобные тем, которые применяют на практике.
А.1.2.3 Сенсорная оценка
Оценочный метод, который использует только органолептику.
А.2 Характеристики
А.2.1 Характеристики, испытываемые лабораторными методами
Устойчивость окраски. Общие принципы испытаний установлены в ИСО 105-А01. Шкалы для оценки изменений цвета и появления пятен установлены в ИСО 105-А02 и ИСО 105-А03, соответственно.
А.2.2 Характеристики, испытываемые машинными методами
Характеристики, на которые влияют стирка, барабанная сушка и сухая чистка. Надлежащие свойства могут быть определены стандартизованными методами испытаний или с помощью сенсорной оценки.
Соответствующие характеристики приведены в таблице А.1.
А.З Методы испытаний
Сводка соответствующих методов испытаний приведена в таблице А.1. Подробности лабораторных и машинных методов приведены в таблицах А.2 — А.6 для стандартизованных символов по уходу.
Могут быть приняты во внимание и другие характеристики в соответствии с материалами, структурой и применением изделий.
|
Таблица А.1 —Характеристики, метод испытаний и оценки | |||||||||||||||||||
|
ГОСТ Р ИСО 3758-2007
| ||||||||||||||||||||
|
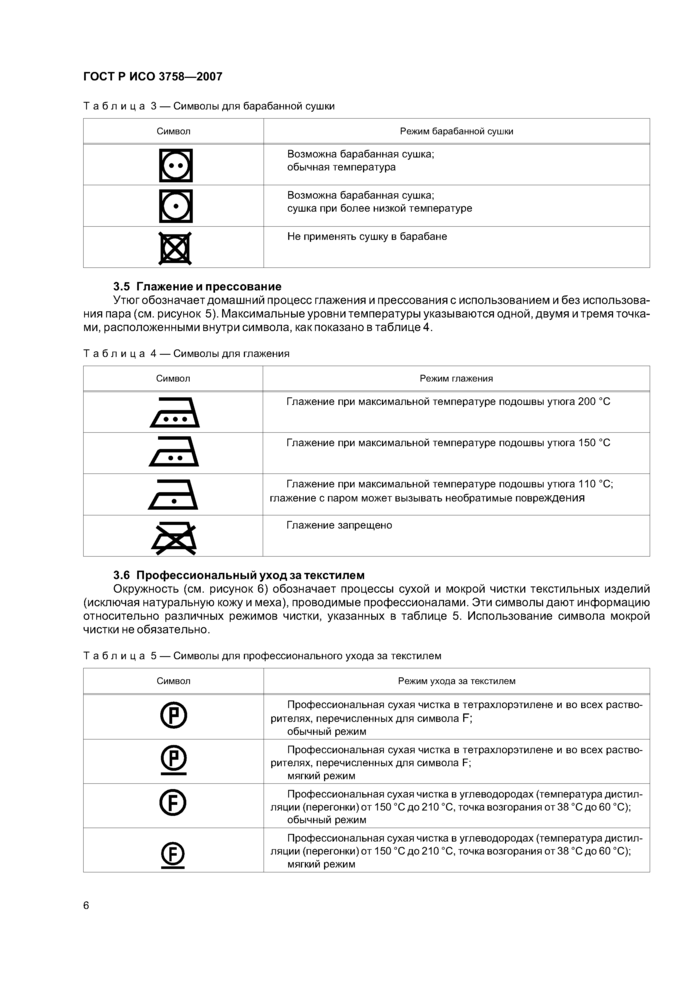
Таблица А.2 — Стирка |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Машинный метод | |||
|
Символ |
Машина типа А с фронтальной |
Машина типа В с вертикальной |
Лабораторный метод испытаний устойчивости окраски3* |
|
загрузкой с лицевой стороны с горизонтальным барабаном |
загрузкой с вертикальным барабаном | ||
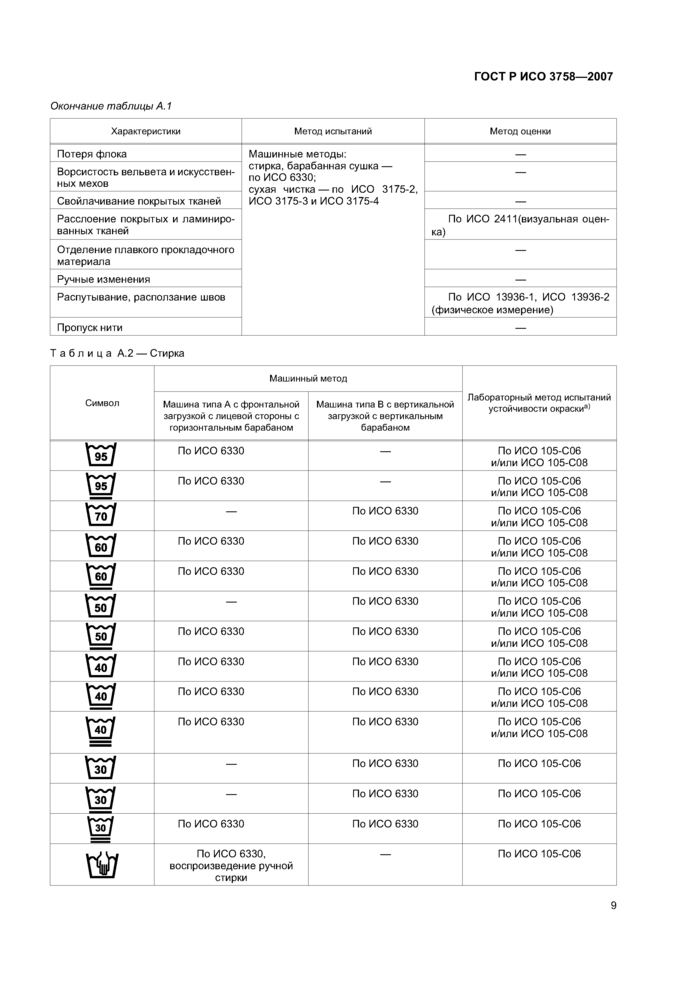
а) Смежные ткани, используемые для оценки степени закрашивания, являются многоволоконными тканями типа DW и типа TV для 40 °С, 50 °С и 60 °С, типа TV для 70 °С и одноволоконными—хлопок или полиэфир — для 95 °С. Практическая оценка появления пятен проводится в соответствии с обычной практикой для домашнего хозяйства (визуально). Другие испытания, которые могли бы быть полезны для оценки степени закрашивания смежной ткани или устойчивости окраски, описаны в ИСО 105-Е01 (устойчивость к дистиллированной воде), особенно в случае использования кислотных красителей на шерсти, полиамидах и шелке, а также в ИСО 105-Х12 (устойчивость к мокрому трению), особенно в случае применения пигментных красителей, а также в случае непрокраса ткани, которое создает проблемы при стирке.
|
Таблица А.З — Отбеливание | ||||||||||||||
| ||||||||||||||
|
а) Испытание обжигом (ААТСС ТМ 92) является дополнительным испытанием для тканей, обработанных смолами (целлюлозных и их смесей). При таком испытании не должно появляться заметное пожелтение, а потеря сопротивления к растяжению не должна превышать 25 %. | ||||||||||||||
|
Таблица А.4 — Барабанная сушка | ||||||
|
|
Таблица А.5 — Глажение | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
|
Примечание — Знак «+» — необходимость испытаний, знак «-» — испытания не требуются. | |||||||||||||||||||||||||||
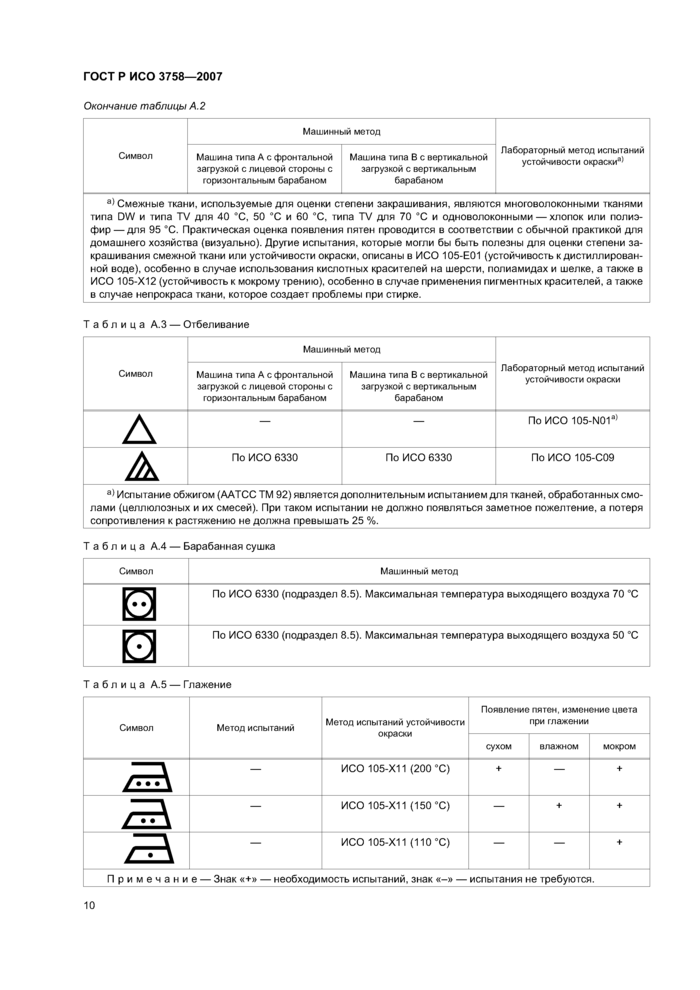
Основные принципы оценки и характеристики, которые должны быть проверены, приведены в ИСО 3175-1. Информация о содержании волокон также необходима, чтобы выбрать и интерпретировать полосы, используемые с символами для профессионального ухода за текстилем.
|
Таблица А.6 — Профессиональный уход за текстилем | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
Приложение В (справочное)
Региональная и национальная практика маркирования символами по уходу
В.1 Общие вопросы
В некоторых странах или регионах мира существуют регламенты или конкретные требования, связанные с определенными символами по уходу или с порядком расположения символов при маркировании. Ниже приведена информация, связанная с этими требованиями. Для получения более полной информации следует контактировать с национальными и региональными группами.
В.2 Региональные требования в странах GINETEX
В.2.1 GINETEX (Международная ассоциация по маркировке текстиля), созданная в 1963 г., со штаб-квартирой в Париже, разработала систему символов, не связанную с языком. Эти символы относятся к международным торговым маркам, зарегистрированным WIPO в Женеве (особенно под № 2R211 247, № 461 470 и № 492 423 — неполный перечень). GINETEX, несмотря на защиту своих прав как таковых, согласилась, чтобы ИСО использовала эту систему в международном стандарте.
В.2.2 Члены GINETEX требуют использовать защищенную торговыми марками 5-символьную маркировку.
В.2.3 Требуется, чтобы инструкции по сухой чистке всегда наносились в виде 5-символьной маркировки. Если должна быть дана информация, как по сухой, таки по мокрой чистке, символ сухой чистки должен располагаться в 5-символьной маркировке, а символ мокрой чистки должен быть расположен непосредственно под символом сухой чистки.
11
В.2.4 Символ естественной сушки использовать не обязательно.
В.2.5 Членами GINETEXявляются: Австрия, Бельгия, Чешская республика, Люксембург, Финляндия, Франция, Германия, Греция, Италия, Нидерланды, Португалия, Испания, Швейцария, Тунис и Великобритания. Для получения дополнительной информации см. web-сайт www.qinetex.org.
В.З Национальные требования в США
В.3.1 Требуется маркировка с 4-символьной инструкцией по стирке или по сухой чистке. Однако могут быть приведены оба набора инструкций. Если не дана инструкция по стирке (стирка, отбеливание, сушка и глажение), то может использоваться значительно более жесткая обработка.
В.3.2 По закону о маркировании текстильных изделий, проданных в США, при отсутствии текста инструкций (на английском языке), требуется указание температур стирки в градусах Цельсия и точек.
В.3.3 Описания и определения точечных символов для указания температур вместе с символом стирки приведены ниже.
В.3.3.1 Очень высокая температура, не более 95 °С.
Г И
L J
Рисунок В.1
В.3.3.2 Очень высокая температура, не более 70 °С.
Г И
L J
Рисунок В.2 В.3.3.3 Высокая температура, не более 60 °С.
Г 1
• • • •
L J
Рисунок В.З
В.3.3.4 Высокая температура, не более 50 °С.
Г 1
1_ J
Рисунок В.4
В.3.3.5 Умеренная температура, не более 40 °С.
Г И
• •
L J
Рисунок В.5
12
ГОСТ Р ИСО 3758-2007
В.3.3.6 Низкая температура, от 20 °Сдо 30 °С.
Г И
1_ J
Рисунок В.6
|
Таблица В.1 — Символы с точками для режимов стирки | ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
|
В.3.3.7 Для дополнительной информации см. web-сайт www.ftc.gov. |
13
Приложение С (справочное)
Символы для естественной сушки
С.1 Общие вопросы
Эти символы могут быть введены, чтобы иметь унифицированный способ повсеместно маркировать процессы естественной сушки в тех странах, которые в них нуждаются.
При использовании они должны быть помещены под 5-значной маркировкой и четко отделены от нормативных символов.
Инструкции для естественной сушки могут быть даны в виде текста или в виде символов.
С.2 Определение
Естественная сушка — это процесс, проводимый после стирки текстильного изделия, предназначенный для удаления остатков воды путем вертикальной сушки или вертикальной сушки без отжима или горизонтальной сушки на плоскости в расправленном состоянии на солнце или в тени.
С.З Описание и определение символов
Для процесса естественной сушки основным символом является квадрат, как показано на рисунке С.1.
|
Рисунок С. 1 |
Дополнительные символические элементы внутри квадрата представляют конкретные процессы вертикальной сушки, вертикальной сушки без отжима, горизонтальной сушки на плоскости в расправленном состоянии, вертикальной сушки в тени, вертикальной сушки без отжима в тени и горизонтальной сушки на плоскости в расправленном состоянии в тени, как показано в таблице С.1.
Квадрат с изогнутой линией между верхними углами квадрата представляет вертикальную сушку, при которой текстильное изделие высушивается при подвешивании его влажным на веревке или на планке внутри помещения или на улице после удаления избытка воды (отжима).
Квадрат с тремя вертикальными линиями внутри представляет процесс вертикальной сушки без отжима, при которой текстильное изделие сушится при подвешивании его мокрым с восстановлением или без восстановления первоначальной формы или выравнивания в помещении или вне его без удаления избытка воды (отжима).
Квадрат с одной горизонтальной линией внутри представляет процесс горизонтальной сушки на плоскости в расправленном состоянии, при котором текстильному изделию придают первоначальную форму и сушат в горизонтальном положении на плоской поверхности в помещении или вне его после удаления избытка воды (отжима).
Квадрате двумя диагональными линиями в левом верхнем углу обозначает сушку без прямого солнечного освещения. Этот символ помещают над символами вертикальной сушки, вертикальной сушки без отжима и сушки на плоскости в расправленном состоянии, чтобы показать, что процесс естественной сушки следует проводить в тени.
|
Таблица С.1 — Символы для процесса естественной сушки | ||||||||||
|
ГОСТ Р ИСО 3758-2007
Методы испытаний для определения или подтверждения инструкций по уходу с применением естественной сушки описаны в ИСО 6330 —для вертикальной сушки (подраздел 8.1), вертикальной сушки без отжима (подраздел 8.2) и горизонтальной сушки на плоскости в расправленном состоянии (подраздел 8.3).
Приложение D (справочное)
Примеры дополнительных надписей
D.1 Определение
Дополнительная надпись является дополнительной информацией по уходу, которая может сопровождать символьную инструкцию по уходу и является необходимой для ухода за текстильными изделиями с целью предотвращения нанесения вреда изделию или другим вещам, чистящимся вместе с ним, позволяя обычное использование и обращение с текстильным изделием.
D.2 Примеры дополнительных надписей
Примеры обычно используемых дополнительных надписей:
- только профессиональная чистка кожи;
- без оптических отбеливателей;
- использовать стиральную сетку;
- не гладить с паром;
- только с паром;
- не замачивать;
- рекомендуется гладить с паром;
- сушить в удалении от источника тепла;
- расправить во влажном состоянии;
- вертикальная сушка;
- расправить и сушить на плоскости;
- вертикальная сушка без отжима;
- не сушить на солнце.
- удалить ... до стирки;
- стирать отдельно;
- стирать с вещами такой же окраски;
- стирать до использования;
- стирать вывернутым наизнанку;
- не скручивать или не крутить;
- только при увлажнении;
- не добавлять тканевый кондиционер;
- удалить сразу;
- гладить только с изнанки;
- не гладить отделку;
- использовать салфетку для пресса;
- сушить на плоскости;
Может быть необходимым использование других дополнительных слов, когда какая-либо часть описанной стандартной процедуры ухода, которую потребитель или сотрудник профессиональной химчистки мог бы предположить подходящей для использования, повредила бы изделие или другие изделия, чистящиеся вместе с ним. Число дополнительных слов в маркировке должно быть сведено к минимуму.
Приложение Е (справочное)
Сведения о соответствии национальных стандартов Российской Федерации ссылочным
международным стандартам
|
Таблица Е.1 | ||||||||||||
|
|
Обозначение ссылочного международного стандарта |
Обозначение и наименование соответствующего национального стандарта |
|
ИСО 105-С09:2001 |
* |
|
ИСО 105-D01:1993 |
ГОСТР ИСО 105-D01—99 Материалы текстильные. Определение устойчивости окраски. Часть D01. Метод определения устойчивости окраски к действию химической ЧИСТКИ |
|
ИСО 105-Е01:1993 |
* |
|
ИСО 105-1401:1993 |
* |
|
ИСО 105-Х11:1994 |
* |
|
ИСО 105-Х12:1994 |
* |
|
ИСО 2411:2000 |
* |
|
ИСО 3175-1:1998 |
* |
|
ИСО 3175-2:1998 |
* |
|
ИСО 3175-3:2003 |
* |
|
ИСО 3175-4:2003 |
* |
|
ИСО 3759:2006 |
ГОСТ Р ИСО 3759-2007 Изделия текстильные. Подготовка образцов материалов и одежды для проведения испытаний по определению изменений размеров |
|
ИСО 5077:2006 |
ГОСТ Р ИСО 5077-2007 Материалы текстильные. Метод определения изменений размеров после стирки и сушки |
|
ИСО 6330:2000 |
* |
|
ИСО 7768:2006 |
* |
|
ИСО 7769:2006 |
* |
|
ИСО 7770:2006 |
* |
|
ИСО 12945-1:2000 |
* |
|
ИСО 12945-2:2000 |
* |
|
ИСО 12945-4:1998 |
* |
|
ИСО 13936-1:2004 |
* |
|
ИСО 13936-2:2004 |
* |
|
ИСО 15487:1999 |
* |
|
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать | |
|
перевод на русский язык данного международного стандарта. Перевод данного международного стандарта на- | |
|
ходится в Федеральном информационном фонде технических регламентов и стандартов. | |
УДК 677.06:003.62:006.354 ОКС 59.080.30 М09
Ключевые слова: одежда, символы по уходу, стирка, сухая чистка, отбеливание, машинная стирка, ручная стирка, режимы чистки, режимы глажения, режимы стирки
Редактор Л.В. Коретникова Технический редактор В.Н. Прусакова Корректор Е.М. Капустина Компьютерная верстка А.Н. Золотаревой
Сдано в набор 11.09.2007. Подписано в печать 01.10.2007. Формат 60 х 84^. Бумага офсетная. Гарнитура Ариал. Печать офсетная. Уел. печ. л. 2,32. Уч.-изд. л. 1,50. Тираж 300 экз. Зак. 735.
ФГУП «СТАНДАРТИНФОРМ», 123995 Москва, Гранатный пер., 4. www.gostinfo.ru info@gostinfo.ru
Набрано во ФГУП «СТАНДАРТИНФОРМ» на ПЭВМ.
Отпечатано в филиале ФГУП «СТАНДАРТИНФОРМ» — тип. «Московский печатник», 105062 Москва, Лялин пер., 6.
ГОСТ Р ИСО 3758-2007
Содержание
1 Область применения...................................................1
2 Термины и определения................................................1
3 Изображение и значение символов..........................................2
4 Нанесение и применение символов.........................................7
Приложение А (справочное) Характеристики и доступные методы испытаний для правильного выбора
символов по уходу............................................8
Приложение В (справочное) Региональная и национальная практика маркирования символами
по уходу.................................................11
Приложение С (справочное) Символы для естественной сушки........................14
Приложение D (справочное) Примеры дополнительных надписей......................15
Приложение Е (справочное) Сведения о соответствии национальных стандартов Российской
Федерации ссылочным международным стандартам.....................15
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИЗДЕЛИЯ ТЕКСТИЛЬНЫЕ
Маркировка символами по уходу
Textiles. Care labelling code using symbols
Дата введения — 2008—07—01
1 Область применения
Настоящий стандарт
- устанавливает систему графических символов, предназначенных для использования при маркировке текстильных изделий (см. 4.1), несущих информацию, предупреждающую необратимое повреждение в процессе ухода за текстилем;
- определяет использование этих символов при маркировке.
В настоящем стандарте охвачены следующие виды домашней обработки: стирка, отбеливание, глажение и сушка после стирки. Включены также виды профессиональной обработки — сухая и мокрая чистки; исключено промышленное глажение. Настоящий стандарт применим ко всем текстильным изделиям в том виде, в каком они поставлены потребителю.
2 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1 текстильные изделия: Пряжа (нити), метражные текстильные материалы и готовые изделия, содержащие текстильные материалы не менее 80 % от массы.
2.2 стирка: Процесс, предназначенный для очистки текстильных изделий в водной среде.
Примечание — Стирка включает все или некоторые изследующихопераций в необходимых сочетаниях:
- замачивание, предварительная и основная стирка, проводимые обычно при нагревании, механическом воздействии и при наличии моющих средств или других продуктов, и полоскание;
- отжим, т.е. выкручивание или выжимание, выполняемый во время и/или в конце упомянутых выше операций.
Эти операции могут быть выполнены машинным или ручным способом.
2.3 отбеливание: Процесс, происходящий в водной среде до, в течение или после стирки, требующий использования окисляющего средства, включающего либо хлорсодержащие или кислородсодержащие (без хлора) вещества, применяющегося с целью улучшения удаления грязи и ржавчины и/или придания большей белизны.
2.3.1 хлорный отбеливатель: Средство, которое выделяет в раствор ионы гипохлорита, например гипохлорит натрия.
2.3.2 кислородный/бесхлорный отбеливатель: Средство, которое выделяет в раствор пере-кисные соединения.
Издание официальное
Примечание — Отбеливающие кислородные средства включают широкий спектр различных активированных и неактивированных отбеливающих веществ, которые отличаются по своей активности.
2.3.3 активатор отбеливания: Средство, которое позволяет проводить отбеливание при более низких температурах.
2.4 сушка: Процесс, проводимый с текстильными изделиями после стирки, чтобы устранить излишнюю воду (или влагу).
2.4.1 барабанная сушка после стирки: Процесс, проводимый с текстильными изделиями после стирки, направленный на удаление остаточной воды путем обработки горячим воздухом во вращающемся барабане.
2.4.2 естественная сушка: Процесс, проводимый с текстильными изделиями после стирки, предназначенный для удаления остаточной воды путем сушки на веревке или планке, сушки стекания, сушки на солнце или в тени.
2.5 глажение и прессование: Процесс, проводимый с текстильным изделием для восстановления его формы и внешнего вида с помощью подходящего приспособления, использующего нагревание, давление и, возможно, пар.
2.6 профессиональный уход за текстилем: Профессиональные сухая и мокрая чистки, исключая коммерческую стирку.
2.6.1 профессиональная сухая чистка: Процесс чистки изделий из текстиля путем обработки в каком-либо растворителе (за исключением воды), обычно используемом для сухой чистки профессионалами.
Примечание — Этот процесс состоит из чистки, полоскания и центрифугирования. За ними следует проводимая подходящим методом сушка и восстановительные отделочные процедуры.
2.6.2 профессиональная мокрая чистка: Процесс чистки текстильных изделий в воде, проводимый профессионалами при использовании специальной технологии (чистки, полоскания и центрифугирования), моющих средств и добавок, минимизирующих неблагоприятные последствия.
Примечание — Процесс завершается подходящей сушкой и восстановительными отделочными процедурами.
3 Изображение и значение символов
3.1 Основные и дополнительные символы
Устанавливают пять основных символов и четыре дополнительных.
3.1.1 Стирка
|
г п |
|
L J Рисунок 1 |
Процессы стирки обозначают изображением таза с жидкостью, как показано на рисунке 1.
3.1.2 Отбеливание
|
Рисунок 2 |
Процессы отбеливания обозначают изображением треугольника, как показано на рисунке 2.
2
ГОСТ Р ИСО 3758-2007
3.1.3 Сушка
Процессы сушки обозначают изображением квадрата, как показано на рисунке 3.
|
Рисунок 3 |
3.1.3.1 Сушку в барабанной сушилке после процесса стирки обозначают квадратом с вписанной в него окружностью, как показано на рисунке 4.
Г ~1
L J
Рисунок 4
3.1.3.2 Дополнительная информация о символах естественной сушки приведена в приложении С.
3.1.4 Глажение и прессование
Процессы глажения и прессования обозначают изображением ручного утюга, как показано на рисунке 5.
г п
|_ j
Рисунок 5
3.1.5 Профессиональный уход за текстилем
Профессиональную сухую чистку и профессиональную мокрую чистку (за исключением коммерческой стирки) обозначают изображением окружности, как показано на рисунке 6.
|
Рисунок 6 |
3.1.6 Обработка запрещена
В дополнение к шести символам, описанным в 3.1.1 — 3.1.5, изображение креста на любом из них означает, что обработка, обозначенная этим символом, запрещена.
г п
X
|_ _|
Рисунок 7
з
3.1.7 Мягкая (умеренная) обработка
В дополнение к основным символам черта под символом означает, что обработка должна быть мягче (умереннее), чем предусмотрено этими символами без черты под ними, например, менее интенсивное перемешивание.
г п
L J
Рисунок 8
3.1.8 Очень мягкая обработка
В дополнение косновным символам двойная черта под символом характеризует очень мягкий процесс, например, очень слабое перемешивание.
г п
L J
Рисунок 9
3.1.9 Температура обработки
Температуру, связанную с символом 3.1.1, указывают в виде цифры, обозначающей градусы Цельсия (30,40, 50, 60, 70 или 95) без значка «°С».
В дополнение к трем символам 3.1.1 (стирка), 3.1.3 (сушка) и 3.1.4 (глажение и прессование) для определения температурного воздействия обработки могут быть использованы точки (от одной до шести). Указание температуры приводят совместно с символами основных обработок.
г “I г “I г п
• • • • • •
1_ J , L J , L J
Рисунок 10
3.2 Стирка
Таз обозначает домашнюю стирку (ручную или машинную) (см. рисунок 1). Этот символ используется для сообщения информации, касающейся максимальной температуры стирки и режима стирки в соответствии с таблицей 1.
|
Таблица 1 — Символы для режима стирки | ||||||||||
| ||||||||||
|
4 |
|
Окончание таблицы 1 | ||||||||||||||||||||||||
|
3.3 Отбеливание
Треугольник обозначает процесс отбеливания (см. рисунок 2 и таблицу 2).
|
Таблица 2 — Символы для отбеливания | ||||||||
|
3.4 Сушка
3.4.1 Естественная сушка
Естественная сушка описана в приложении С.
3.4.2 Барабанная сушка
Окружность, вписанная в квадрат, обозначает сушку в барабане (см. рисунок 4). Установленные максимальные температуры указывают одной или двумя точками внутри этого символа (см. таблицу 3).
Таблица 3 — Символы для барабанной сушки
Символ
Режим барабанной сушки
Возможна барабанная сушка; обычная температура
Возможна барабанная сушка; сушка при более низкой температуре
Не применять сушку в барабане
3.5 Глажение и прессование
Утюг обозначает домашний процесс глажения и прессования с использованием и без использования пара (см. рисунок 5). Максимальные уровни температуры указываются одной, двумя и тремя точками, расположенными внутри символа, как показано в таблице 4.
|
Таблица 4 — Символы для глажения | ||||||||||
|
3.6 Профессиональный уход за текстилем
Окружность (см. рисунок 6) обозначает процессы сухой и мокрой чистки текстильных изделий (исключая натуральную кожу и меха), проводимые профессионалами. Эти символы дают информацию относительно различных режимов чистки, указанных в таблице 5. Использование символа мокрой чистки не обязательно.
|
Таблица 5 — Символы для профессионального ухода за текстилем | ||||||||||
|