ГОСТ Р ИСО 24153-2012
Статистические методы. Процедуры рандомизации и отбора случайной выборки
Устанавливает процедуры рандомизации и случайного отбора выборки. Представленные в стандарте процедуры охватывают методы, предусматривающие применение технических средств, таблиц случайных чисел, компьютерных программ. Для компьютерных программ приведены общее описание соответствующего алгоритма и текст программы. В стандарте представлены не все возможные способы применения процедур случайного отбора выборки и рандомизации и не все возможные стратегии отбора выборки и определения объема выборки. В соответствующих ситуациях следует использовать стандарты, перечисленные во введении.
Идентичен ISO 24153:2009
Оглавление
1 Область применения
2 Нормативные ссылки
3 Термины, определения и обозначения
4 Основные положения
5 Описание процедур случайного отбора выборки. Методы, использующие специальные устройства
6 Описание процедуры отбора псевдонезависимой случайной выборки. Метод таблицы
7 Описание процедуры отбора псевдонезависимой случайной выборки. Компьютерный метод
8 Применение к общим ситуациям отбора выборки
Приложение А (обязательное) Таблицы случайных чисел
Приложение В (справочное) Текст программы генерации случайных чисел
Приложение С (справочное) Текст программ для случайного отбора выборки и рандомизации
Приложение ДА (справочное) сведения о соответствии ссылочных международных стандартов ссылочным национальным стандартам Российской Федерации
Библиография
35 страниц
| Дата введения | 01.12.2013 |
|---|---|
| Добавлен в базу | 01.10.2014 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Строительство
- Раздел Экология
Организации:
| 29.11.2012 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 1272-ст |
|---|---|---|---|
| Разработан | АНО НИЦ КД |
Statistical methods. Randomization and random sampling procedures
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20
стр. 21
стр. 22

стр. 23

стр. 24

стр. 25

стр. 26

стр. 27

стр. 28

стр. 29

стр. 30
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
НАЦИОНАЛЬНЫЙ
СТАНДАРТ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ГОСТ Р исо 24153—2012
Статистические методыПРОЦЕДУРЫ РАНДОМИЗАЦИИ И ОТБОРА СЛУЧАЙНОЙ ВЫБОРКИ
ISO 24153:2009 Random sampling and randomization procedures (IDT)
Издание официальное
|
Москва Стандартинформ 2014 |
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией «Научно-исследовательский центр контроля и диагностики технических систем» (АНО «НИЦ КД») на основе собственного аутентичного перевода на русский язык международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК125 «Статистические методы в управлении качеством продукции»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 ноября 2012 г. № 1272-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 24153:2009 «Процедуры отбора случайной выборки и рандомизации» (ISO 24153:2009 «Random sampling and randomization procedures»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации и межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в ГОСТР 1.0-2012 (раздел 8). Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок—в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (gost.ru)
©Стандартинформ, 2014
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
Пример 3 — В условиях задачи, рассмотренной в примере 2, очевидно, что использование трех игральных костей позволяет получить числа от 1 до 63 = 216 (при объеме партии в 50 единиц). Контролер принимает решение фиксировать все результаты от 1 до 200, преобразуя их в числа из интервала от 1 до 50, и отбрасывать результаты более 200, чтобы избежать вероятностного искажения результатов. Четыре броска предыдущего примера в соответствии с этой схемой дают {3, 3,4},{6,1,3}, {5, 6, 6} и {2, 5, 5}, соответствующие числам 88, 183, 180 и 65. Из этих чисел произведено вычитание числа 50 столько раз, пока число не окажется в интервале от 1 до 50 (0 интерпретируют как N), что дает значения 38,33,30 и 15 соответственно. Таким образом, была получена выборка из 4 единиц, т. е. дальнейшие броски не нужны. Очевидно, что математически этот процесс эквивалентен применению уравнения v2 = 1 + (v1 - 1) mod N, где v1 — исходное значение, av2 — значение из интервала от 1 до N.
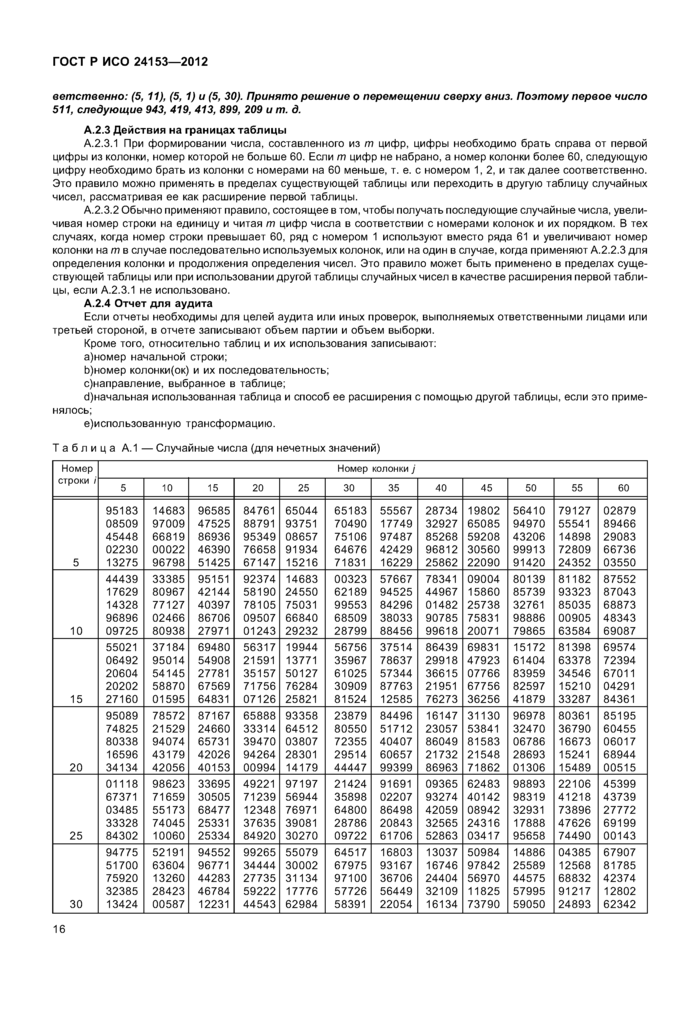
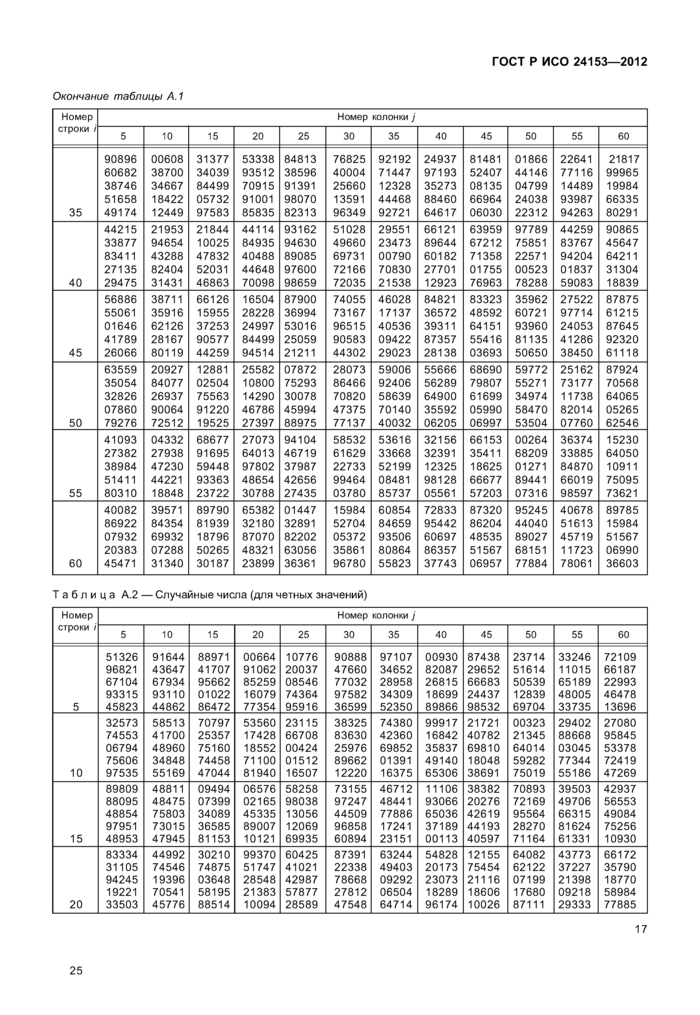
6 Описание процедуры отбора псевдонезависимой случайной выборки. Метод таблицы6.1 Таблицы случайных чисел
В приложении А приведены две таблицы случайных чисел. В каждой таблице приведено 3600 случайных чисел от 0 до 9, указанных в 60 строках по 60 колонок в каждой. Использование таблиц кратко описано ниже и более подробно в приложении А.
Примечание — Числа, приведенные в таблице, аналогичны значениям, выпадающим при бросании 10-гранного кубика. Количество цифр т, необходимых для отбора выборки, соответствует количеству бросков игральной кости.
6.2 Описание метода
6.2.1 Определяют количество цифр т, соответствующее объему партии N. Если объем партии является степенью 10, отбрасывают начальную цифру объема партии и интерпретируют оставшиеся нули при их появлении, как цифру, равную объему партии (например, если N = 1000, значение 000 при его появлении интерпретируют как 1000).
6.2.2 Случайным образом выбирают начальную точку (т. е. например, номер строки и колонки в таблице), используя метод, описанный в А.2.2.
6.2.3 Полученную цифру вместе с (т-1) цифрами справа от нее записывают как единое число. Если правее начальной цифры (до 60-ой колонки) недостаточно цифр для получения необходимого числа, используют колонки 1,2 и так далее вместо колонок 61,62 и так далее соответственно.
6.2.4 Увеличивают номер строки на единицу, повторяют 6.2.3 и записывают полученное значение. Если полученный номер строки превышает 60, в качестве следующей используют строку 1 и увеличивают номер каждой колонки на т.
6.2.5 Повторяют 6.2.4, отбрасывая все значения более N и, в случае отбора выборки без возвращения, все значения, которые были уже отобраны, пока необходимое количество выборочных единиц п не будет получено.
Пример — Контролеру необходимо отобрать случайную выборку объема 5 единиц из партии в 200 единиц. Случайной начальной точкой, определенной бросанием монеты, является число, расположенное в строке 57 и колонке 59 таблицы 1. Так как N много меньше максимального значения, которое можно получить на основе 3-х цифр (т. е. 1000), аудитор принимает решение использовать результаты из интервала от 1 до 1000, переводя их в интервал от 1 до 200. Получены следующие пять чисел: 848, 670, 902, 034 и 518. После перевода их в интервал от 1 до 200 получены значения 48, 70,102, 34 и 118.
7 Описание процедуры отбора псевдонезависимой случайной выборки. Компьютерный метод7.1 Краткий обзор
7.1.1 В настоящем стандарте использованы алгоритмы, приведенные в [1], [7] и [13]. Эти алгоритмы обладают математическими и статистическими свойствами, необходимыми для обеспечения случайного отбора выборки, создания программ на различных языках программирования и компьютерах, позволяющих проводить верификацию и ревизию отобранных значений, используемых для проверок, контроля, аудита. Текст основных элементов программы на языке программирования Си приведен в приложении В.
ГОСТ Р ИСО 24153-2012
7.1.2 В алгоритмах использованы два основных элемента:
a) алгоритм инициализации, генерирующий квазислучайное начальное целое число на основе времени, прошедшего с указанной даты;
b) генератор случайных чисел.
7.1.3 При использовании для верификации или аудита алгоритм инициализации, упомянутый в 7.1.2
а) и описанный в 7.2, может быть заменен введением начального значения вручную. Это значение должно быть целым числом из интервала от 1 до 2 147 483 398 включительно. Это значение необходимо сохранять и указывать в отчете (при составлении). Однако при использовании для контроля качества и при планировании эксперимента должна быть предусмотрена возможность не использовать компьютерный выбор начального значения, который может быть выбран по умолчанию.
Примечание — Этапы алгоритмов приведены в более формализованном виде, что может быть полезно при программировании методов. Текст программы со ссылками на подразделы настоящего стандарта приведен в приложении В.
7.2 Алгоритм инициализации
7.2.1 Алгоритм инициализации включает:
a) алгоритм вычисления времени, прошедшего с указанной даты;
b) алгоритм генерации случайных чисел на основе равномерного распределения, использующий случайное число, полученное на этапе а).
7.2.2 Приведенный алгоритм позволяет определить количество секунд с 2000-01-01 00:00:00 до текущих даты и времени.
Описание алгоритма.
a) Определяют системные дату и время компьютера в виде символьной переменной, сохраняют значение этой переменной и указывают в отчете, а затем анализируют переменную по компонентам (год, месяц, день, час, минута, секунда).
b) Вычисляют количество полных дней de, начиная с указанной даты, используя для текущей даты числовые значения года у (с четырьмя цифрами), месяца тл и дня d, обработанные следующим образом:
если л?1 < 3, то л?1 = л?1 + 12, у - у - 1,
de = d + L( 153/Т71 - 457)/5j + 365у + Ly/4j - Ly/100J + Ly/400j - 730 426.
Примечание — Формула для de может быть упрощена для календарных лет до 2099 года включительно заменой членов после Ly/4j на « -730 441».
c) Вычисляют общее количество секунд se, начиная с указанной даты, используя расчеты в соответствии с Ь) и время дня (в 24-часовом формате «hh:mm:ss»), указанное в символьной переменной в соответствии с а) на основе формулы
se = 86400de + 3600ft + 60m2 + s, где ft, m2 ns — часы, минуты и секунды соответственно.
Примечание 1 — В некоторых языках программирования есть встроенные функции для вычисления se непосредственно. Перед использованием такие встроенные функции должны быть проверены для обеспечения учета влияния високосных лет, летнего/зимнего времени (в зависимости от обстоятельств).
Примечание 2 — В 32-битовой реализации этого алгоритма значение se увеличивается до переполнения соответствующей ячейки. В программе необходимо предусмотреть проверки того, что это число находится в интервале от 1 до 2 147 483 398 включительно.
d) Значение, полученное в соответствии с с), является начальным числом для генератора начального числа и используется для получения заключительного начального числа. Это значение хранят в виде отдельной переменной и указывают в отчете.
e) Количество; обращений к генератору случайных чисел является случайным целым от 1 до 100, полученным на основе двух наименее существенных цифр значения, полученного в соответствии с перечислением с), увеличенного на 1, и может быть рассчитано по формуле
j = se- 100 Lse/100j + 1.
7.2.3 Алгоритм генерации начального числа (функция инициализации) представляет собой линейное конгруэнтное рекуррентное отношение.
7
Описание алгоритма (для компьютеров, способных обрабатывать 32-битовые целые числа).
a) х,+= 40692 х, mod 2 147 483 399;
b) к = Lx,/52774J;
c) х/ + 1 = 40692 (х, - 52774 к) - 3791 к)
d) если х,+1 < 0, то х/+1 = х/+1 + 2 147 483 399.
7.2.4 Генерируют начальное число алгоритма случайного отбора выборки, выбирая результат 7.2.2 с) в качестве х, и затем обращаясь к формуле 7.2.3 j раз (см. 7.2.2 е)), заменяя каждый раз х, на х,+1 до тех пор, пока не будет выполнено необходимое количество обращений.
7.2.5 Заключительное значение х,+1 на этапе 7.2.4 является случайным целым числом из интервала от 1 до 2 147 483 398 и может быть использовано как начальное число в алгоритме отбора выборки, описанном в 7.3 (в частности, как значение у, в 7.3.6 Ь)). Это значение сохраняют как отдельную переменную и указывают в отчете.
7.3 Алгоритм генерации случайных чисел
7.3.1 Алгоритм генерации случайных чисел включает
a) сохранение массива чисел, полученных с помощью алгоритма генерации равномерно распределенных случайных чисел;
b) перестановки чисел, полученных на основе алгоритма генерации равномерно распределенных случайных чисел.
7.3.2 Создают массив А из 32 элементов, который используют для сохранения выходных данных алгоритма случайного отбора выборки.
7.3.3 Для формирования массива А используют следующий генератор случайных чисел.
Описание алгоритма (для компьютеров, способных обрабатывать 32-битовые целые числа):
a) х,- + 1 = 40 014 х,- mod 2 147 483 563;
b) к = |_х,- / 53 668J;
c) х,+1 = 40 014 (х, - 53 668/с) - 12 2111с;
d) если х/+1 < 0, то х/+1 = хм + 2 147 483 563.
7.3.4 Инициализируют массив А, присваивая х,-результат 7.1.3 или 7.2.5, и затем обращаются к генератору в соответствии с 7.3.3 а) 40 раз, заменяя х,- на хм при каждом обращении, отбрасывая первые 8 значений, а затем присваивая каждое из оставшихся в массиве 32 значений х/+1 в обратном порядке (т. е. с 32-го элемента до 1-го элемента).
7.3.5 Выбирают первый элемент из массива А (т. е. А[1]) в качестве значения к, инициализирующего комбинированный алгоритм генерации случайных чисел.
7.3.6 Комбинированный генератор случайных чисел для генерации случайной выборки представляет собой комбинацию линейных конгруэнтных рекуррентных соотношений и определения индекса элемента массива А.
Описание алгоритма:
a) х,-+1 = 40 014 х,-mod 2 147 483 563;
b) у,+1 = 40 692 у,- mod 2 147 483 399;
c) J = L32 Аг/2 147 483 563J+ 1;
d) k = A[J] -y,+i;
e) A[J] = х,-+1;
f) если к< 1,70 к = к + 2 147 483 562.
7.3.7 Алгоритм в соответствии с 7.3.6 инициализируют путем присвоениях,-значения х,+1, полученного в соответствии с 7.3.4, и присвоения у, значения в соответствии с 7.2.5. Значения х,-+1 и у/+1 служат далее значениями х,- и у,- для всех последующих обращений к алгоритму. Случайный индекс J для элемента массива А вычисляют, используя значение к (см. 7.3.5), которому присваивают значение, равное разности (A[J] -y,-+i), a A[J] заменяют на х,- + 1. Наконец, при необходимости получения положительного значения, знак к меняют на противоположный.
ГОСТ Р ИСО 24153-2012
7.3.8 Входом алгоритма случайного отбора выборки является значение к, представляющее собой случайное число из интервала от 1 до 2 147 483 562, трансформированное в действительное равномерно распределенное случайное число U из интервала от 0 до 1 (исключая конечные точки этого интервала) следующим образом: U - к/2 147 483 563.
7.3.9 Выход 7.3.8 может быть представлен в виде случайного целого числа L, равномерно распределенного в интервале от 1 до N включительно, следующим образом:
l = In и} + 1.
7.3.10 Выполняют генерацию случайной выборки в соответствии с 7.3.6—7.3.9, повторяя эти действия до тех пор, пока не будет получено необходимое количество случайных чисел.
7.4 Отчет
Если отчет необходимо сохранять для аудита или других проверок установленных требований, необходимо записывать объем партий и объем выборки.
Кроме того, следует записывать значение начального числа, введенного вручную в соответствии с
7.1.3 или полученного с помощью случайного генератора начального числа.
В отчете также указывают:
a) системные дату и время компьютера, используемые для вычисления начального числа;
b) значение начального числа в 7.2.2 d);
c) заключительное значение в соответствии с 7.2.5.
8 Применение к общим ситуациям отбора выборки8.1 Общие положения
8.1.1 Ниже приведены алгоритмы для нескольких стратегий отбора случайной выборки в различных практических ситуациях.
8.1.2 В настоящем разделе U — случайная действительная переменная, равномерно распределенная в интервале от 0 до 1 за исключением значений в конечных точках интервала (см. 7.3). Если для определения U использован другой источник и известно, что полученные значения лежат в интервале, не включающем точку 0, принимают U = (1 - U). Если использованный источник значений U включает 0 и 1 (обе конечные точки интервала), значение 1 должно быть исключено.
8.2 Случайное целое из интервала
Приведенный алгоритм позволяет генерировать случайное целое К из интервала от М до N включительно.
Описание алгоритма.
a) Генерируют случайное действительное число U.
b) Вычисляют К- М + \_U {N- М + 1)_|.
8.3 Случайная перестановка
Приведенный алгоритм позволяет получить случайную перестановку из N единиц по л для массива Л с N различными элементами.
Описание алгоритма:
a) Формируют массив Л [1:А/], состоящий из N индексированных элементов, расположенных в исходном порядке.
b) Присваивают J значение 1.
c) Г енерируют случайное целое число К из интервала от J до N включительно.
d) Значения A[J] и Л [К] меняют местами.
e) Увеличивают J на 1.
f) Если J меньше или равно л, возвращаются к с).
д) Получена случайная перестановка из первых л значений массива Л.
8.4 Случайное изменение порядка
Приведенный алгоритм позволяет для массива Л из N различных элементов произвести случайное изменение порядка N элементов.
9
Описание алгоритма:
a) Формируют из N индексированных элементов в исходном порядке массив/\[1:Л/] и создают копию массива А[ 1 :Л/] в массиве В[ 1 :Л/].
b) Выполняют случайную перестановку N элементов из N (т. е. всех) массива 6[1 \N] в соответствии
с 8.3.
c) Сравнивают элементы с 1-годо N- го массивов А и В для выявления равных.
d) Если элемент массива В равен соответствующему элементу массива А, прекращают сравнение и переходят к выполнению Ь).
e) Получен массив В со случайным изменением порядка элементов массива А.
Примечание — Этот алгоритм может быть более эффективным при выполнении Ь) и с), если сравнение элементов A[J] и B[J] выполнять сразу после определения B[J], не дожидаясь полной перестановки набора В.
8.5 Случайный отбор с возвращением
Приведенный алгоритм позволяет произвести случайный отбор с возвращением единственной выборки из п единиц из партии объема N.
Описание алгоритма.
a) Генерируют случайное целое число К из интервала от 1 до N включительно.
b) Повторяют а) до тех пор, пока не будет получено п значений К.
Примечание — Этот метод может быть применен неоднократно для получения любого количества выборок любого объема. Если полученные значения единственной выборки не ранжированы, такая выборка может быть использована для последовательного выборочного контроля.
8.6 Случайная выборка без возвращения
Приведенный алгоритм позволяет произвести случайный отбор единственной выборки, состоящей из п различных единиц, из партии N единиц.
Описание алгоритма.
a) Метод 1.
1) Генерируют случайное целое число К из интервала от 1 до N включительно.
2) Проверяют, что это значение К не было ранее генерировано. Если это значение К не было ранее генерировано, его сохраняют, в противном случае — отбрасывают.
3) Повторяют 1) и 2) до тех пор, пока не будет получено п различных значений К.
b) Метод 2.
1) Выполняют случайную перестановку л единиц из N в соответствии с 8.3.
2) Используют первые п значений массива А в качестве случайной выборки.
Примечание — Каждый из этих методов может быть использован для получения любого количества выборок различного объема (для таких целей, как двухступенчатый или многоступенчатый контроль). При использовании общего количества п(- индивидуальных объемов выборки п( в качестве входного значения п алгоритма, генерирующего неупорядоченные данные, первые пл полученных значений являются первой выборкой, следующие п2 значений — второй выборкой и т. д. Кроме того, если полученные значения единственной выборки не ранжированы, то выборка может быть использована для последовательного выборочного контроля.
8.7 Случайный отбор выборки для планов непрерывного выборочного контроля (CSP1*)
План непрерывного выборочного контроля CSP-1 разработан для применения при контроле качества продукции производственной линии и представляет собой смену периодов сплошного и выборочного контроля (после / последовательно принятых единиц продукции сплошной контроль заменяют на выборочный контроль с долей отбора f, который снова заменяют на сплошной контроль после обнаружения несоответствующей единицы продукции). Ниже приведено описание двух методов, позволяющих отбирать продукцию для выборочного контроля.
Описание алгоритма.
а) Метод 1.
1) Для каждой единицы продукции генерируют случайное действительное значение U {U е [0,1]).
2) Если U меньше или равно f, соответствующую единицу выбирают для выборочного контроля.
О CSP — continuous sampling plans.
ГОСТ Р ИСО 24153-2012
3) Повторяют 1) и 2) до тех пор, пока не будет обнаружена несоответствующая единица продукции.
Ь) Метод 2.
1) Для каждой группы из л единиц продукции, где п = Mf, генерируют случайное целое число К из интервала от 1 до л включительно.
2) Выбирают единицу, соответствующую значению К, в качестве выборочной единицы для контроля.
3) Повторяют 1) и 2) до тех пор, пока не будет получена несоответствующая единица продукции. Примечани е —Для планов CSP-1 значение f устанавливают равным числу, обратному к целому числу.
8.8 Отбор расслоенной случайной выборки
Для партии, составленной из двух или более слоев объема Л/,-, отбирают единственную случайную выборку объема л,- из каждого /'-го слоя, используя методы, приведенные в 8.3 или 8.6, если необходим отбор выборки без возвращения, или метод, приведенный в 8.5, если необходим отбор с возвращением.
8.9 Отбор единственной случайной выборки из партии с первоначально неизвестным объемом
Приведенный алгоритм позволяет получить единственную случайную выборку, состоящую из л различных единиц, отобранную из партии, первоначальный объем которой неизвестен (но не менее л). Описание алгоритма (адаптированный метод из [11]):
a) Определяют первые л единиц в партии и формируют массив Л[1 :л].
b) Если в партии существует еще единица продукции, устанавливают N равным номеру следующей единицы, в противном случае переходят Kf).
c) Генерируют случайное целое число К из интервала от 1 до N включительно.
d) Если К> л, устанавливают А[К\ - N.
e) Переходят к выполнению Ь).
f) Получена случайная выборка объема л в массиве Л при объеме партии не менее N. Примечание — Данный метод может быть также использован, если объем партии известен.
8.10 Отбор единственной упорядоченной случайной выборки без возвращения
Приведенный алгоритм позволяет получить единственную случайную выборку л различных единиц из партии объема N, генерированную сразу в порядке возрастания.
Описание алгоритмов:
a) Метод 1 (адаптированный метод из [2]).
1) Инициализируют следующие переменные:
i) создают массив Л[1:л];
ii) устанавливают L = N, К = (N - п) и J = 0.
2) Увеличивают значение J на 1.
3) Если J>n, переходят к 8).
4) Генерируют случайное действительное число U и устанавливают Р = 1.
5) Устанавливают Р = Р ■ KIN.
6) Если P<U:
i) устанавливают A[J]=(N-L + 1) и уменьшаютL на 1;
ii) переходят к выполнению 2).
7) Если Р> U:
i) уменьшают L и К на 1;
ii) переходят к выполнению 5).
8) Получена случайная выборка из элементов, номера которых в массиве Л расположены в порядке возрастания.
b) Метод 2 (адаптированный метод из [3]).
1) Пусть С(а,Ь) — функция, равная числу сочетаний из а по b без повторений (также известная как биномиальный коэффициент и равная а!/[(а-Ь)! ■£>!]).
2) Г енерируют случайное целое число L из интервала от 1 до С (Л/, п) включительно.
3) Создают массив Л[1:л].
4) Устанавливают N=0^=^ и т - (п - 1).
11
5) Устанавливают A[J\ = 0.
6) Если иф 1, устанавливают A[J\ -A[J- 1].
7) Устанавливают A[J] = A[J] + 1.
8) Устанавливают R - C(N-A[J], n-J).
9) Увеличивают К на R.
10) Если К< L, переходят к выполнению 7).
11) Уменьшают К на R.
12) Увеличивают J на 1.
13) Если J< N, переходят к выполнению 5).
14) Устанавливают А[п] -А[т] + L- К.
15) Получена случайная выборка, расположенная в порядке возрастания номеров массива А.
Примечание — Вследствие ограничений компьютерного представления больших целых чисел, а также применения генераторов случайных чисел, необходимо проверить, что метод 2 в вычислительном отношении выполним, а генерируемые случайные числа не имеют чрезмерного смещения.
Пример — Необходимо получить упорядоченную случайную выборку объема 5 единиц из партии в 25 единиц. Существует 25!/(20!5!) = 53130 возможных комбинаций по 5 единиц из 25 единиц, что выполнимо при использовании современных компьютеров. Для этих целей выбран генератор случайных чисел, описанный в разделе 7, его максимальное значение 2 147 483 562 более чем в 40 419 раз больше, чем максимальное из требуемых чисел, таким образом, смещение метода является незначительным. Гене-рировано единственное случайное целое число (7319) из интервала от 1 до 53130. В результате получена выборка (1, 7, 13, 18, 19}.
8.11 Кластерный отбор
Для совокупности или партии, состоящей из кластеров единиц, составляют перечень кластеров и отбирают случайную выборку, используя методы, приведенные в 8.3 или 8.6, если необходим отбор без возвращения. Полученная выборка включает единицы всех кластеров.
8.12 Случайный отбор выборки из набора целых чисел с вероятностью отбора числа в выборку пропорциональной егозначению
Отбор, пропорциональный значению единиц, применяют к совокупности, состоящей из единиц, представляющих собой различные целые числа. Приведенный метод обеспечивает получение случайной выборки, отобранной таким образом, что вероятность отбора числа в выборку пропорциональна значению этого числа.
Описание алгоритмов.
a) Метод 1.
1) В списке из N единиц, расположенных в соответствии с возрастанием значений, последовательно указывают кумулятивные суммы S,, соответствующие каждой единице.
2) Генерируют случайное целое число К из интервала от 1 до SN включительно, где SN — общая кумулятивная сумма совокупности.
3) Из перечня отбирают в выборку единицу, которой соответствует наибольшее значение кумулятивной суммы, не превышающее К.
4) Повторяют 2) и 3) до тех пор, пока необходимое количество п единиц выборки (с возвращением или без возвращения) не будет получено.
b) Метод 2.
1) Из перечня N различных значений единиц совокупности определяют максимальное значение М.
2) Генерируют два случайных целых числа (К, L), К из интервала от 1 до N включительно, a L из интервала от 1 до М включительно.
3) Если значение К-й единицы не превышает/., выбираютК-ую единицу в качестве выборочной единицы.
4) Повторяют 2) и 3) до тех пор, пока не будет получено необходимое количество л выборочных единиц (с возвращением или без возвращения).
Пример — Маркетинговая компания намерена провести отбор домашних хозяйств с выбором, пропорциональным количеству членов семьи в хозяйстве. Число членов семьи десяти домашних хозяйств в порядке возрастания: 2,2,3,3,3,4,4,5, 6, 7. Соответствующее кумулятивное число членов семьи: 2,4, 7,
10,13,17,21,26,32,39. Необходимо получить случайную выборку из 4 домашних хозяйств без возвращения. Генерировано 4 случайных целых числа от 1 до 39, {7,33,2,11}. Соответствующие единицы выборки — это хозяйства, указанные в списке под номерами {3, 9,1,4}.
8.13 Многостадийный отбор
Для совокупности или партии с иерархической структурой выбирают случайную выборку из больших групп, затем делают подвыборку меньших групп из каждой ранее отобранной группы, продолжая эту процедуру до тех пор, пока не будет достигнут уровень единицы. На каждой стадии используют методы случайного отбора выборки, приведенные в 8.3 или 8.6, если необходима выборка без возвращения, или метод, приведенный в 8.5, если необходим отбор с возвращением. Количество единиц в итоговой выборке равно произведению объемов выборки на каждой стадии.
Пример—Партия состоит из 20 поддонов с 20 ящиками на каждом поддоне. Каждый ящик содержит 10 единиц продукции. Покупатель намерен проверить продукцию, используя стратегию многостадийного отбора. Отобрана случайная выборка из 4 поддонов. С каждого отобранного поддона отобрана случайная выборка из 4-х ящиков. Наконец, из каждого отобранного ящика отобрана случайная выборка из 3 единиц. Эта процедура обеспечивает получение выборки из 48 единиц продукции из партии в 4000единиц.
8.14 Рандомизация при планировании эксперимента
При использовании планирования экспериментов рандомизацию применяют для выполнения таких действий, как назначение экспериментальной обработки исследуемых единиц или объектов и установление порядка их оценки, включая порядок оценки при повторении эксперимента. При этом может быть использован любой из приведенных методов рандомизации.
Описание алгоритмов.
a) Метод 1.
1) Для каждого элемента из перечня А/обработок или единиц (в зависимости от обстоятельств) назначают различные целые числа от 1 до N.
2) Выполняют случайную перестановку N целых чисел из N (т. е. всех).
3) Выполняют экспериментальные действия в последовательности, соответствующей порядку, определенному в 2).
b) Метод 2.
1) Генерируют N случайных действительных чисел I/, и присваивают их значения в порядке следования соответствующим элементам перечня обработок или единиц (в зависимости от обстоятельств).
2) Сортируют элементы перечня обработок или единиц в порядке возрастания соответствующих им
значений и,.
3) Выполняют экспериментальную деятельность в соответствии с полученной последовательностью (см. 2).
Пример 1 — В процессе медицинских исследований необходимо проверить воздействие нового препарата по сравнению с обычно используемым препаратом в конкретной медицинской ситуации. В клинических испытаниях участвуют двенадцать добровольцев, каждому из которых присваивают номер от 1 до 12. Исследователь планирует применить препарат А (новый препарат) к 6 субъектам, а препарат В (обычно применяемый препарат) к другим 6 субъектам. Для уменьшения смещения экспериментатор принимает решение сначала рандомизировать порядок планируемых 12 применений препаратов, а затем распределить их между 12 добровольцами. Индексы препаратов и испытуемых субъектов рандомизируют каждый отдельно, используя метод 1. Полученные рандомизированные перечни препаратов {В, В, А, В, А, А, В, А, А, В, В, А} и испытуемых {3, 7, 12, 5, 1, 9, 11, 4, 10, 2, 8, 6}. Препараты теперь могут быть назначены соответствующим испытуемым на основе перечня {ВЗ, В7, А12, В5, А1, А9, В11, А4, А10, В2, В8, А6}. Следовательно, препарат А должен быть применен для субъектов {1,4, 6, 9,10,12}, а препарат В — для субъектов {2, 3, 5, 7, 8,11}.
Пример 2 — Экспериментатору необходимо провести повторный эксперимент, проверяя каждую из 5 единиц три раза, в случайном порядке. Случайная перестановка набора {1, 2,3,4,5} дала три набора: {2,1,5,4,3}, {1,5,2,3,4}, и {4,3,5,2,1}.Этим трем наборам присваивают номера (1,2иЗ) соответственно, а экспериментатор выполняет проверки единиц в соответствии с номером проверки и в порядке, соответствующем набору с этим номером.
8.15 Случайный латинский квадрат
Латинский квадрат порядка п представляет собой матрицу п х п, содержащую символы некоторого алфавита, расположенные так, что каждый символ появляется в каждой строке и в каждом столбце только
13
один раз. Латинский квадрат используют при планировании экспериментов. Приведенный алгоритм позволяет получить случайный латинский квадрат порядка п (см. [4]).
Описание алгоритма.
a) Создают массивы А[ 1 :п, 1 :п] и С[1 :п].
b) Устанавливают R - 1.
c) Вводят целые числа от 1 до л в массив С[1 :л].
d) Устанавливают J - N.
e) Устанавливают С = 1.
f) Устанавливают / = 0.
д) Генерируют случайное целое числоХв интервале от 1 до J включительно.
h) Устанавливают Н- 1.
i) Если / > 50, переходят к выполнению с).
j) Если А[Н, С] = С[Х], увеличивают значение / на 1 и переходят к выполнению д).
k) Увеличивают значение Н на 1.
l) Если H<(R~ 1), переходят к выполнению i).
m) Устанавливают A[R, С] = С[Х\ и уменьшают значение J на 1.
п) Если Х> J, переходят к выполнению г),
о) Устанавливают К-Х.
р) Устанавливают С[К] = С[К + 1].
q) Увеличивают К на 1; если K<J, переходят к выполнению р). г) Увеличивают С на 1; если С<п, переходят к выполнению f).
s) Увеличивают R на 1; если R < п, переходят к выполнению с).
t) В массиве Л получают случайный латинский квадрат.
Примечание — Алгоритм генерации равномерно распределенных случайных латинских квадратов приведен в [5]. В дополнение необходимо отметить, что имеется связь между случайным латинским квадратом и генерацией случайных перестановок отдельных строк и колонок латинского квадрата и перестановок всех предыдущих строк и колонок.
14
ГОСТ Р ИСО 24153-2012
Приложение А (обязательное)
Таблицы случайных чисел
А.1 Описание
В данном приложении приведены две таблицы случайных чисел, которые могут быть использованы в тех случаях, когда невозможно применение компьютерных алгоритмов генерации случайных чисел. В каждой таблице приведено 3600 случайных чисел от 0 до 9, каждое из которых появляется с равной частотой. Каждая таблица состоит из 60 строк по 60 колонок в строке, что облегчает использование текущего времени суток для установки начальной точки. Таблицы получены с использованием алгоритмов, описанных в разделе 7.
А.2 Использование
А.2.1 Количество знаков и интерпретация
А.2.1.1 Определяют количество знаков (цифр числа) т, необходимых для представления объема партии N. Количество знаков равно количеству знаков в объеме партии, за исключением ситуации, когда объем партии является степенью 10. В этом случае число, состоящее из нулей, количество которых равно количеству нулей в объеме партии, следует интерпретировать как число, равное объему партии (например, если N = 100, значение 00, при появлении, интерпретируют как 100).
А.2.1.2 Если объем партии меньше или равен половине 10т, начальное значение для использования таблицы может быть определено на основе трансформации наблюдаемого значения в интервале от 1 до N при условии, что в процесс не введено смещение. Этого легко достичь, отбрасывая все значения, превышающие kN, где к = Li 0m//\/J , до трансформации в соответствии с уравнением v2 = 1 + (v1 -1) mod А/, где v1 — начальное значение, v2 — значение из заданного интервала.
А.2.2 Начальная точка
А.2.2.1 До применения таблиц случайных чисел необходимо определить стратегию выбора начальной точки. Таблицы разработаны так, что позволяют использовать для выбора начальной точки показания часов, в том числе часов, показывающих время с точностью до секунды. Приведенный алгоритм реализует применение метода основанного на использовании показаний часов для выбора начальной точки.
Описание алгоритма:
a) Делают запись текущего времени в формате «час: мин: сек».
b) Используют значение секунд для определения номера строки, интерпретируя 00 как 60.
c) Используют значение минут для определения номера колонки, интерпретируя 00 как 60.
d) Используют показания часов для определения номера таблицы (А.1 или А.2) в зависимости от четного или нечетного часа.
Пример — Экспериментатору необходимо выбрать начальную точку в таблицах для отбора случайной выборки из партии в 100 единиц. Текущее время 10:35:13. Таким образом, начальная точка находится в таблице А.2. (т. к. 10— четное число) в 13-й строке, 35-й колонке. Здесь расположена цифра 6, но т. к. для отбора выборки из 100 единиц необходимы две цифры, использована цифра из колонки 36, таким образом, первая единица выборки имеет номер 66.
А.2.2.2 Может быть использован любой другой метод, обеспечивающий получение случайных равномерно распределенных целых чисел из интервала от 1 до 60 включительно, такой, как метод монеты или кубика (см. 5.2) или компьютерный алгоритм (см. раздел 7), позволяющий получить длинный список случайных координат начального числа, которые могут быть использованы в последующих случаях. Кроме того, в конце отбора выборки из таблицы в конкретном случае координаты начальной точки могут быть зарегистрированы и затем использованы как начальная точка для следующего отбора выборки.
Пример — В качестве продолжения примера А.2.2.1, предположим, что необходим случайный отбор 10 единиц. Получена выборка {66, 13, 10, 45, 32, 22, 41, 49, 22, 99}. Координаты следующего значения — строка 23 и колонка 35 (число 10). Эти значения могут быть зарегистрированы и использованы как начальная точка для следующего отбора выборки при необходимости.
А.2.2.3 Координаты исходной точки также могут быть определены путем установления начальной цифры на основе номеров ряда и колонки в соответствии с А.2.2.1 или А.2.2.2 и дополнительных цифр на основе номера текущей строки и дополнительных номеров колонок, основанных на случайных числах, генерированных без возвращения из интервала от 1 до 60 включительно для оставшихся (т - 1)-го знаков. Полученное многозначное число должно быть сформировано в том же порядке, в каком были генерированы номера колонок.
Пример — Необходима случайная выборка из партии в 1000 единиц. Начальные строка и колонка определены как 5 и 11 соответственно в таблице А. 1. Необходимы еще две цифры, и они бьти сгенерированы как 1 и 30. В результате получены следующие координаты первой, второй и третьей цифр соот-
15
Содержание
1 Область применения....................................... 1
2 Нормативные ссылки....................................... 1
3 Термины, определения и обозначения.............................. 2
4 Основные положения ...................................... 4
5 Описание процедур случайного отбора выборки. Методы, использующие специальные устройства 5
6 Описание процедуры отбора псевдонезависимой случайной выборки. Метод таблицы....... 6
7 Описание процедуры отбора псевдонезависимой случайной выборки. Компьютерный метод .... 6
8 Применение к общим ситуациям отбора выборки.......................... 9
Приложение А (обязательное) Таблицы случайных чисел....................... 15
Приложение В (справочное) Текст программы генерации случайных чисел.............. 19
Приложение С (справочное) Текст программ для случайного отбора выборки и рандомизации .... 22
Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов ссылочным национальным стандартам Российской Федерации.............. 28
Библиография............................................ 29
ветственно: (5, 11), (5, 1) и (5, 30). Принято решение о перемещении сверху вниз. Поэтому первое число 511, следующие 943, 419, 413, 899, 209 и т. д.
А.2.3 Действия на границах таблицы
А.2.3.1 При формировании числа, составленного из т цифр, цифры необходимо брать справа от первой цифры из колонки, номер которой не больше 60. Если т цифр не набрано, а номер колонки более 60, следующую цифру необходимо брать из колонки с номерами на 60 меньше, т. е. с номером 1, 2, и так далее соответственно. Это правило можно применять в пределах существующей таблицы или переходить в другую таблицу случайных чисел, рассматривая ее как расширение первой таблицы.
А.2.3.2 Обычно применяют правило, состоящее в том, чтобы получать последующие случайные числа, увеличивая номер строки на единицу и читая т цифр числа в соответствии с номерами колонок и их порядком. В тех случаях, когда номер строки превышает 60, ряд с номером 1 используют вместо ряда 61 и увеличивают номер колонки на т в случае последовательно используемых колонок, или на один в случае, когда применяют А.2.2.3 для определения колонки и продолжения определения чисел. Это правило может быть применено в пределах существующей таблицы или при использовании другой таблицы случайных чисел в качестве расширения первой таблицы, если А.2.3.1 не использовано.
А.2.4 Отчет для аудита
Если отчеты необходимы для целей аудита или иных проверок, выполняемых ответственными лицами или третьей стороной, в отчете записывают объем партии и объем выборки.
Кроме того, относительно таблиц и их использования записывают:
a) номер начальной строки;
b) номер колонки(ок) и их последовательность;
c) направление, выбранное в таблице;
(^начальная использованная таблица и способ ее расширения с помощью другой таблицы, если это применялось;
е)использованную трансформацию.
Таблица А.1 — Случайные числа (для нечетных значений)
|
Номер |
Номер колонки j | |||||||||||
|
строки / |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
|
95183 |
14683 |
96585 |
84761 |
65044 |
65183 |
55567 |
28734 |
19802 |
56410 |
79127 |
02879 | |
|
08509 |
97009 |
47525 |
88791 |
93751 |
70490 |
17749 |
32927 |
65085 |
94970 |
55541 |
89466 | |
|
45448 |
66819 |
86936 |
95349 |
08657 |
75106 |
97487 |
85268 |
59208 |
43206 |
14898 |
29083 | |
|
02230 |
00022 |
46390 |
76658 |
91934 |
64676 |
42429 |
96812 |
30560 |
99913 |
72809 |
66736 | |
|
5 |
13275 |
96798 |
51425 |
67147 |
15216 |
71831 |
16229 |
25862 |
22090 |
91420 |
24352 |
03550 |
|
44439 |
33385 |
95151 |
92374 |
14683 |
00323 |
57667 |
78341 |
09004 |
80139 |
81182 |
87552 | |
|
17629 |
80967 |
42144 |
58190 |
24550 |
62189 |
94525 |
44967 |
15860 |
85739 |
93323 |
87043 | |
|
14328 |
77127 |
40397 |
78105 |
75031 |
99553 |
84296 |
01482 |
25738 |
32761 |
85035 |
68873 | |
|
96896 |
02466 |
86706 |
09507 |
66840 |
68509 |
38033 |
90785 |
75831 |
98886 |
00905 |
48343 | |
|
10 |
09725 |
80938 |
27971 |
01243 |
29232 |
28799 |
88456 |
99618 |
20071 |
79865 |
63584 |
69087 |
|
55021 |
37184 |
69480 |
56317 |
19944 |
56756 |
37514 |
86439 |
69831 |
15172 |
81398 |
69574 | |
|
06492 |
95014 |
54908 |
21591 |
13771 |
35967 |
78637 |
29918 |
47923 |
61404 |
63378 |
72394 | |
|
20604 |
54145 |
27781 |
35157 |
50127 |
61025 |
57344 |
36615 |
07766 |
83959 |
34546 |
67011 | |
|
20202 |
58870 |
67569 |
71756 |
76284 |
30909 |
87763 |
21951 |
67756 |
82597 |
15210 |
04291 | |
|
15 |
27160 |
01595 |
64831 |
07126 |
25821 |
81524 |
12585 |
76273 |
36256 |
41879 |
33287 |
84361 |
|
95089 |
78572 |
87167 |
65888 |
93358 |
23879 |
84496 |
16147 |
31130 |
96978 |
80361 |
85195 | |
|
74825 |
21529 |
24660 |
33314 |
64512 |
80550 |
51712 |
23057 |
53841 |
32470 |
36790 |
60455 | |
|
80338 |
94074 |
65731 |
39470 |
03807 |
72355 |
40407 |
86049 |
81583 |
06786 |
16673 |
06017 | |
|
16596 |
43179 |
42026 |
94264 |
28301 |
29514 |
60657 |
21732 |
21548 |
28693 |
15241 |
68944 | |
|
20 |
34134 |
42056 |
40153 |
00994 |
14179 |
44447 |
99399 |
86963 |
71862 |
01306 |
15489 |
00515 |
|
01118 |
98623 |
33695 |
49221 |
97197 |
21424 |
91691 |
09365 |
62483 |
98893 |
22106 |
45399 | |
|
67371 |
71659 |
30505 |
71239 |
56944 |
35898 |
02207 |
93274 |
40142 |
98319 |
41218 |
43739 | |
|
03485 |
55173 |
68477 |
12348 |
76971 |
64800 |
86498 |
42059 |
08942 |
32931 |
73896 |
27772 | |
|
33328 |
74045 |
25331 |
37635 |
39081 |
28786 |
20843 |
32565 |
24316 |
17888 |
47626 |
69199 | |
|
25 |
84302 |
10060 |
25334 |
84920 |
30270 |
09722 |
61706 |
52863 |
03417 |
95658 |
74490 |
00143 |
|
94775 |
52191 |
94552 |
99265 |
55079 |
64517 |
16803 |
13037 |
50984 |
14886 |
04385 |
67907 | |
|
51700 |
63604 |
96771 |
34444 |
30002 |
67975 |
93167 |
16746 |
97842 |
25589 |
12568 |
81785 | |
|
75920 |
13260 |
44283 |
27735 |
31134 |
97100 |
36706 |
24404 |
56970 |
44575 |
68832 |
42374 | |
|
32385 |
28423 |
46784 |
59222 |
17776 |
57726 |
56449 |
32109 |
11825 |
57995 |
91217 |
12802 | |
|
30 |
13424 |
00587 |
12231 |
44543 |
62984 |
58391 |
22054 |
16134 |
73790 |
59050 |
24893 |
62342 |
Введение
Случайный отбор выборки и процедуры рандомизации являются основой многих статистических методов, используемых при проведении экспериментов, контроле качества продукции, совершенствовании и планировании экспериментов в медицине, биологии, сельском хозяйстве и ряда научных областей. Многие стандарты на статистические методы связаны с выполнением экспериментов. В частности, все перечисленные в таблице стандарты по статистическому приемочному контролю основаны на предположении, что для отбора необходимого количества единиц продукции использован случайный отбор выборки.
|
Таблица — Перечень международных и соответствующих им национальных стандартов РФ по статистическому приемочному контролю | ||||||||||||||||||||
|
ГОСТ Р ИСО 24153-2012
|
Окончание таблицы | ||||||||||||||
|
Кроме того, в стандартах ИСО 2859-3 и ИСО 21247 приведены условия применения случайного отбора выборки при определении возможности использования методов контроля с пропуском партии, а также для отбора единиц продукции при применении планов непрерывного выборочного контроля. Таким образом, очень важно до применения всех перечисленных стандартов обеспечить случайный отбор выборки.
Несмотря на то, что принципы настоящего стандарта универсальны и могут быть применены во всех ситуациях, где требуется случайный отбор выборки, а выборочные единицы могут быть четко определены (в виде дискретных единиц продукции), существует много ситуаций, в которых исследуемый материал не может быть предоставлен в виде дискретных единиц продукции. В таких ситуациях следует применять стандарты серии ИСО 11648 «Статистические аспекты выборочного контроля нештучной продукции»1* (все части).
Приведенные в настоящем стандарте процедуры рандомизации прошли проверку на соответствие заявленным свойствам, т. е. на соответствие указанному закону распределения с большим циклом повторения псевдослучайных чисел.
При использовании других процедур рандомизации следует помнить, что до их применения необходимо убедиться в качестве применяемых процедур.
Приведенные в настоящем стандарте таблицы псевдослучайных чисел могут быть использованы во всех случаях, когда это необходимо, в том числе при использовании стандартов, требующих применения таблиц случайных чисел.
^ В РФ действуют национальные стандарты:
ГОСТ Р ИСО 11648-1-2009 «Статистические методы. Выборочный контроль нештучной продукции. Часть 1. Общие принципы», идентичный международному стандарту ИСО 11648-1:2003 и
ГОСТ Р ИСО 11648-2-2009 «Статистические методы. Выборочный контроль нештучной продукции. Часть 2. Отбор выборки сыпучих материалов», идентичный международному стандарту ИСО 11648-2:2001.
V
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы ПРОЦЕДУРЫ РАНДОМИЗАЦИИ И ОТБОРА СЛУЧАЙНОЙ ВЫБОРКИ
Statistical methods. Randomization and random sampling procedures
Дата введения —2013—12—01
1 Область применения
Настоящий стандарт устанавливает процедуры рандомизации и случайного отбора выборки. Представленные в настоящем стандарте процедуры охватывают методы, предусматривающие применение технических средств, таблиц случайных чисел, компьютерных программ. Для компьютерных программ приведены общее описание соответствующего алгоритма и текст программы.
Настоящий стандарт применим в ситуациях, когда в требованиях технического регулирования, договора или другого стандарта установлено применение случайного отбора выборки или рандомизации. Методы случайного отбора выборки применимы при:
a) проведении статистического приемочного контроля дискретных единиц продукции, представленных на контроль в партиях;
b) отборе выборки для целей наблюдений и исследований;
c) проведении аудита системы менеджмента качества;
d) выборе экспериментальных единиц, порядка их обработки и проверки при выполнении плана эксперимента.
В настоящий стандарт также включена информация по случайному отбору выборки или рандомизации результатов, которая может быть использована специалистами службы качества и контролирующих органов при проведении аудита или проверок.
В настоящем стандарте представлены не все возможные способы применения процедур случайного отбора выборки и рандомизации и не все возможные стратегии отбора выборки и определения объема выборки. В соответствующих ситуациях следует использовать стандарты, перечисленные во введении.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 3534-1 Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах (ISO 3534-1, Statistics — Vocabulary and symbols — Part 1: General statistical terms and terms used in probability)
ИСО 3534-2 Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика (ISO 3534-2, Statistics — Vocabulary and symbols — Part 2: Applied statistics)
ИСО 3534-3 Статистика. Словарь и условные обозначения. Часть 3. Планирование эксперимента (ISO 3534-3, Statistics — Vocabulary and symbols — Part 3: Design of experiments)
ИСО 80000-2 Величины и единицы. Часть 2. Математические символы и знаки для применения в естественных науках и технологиях (ISO 80000-2, Quantities and units — Part 2: Mathematical signs and symbols to be used in the natural sciences and technology)
Издание официальное
3 Термины, определения и обозначения
В настоящем стандарте применены термины по ИСО 3534-1, ИСО 3534-2, ИСО 3534-3, а также следующие термины с соответствующими определениями.
3.1 Термины и определения
3.1.1 кластер (cluster): Часть совокупности (3.1.6), представляющей собой объединение непересека-ющихся групп выборочных единиц (3.1.13), выделенная в соответствии с установленным правилом.
[ИСО 3534-2:2006,1.2.28]
3.1.2 кластерный отбор (cluster sampling): Отбор выборки (3.1.12), при котором отбирают случайные выборки (3.1.8) из кластеров (3.1.1), и все отобранные выборочные единицы (3.1.13) объединяют в общую выборку (3.1.11).
[ИСО 3534-2:2006,1.3.9]
3.1.3 изменение порядка, полная перестановка (derangement complete permutation): Такая перестановка элементов набора1*, при которой ни один элемент не остается на своем исходном месте (например, набор цифр {3,1,2} представляет собой полную перестановку элементов набора {1,2,3}).
3.1.4 контролируемая партия (lot): Определенная часть совокупности (3.1.6), составленная для выборочного контроля и отражающая свойства совокупности.
Примечание — Целями выборочного контроля могут быть, например, определение оценки среднего некоторой характеристики или принятие решения о приемке или отклонении партии.
[ИСО 3534-2:2006,1.2.4]
3.1.5 многостадийный отбор (multistage sampling): Отбор (3.1.12), при котором выборку (3.1.1 ^отбирают в несколько приемов (стадий), выборочные единицы (3.1.13) на каждой стадии отбирают изболев крупных выборочных единиц, отобранных на предыдущей стадии.
Примечание — Многостадийный отбор выборки отличается от многокритериального отбора выборки. Многокритериальный отбор выборки представляет собой отбор выборки в соответствии с несколькими критериями одновременно.
[ИСО 3534-2:2006,1.3.10]
3.1.6 совокупность (population): <reference> Множество всех исследуемых единиц.
[ИСО 3534-2:2006,1.2.1]
3.1.7 псевдонезависимый случайный отбор выборки (pseudo-independent random sampling): Отбор выборки (3.1.12), при котором выборку (3.1.11) из л выборочных единиц (3.1.13) отбирают из совокупности (3.1.6) в соответствии с таблицей случайных чисел или компьютерным алгоритмом, разработанным таким образом, что каждая из возможных комбинаций по л выборочных единиц имеет установленную вероятность отбора (см. также 4.4).
3.1.8 случайная выборка (random sample): Выборка (3.1.11), отобранная с помощью случайного отбора выборки (3.1.9).
3.1.9 случайный отбор выборки (random sampling): Отбор выборки (3.1.12), при котором выборку (3.1.11) из л выборочных единиц (3.1.13) отбирают из совокупности (3.1.6) таким образом, что все возможные комбинации по л выборочных единиц имеют равную вероятность быть отобранными.
[ИСО 3534-2:2006,1.3.5]
3.1.10 рандомизация (randomization): Процесс, с помощью которого единицы набора размещают в случайном порядке.
Примечание — Если из совокупности (3.1.6), состоящей из натуральных чисел от 1 до п, извлекать числа случайным образом (т. е. таким способом, при котором все числа имеют одинаковые шансы быть отобранными) одно за другим без возвращения, пока совокупность не будет исчерпана, то порядок отбора чисел называют случайным или рандомизированным.
Если эти п чисел связаны с п различными объектами или обработками, которые устанавливают в соответствии с порядком этих п чисел, то порядок объектов или обработок называют случайным или рандомизированным.
^ Набор — конечное множество элементов.
ГОСТ Р ИСО 24153-2012
3.1.11 выборка (sample): Подмножество совокупности (3.1.6), состоящее из одной или нескольких выборочных единиц (3.1.13).
[ИСО 3534-2:2006,1.2.17]
3.1.12 отбор выборки (sampling): Действия по извлечению или составлению выборки (3.1.11).
[ИСО 3534-2:2006,1.3.1]
3.1.13 выборочная единица, единица (sampling unit, unit): Один из элементов, составляющих выборку (3.1.11).
Примечание1 — Выборочная единица может содержать один или несколько объектов (например, коробок спичек), но для нее получают один результат испытаний или наблюдений.
Примечание2 — Выборочная единица может состоять из дискретных объектов или определенного количества нештучной продукции (материала).
[ИСО 3534-2:2006, 1.2.14]
3.1.14 отбор с возвращением (sampling with replacement): Отбор выборки (3.1.12), при котором каждую выборочную единицу (3.1.13) после отбора возвращают в совокупность (3.1.6) до отбора следующей выборочной единицы.
[ИСО 3534-2:2006, 1.3.15]
3.1.15 отбор без возвращения (sampling without replacement): Отбор выборки (3.1.12), при котором каждую выборочную единицу (3.1.13) отбирают из совокупности (3.1.6) только один раз (не возвращая ее в совокупность до отбора следующей выборочной единицы).
3.1.16 начальное число (seed): Число или набор чисел, используемых для инициализации алгоритма, используемого для псевдонезависимого случайного отбора выборки (3.1.7) или установления исходной точки в таблице случайных чисел.
3.1.17 простая случайная выборка (simple random sample): Выборка (3.1.11), отобранная методом отбора простой случайной выборки (3.1.18).
[ИСО 3534-2:2006, 1.2.24]
3.1.18 отбор простой случайной выборки (simple random sampling): Отбор выборки (3.1.12), при котором выборку (3.1.11) из л выборочных единиц (3.1.13) отбирают из совокупности (3.1.6) таким способом, что все возможные комбинации из л выборочных единиц имеют одинаковую вероятность быть отобранными.
[ИСО 3534-2:2006,1.3.4]
3.1.19 расслоенная выборка (stratified sampling): Выборка (3.1.11), отобранная таким образом, что выборочные единицы (3.1.13) отбирают из различных слоев (3.1.21) совокупности, причем каждый слой представлен в выборке хотя бы одной выборочной единицей.
[ИСО 3534-2:2006,1.3.6]
3.1.20 отбор расслоенной простой случайной выборки (stratified simple random sampling): Отбор выборки, при котором выборку формируют на основе отбора простой случайной выборки (3.1.18) из каждого слоя (3.1.21) совокупности.
[ИСО 3534-2:2006,1.3.7]
3.1.21 слой (stratum): Исчерпывающая часть совокупности, являющаяся более однородной относительно исследуемой характеристики, чем вся совокупность (3.1.6)4
[ИСО 3534-2:2006,1.2.29]
3.2 Обозначения
В настоящем стандарте использованы математические символы и обозначения в соответствии с ИСО 80000-2, а также следующие обозначения:
dj — /-я цифра, количество сторон монеты или граней игральной кости;
N —объем партии; л —объем выборки; л, —объем/-ой выборки;
U —равномерно распределенная случайная величина на открытом интервале (0,1); х, —/-е значение случайной величины х; у! —факториалу;
^ Слои совокупности являются непересекающимися, т. е. не содержат общих единиц.
3
М —функция округления z до ближайшего целого в большую сторону (наименьшее целое число, больше или равное действительному числу z);
LzJ —функция округления z до ближайшего целого в меньшую сторону (наибольшее целое число, равное действительному числу z или меньше его).
4 Основные положения
4.1 Применение случайного отбора выборки является необходимым условием правильного применения большей части планов выборочного контроля при контроле продукции на промышленных предприятиях. Применение рандомизации, использующей принципы случайного отбора выборки, необходимо также при планировании экспериментов, поскольку это повышает достоверность результатов эксперимента и обеспечивает использование статистических методов для их интерпретации. Целью случайного отбора выборки является обеспечение возможности применения теории вероятностей к практическим задачам. Эта цель не достижима при использовании других способов отбора выборки. Например, отбор выборки, основанный на принципах интуиции или личных предпочтений, позволяет случайно достичь хороших результатов, но при этом полученные оценки всегда имеют смещение и, следовательно, такой отбор выборки может привести к серьезным ошибкам при принятии решений. Случайный отбор выборки направлен на устранение смещения путем обеспечения равной вероятности отбора в выборку для каждой единицы (отбор с возвращением) или для каждой выборки данного объема (отбор без возвращения).
4.2 Равновероятным случайным отбором с возвращением является отбор, при котором вероятность отбора конкретной единицы партии, состоящей из N единиц, всегда равна 1/Л/. Существует Nn возможных вариантов отбора упорядоченной выборки объема п из Л/единиц и (Л/ + п- 1)!/[л!(Л/-1)!] вариантов отбора неупорядоченной случайной выборки объема п из N единиц (см. примечание ниже).
При отборе простой случайной выборки без возвращения вероятность того, что конкретная единица из партии объема N будет отобрана при отборе первой выборочной единицы, равна 1/Л/, M(N-1) — при отборе второй, 1/(Л/-2) —третьей и так далее. Если л выборочных единиц отобраны случайным образом из партии объема N без возвращения, то каждой комбинации из п единиц соответствует одинаковая вероятность отбора, равная вероятности одновременного отбора п единиц из N. Количество возможных различных неупорядоченных случайных выборок по п единиц из партии объема N (отличающихся только составом) равно N\/[n\(N - л)!], что представляет собой число сочетаний по п единиц из N. Количество возможных упорядоченных случайных выборок по п единиц, отобранных из партии в N единиц, без возвращения (отличающихся и составом и порядком расположения в выборке) равно Л/!/(Л/ - л)!, т. е. равно произведению числа сочетаний по л единиц из N на число перестановок из л единиц. Следует отметить, что случайная выборка без возвращения более всего распространена в качестве стратегии отбора выборки при статистическом приемочном контроле.
Примечание — При отборе выборки с возвращением, например, трех из пяти единиц, выборки {1,1,2), {1, 2, 1), и {2, 1, 1} различны, если учитывают порядок элементов, однако эти выборки не имеют различий, если порядок элементов не учитывают.
4.3 Случайный отбор выборки может быть получен только при строгом выполнении разработанных специальных процедур. В настоящем стандарте представлено несколько методик случайного отбора выборки. Методы, использующие специальные устройства, предполагают, что монеты и игральные кости имеют равные вероятности выпадения граней или сторон при броске, а сам бросок не вносит смещения. Учитывая трудности непосредственного выполнения методов отбора выборки с использованием калькулятора или компьютера (см. [9], [10], [12] и [13]), в настоящем стандарте приведен простой компьютерный метод генерации случайной выборки. Следует помнить, что при использовании всех приведенных ниже методов необходимо, чтобы каждой единице партии заранее было поставлено в соответствие число от 1 до N, так, чтобы выборочные единицы в партии в результате были однозначно идентифицированы.
4.4 При описании процедуры или метода случайного отбора выборки (см. [8]) прилагательное «псев-донезависимый» в тексте настоящего стандарта часто опущено. Кроме того, прилагательное «случайный» часто использовано в том смысле, что соответствующее существительное (число или перестановка) является результатом процесса, который случайным образом генерирует такое число или перестановку. В представленных примерах для наглядности использованы небольшие объемы выборки.
5 Описание процедур случайного отбора выборки. Методы, использующие специальные устройства
5.1 Метод урны
5.1.1 В урну помещают N четко пронумерованных идентичных объектов (например билеты, пластинки, шары), однозначно представляющих каждую из N единиц партии и хорошо их перемешивают.
5.1.2 Для отбора без возвращения, вслепую выбирают объекты из урны, один за другим, не возвращая их в урну, и произвольно перемешивая объекты между выемками, пока не будет получено необходимое количество п выборочных единиц.
Примечание — Этот метод обычно используют в лотереях.
5.1.3 Для отбора с возвращением, вслепую выбирают объекты из урны один за другим, возвращая отобранный объект в урну после каждой выемки, и полностью перемешивая объекты между выемками, пока не будет получено необходимое количество п выборочных единиц. При использовании этого метода одна и та же единица может быть отобрана в выборку несколько раз.
5.2 Метод монет или игральных костей
5.2.1 Определяют количество т монет или игральных костей (бросков монеты или игральной кости) по следующей формуле (Л/—объем партии, к— количество сторон или граней используемого объекта)
т - ПпЛ//1п/с1.
5.2.2 При использовании нескольких монет или игральных костей устанавливают четкое соответствие каждой монеты или кости определенной цифре в последовательности цифр (ф,..., dm). При использовании единственной монеты или кости устанавливают соответствие результата первого броска цифре ф, второго броска — цифре d2 и так далее.
5.2.3 Бросают монету или игральную кость и записывают т значений ф (i=\m). Трансформируют полученные результаты в десятичное целое число по следующей формуле
т
у = 1 + £(d, -1 )кт~'.
/=1
5.2.4 Повторяют действия в соответствии с 5.2.3, отбрасывая все значения, превышающие N, и (при отборе выборки без возвращения) все значения, отобранные ранее, до получения п выборочных единиц.
Пример 1—Контролеру необходима случайная выборка объемом 4 единицы из партии в 20 единиц. Для формирования выборки он использует единственную монету. В соответствии с 5.2.1 для получения каждого случайного числа необходимо выполнить т = 5 бросков монеты. Определено, что одна сторона монеты соответствует цифре 1, а другая - цифре 2. Первая последовательность бросков дает набор чисел {1, 2, 1, 2, 2), который в соответствии с 5.2.3 дает число 1 + (0) ■ 2* + (1) ■ 23 + (0) ■ 22 + (1) ■ 21 + + (1) ■ 2° = 12. Следующие три последовательности бросков дают наборы {1,2,2,2,1}, {1,1,2,2,1} и {2,2,1, 2,2), которые дают числа 15,7 и 28 соответственно. Так как значение 28 превышает объем партии, его отбрасывают, и выполняют броски, пока не будет получено еще одно действительное число, необходимое для формирования случайной выборки.
Пример 2—Необходимо отобрать случайную выборку с объемом 4 единицы из партии в 50 единиц. Для формирования выборки контролер использует несколько шестигранных игральных костей различного цвета. В соответствии с 5.2.1 необходимо для получения каждого случайного числа т = 3 игральные кости. Выпавшее значение синей, зеленой и красной игральных костей контролер записывает в том же порядке (синяя, зеленая, красная). Однако уравнение 5.2.3 позволяет получить действительные числа из интервала от 1 до 50 только в том случае, когда первая игральная кость дает значения 1 или 2. Следовательно, работа может быть упрощена, если выпавшие значения синей кости будут преобразованы в 1 или 2 без изменения вероятности результата. Контролер решает заранее, что нечетные выпавшие значения синей кости будет рассматривать как 1, а четные — как 2. Первый бросок дает {3, 3,4}, который в соответствии с 5.2.3 дает число 1 + (2)-62 + (2)-61 + (3)-6° = 88 (слишком большое), которое после преобразования к {1,3, 4} дает 16. Еще три броска дают {6, 1, 3} (после преобразования {2,1, 3}), {5, 6, 6} (после преобразования {1,6,6}) и {2,5,5} (после преобразования {2,5,5}), которые в соответствии с 5.2.3 дают значения 39,36 и 65 соответственно. Так как значение 65 превышает объем партии, его необходимо отбросить и выполнить дополнительные броски, пока не будет получено еще одно действительное число.
5