ГОСТ Р ИСО 16610-21-2015
Государственная система обеспечения единства измерений. Геометрические характеристики изделий (ГХИ). Фильтрация. Часть 21. Линейные профильные фильтры. Фильтры Гаусса
Описывает метрологические характеристики фильтра Гаусса, применительно к фильтрации профиля. В том числе указываются методы разделения коротковолновых (высокой пространственной частоты) и длинноволновых (низкой пространственной частоты) компонент поверхностного профиля.
Идентичен ISO 16610-21:2011
Переиздание. Март 2019 г.
Оглавление
1 Область применения
2 Нормативные ссылки
3 Термины и определения
4 Характеристики Гауссова фильтра профиля для открытого профиля
5 Характеристики Гауссова фильтра профиля для замкнутого профиля
Приложение A (справочное) Ошибки, возникающие на практике, для открытых и замкнутых профилей (алгоритм сшивки)
Приложение B (справочное) Примеры
Приложение C (справочное) Место в матрице фильтров
Приложение D (справочное) Место в матрице ГХИ
Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов ссылочным национальным стандартам
Библиография
28 страниц
| Дата введения | 01.06.2016 |
|---|---|
| Добавлен в базу | 01.02.2017 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
Организации:
| 22.09.2015 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 1362-ст |
|---|---|---|---|
| Разработан | ФГУП ВНИИОФИ | ||
| Издан | Стандартинформ | 2016 г. | |
| Издан | Стандартинформ | 2019 г. |
State system for ensuring the traceability of measurements. Geometrical product specifications (GPS). Filtration. Part 21. Linear profile filters. Gaussian filters
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8
стр. 9
стр. 10
стр. 11
стр. 12
стр. 13
стр. 14
стр. 15
стр. 16

стр. 17
стр. 18
стр. 19
стр. 20

стр. 21
стр. 22

стр. 23
стр. 24
стр. 25

стр. 26

стр. 27

стр. 28
ГОСТ Р исо
16610-21-
2015
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
НАЦИОНАЛЬНЫЙ
СТАНДАРТ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
Государственная система обеспечения единства измерений
Геометрические характеристики изделий (ГХИ) ФИЛЬТРАЦИЯ
Часть 21
Линейные профильные фильтры. Фильтры Гаусса
(ISO 16610-21:2011, ЮТ)
Ш
Издание официальное
Москва
Стандартинформ
2016
Предисловие
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт оптико-физических измерений» (ФГУП «ВНИИОФИ») на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 206 «Эталоны и поверочные схемы»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 22 сентября 2015 г. № 1362-ст
4 Настоящий стандарт идентичен международному стандарту ИС016610-21:2011 «Геометрические характеристики изделий (ГХИ). Фильтрация. Часть 21. Линейные профильные фильтры. Фильтры Гаусса» (IS016610-21:2011 «Geometrical product specifications (GPS) — Filtration — Part 21: Linear profile filters: Gaussian filters», IDT).
Международный стандарт разработан Техническим комитетом ИСО/ТС 213 «Пространственные и геометрические спецификации продуктов и верификация».
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в ГОСТ Р 1.0-2012 (раздел 8). Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии сети Интернет (www.gost.ru)
© Стандартинформ, 2016
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
ГОСТ Р ИСО 16610-21-20154.3 Краевые эффекты
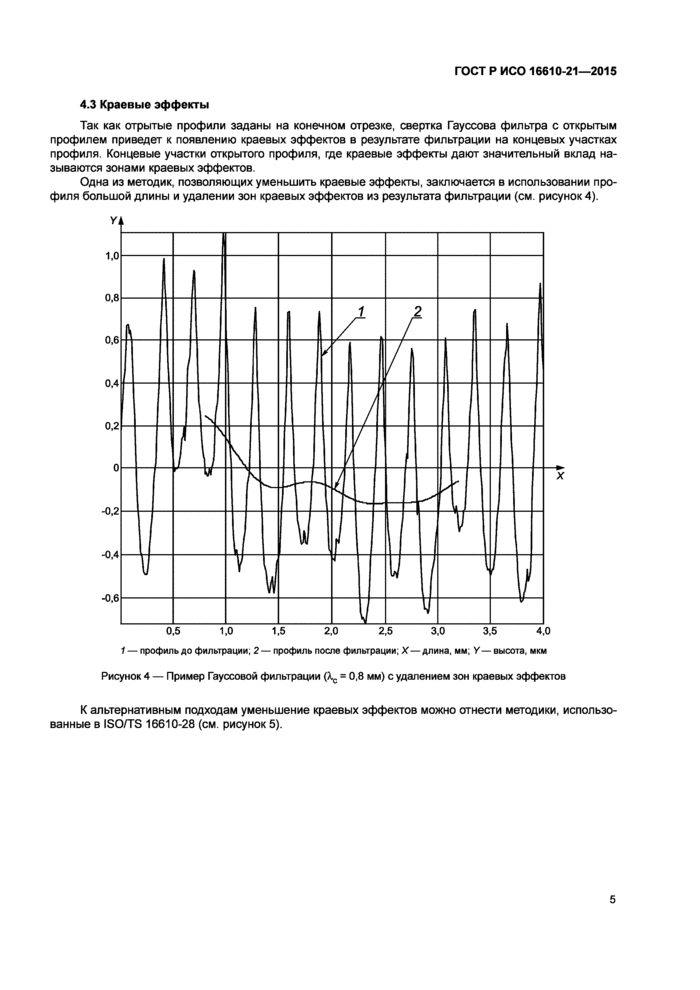
Так как отрытые профили заданы на конечном отрезке, свертка Гауссова фильтра с открытым профилем приведет к появлению краевых эффектов в результате фильтрации на концевых участках профиля. Концевые участки открытого профиля, где краевые эффекты дают значительный вклад, называются зонами краевых эффектов.
Одна из методик, позволяющих уменьшить краевые эффекты, заключается в использовании профиля большой длины и удалении зон краевых эффектов из результата фильтрации (см. рисунок4).
|
1 — профиль до фильтрации; 2 — профиль после фильтрации; X—длина, мм; У— высота, мкм Рисунок 4 — Пример Гауссовой фильтрации (Хс = 0,8 мм) с удалением зон краевых эффектов |
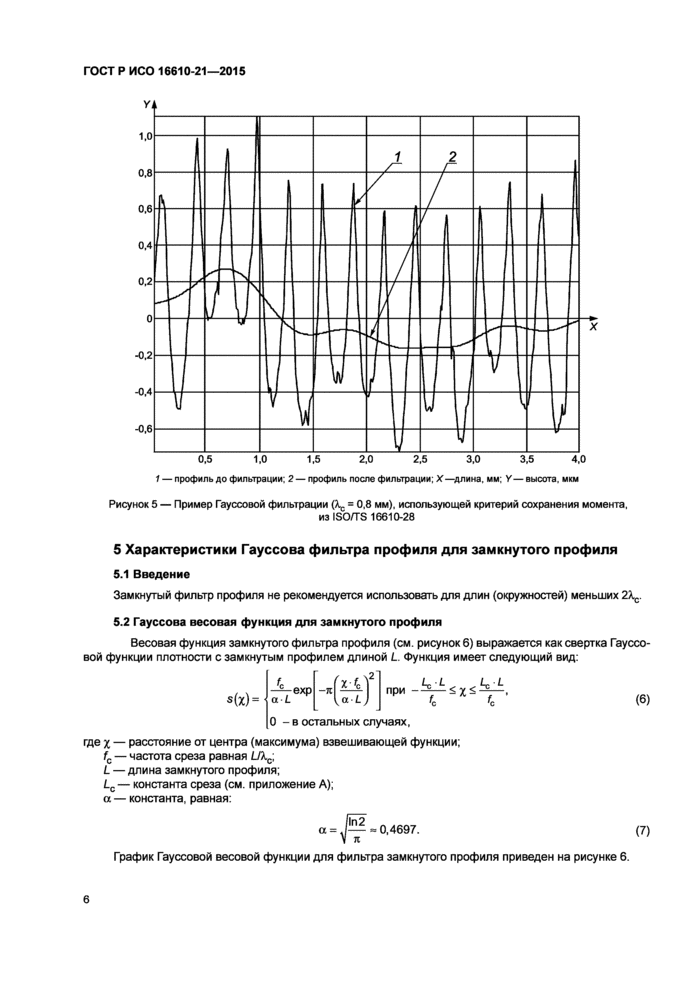
К альтернативным подходам уменьшения краевых эффектов можно отнести методики, использованные в ИСО/ТС 16610-28 (см. рисунок 5).
5
|
1 — профильдо фильтрации; 2 — профиль после фильтрации;Х—длина, мм; Y— высота, мкм Рисунок 5 — Пример Гауссовой фильтрации (Хс = 0,8 мм), использующей критерий сохранения момента, из ИСО/ТС 16610-28 |
5 Характеристики Гауссова фильтра профиля для замкнутого профиля
5.1 Введение
Замкнутый фильтр профиля не рекомендуется использовать для длин (окружностей), меньших 2^.
5.2 Гауссова весовая функция для замкнутого профиля
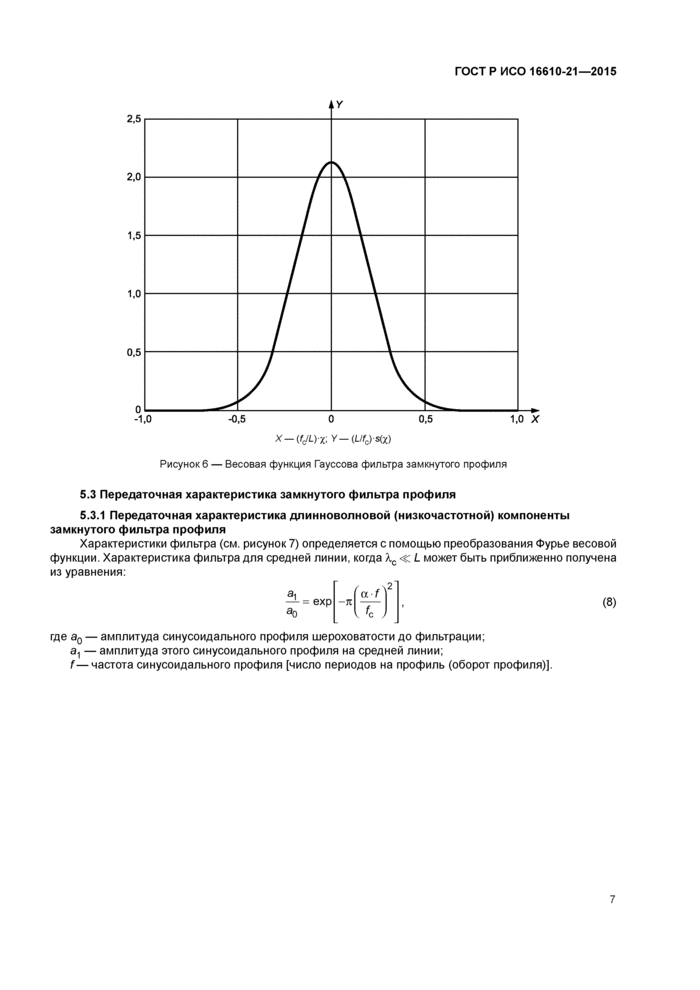
Весовая функция замкнутого фильтра профиля (см. рисунок 6) выражается как свертка Гауссовой функции плотности с замкнутым профилем длиной L. Функция имеет следующий вид:
'н,
s(x) =
-exp
a L
L.L . , LCL
при—c— <%< s—,
•r. 'n
(6)
0 — в остальных случаях,
где х — расстояние от центра (максимума) взвешивающей функции; fc — частота среза, равная U\.\
L — длина замкнутого профиля;
Lc — константа среза (см. приложение А); а — константа, равная:
а = ^ * 0,4697.
(7)
6
Г рафик Г ауссовой весовой функции для фильтра замкнутого профиля приведен на рисунке 6.
|
X-(fc/L)r,Y-(L/fc)s(X) Рисунок 6 — Весовая функция Гауссова фильтра замкнутого профиля |
5.3 Передаточная характеристика замкнутого фильтра профиля5.3.1 Передаточная характеристика длинноволновой (низкочастотной) компоненты замкнутого фильтра профиля
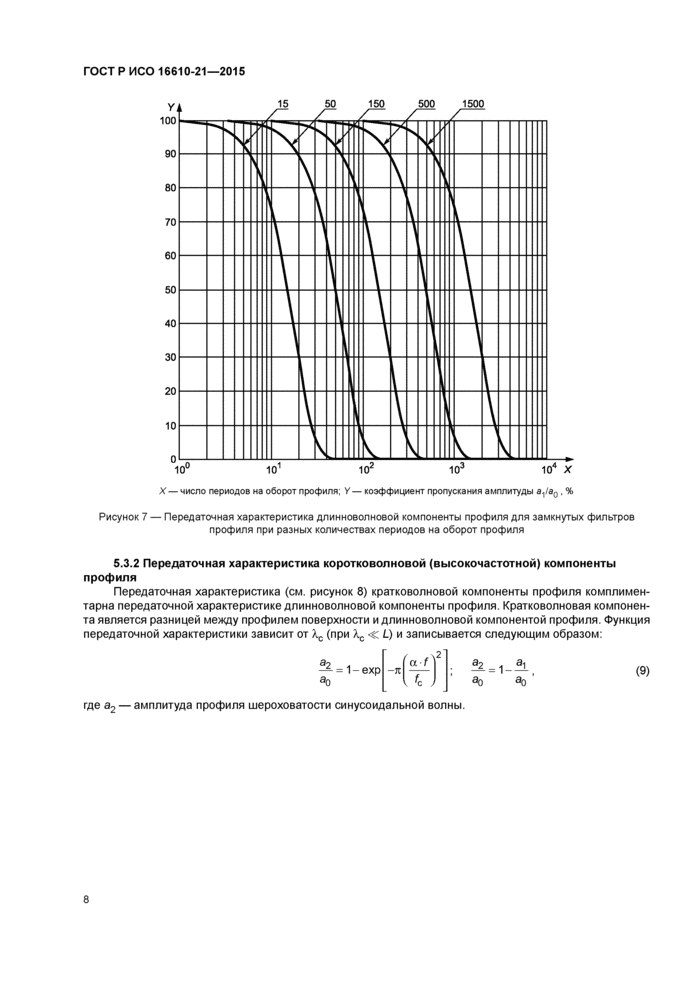
Характеристика фильтра (см. рисунок7) определяется с помощью преобразования Фурье весовой функции. Характеристика фильтра для средней линии, когда \ « L, может быть приближенно получена из уравнения:
|
( хЛ2 | |
|
-п |
а • f I |
|
f 1 | |
|
^ с J |
где а0 — амплитуда синусоидального профиля шероховатости до фильтрации; а1 — амплитуда этого синусоидального профиля на средней линии;
f— частота синусоидального профиля [число периодов на профиль (оборот профиля)].
5.3.2 Передаточная характеристика коротковолновой (высокочастотной) компоненты профиля
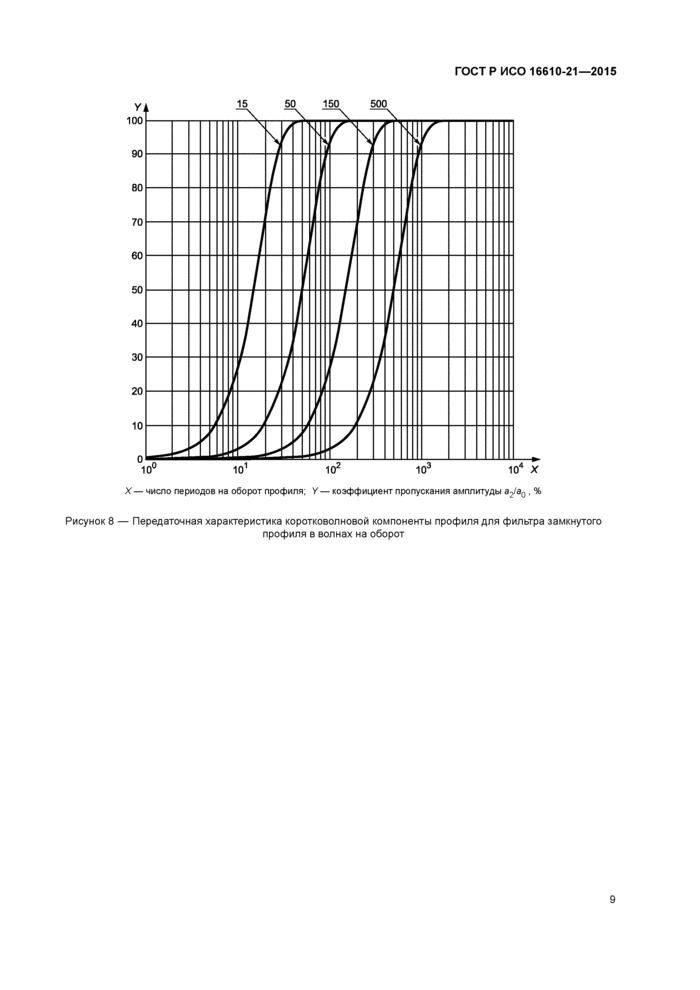
Передаточная характеристика (см. рисунок 8) коротковолновой компоненты профиля комплиментарна передаточной характеристике длинноволновой компоненты профиля. Коротковолновая компонента является разницей между профилем поверхности и длинноволновой компонентой профиля. Функция передаточной характеристики зависит от ^ (при \ «Ц\л записывается следующим образом:
а2
а0
|
а2 а0 |
(9)
где а2 — амплитуда профиля шероховатости синусоидальной волны.
7
|
X — число периодов на оборот профиля; Y — коэффициент пропускания амплитуды а^1а0, % Рисунок 7 — Передаточная характеристика длинноволновой компоненты профиля для замкнутых фильтров профиля при разных количествах периодов на оборот профиля |
8
|
X — число периодов на оборот профиля; Y — коэффициент пропускания амплитуды а2/а0, % Рисунок 8 — Передаточная характеристика коротковолновой компоненты профиля для фильтра замкнутого профиля в волнах на оборот |
9
Приложение А (справочное)
Ошибки, возникающие на практике, для открытых и замкнутых профилей
(алгоритм сшивки)
А.1 Открытые профили
В теории весовая функция Гаусса для открытого профиля принимает положительное значение, когда задана в диапазоне от минус бесконечности до плюс бесконечности. Однако весовая функция Гаусса быстро убывает при удалении от центра, так что в областях, достаточно удаленных от него, она практически равна нулю. Другими словами, на практике, весовая функция Гаусса задана в ограниченной области. Ограниченная весовая функция Гаусса имеет следующий вид:
ГО при х < -/-с ■ А.с;
s(x)= s(x)npn-Lc-A.c <%<Lc-\; (А.1)
[о при %> Lc- \с.
где х — расстояние вдоль профиля от центра (максимума) весовой функции;
А,с — длина волны среза;
Lc — константа среза.
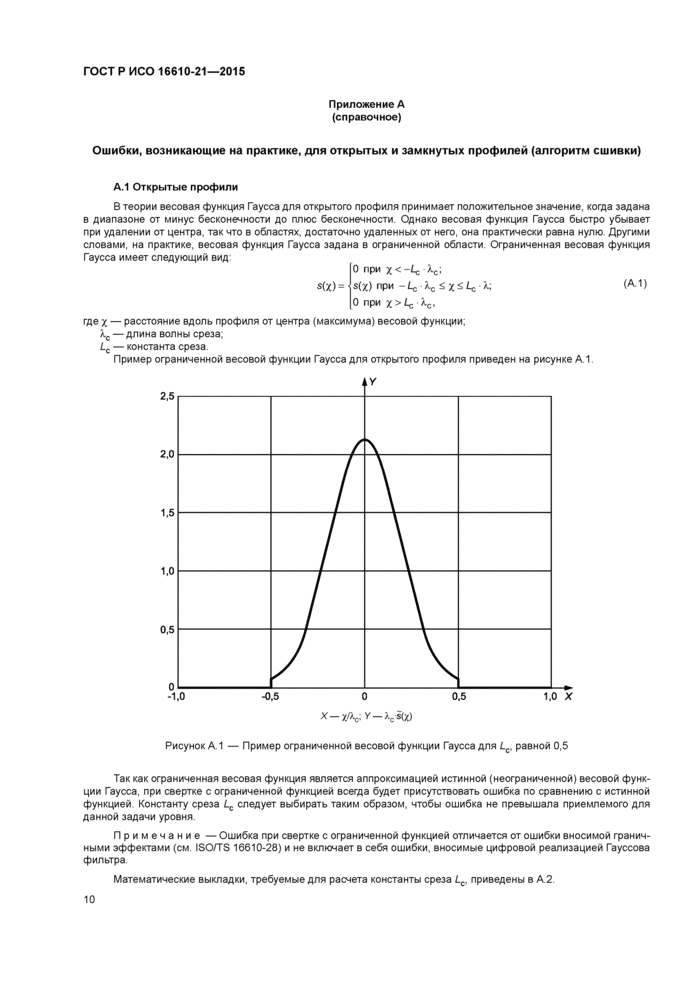
Пример ограниченной весовой функции Г аусса для открытого профиля приведен на рисунке А.1.
Х-х\\ Y-Xc s(x)
Рисунок А.1 — Пример ограниченной весовой функции Гаусса для Lc, равной 0,5
Так как ограниченная весовая функция является аппроксимацией истинной (неограниченной) весовой функции Гаусса, при свертке с ограниченной функцией всегда будет присутствовать ошибка по сравнению с истинной функцией. Константу среза Lc следует выбирать таким образом, чтобы ошибка не превышала приемлемого для данной задачи уровня.
10
Примечание — Ошибка при свертке с ограниченной функцией отличается от ошибки, вносимой граничными эффектами (см. ИСО/ТС 16610-28), и не включает в себя ошибки, вносимые цифровой реализацией Гауссова фильтра.
Математические выкладки, требуемые для расчета константы среза /_с, приведены в А.2.
А.2 Математика для открытого профиля
С точки зрения математики, ограничение весовой функции до конечного интервала1) может быть описано с помощью умножения на прямоугольную функцию, таким образом ограниченная весовая функция может быть записана следующим образом:
s(x) = s(x)-r(Lc, х), (А.2)
где s(x) — весовая функция Гаусса;
s(x) — ограниченная весовая функция Гаусса; r(Lc, х) — прямоугольная функция, описываемая:
(А.З)
|1 при Lc-Xc <%<Lc-\-,
[О —в остальных случаях.
Ошибка, возникающая из-за ограничения интервала, определяется максимальным отклонением между передаточной функцией ограниченной весовой функции от передаточной функции неограниченной весовой функции.
Преобразование Фурье ограниченной весовой функции Гаусса§(ю)
00
§(ю) = (S• R){a>) = JS(v)- R{Lc, ю -v)dv, (А.4)
-00
где S(v) — Фурье образ весовой функции Г аусса;
R(.,.) — Фурье образ прямоугольной функции, который может быть представлен как:
R(Lc, ш) = 'j е-'И)Ух = 2Lc Хс • sine mj , (А.5)
“А
где функция sine (%) = sin
erfc
Согласно уравнению (А.З) при м = 0 достигается максимальное отклонение между передаточными функциями ограниченной и неограниченной весовых функций,что приводит к максимальной погрешности1);
а - А..
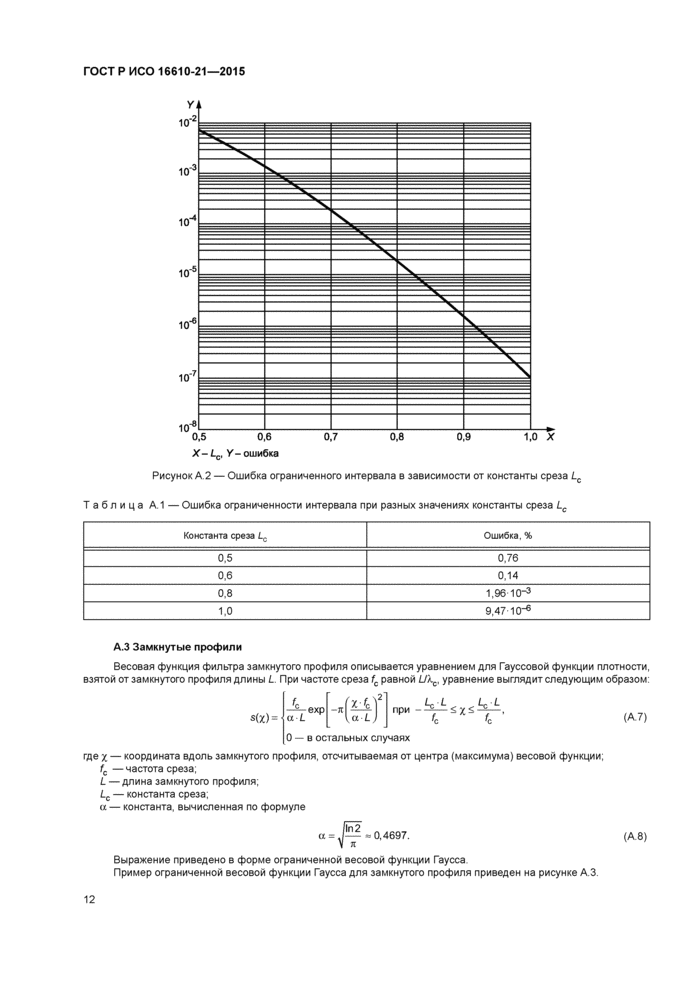
Ее график приведен на рисунке (см. рисунок А.2), а также функция может быть описана в виде таблицы (см. таблицу А.1).
См. [6].
11
|
Рисунок А.2 — Ошибка ограниченного интервала в зависимости от константы среза Lc |
|
Таблица А.1 — Ошибка ограниченности интервала при разных значениях константы среза Lc | ||||||||||
| ||||||||||
|
На профиле w(%) оценка максимальной ошибки может быть получена следующим образом1); |
A“(x)^Pm axerfC
где дтах — максимальное абсолютное значение профиля.
А.З Замкнутые профили
Весовая функция фильтра замкнутого профиля описывается уравнением для Гауссовой функции плотности, взятой отзамкнутого профиля длины L. При частоте среза fc, равной UXC, уравнение выглядит следующим образом:
ч 2”
(А.6)
s(x):
a L
ехр
при - -
LrL
(А.7)
О — в остальных случаях
где х — координата вдоль замкнутого профиля, отсчитываемая от центра (максимума) весовой функции; fc — частота среза;
L — длина замкнутого профиля;
1 См. [6].
Lc — константа среза; а — константа, вычисленная по формуле
а = л1^ « 0,4697. (А-8)
V п
Выражение приведено в форме ограниченной весовой функции Гаусса.
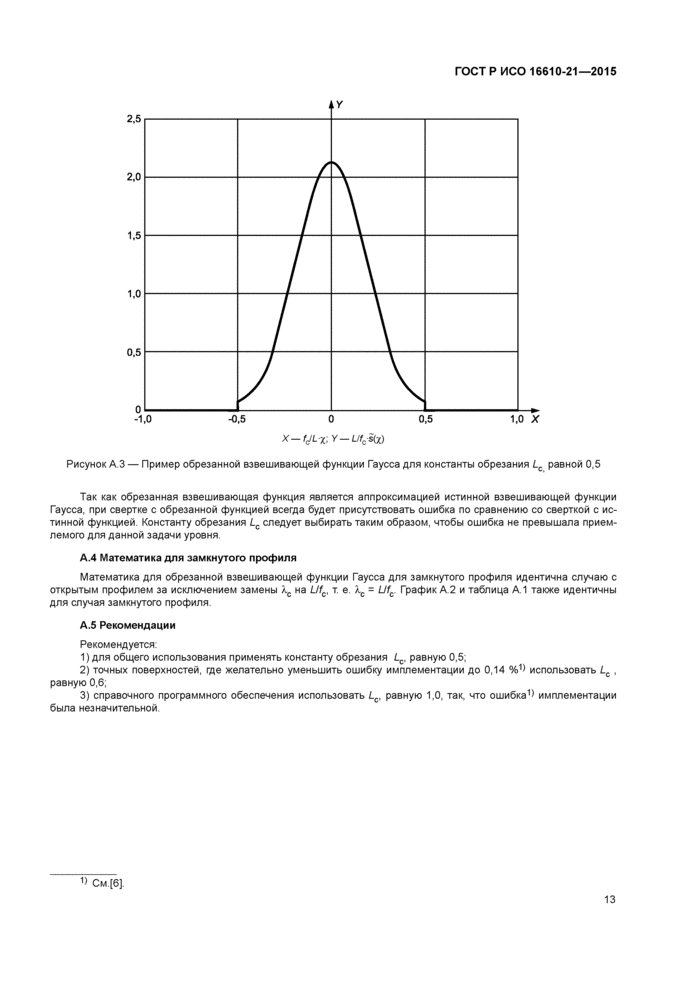
Пример ограниченной весовой функции Гаусса для замкнутого профиля приведен на рисунке А.З.
|
X— fciL■ х; Y— Llfc-s(%) |
Рисунок А.З — Пример обрезанной взвешивающей функции Гаусса для константы обрезания Lc, равной 0,5
Так как обрезанная взвешивающая функция является аппроксимацией истинной взвешивающей функции Гаусса, при свертке с обрезанной функцией всегда будет присутствовать ошибка по сравнению со сверткой с истинной функцией. Константу обрезания /_с следует выбирать таким образом, чтобы ошибка не превышала приемлемого для данной задачи уровня.
А.4 Математика для замкнутого профиля
Математика для обрезанной взвешивающей функции Гаусса для замкнутого профиля идентична случаю с открытым профилем за исключением замены Хс на Ufc, т. е. А,с = Ufc. График А.2 и таблица А. 1 также идентичны для случая замкнутого профиля.
А.5 Рекомендации
Рекомендуется:
1) для общего использования применять константу обрезания /_с, равную 0,5;
2) для точных поверхностей, где желательно уменьшить ошибку имплементации до 0,14 “/о1), использовать Lc, равную 0,6;
3) для справочного программного обеспечения использовать Lc, равную 1,0, так, чтобы ошибка1) имплементации была незначительной.
См. [6].
13
Приложение В (справочное)
Примеры
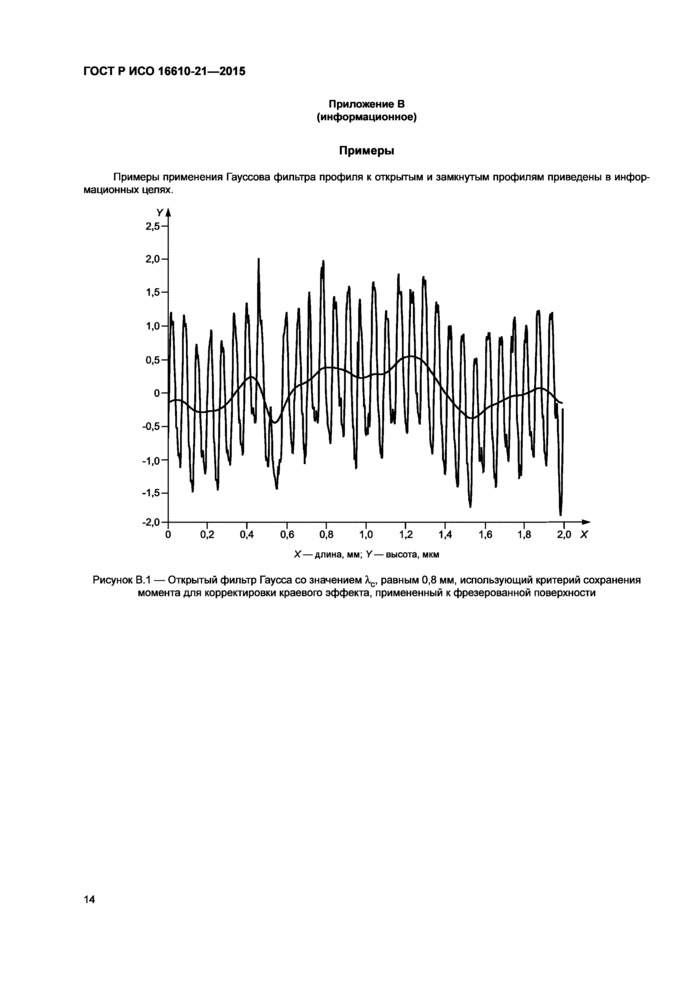
Примеры применения Гауссова фильтра профиля к открытым и замкнутым профилям приведены в информационных целях.
|
X — длина, мм, Y — высота, мкм |
Рисунок В.1 — Открытый фильтр Гаусса со значением Хс, равным 0,8 мм, использующий критерий сохранения момента для корректировки краевого эффекта, примененный к фрезерованной поверхности
14
Содержание
1 Область применения...................................................1
2 Нормативные ссылки..................................................1
3 Термины и определения................................................2
4 Характеристики Гауссова фильтра профиля для открытого профиля....................2
5 Характеристики Гауссова фильтра профиля для замкнутого профиля....................6
Приложение А (справочное) Ошибки, возникающие на практике, для открытых и замкнутых
профилей (алгоритм сшивки)....................................10
Приложение В (справочное) Примеры........................................14
Приложение С(справочное) Место в матрице фильтров.............................16
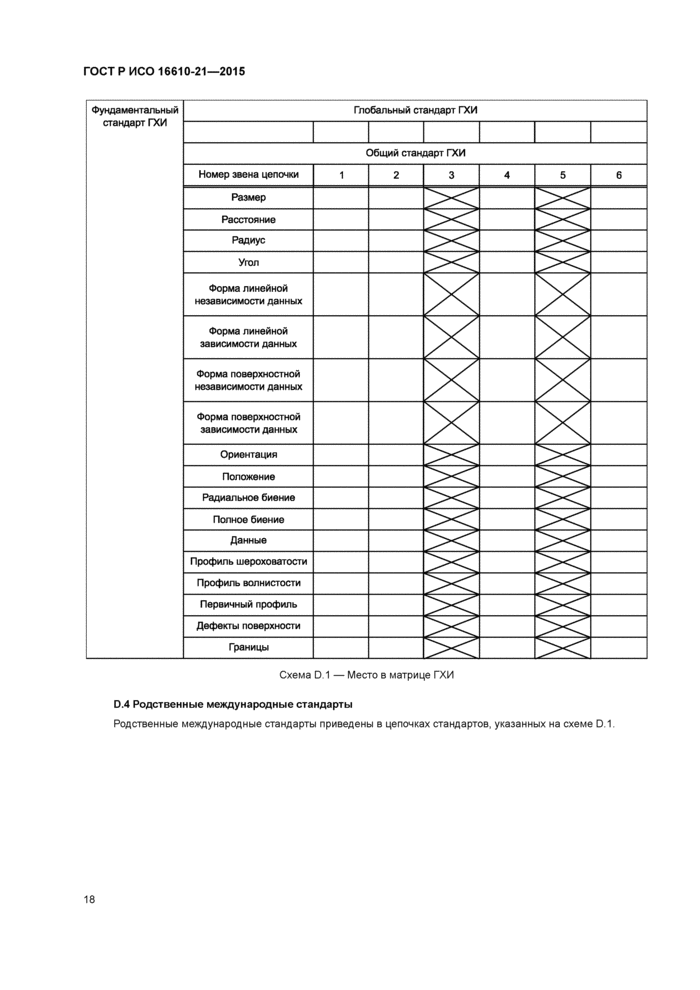
Приложение D (справочное) Место в матрице ГХИ................................17
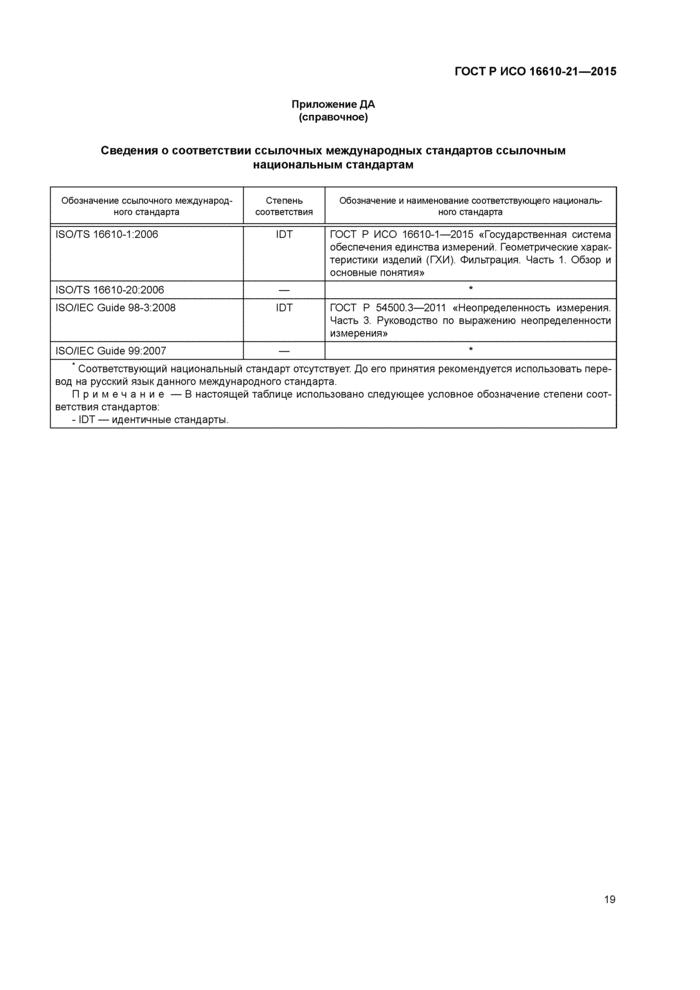
Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов
ссылочным национальным стандартам Российской Федерации.............19
Библиография........................................................20
|
270 |
Рисунок В.2 — Замкнутый фильтр Гаусса (со значением fc = 5 периодов на оборот), примененный к фрезерованной/штампованной поверхности
15
Предисловие к международному стандарту ИСО 16610-21:2011
ИСО (Международная Организация Стандартизации) представляет собой всемирную федерацию национальных стандартизационных подразделений. Мероприятия по подготовке международных стандартов обычно выполняются через технические комитеты ИСО. Каждое национальное подразделение, заинтересованное в теме, для которой был организован технический комитет, имеет право на представительство в этом комитете. Международные организации, правительственные и неправительственные, поддерживающие отношения с ИСО, также принимают участие в работах. ИСО тесно сотрудничает с Международной Электротехнической Комиссией (МЭК) во всех вопросах, связанных с электротехнической стандартизацией.
Международные стандарты подготавливаются в соответствии с правилами, установленными в ИСО/МЭК Директивы. Часть 2.
Основной задачей технических комитетов является подготовка международных стандартов. Международные стандарты, разрабатывающиеся техническими комитетами, передаются национальным подразделениям для голосования. Публикация и принятие международного стандарта требует одобрения как минимум 75 % национальных подразделений, участвующих в голосовании.
Следует принять во внимание, что существует вероятность, что некоторые элементы этого документа являются субъектами патентных прав. ИСО не несет ответственности за идентификацию части или всех подобных вопросов.
ИСО 16610-21:2011 разработан Техническим комитетом ИСО/ТС 213 «Пространственные и геометрические спецификации продуктов и верификация».
В результате технического пересмотра ИСО 16610-21 отменяет и заменяет собой стандарт ИСО 11562:1996.
ИСО 16610 под общим заголовком «Геометрические характеристики изделий (GPS). Фильтрация» включает в себя следующие разделы:
- часть 1. Обзор и основные понятия;
- часть 20. Фильтры линейного профиля. Основные понятия;
- часть 21. Фильтры линейного профиля. Фильтры Гаусса;
- часть 22. Фильтры линейного профиля. Сплайн-фильтры;
- часть 28. Фильтры линейного профиля. Сплайн-Вейвлеты;
- часть 29. Линейные фильтры профиля. Сплайновые вейвлеты;
- часть 30. Робастные фильтры профиля. Основные понятия;
- часть 31. Робастные фильтры профиля. Регрессионный фильтр Гаусса;
- часть 32. Робастные фильтры профиля. Сплайн-фильтры;
- часть 40. Морфологические фильтры профиля. Базовые понятия;
-часть 41. Морфологические фильтры профиля. Дисковые и линейно-сегментные горизонтальные фильтры;
- часть 49. Морфологические фильтры профиля. Техники масштабирования пространства.
Следующие части находятся в стадии разработки:
- часть 26. Фильтры линейного профиля. Фильтрация по номинально ортогональным плоским сеткам наборов данных;
- часть 27. Фильтры линейного профиля. Фильтрация по номинально ортогональным цилиндрическим сеткам наборов данных;
- часть 42. Морфологические фильтры профиля. Узорные фильтры;
- часть 60. Линейные поверхностные фильтры. Основные понятия;
- часть 61. Линейные поверхностные фильтры. Фильтры Гаусса;
- часть 62. Линейные поверхностные фильтры. Сплайн-фильтры;
- часть 69. Линейные поверхностные фильтры. Сплайн-вейвлеты;
- часть 70. Робастные поверхностные фильтры. Основные понятия;
- часть 71. Робастные поверхностные фильтры. Регрессионный фильтр Гаусса;
- часть 72. Робастные поверхностные фильтры. Сплайн-фильтры;
- часть 80. Морфологические поверхностные фильтры. Основные понятия;
-часть 81. Морфологические поверхностные фильтры. Сферические и горизонтально-плоскостные сегментные фильтры;
- часть 82. Морфологические поверхностные фильтры. Узорные фильтры;
- часть 89. Морфологические поверхностные фильтры. Техники масштабирования пространства.
IV
ГОСТ Р ИСО 16610-21-2015Введение
к международному стандарту ИСО 16610-21:2011
Данная часть ИСО/ТС 16610 является Технической Спецификацией геометрических характеристик изделия и должна рассматриваться в качестве общей Технической Спецификации (см. ИСО/ТР 14638). Она влияет на звенья 3 и 5 во всей цепочке стандартов.
Генеральный план ИСО/ГХИ, приведенный в ИСО/ТР 14638, дает обзор системы ИСО/ГХИ, частью которого является стандарт ИСО 16610-21. Фундаментальные правила ИСО/ГХИ, объявленные в ИСО 8015, применяют к ИСО 16610-21, а также стандартные правила принятия решений, приведенные в ИСО 14253-1, применяют к спецификациям, сделанным в соответствии с ИСО 16610-21, в случае, если не оговорено иное.
Детальная информация о соотношении ИС016610-21 с матричной моделью ГХИ приведена в приложении D.
Стандарт ИСО 16610-21 устанавливает терминологию и понятия Гауссовых фильтров. Она имеет передачи для отключения волны как 50 %, поскольку коротковолновые и длинноволновые компоненты поверхностного профиля разделены и могут быть восстановлены без изменения профиля поверхности.
V
Введениек национальному стандарту Российской Федерации
Цель настоящего стандарта — прямое применение в Российской Федерации международного стандарта ИСО 16610-21:2011 «Геометрические характеристики изделий (ГХИ). Фильтрация. Часть 21. Линейные профильные фильтры. Фильтры Гаусса» как основы для изготовления и поставки объекта стандартизации по договорам (контрактам) на экспорт.
VI
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИГосударственная система обеспечения единства измерений Геометрические характеристики изделий (ГХИ)ФИЛЬТРАЦИЯ
ФИЛЬТРАЦИЯ
Часть 21
Линейные профильные фильтры Фильтры Гаусса
State system for ensuring the uniformity of measurements. Geometrical product specifications (GPS). Filtration. Part 21. Linear profile filters. Gaussian filters
Дата введения — 2016—06—01
1 Область применения
Настоящий стандарт описывает метрологические характеристики фильтра Гаусса, применительно к фильтрации профиля. В том числе указываются методы разделения коротковолновых (высокой пространственной частоты) и длинноволновых (низкой пространственной частоты) компонент
поверхностного профиля.
2 Нормативные ссылки
Нижеследующие документы, на которые приводятся ссылки, являются обязательными для применения настоящего стандарта. В отношении датированных ссылок действительно только указанное издание. В отношении недатированных ссылокдействительно последнее издание публикации (включая любые изменения), на которую дается ссылка:
ISO/TS 16610-1:2006 Geometrical product specifications (GPS). Filtration. Part 1. Overview and basic concepts [Геометрические характеристики изделий (ГХИ). Фильтрация. Часть 1. Обзор и основные понятия]
ISO/TS 16610-20:2006 Geometrical product specifications (GPS) — Filtration — Part 20: Linear profile filters: Basic concepts [Геометрические характеристики изделий (ГХИ). Фильтрация. Часть 20. Фильтры линейного профиля. Основные понятия]
ISO/IEC Guide 98-3:2008 Uncertainty of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM: 1995) [Руководство 98-3:2008 Неопределенность измерений. Часть 3. Руководство по выражению неопределенности измерений (GUM: 1995)]
ISO/IEC Guide 99:2007 International vocabulary of metrology — Basic and general concepts and associated terms (VIM) [Международный словарь по метрологии. Основные и общие понятия и соответствующие термины (VIM)]
Издание официальное
3 Термины и определения
В настоящем стандарте применены термины по ИСО/ТС 16610-1, ИСО/ТС 16610-20, ИСО/МЭК Руководство 98-3 и ИСО/МЭК Руководство 99 и следующие термины с соответствующими определениями:
3.1
линейные фильтры профиля (linear profile filters): Фильтр профиля, используемый для разделения профиля на длинноволновый (низкочастотный) и кратковолновый (высокочастотный) компоненты.
[ISO/TS 16610-20:2006]
3.1.1
открытый профиль (open profile): Незамкнутый профиль поверхности конечной длины, включающий две конечные точки.
[ISO/TS 16610-1:2006]
3.1.2
замкнутый профиль (closed profile): Замкнутый профиль поверхности конечной длины, без конечных точек.
[ISO/TS 16610-1:2006]
3.1.3
длина волны среза (cut-off wavelength): Длина волны (период) профиля поверхности в виде синусоиды, для которого фильтр профиля пропускает 50 % амплитуды.
[\SOfTS 16610-20:2006]
4 Характеристики Гауссова фильтра профиля для открытого профиля
4.1 Гауссова весовая функция для открытого профиля
Весовая функция отрытого фильтра профиля (1) имеет вид Гауссовой функции с длиной волны среза где «с» означает «срез».
Уравнение имеет следующий вид:
s(x)
а - X,
|
exp |
|
(1)
где х — расстояние от центра (максимума) весовой функции;
Хс — длина волны среза;
а — константа для обеспечения пропускания 50 % амплитуды на длине волны среза Хц. На практике весовая функция может быть записана следующим образом:
s(x) = -А- ехр
а-Хс
2
-Хс
0 — в остальных случаях,
при -L ■ \ <x<Lc-Xc,
(2)
где Lc — константа среза весовой функции (в приложении А приведены рекомендованные значения); а — константа, равная:
а =
0,4697.
(3)
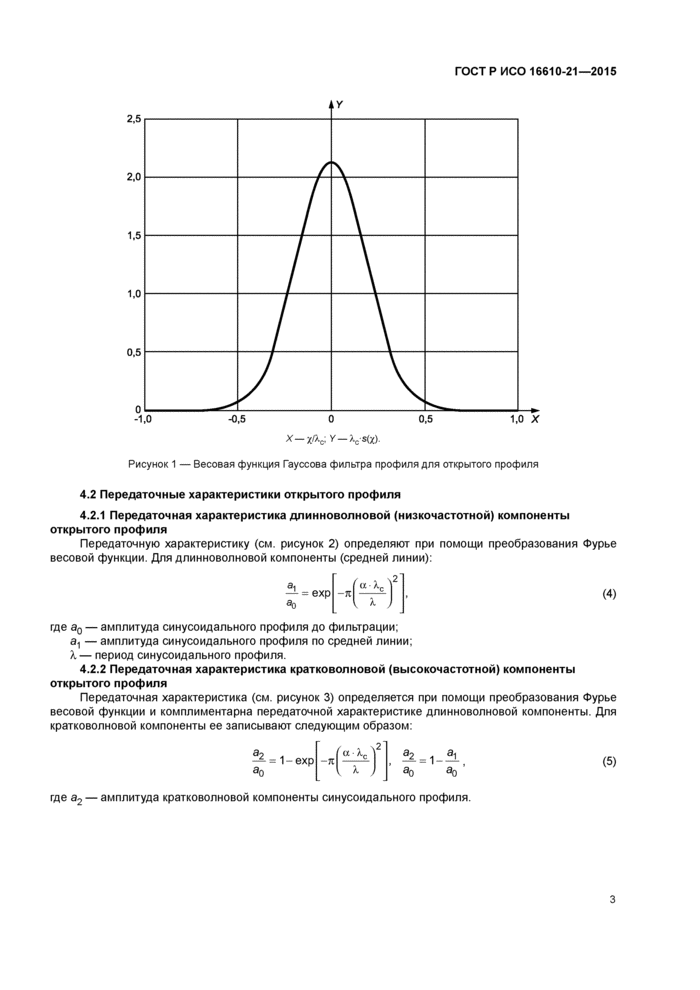
Г рафик весовой функции представлен на рисунке 1.
|
х—х\\ у-^с-$(х) Рисунок 1 — Весовая функция Гауссова фильтра профиля для открытого профиля |
4.2 Передаточные характеристики открытого профиля4.2.1 Передаточная характеристика длинноволновой (низкочастотной) компоненты открытого профиля
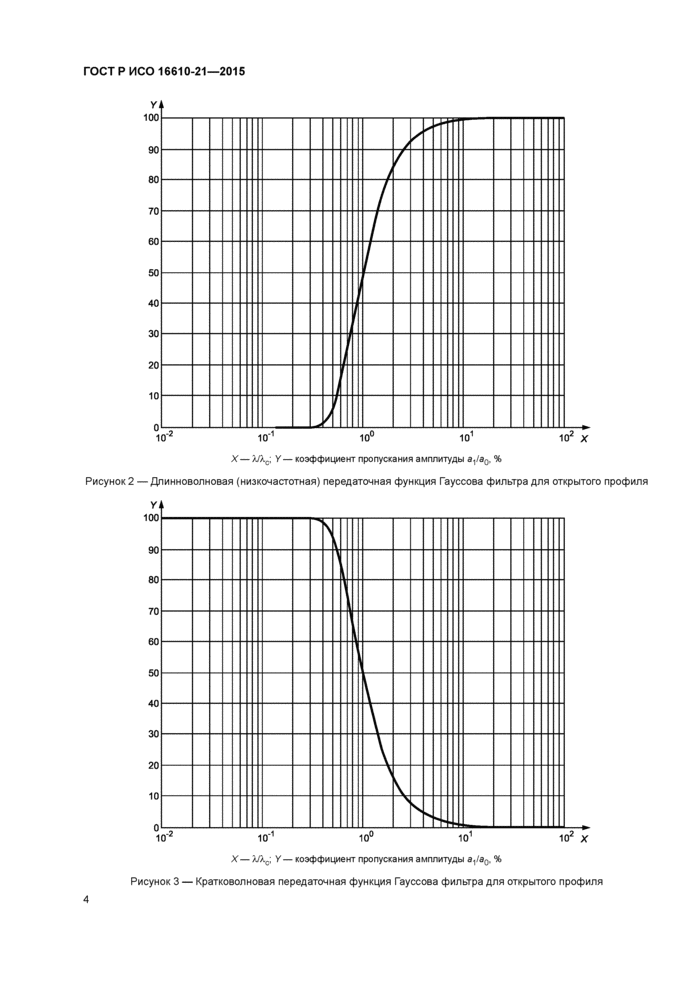
Передаточную характеристику (см. рисунок 2) определяют при помощи преобразования Фурье весовой функции. Для длинноволновой компоненты (средней линии):
^- = ехр
ао
-п
2
(4)
где а0 — амплитуда синусоидального профиля до фильтрации; а1 — амплитуда синусоидального профиля по средней линии;
X— период синусоидального профиля.
4.2.2 Передаточная характеристика кратковолновой (высокочастотной) компоненты открытого профиля
Передаточная характеристика (см. рисунок 3) определяется при помощи преобразования Фурье весовой функции и комплиментарна передаточной характеристике длинноволновой компоненты. Для кратковолновой компоненты ее записывают следующим образом:
а2
а0
1- ехр
-я
2
(5)
где а2 — амплитуда кратковолновой компоненты синусоидального профиля.
3
ГОСТ Р ИСО 16610-21-2015
X — A/Aj,; Y — коэффициент пропускания амплитуды а^Эд, %
|
Рисунок 3 — Кратковолновая передаточная функция Гауссова фильтра для открытого профиля |
Рисунок 2 — Длинноволновая (низкочастотная) передаточная функция Гауссова фильтра для открытого профиля
X — XIX ] Y — коэффициент пропускания амплитуды а^1а0, %
4