ГОСТ Р ИСО 16269-4-2017
Статистические методы. Статистическое представление данных. Часть 4. Выявление и обработка выбросов
В стандарте установлены статистические критерии и методы графического анализа данных, полученные в результате измерений. В стандарте приведены рекомендации по методам определения робастных оценок и процедурам проверки наличия выбросов в данных. Методы, представленные в стандарте, предназначены главным образом для выявления и обработки выбросов одномерных данных. Однако в стандарте представлены также некоторые рекомендации по работе с многомерными данными и данными регрессионного анализа.
Идентичен ISO 16269-4:2010
Оглавление
1 Область применения
2 Термины и определения
3 Обозначения
4 Выбросы в одномерных данных
5 Коррекция влияния выбросов в одномерной выборке
6 Выбросы многомерных и регрессионных наборов данных
Приложение А (обязательное) Алгоритм GESD-процедуры обнаружения выбросов
Приложение В (обязательное) Критические значения статистик для критерия наличия выбросов в выборке из экспоненциального распределения
Приложение С (обязательное) Значения коэффициентов модифицированной диаграммы ящик с усами
Приложение D (обязательное) Значения коэффициентов коррекции для определения робастной оценки параметра масштаба
Приложение E (справочное) Критические значения статистики критерия Кохрена
Приложение F (обязательное) Руководство по выявлению выбросов в одномерной выборке
Библиография
53 страницы
| Дата введения | 01.12.2018 |
|---|---|
| Добавлен в базу | 01.01.2018 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Строительство
- Раздел Экология
Организации:
| 10.08.2017 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 865-ст |
|---|---|---|---|
| Разработан | АО НИЦ КД | ||
| Издан | Стандартинформ | 2017 г. |
Statistical methods. Statistical data presentation. Part 4. Detection and treatment of outliers
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7
стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13
стр. 14

стр. 15

стр. 16
стр. 17

стр. 18
стр. 19

стр. 20
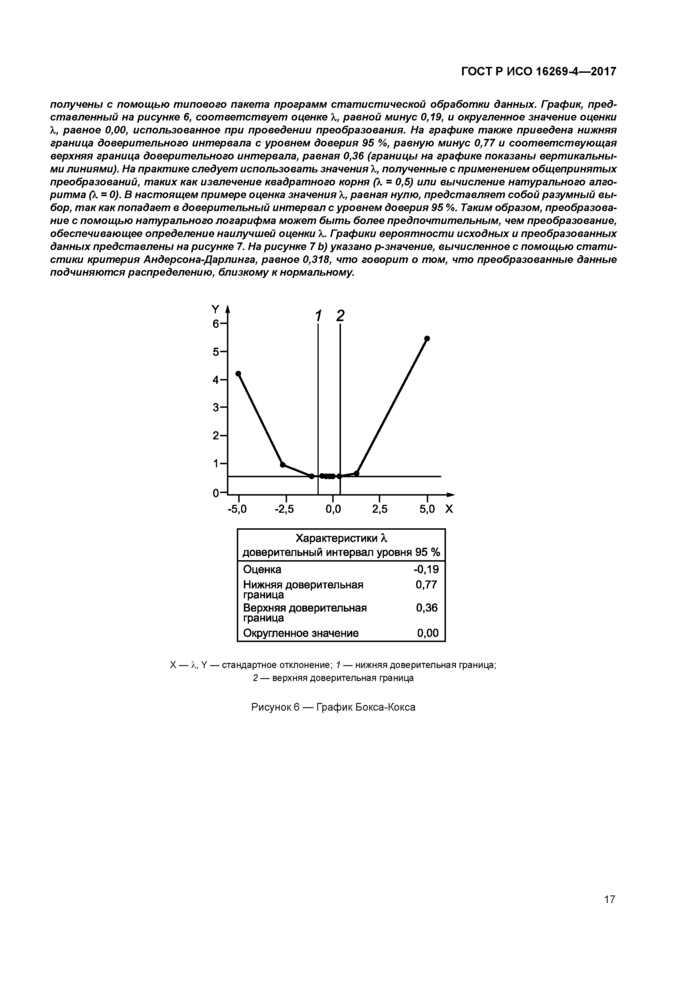
стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26
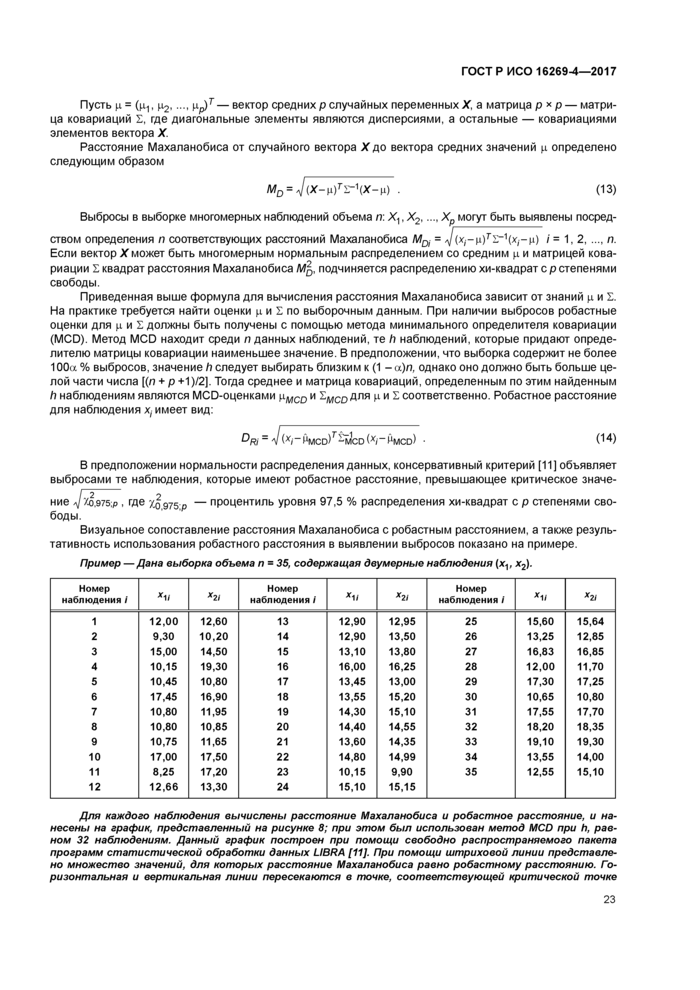
стр. 27
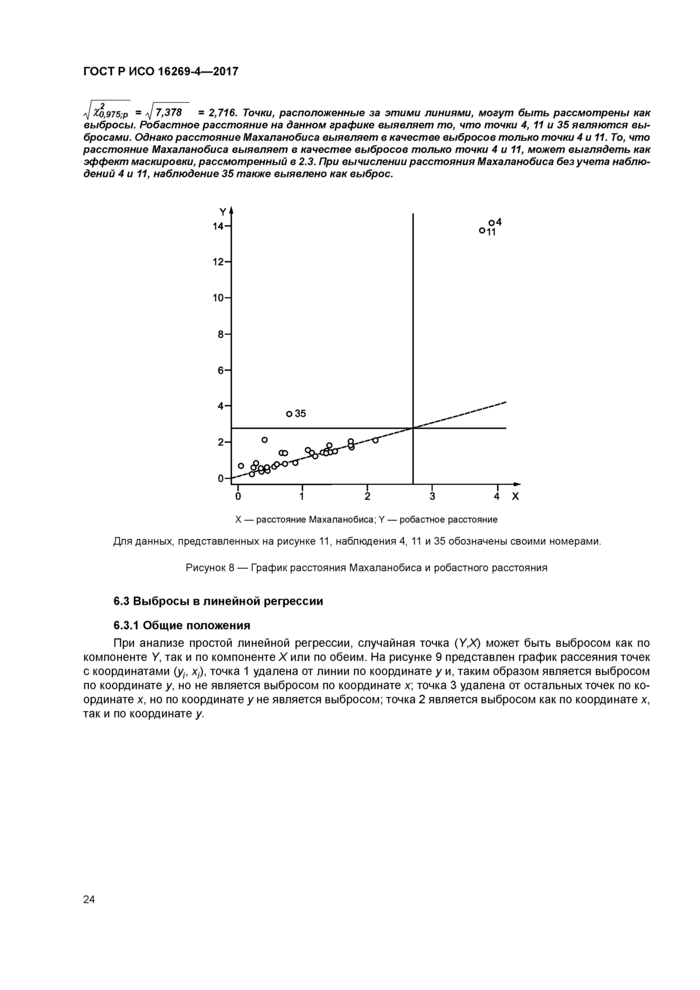
стр. 28
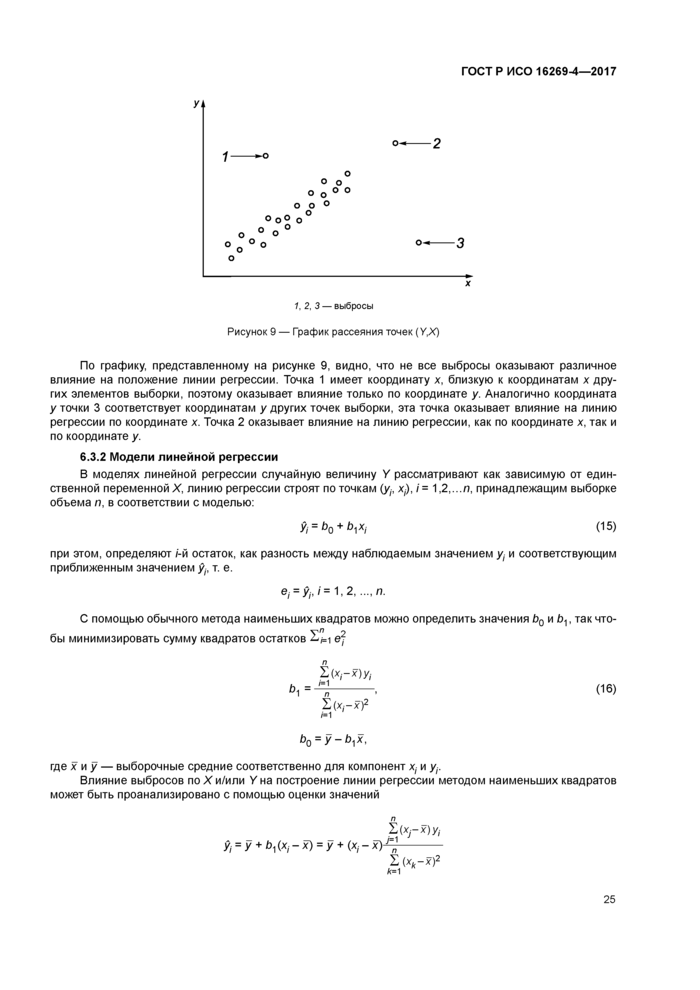
стр. 29

стр. 30
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
НАЦИОНАЛЬНЫЙ
СТАНДАРТ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ГОСТРИСО 16269-4-2017
2017
Статистические методы СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХЧасть 4Выявление и обработка выбросов
Выявление и обработка выбросов
(ISO 16269-4:2010, Statistical interpretation of data — Part 4: Detection and treatment of outliers, IDT)
Издание официальное
Москва
Стандартинформ
2017
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом аНаучно-исследовательский центр контроля и диагностики технических систем» (АО «НИЦ КД») на основе собственного перевода на русский язык англоязычной версии международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Применение статистических методов»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 10 августа 2017 г № 865-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 16269-4:2010 «Статистическое представление данных. Часть 4 Выявление и обработка выбросов» (ISO 16269-4:2010 «Statistical interpretation of data — Part 4: Detection and treatment of outliers». IDT).
Международный стандарт разработан Техническим комитетом ISO/TC 69.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г № 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты» В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (wmv.gost.ru)
© Стандартинформ. 2017
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
II
Примечание 1 — Экспоненциальное распределение является основополагающим при исследовании безотказности в ситуациях отсутствия старения или «памяти».
Примечание 2 — Математическое ожидание экспоненциального распределения равно р. Дисперсия экспоненциального распределения равна р2
Примечание 3 — Выборка экспоненциального распределения является случайной выборкой (2 1), отобранной из генеральной совокупности, подчиняющейся экспоненциальному распределению
2.25 распределение Вейбулла, распределение экстремальных значений типа III (Weibull distribution, type III extreme-value distribution): Распределение непрерывной случайной величины с функцией распределения
|
F(x) = 1 - exp |
где х — переменная, х > 0; 0. р. к — параметры -оо < 0 < <х>, |) > 0, к > 0.
(ISO 3534-1:2006. п. 2.63]
Примечание 1 — Помимо того, что распределение Вейбулла является одним из трех возможных предельных распределений экстремальных значений порядковых статистик, оно также имеет ряд других важных применений, особенно в теории надежности и инженерии Существует много ситуаций, когда полученные данные могут быть описаны распределением Вейбулла
Примечание 2 — Параметр 0 является параметром положения или пороговым параметром, это минимальное значение, которое может принимать случайная величина Параметр (I — параметр масштаба (связан со стандартным отклонением случайной величины). Параметр Л — параметр формы.
Примечание 3 — Выборка из распределения Вейбулла является случайной выборкой (2.1). отобранной из генеральной совокупности, подчиняющейся распределению Вейбулла
2.26 логнормальное распределение (lognormal distribution): Распределение случайной величины с функцией плотности вероятностей
где х — переменная, х > 0; ц, о — параметры -ж<ц<зсиа>0.
(ИСО 3534-1:2006, л. 2.52]
2.27 распределение экстремальных значений типа I, распределение Гумбеля (type I extreme-value distribution. Gumbel distribution): Распределение случайной величины с функцией распределения
F(x) = ех
гдех — переменная.х>0; ц.о — параметры-х<ц<ссио>0.
Примечание — Распределения экстремальных значений позволяют получить соответствующие распределения для экстремальных порядковых статистик (2.10) х(1) и х(п).
(ISO 3534-1:2006, п. 2.61]
3 Обозначения
В настоящем стандарте использованы следующие обозначения и сокращения:
GESD — обобщенное экстремальное стьюдентизированное отклонение:
Ge —статистика Гринвуда;
дЕ п — критическое значение статистики критерия Гринвуда для объема выборки л;
I, — редуцированная выборка объема п - /, полученная после удаления из исходной выборки /0 объема п. самого экстремального элемента х<°). затем удаления самого экстремального элемента х<1) из редуцированной выборки /, объема л - 1, удаления самого экстремального элемента х<М) из редуцированной выборки 'м объема п - / ♦ 1;
Fp у — лроцентиль F-распределения уровня р с v, и v2 степенями свободы;
— критическое значение статистики GESD—критерия при проверке того, что № является выбросом;
7
нижняя граница модифицированной диаграммы ящик с усами; верхняя граница модифицированной диаграммы ящик с усами; выборочная медиана;
h -
Мили 02 — **ad -
О, “
Оз -
R,
«(//) -
тм -
Тп -
П° -
медиана абсолютного отклонения от медианы; первый квартиль; третий квартиль.
контрольная статистика критерия GESD при проверке того, что является выбросом;
стандартное отклонение, вычисленное по редуцированной выборке /,;
медиана:
"К-1 */ —
х<'> -
Щ) -
хт(и) —
xL.n -
xUn ~
дважды взвешенная оценка параметра положения для выборки объема л; оценка Тп в /-й итерации, при объеме выборки, равном л; перцентиль уровня pt — распределения с v степенями свободы: перцентиль уровня р распределения хи-квадрат с v степенями свободы:
/-й элемент в упорядоченном наборе данных; наиболее экстремальное значение редуцированной выборки /,; выборочное среднее редуцированной выборки If а — усеченное среднее;
нижняя четверть диаграммы ящик с усами, построенной по выборке объема л; верхняя четверть диаграммы ящик с усами, построенной по выборке объема л.
4 Выбросы в одномерных данных
4.1 Общие положения
4.1.1 Понятие выброса
В простейшем случае выброс представляет собой наблюдение, несовместимое с остальными наблюдениями набора данных. В общем случае набор данных может содержать более одного выброса, расположенных, как с одной, так и с двух сторон упорядоченного набора данных. Основная проблема выявления выбросов состоит в определении того, действительно ли наблюдения, не совместимые с остальными данными являются выбросами. Эту задачу решают посредством заданного критерия значимости с учетом предполагаемого распределения данных. Наблюдения, для которых получены значимые результаты, рассматривают как выбросы из предполагаемого распределения.
Важность правильного выбора соответствующего распределения данных нельзя переоценить. На практике часто в качестве распределения данных часто рассматривают нормальное распределение, даже если данные получены из другого источника. Однако ошибочное предположение о распределении данных может приводить к некорректному отнесению элементов выборки к выбросам.
4.1.2 Причины выбросов
Появление выбросов обычно связано с одной или несколькими причинами (детальное рассмотрение приведено в (9J).
a) Ошибки измерений и регистрации данных. Сюда относят ошибки в точности измерений, некорректно проведенные наблюдения, некорректную регистрацию данных или их введения в базу данных.
b) Загрязнение данных. Загрязнения данных происходит в том случае, когда данные принадлежат двум или более распределениям, т. е. имеется одно основное распределение и одно или несколько дополнительных распределений (примесей), загрязняющих данные. Если загрязняющие распределения имеют значительно отличающиеся от основного истинные средние, большие значения стандартных отклонений и/или более тяжелые хвосты распределений, чем у основного распределения, то существует возможность того, что экстремальные наблюдения, принадлежащие распределениям-примесям, могут появиться как выбросы основного распределения.
Примечание 1 — Причиной загрязнения может быть ошибка при отборе выборки, когда небольшую часть данных считают полученной из другой совокупности или если было осуществлено преднамеренное искажение (завышение или занижение) результатов эксперимента или опроса
8
c) Ошибочное предположение о распределении данных. Набор данных считают полученным из конкретного распределения, но он получен из другого распределения.
Пример — Набор данных считают отобранным из нормального распределения, но он может иметь сильно ассимотричноо распродолонио (напримор, экспоненциальное или логнормальное) или быть симметричным, но иметь тяжелые хоосты (например, t-распределение). Поэтому наблюдения, далеко отстоящие от медианы распределения, могут быть ошибочно приняты за выбросы, даже если это достоверные данные, принадлежащие ассиметричному распределению или распределению с тяжелыми хвостами.
d) Редкие наблюдения. В выборках, отобранных (как предполагается) из заданных распределений маловероятные наблюдения могут появиться в очень редких случаях. Экстремальные наблюдения в этом случае обычно принимают за выбросы, но они не являются выбросами.
Примечание 2 — Если генеральная совокупность имеет симметричное распределение с тяжелыми хвостами, то редко поступающие наблюдения могут приводить к ошибочным предположениям о распределении
4.1.3 Необходимость обнаружения выбросов
Выбросы не всегда являются «плохими» или «ошибочными» данными. Они могут быть рассмотрены как индикаторы проявления редких явлений, требующих дальнейшего изучения. Например, если выброс вызван исключительно особенностями промышленной обработки, то важное значение имеет изучение причин выброса.
Многие методы статистической обработки данных и многие получаемые статистики чувствительны к наличию выбросов Например, выборочные среднее и стандартное отклонения могут изменить свои значения при наличии даже одного выброса, что впоследствии может привести к неверным выводам.
4.2 Проверка данных
Проверку данных начинают с простого визуального контроля полученного набора данных. Для этого строят простые графики, такие как: точечная диаграмма, диаграмма рассеяния, гистограмма, диаграмма стебель—листья, график вероятности, диаграмма ящик с усами; график данных о времени или в порядке не убывания значений. Это может привести к обнаружению новых источников изменчивости и появлению экстремальных значений в наборе данных. Например, бимодальное распределение данных, обнаруженное с помощью гистограммы или диаграммы стебель—листья, может свидетельствовать о загрязнении выборки или смеси данных из двух разных совокупностей. График вероятности и диаграмму ящик с усами рекомендуется использовать для идентификации выбросов Эти выбросы в дальнейшем необходимо исследовать с помощью методов, представленных в 4 3 или 4 4.
График вероятности позволяет не только осуществлять графическую проверку соответствия наблюдений или большей части наблюдений предполагаемому распределению, но может быть использован для выявления выбросов в наборе данных. Точки на графике вероятности, заметно отклоняющиеся от прямой, вокруг которой лежат все остальные наблюдения, следует рассматривать как возможные выбросы. Графики вероятности используют во многих пакетах программ статистического анализа данных.
Диаграмма ящик с усами — один из наиболее популярных инструментов графического представления данных. Ее используют для определения параметров положения, рассеяния и формы распределения данных. Нижние и верхние границы диаграммы ящик с усами определяют следующим образом
нижняя граница Q1 -k(Q3- О,).
верхняя граница О, + k(Q3 - о/), (1)
где О, и03 — первый и третий квартиль выборки; к — константа.
В работе Тьюки (2) наблюдения, лежащие за пределами верхней и нижней границ, при к = 1.5 рассматривают как возможные выбросы, при к = 3 их рассматривают как явные выбросы.
Примечание 1— Вероятностная бумага для нормального, логнормального, экспоненциального распределения и распределения Вейбулла может быть загружена с интернет-ресурса http //wwwweibuil com/GPaper/ index.htm
Примечание 2 — График вероятности зависит от предположений о виде распределения генеральной совокупности Например, график вероятности для экспоненциального распределения следует использовать при наличии предположений или априорных знаний о том. что выборка отобрана из генеральной совокупности, подчиняется экспоненциальному закону.
Примечание 3 — При анализе диаграммы ящик с усами, для которой верхняя и нижняя границы определены с помощью (1), большое количество наблюдений может быть ошибочно отнесено к возможным выбросам.
если выборка получена из асимметричного распределения Данная проблема может быть устранена посредством применения модифицированной диаграммы ящик с усами (см 4 4)
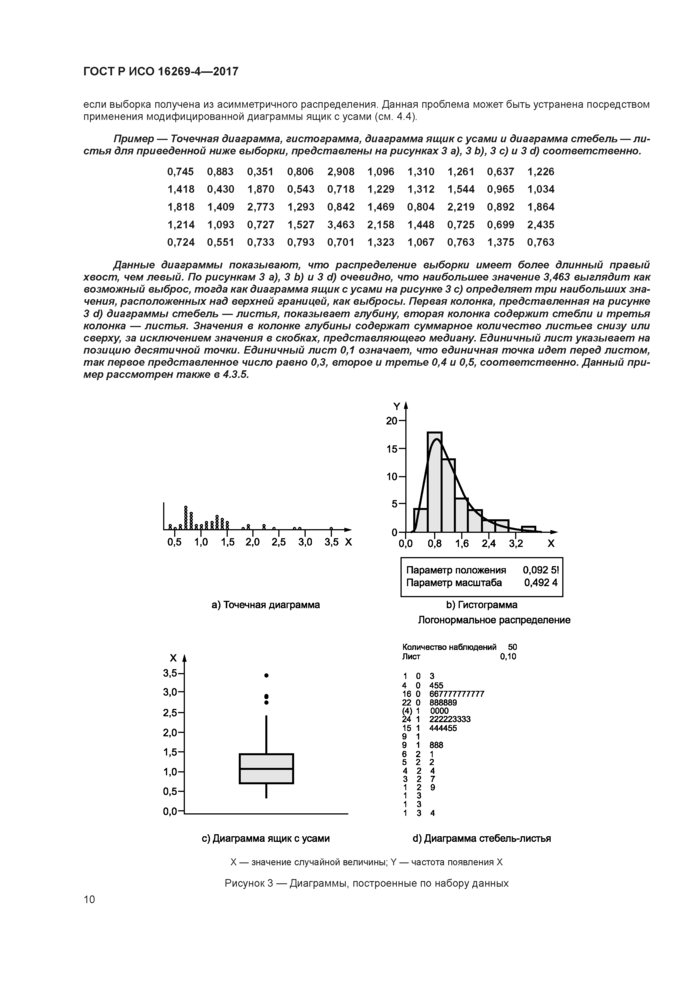
Пример — Точечная диаграмма, гистограмма, диаграмма ящик с усами и диаграмма стебель — листья для приведенной ниже выборки, представлены на рисунках 3 а), 3 Ь), 3 с) и 3 d) соответственно.
|
0.745 |
0,883 |
0.351 |
0.806 |
2,908 |
1.096 |
1.310 |
1.261 |
0.637 |
1.226 |
|
1,418 |
0.430 |
1.870 |
0.543 |
0.718 |
1.229 |
1.312 |
1,544 |
0.965 |
1.034 |
|
1,818 |
1.409 |
2.773 |
1.293 |
0.842 |
1.469 |
0,804 |
2,219 |
0.892 |
1.864 |
|
1,214 |
1.093 |
0.727 |
1,527 |
3,463 |
2.158 |
1,448 |
0.725 |
0.699 |
2.435 |
|
0.724 |
0.551 |
0.733 |
0.793 |
0.701 |
1.323 |
1.067 |
0.763 |
1.375 |
0.763 |
|
Y 20- |
Данные диаграммы показывают, что распределение выборки имеет более длинный правый хвост, чем левый. По рисункам 3 а), 3 Ь) и 3 d) очевидно, что наибольшее значение 3,463 выглядит как возможный выброс, тогда как диаграмма ящик с усами на рисунко 3 с) определяет три наибольших значения, расположенных над верхней границей, как выбросы. Первая колонка, представленная на рисунке 3 d) диаграммы стебель — листья, показывает глубину, вторая колонка содержит стебли и третья колонка — листья. Значения в колонке глубины содержат суммарное количество листьев снизу или сверху, за исключением значения в скобках, представляющего медиану. Единичный лист указывает на позицию десятичной точки. Единичный лист 0,1 означает, что единичная точка идет перед листом, так порвоо представленное число равно 0,3, второе и тротье 0.4 и 0.5. соответственно. Данный пример рассмотрен также в 4.3.5.
л t . . t
| ||||
|
Ь) Гистограмма Логонормальное распределение |
0.5 1.0 1.5 2.0 2.5 3.0 3.5 X
а) Точечная диаграмма
|
Количество наблюдений 50 | |||||||||||||||||||||||||||
|
с) Диаграмма ящик с усами d) Диаграмма стебель-листья
X — значение случайной величины; Y — частота появления X Рисунок 3 — Диаграммы, построенные по набору данных
10
4.3 Выявление выбросов
4.3.1 Общие положения
Существует большое количество методов выявления выбросов (см. (1]). В ИСО 5725-2 (см. (3]) приведены критерии Граббса и Кохрена для идентификации выбросов данных лабораторий. Критерий Грабса применим к отдельным наблюдениям или к выборочным средним наборов данных из нормальных распределений; критерий может быть использован только для выявлений двух наибольших и/или наименьших наблюдений в качестве выбросов в наборе данных. Более общая процедура анализа, представленная в 4.3.2. способна обнаруживать множественные выбросы при анализе отдельных наблюдений или средних арифметических наборов данных, отобранных из нормального распределения. Процедуры, приведенные в 4.3.3 и в 4.3.4, способны обнаруживать множественные выбросы для данных. отобранных из экспоненциального распределения, распределения экстремальных значений типа I. распределения Вейбулла или гамма-распределения. Процедуру, приведенную в 4,3.5. следует применять для обнаружения выбросов в выборках, отобранных из совокупностей с неизвестным законом распределения. Процедура обнаружения выбросов по набору дисперсий, полученных из набора выборок, приведена в 4.3.6.
4.3.2 Выборка из нормального распределения
Один или более выбросов с обеих сторон набора данных из нормального распределения могут быть выявлены при помощи процедуры, известной как обобщенное экстремальное стьюдентизирован-ное отклонение (GESD) (см. (4)). Процедура GESD пригодна для контроля ошибки первого рода при обнаружении более чем / выбросов с уровнем значимости а и 1 й I £ т. где т — установленное максимальное количество выбросов.
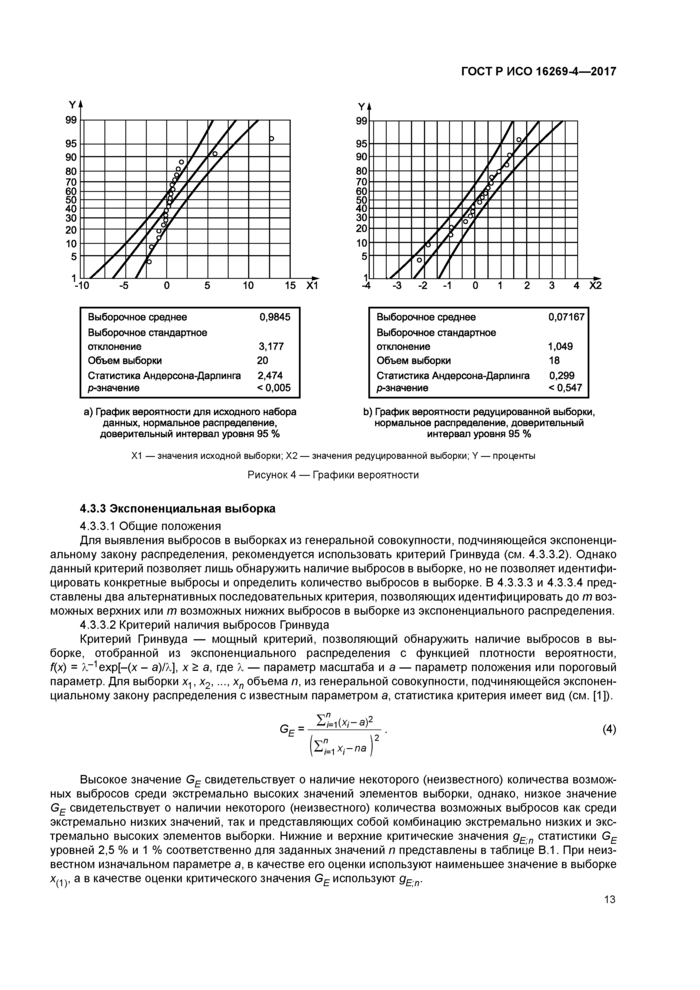
Перед применением данной процедуры следует удостовериться, что большую часть выборочных данных согласуется с нормальным распределением. График вероятности для нормального распределения. приведенный в ИСО 5479 (см. [18]). может быть использован для проверки справедливости предположения о нормальности распределения.
Этапы процедуры GESD
Этап 1. Точки, соответствующие данным выборки х,. х2 х„ наносят на график на нормальной
вероятностной бумаге. Подсчитывают количество точек, значимо отклоняющихся от прямой линии, которой соответствуют остальные точки графика. Таким образом, получают количество возможных (предполагаемых) выбросов.
Этап 2. Выбирают уровень значимости а и устанавливают количество выбросов т как число большее или равное числу возможных выбросов, полученному на шаге 1. Следующие этапы начинают, считая 1 = 0.
Этап 3. Вычисляют контрольную статистику
та.х1*-*(//)!
где
/0 — исходный набор данных;
I, — редуцированная выборка объема п - /. полученная исключением элемента выборки /м, что дает значение /?м;
Щ — выборочное среднее выборки If
s(l,) — выборочное стандартное отклонение выборки I,.
Примечание 1 — В случае 1=0 x(/q) и s(/q) — выборочное среднее и выборочное стандартное отклонение исходной выборки /0 = {х,. х2.....xj объема п. где наибольшим значением среди значений х, - х(/0),
х2 - х(/0).....х„- х-(/0) является, например, значение х2 - х(/0) далее R0 = [х2 - x(/0)J / s[l0) и х<°> = х2 Соответственно.
/, = /0 / {*«»} = (х,. Ху .... х„) — редуцированная выборка размера п - 1. полученная исключением элемента х<°>. т. е х2 из /0
Этап 4. Вычисляют критическое значение
(3)
(n-/-1)W2 V<f,-/-2*^-2><n-1> ’
11
гдер= (1 -аУ2)1«'>“'> и tp v — процентиль уровня IOOpf-распределения с \ степенями свободы. Поскольку выбросы могут быть только среди верхних или нижних экстремальных значений, а заменяют на а/2.
Этап 5. Пусть / = / +1
Этап 6. Повторяют этапы 2—4 до тех пор. пока / не станет равно т.
Этап 7. Если R, £ к, для всех / = 0.1.2 т, то считают, что выбросы не обнаружены. В противном
случае nout наиболее экстремальных наблюдений х<°\ х<,>. х<Лв*" ’> редуцированных выборок считают выбросами, при этом л.,., = 1 + max {/: R, >
OsJS/n
В приложении А приведен алгоритм программной реализации процедуры выявления выбросов GESD.
Примечание 2 — Применение процедуры GESD эквивалентно применению критерия Граббса для проверки того, является ли наибольшее или наименьшее набтодение выбросом Критические значения критерия Граббса приведены в таблице 5 ИСО 5725-2 1994 (3), они также могут быть аппроксимированы значением а, при 1 = 0 (см этап 4).
Примечание 3 — На практике, выбирают небольшое значение количества возможных выбросов т. Если в выборке ожидается наличие большого количества выбросов, то в этом случае прекращают рассматривать проблему обнаружения выбросов, и для изучения ситуации применяют другие методы Однако т не должно быть слишком маленьким, в противном случае может присутствовать эффект маскировки
Пример — Рассмотрим набор данных из 20 наблюдений:
-2,21 -1.84 -0.95 -0.91 -0,36 -0,19 -0.11 -0.10 0.18 0.30
0,43 0.51 0.64 0.67 0.93 1.22 1.35 1.73 5.80 12.6.
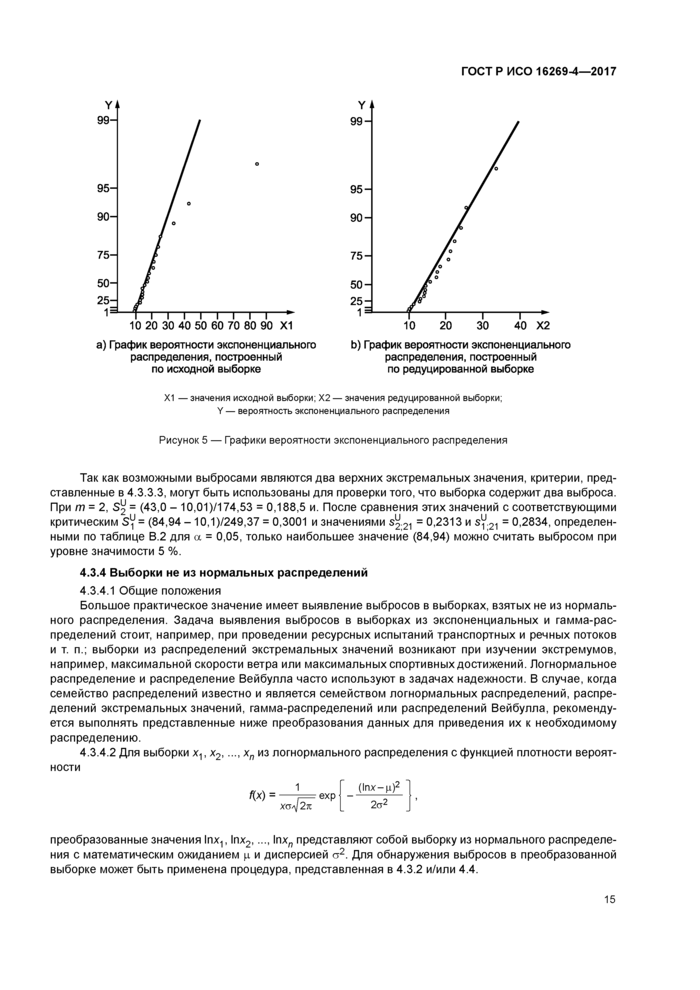
где последние два наблюдения первоначально составляли 0,58 и 1,26, но при регистрации данных запятые, отделяющие десятичные разряды, были ошибочно сдвинуты. Перед применением процедуры GESD для обнаружения выбросов необходимо проверить, что наблюдения соответствуют нормальному распределению. Точки на графике вероятности на нормальной вероятностной бумаге (см. рисунок 4 а)) расположены вблизи прямой линии, за исключением двух лючек с наибольшими значениями, заметно отклоняющихся от прямой. Данный график показывает, что набор данных, за исключением двух экстремальных значений, можно считать принадлежащим нормальной совокупности. Данное предположение подтверждает рисунок 4 Ь), где на графике вероятности все данные, за исключением двух крайних значений, расположены внутри границы с уровнем доверия 95 % доверительного интервала. Таким образом, на этапе 2 можно выбрать т * 2. Статистика критерия GESD (RJ и ее критическое значонио а, для I ■ 0,1,2 и уровня значимости a ■ 0,05 представлены ниже.
| ||||||||||||||||
|
Так как R0 = 3,6559 > Х0 = 2,7058, Я, = 3,2634 > X, = 2,6785 и R2 ■ 2,1761 £ \2 = 2,6992, следовательно, max {I: Rt>\f • 1 и n^, = 1 + max {l:Rf> « 2. Таким образом обнаружено два выброса, это два наиболее |
экстремальных значения: х№ = 12,60 и х<°) ■ 5,80.
Примечание 4 — В этом и в следующем примерах не указаны единицы, в которых выполнены измерения данных, так как они не требуются для графической интерпретации и анализа данных, проводимого в рамках настоящего стандарта
12
Содержание
1 Область применения................................................................ 1
2 Термины и определения............................................................. 1
3 Обозначения....................................................................... 7
4 Выбросы в одномерных данных....................................................... 8
5 Коррекция влияния выбросов в одномерной выборке.....................................20
6 Выбросы многомерных и регрессионных наборов данных.................................22
Приложение А (обязательное) Алгоритм GESD-процедуры обнаружения выбросов..............31
Приложение В (обязательное) Критические значения статистик для критерия наличия выбросов
в выборке из экспоненциального распределения..............................32
Приложение С (обязательное) Значения коэффициентов модифицированной диаграммы
ящик с усами............................................................38
Приложение D (обязательное) Значения коэффициентов коррекции для определения
робастной оценки параметра масштаба.....................................40
Приложение Е (справочное) Критические значения статистики критерия Кохрена................41
Приложение F (обязательное) Руководство по выявлению выбросов в одномерной выборке......45
Библиография.......................................................................47
Введение
Выявление выбросов — одна из старейших проблем анализа данных. Причинами появления выбросов могут быть ошибки измерений, ошибки отбора выборки, преднамеренное искажение или некорректная фиксация результатов анализа выборки, ошибочные предположения о распределении данных или модели, малое количество наблюдений и т. д.
Выбросы могут искажать и сокращать информацию, содержащуюся в источнике данных или процедуре их генерации. В производстве наличие выбросов снижает результативность производственных процессов, качество продукции, а также процедур контроля продукции. Выбросы не всегда следует трактовать как «плохие» или «ошибочные» данные. В некоторых случаях выбросы дают важную информацию. которую необходимо учитывать в процессе исследований.
Выявление и анализ выбросов в процессе измерения ведут к более полному пониманию изучаемых процессов и более глубокому анализу данных, и как следствие, к более достоверным выводам.
Так как проблеме обнаружения и обработки выбросов посвящено большое количество литературных публикаций, важной задачей является определение и стандартизация (на межаународном уровне) этих методов.
Настоящий стандарт содержит шесть приложений. В приложении А приведен алгоритм вычисления статистик и критических значений для выявления выбросов в выборке из нормально распределения. В приложениях В, D и Е приведены таблицы, необходимые для применения рекомендованных в стандарте процедур. В приложении С приведено статистическое обоснование построения диаграмм, помогающих в решении задачи отслеживания выбросов. В приложении F приведено поэтапное руководство по применению процедур, установленных в настоящем стандарте, и представлена блок-схема соответствующих действий.
IV
ГОСТ Р ИСО 16269-4-2017
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ Часть 4 Выявление и обработка выбросов
Statistical methods Statistical data presentation Part 4 Detection and treatment of outliers
Дата введения — 2018—12—01
1 Область применения
В настоящем стандарте установлены статистические критерии и методы графического анализа данных, полученные в результате измерений. В настоящем стандарте приведены рекомендации по методам определения робастных оценок и процедурам проверки наличия выбросов в данных.
Методы, представленные в настоящем стандарте, предназначены главным образом для выявления и обработки выбросов одномерных данных. Однако в настоящем стандарте представлены также некоторые рекомендации по работе с многомерными данными и данными регрессионного анализа.
2 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1 выборка, набор данных (sample, data set): Подмножество генеральной совокупности, состоящее из одной или нескольких выборочных единиц.
Примечание 1 — В зависимости от исследуемой генеральной совокупности выборочными единицами могут быть объекты, числовые значения, а также абстрактные элементы
Примечание 2 — Выборку из генеральной совокупности, подчиняющуюся нормальному распределению (2 22), гамма-распределению (2 23), экспоненциальному распределению (2 24), распределению Вейбулла (2 25). логнормальному распределению (2 26) или распределению экстремальных значений типа I (2 27) часто называют выборкой из нормального распределения, гамма-распределения, экспоненциального распределения, распределения Вейбулла. логнормального распределения или распределения экстремальных значений типа I соответственно
2.2 выброс (outlier): Элемент маломощного подмножества выборки, существенно отличающийся от остальных элементов выборки (2.1).
Примечание 1— Классификация наблюдения или подмножество выборки как выброс (или выбросы) зависит от выбранной модели генеральной совокупности, из которой отобрана выборка Выброс не рассматривают как истинный элемент генеральной совокупности
Примечание 2 — Выброс может появиться из другой генеральной совокупности, быть результатом некорректной регистрации данных или общей ошибкой измерений
Примечание 3 — Подмножество может содержать одно или несколько наблюдений
2.3 маскировка (masking): Наличие более одного выброса (2.2). затрудняющее обнаружение каждого выброса.
2.4 вероятность ложного обнаружения выбросов (some-outside rate): Вероятность того, что одно или несколько наблюдений незагрязненной выборки, ошибочно классифицированы как выбросы (2.2).
2.5 метод коррекции выбросов (outlier accommodation method): Метод нечувствительный к наличию выбросов (2.2) при принятии решения о генеральной совокупности.
Издание официальное
2.6 устойчивая оценка (resistant estimation): Оценка, подверженная лишь малым изменениям при замене небольшой доли набора данных (2.1). элементами, возможно, имеющими значительное отличие от замененных элементов.
2.7 робастная оценка (robust estimation): Оценка, нечувствительная к небольшим отклонениям от предполагаемой вероятностной модели данных.
Примечание — Примером может быть оценка, полученная методом, предназначенным для нормального распределения (2 2). при применении к близким распределениям, но имеющим некоторую асимметрию или тяжелые хвосты функции распределения Группа таких оценок включает в себя L-оценки (взвешенное среднее арифметическое порядковых статистик (2 10)) и М-оценки (см (9))
2.8 ранг (rank): Положение наблюдаемого значения в упорядоченном наборе наблюдаемых значений.
Примечание 1— Наблюдаемые значения упорядочивают в неубывающем (ведя отсчет от наименьшего элемента) или в невозрастающем (ведя отсчет от наибольшего элемента) порядке
Примечание 2 — В соответствии с целями настоящего стандарта одинаковым наблюдаемым значениям присваивают разные, но последовательные ранги
2.9 глубина (depth): Наименьший из двух рангов (2.8), присвоенных элементу при упорядочивании выборки (2.1) в неубывающем и невозрастающем порядках.
Примечание 1 — Значение глубины может быть не целым числом (см приложение А).
Примечание 2 — Для всех полученных значений, отличных от медианы (2.11), глубина определяет два значения — одно ниже медианы, другое выше медианы Например, два значения с глубиной 1 представляют собой минимальное и максимальное значение в выборке (2.1).
2.10 порядковая статистика (order statistic): Статистика, определяемая рангом при упорядочивании набора данных в неубывающем порядке.
(ИСО 3534-1:2006. п. 1.9]
Примечание 1 — Пусть (х,. х2. ... х„} — неупорядоченная выборка После ее упорядочивания, обозначенные заново элементы составляют упорядоченную выборку, где х(1) £ x^ s £ х^ £... £ x(rt). тогда х(Д) — наблюдаемое значение к-й порядковой статистики в выборке объема п
Примечание 2 — На практике для определения порядковых статистик данных в выборке (2 1) производят их упорядочивание в соответствии с примечанием 1.
п * 1
of a set of numbers. 02): /с-я порядковая статистика, где к = —z— .
Г л “I . Гл+1
число или полусумма — -й и —— -и порядковых статистик.
2.11 медиана, выборочная медиана, медиана набора чисел 02 (median, sample median, median
если объем выборки — нечетное если л — четное число.
(ИСО 3534-1:2006, п. 1.13)
Примечание — Медиана является вторым квартилем (Q2)
2.12 первый квартиль, нижний выборочный квартиль Q, (first quartile sample lower quartile. О,): Медиана (2.11) первых наименьших (л —1)/2 значений для нечетного числа наблюдений; медиана первых наименьших л/2 значений для четного числа наблюдений.
Примечание 1 — В литературе встречается много различных определений выборочного квартиля, что приводит в некоторой степени к различным выводам В настоящем стандарте приведено определение, которое широко распространено и удобно в применении
Примечание 2 — Популярными вариантами квартиля являются «сгибы» и «четверти* (2 19 и 2 20) В некоторых случаях (см примечание 3 в 2 19) первый квартиль и нижняя четверть (2 19) идентичны
2.13 третий квартиль, верхний выборочный квартиль Q3 (third quartile, sample upper quartile, O3): Медиана (2.11) последних наибольших (л — 1)/2 значений для нечетного числа наблюдений или медиана последних наибольших л/2 значений для четного числа наблюдений.
Примечание 1—В литературе встречается много различных определений выборочного квартиля, что приводит в некоторой степени к различным выводам В настоящем стандарте приведено определение, которое широко распространено и удобно в применении
Примечание 2 — Популярными вариантами квартиля являются «сгибы» и «четверти* (2 19 и 2 20) В некоторых случаях (см примечание 3 в 2 20) третий квартиль и верхняя четверть (2 20) идентичны
2
2.14 межквартильный размах IQR (interquartile range. IQR): Разность третьего квартиля (2.13) и первого квартиля (2.12).
Примечание 1 — Межквартильный размах — широко применяемая статистика для описания рассеяния данных
Примечание 2 — Иногда вместо межквартильного размаха используют разность верхней четверти (2 20) и нижней четверти (2 19), называемую «четвертным разбросом*
2.15 сводка пяти чисел (five-number summary): Набор значений выборочного минимума, первого квартиля (2.12). медианы (2.11). третьего квартиля (2.13) и выборочного максимума.
Примечание — Сводка пяти чисел дает краткую количественную информацию о положении, рассеянии и размахе данных
2.16 диаграмма ящик с усами (box plot): Графическое представление (горизонтальное или вертикальное) сводки пяти чисел (2.15).
Примечание 1 — В случае горизонтального представления диаграммы ящик с усами, первый квартиль (2 12) и третий квартиль (2.13) наносят на диаграмму как левую и правую боковые стороны ящика, медиану (2.11) наносят как вертикальную линию, перерезающую ящик, левый ус идет от первого квартиля к наименьшему значению в выборке, не выходящему за нижнюю границу (2 17), правый ус идет от третьего квартиля к наибольшему значению, не выходящему за верхнюю границу (2 18). значения за пределами контрольных границ рассматривают как выбросы В случае вертикального представления диаграммы, первый и третий квартили наносят на диаграмму, как нижнюю и верхнюю стороны ящика, медиану наносят как горизонтальную линию, перерезающую ящик, нижний ус идет от первого квартиля к наименьшему значению в выборке, не выходящему за нижнюю границу, верхний ус идет от третьего квартиля к наибольшему значению, не выходящему за верхнюю границу, значения за пределами контрольных границ рассматривают как выбросы
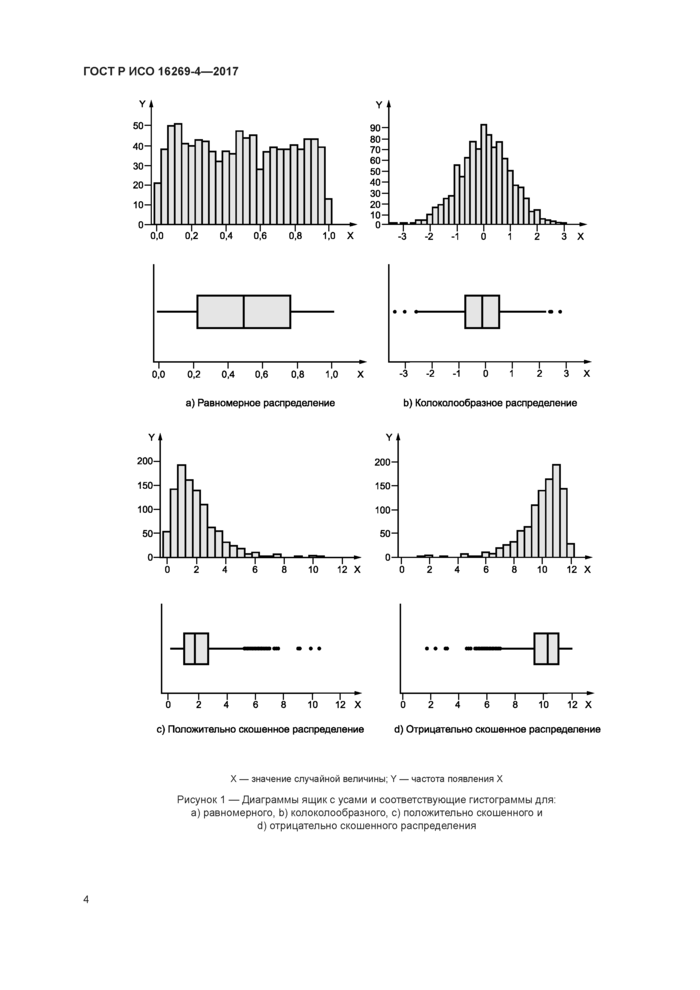
Примечание 2 — Ширина ящика и длина уса — графические параметры диаграммы, характеризующие данные, например, параметр положения, разброс, асимметрию, длину хвостов и выбросы На рисунке 1 для сравнения представлена диаграмма ящик с усами и функция плотности для а) равномерного. Ь) колоколообразного, с) положительно скошенного и d) отрицательно скошенного распределений Для каждого распределения над диаграммой ящик с усами приведена соответствующая гистограмма
Примечание 3 —Диаграмму ящик с усами с нижней (2 17) и верхней (2 18) границами, вычисленными с использованием коэффициента к. рассчитанного на основе объема выборки л и предположении о виде распределения данных, называют модифицированной диаграммой ящик с усами (см рисунок 2) Построение модифицированной диаграммы ящик с усами представлено в 4 4
2.17 нижняя граница, нижняя граница отделяющая выбросы, нижнее предельное значение
(lower fence, lower outlier cut-off. lower adjacent value): Значение, указанное на диаграмме ящик с усами (2.16). находящееся ниже первого квартиля (2.12) на заданное число к межхвартильных размахов (2.14).
Примечание — В специализированных пакетах программ статистической обработки данных нижнюю границу обычно вычисляют как Q, - /с(03 - О,), где к берут равным 1.5 или 3,0 В классическом подходе, при к - 1.5 нижнюю границу называют «внутренней нижней границей*, а при к = 3.0 нижнюю границу называют «внешней нижней границей».
3
Т-1-1-1-1-1 —I-1-1-1-1-1—I—
0,0 0.2 0.4 0.6 0.8 1.0 X -3 -2 -1 0 1 2 3 X
а) Равномерное распределение Ь) Колоколообразное распределение
с) Положительно скошенное распределение d) Отрицательно скошенное распределение
X — значение случайной величины; Y — частота появления X
Рисунок 1 —Диаграммы ящик с усами и соответствующие гистограммы для а) равномерного, Ь) колоколообразного, с) положительно скошенного и d) отрицательно скошенного распределения
4
Максимальное выборочное значение
т
1.5 х IQR
Верхняя граница (нарисована пунктиром)
Максимальное выборочное значение, расположенное ниже верхней границы
Третий квартиль
Медиана Первый квартиль
Минимальное выборочное значение, расположенное выше нижней границы
Нижняя граница (нарисована пунктиром)
Рисунок 2 — Модифицированная диаграмма ящик с усами с указанными нижней и верхней границами
2.18 верхняя граница, верхняя граница отделяющая выбросы, верхнее предельное значение
(upper fence, upper outlier cut-off. upper adjacent value): Значение, указанное на диаграмме ящик с усами, расположенное выше третьего квартиля (2.13) на заданное число к межхвартильных размахов (2.14).
Примечание — В специализированных пакетах программ статистической обработки данных верхнюю границу обычно вычисляют как Q, ♦ *(Q3 - Q,). где к берут равным 1,5 или 3.0 В классическом подходе, при к = 1,5 верхнюю границу называют «внутренней верхней границей», а при к = 3,0 верхнюю границу называют «внешней верхней границей»
2.19 нижняя четверть xL:n (lower fourth. xL п): Для набора наблюдаемых значений х^ 5 ... 5 х,л) величина, равная 0.5(х^ + х(/>1)) при 7= 0 или х^ при f> 0, где /—целая часть л/4, a f— дробная часть п! 4
Примечание 1 —Данное определение нижней четверти используют для вычисления рекомендуемых значений kL и ки (см приложение С); во многих программных продуктах статистической обработки данных вычисление нижней четверти по умолчанию или в качестве выбираемой опции производится так. как указано в определении Примечание 2 — Нижнюю четверть и верхнюю четверть (2 20) вместе иногда называют сгибами Примечание 3 — Нижнюю четверть иногда рассматривают как первый квартиль (2 12) Примечание 4 — При 1 = 0.1 - 0.5 или f = 0.75 нижняя четверть тождественно равна первому квартилю, например
|
Объем выборки л |
i ■ целая часть л/4 |
t * дробная часть л/4 |
Первый квартиль |
Нижняя четверть |
|
9 |
2 |
0,25 |
1х(2) + х(зУ2 |
ж(3) |
|
10 |
2 |
0.50 |
х(3> |
х(3) |
|
11 |
2 |
0.75 |
х(3> |
х(3) |
|
12 |
3 |
0 |
1х(3) * х(4>У2 |
tx(3) * х(4)У2 |
5
2.20 верхняя четверть Хц.п (lower fourth. хУл): Для набора наблюдаемых значений ... £ х(п)
величина, равная 0.5[x(rw) + х(гыИ)] при Г - 0 или х(М при 1> 0. где / — целая часть л/4. a /— дробная часть л/4.
Примечание 1 — Данное определение верхней четверти используют для вычисления рекомендуемых значений ки и kL (см. приложение С); во многих программных продуктах статистической обработки данных вычисление верхней четверти по умолчанию или в качестве выбираемой опции производится так. как указано в определении Примечание 2 — Нижнюю четверть (2 19) и верхнюю четверть вместе иногда называют сгибами Примечание 3 — Верхнюю четверть иногда рассматривают как третий квартиль (2 13) Примечание 4 — При / = 0. / = 0.5 или /=0,75 верхняя четверть тождественно равна третьему квартилю, например
|
Объем выборки п |
I« целая часть п/4 |
/ = дробная часть п/4 |
Третий квартиль |
Верхняя четверть |
|
9 |
2 |
0.25 |
(*(7> + *<№ |
*<7> |
|
10 |
2 |
0.50 |
*(3> |
*(в) |
|
11 |
2 |
0.75 |
*(в) | |
|
12 |
3 |
0 |
1х(9) + X,10)V2 |
[*(9) * x(io>V2 |
2.21 ошибка первого рода (Type I error): Отклонение нулевой гипотезы, когда она истинна.
[ISO 3534-1 2006. п. 1 46]
Примечание 1— Ошибка первого рода — это принятие неверного решения Поэтому, желательно поддерживать вероятность принятия такого ошибочного решения была столь малой, насколько это возможно
Примечание 2 — Возможно в некоторых ситуациях (например, при определении параметра биномиального распределения р), заданный уровень значимости, например. 0,05, не достижим для дискретных данных
~(х—и)2
2о2
2.22 нормальное распределение, распределение Гаусса (normal distribution. Gaussian distribution): Распределение непрерывной случайной величины с функцией плотности вероятностей
f{x) * —= exp <т^2 т.
где х — переменная -х < х < ж; ц, а — параметры -» < ц < *, а > 0.
[ISO 3534-1:2006, п. 2.50)
Примечание 1 — Математическое ожидание ц — параметр положения, стандартное отклонение <т — параметр рассеяния данных
Примечание 2 — Нормальная выборка является случайной выборкой (2 1). отобранной из генеральной совокупности, подчиняющейся нормальному распределению
2.23 гамма-распределение (gamma distribution): Распределение непрерывной случайной величины с функцией плотности вероятностей
^«ФНг/W
РвП«)
где х — переменная, х > 0; а, р — параметры, а > 0. р > 0.
[ISO 3534-1:2006. п. 2.56]
Примечание 1 — Гамма-распределение используют при исследовании безотказности для моделирования наработки до отказа Оно включает экспоненциальное распределение (2 24), а также другие распределения, у которых интенсивность отказов увеличивается во времени
Примечание 2 — Математическое ожидание гамма-распределения равно <ф. дисперсия равна up2 Примечание 3 — Выборка гамма-распределения является случайной выборкой (2.1), отобранной из генеральной совокупности, подчиняющейся гамма-распределению
2.24 экспоненциальное распределение (exponential distribution): Распределение непрерывной случайной величины с функцией плотности вероятностей
Дх) = р-’ехрЬх/р).
где х — переменная, х > 0; р — параметр, р > 0.
[ISO 3534-1:2006. п. 2.58]