ГОСТ Р ИСО 11843-5-2012
Статистические методы. Способность обнаружения. Часть 5. Методология в случаях линейной и нелинейной калибровки
В стандарте рассмотрены линейные и нелинейные функции калибровки и установлены основные методы:
- построения функции прецизионности отклика, а именно, описания стандартного отклонения (SD) или коэффициента вариации (СV) отклика как функции приведенной переменной состояния;
- преобразования функции прецизионности в аналогичную функцию для приведенной переменной состояния и функции калибровки;
- использования полученной функции для оценки критического значения и минимального обнаруживаемого значения приведенной переменной состояния.
Методы, приведенные в стандарте, применимы, например, для проверки обнаружения какого-либо вещества различным измерительным оборудованием, к которому не может быть применен ИСО 11843-2.
В стандарте расширены методы, приведенные в ИСО 11843-2, на случай нелинейной калибровки.
В стандарте рассмотрены случаи, когда стандартное отклонение или коэффициент вариации известны только в окрестности минимального обнаруживаемого значения.
Идентичен ISO 11843-5:2008
Переиздание. Март 2019 г.
Оглавление
1 Область применения
2 Нормативные ссылки
3 Термины и определения
4 Функция прецизионности приведенной переменной состояния
5 Критическое значение и минимальное обнаруживаемое значение приведенной переменной состояния
6 Примеры
Приложение A (обязательное) Условные обозначения и сокращения, используемые в настоящем стандарте
Приложение B (справочное) Обоснование уравнения (9)
Приложение C (справочное) Обоснование уравнения (13)
Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов национальным стандартам
Библиография
20 страниц
| Дата введения | 01.12.2013 |
|---|---|
| Добавлен в базу | 01.10.2014 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Строительство
- Раздел Экология
- Раздел Электроэнергия
- Раздел Строительство
- Раздел Экология
Организации:
| 29.11.2012 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 1420--ст |
|---|---|---|---|
| Разработан | АНО НИЦ КД | ||
| Издан | Стандартинформ | 2014 г. | |
| Издан | Стандартинформ | 2019 г. |
Statistical methods. Capability of detection. Part 5. Methodology in the linear and non-linear calibration cases
- ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
- ГОСТ Р ИСО 11843-1-2007 Статистические методы. Способность обнаружения. Часть 1. Термины и определения
- ГОСТ Р ИСО 11843-2-2007 Статистические методы. Способность обнаружения. Часть 2. Методология в случае линейной калибровки
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6
стр. 7
стр. 8

стр. 9

стр. 10
стр. 11
стр. 12
стр. 13

стр. 14

стр. 15

стр. 16
стр. 17

стр. 18

стр. 19

стр. 20
ГОСТ Р исо 11843-5— 2012
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
НАЦИОНАЛЬНЫЙ
СТАНДАРТ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
Статистические методы
СПОСОБНОСТЬ ОБНАРУЖЕНИЯЧасть 5
Методология в случаях линейной и нелинейной
калибровки
ISO 11843-5:2008
Capability of detection — Part 5: Methodology in the linear and non-linear
calibration cases
(IDT)
Издание официальное
|
Москва Стандартинформ 2014 |
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией «Научно-исследовательский центр контроля и диагностики технических систем» (АНО «НИЦ КД») на основе собственного аутентичного перевода на русский язык международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 ноября 2012 г. № 1420-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 11843-5:2008 «Способность обнаружения. Часть 5. Методология в случаях линейной и нелинейной калибровки» (ISO 11843-5:2008 «Capability of detection — Part 5: Methodology in the linear and non-linear calibration cases»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в ГОСТ Р 1.0-2012 (раздел 8). Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (gost.ru)
© Стандартинформ, 2014
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
rG — коэффициент вариации отобранного пипеткой меченого антигена (0,9 %); гв — коэффициент вариации отобранного пипеткой объема антисыворотки (1,9 %); rs — (2/3) • (коэффициент вариации отобранного пипеткой объема субстратов хромогена), где коэффициент 2/3 использован для преобразования ошибки отобранного пипеткой объема в ошибку, соответствующую количеству хромогенного продукта, появляющегося на поверхности ячейки в микропланшете (0,6 %); aw — стандартное отклонение результатов измерений поглощательной способности среди ячеек микропланшета и является постоянной в пределах планшета (0,002 поглощательной способности).
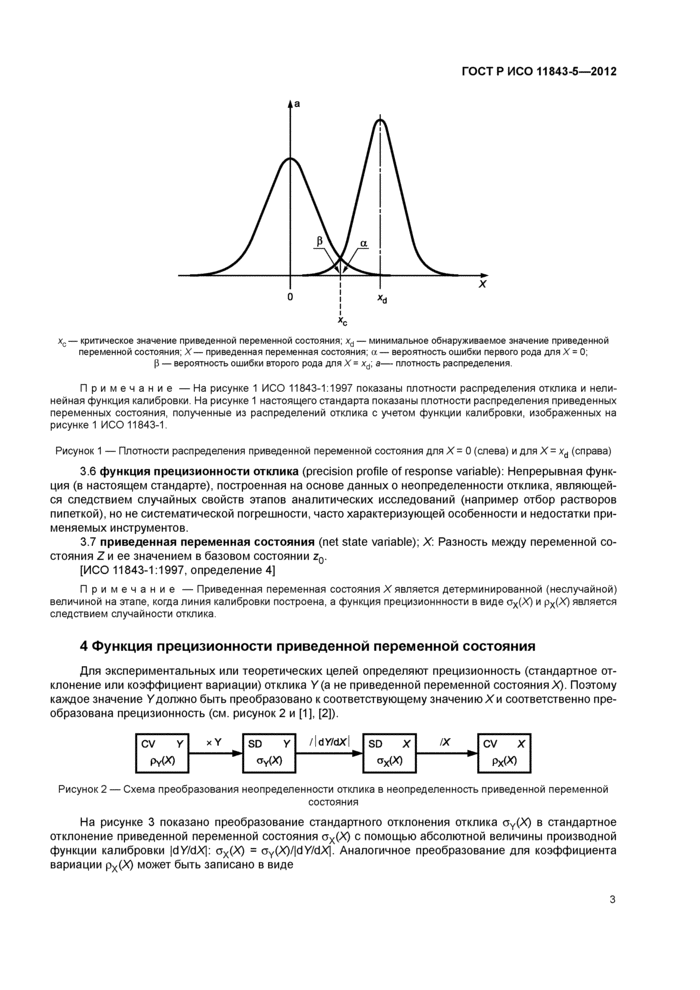
Таким образом, функция прецизионности рх(Х) может быть вычислена по уравнению (11) в соответствии со схемой, представленной на рисунке 2.
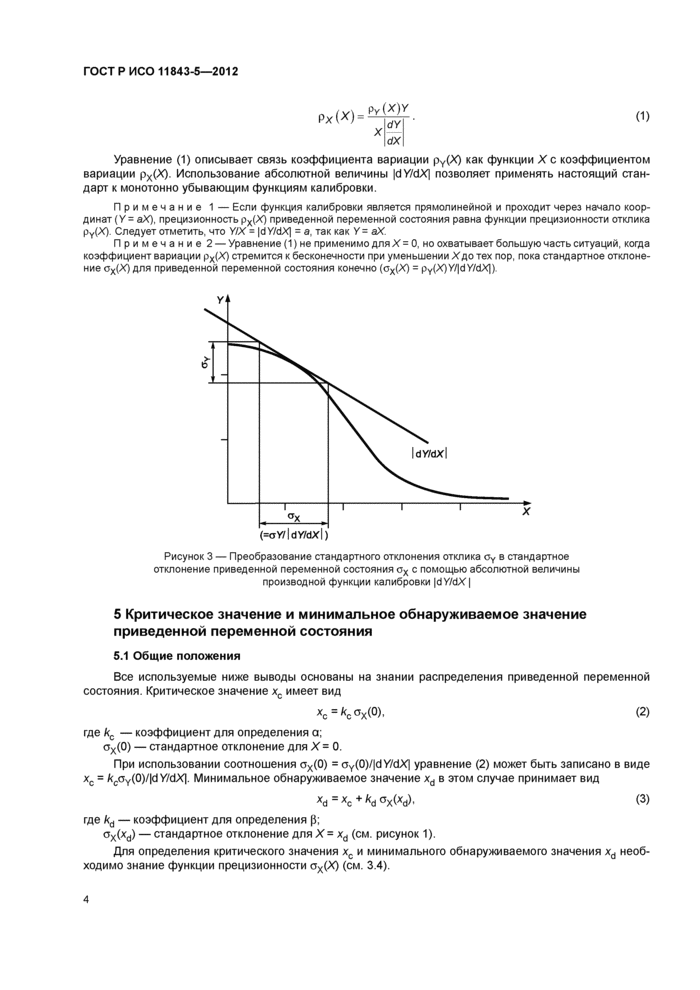
Функция прецизионности рх(Х) для данного примера приведена на рисунке 5. Коэффициент вариации рх(Х) вычислен по уравнению (11) с фактическими параметрами, описанными выше, и выражен в процентах. В случае 5.3 минимальное обнаруживаемое значение xd может быть определено на графике функции прецизионности (см. рисунок 5, стрелка xd). Значение 30 %-ного коэффициента вариации описано в 5.4, примечание 1.
Функции прецизионности в нормальном и полулогарифмическом масштабе дают одно и то же минимальное обнаруживаемое значение. На рисунке 5Ь) не показана точка для Х= 0 и соответствую- 1
|
Ь) Полулогарифмический масштаб Рисунок 5 — Коэффициент вариации приведенной переменной состояния рх(Х) (функция прецизионности) и минимальное обнаруживаемое значение xd в нормальном и полулогарифмическом масштабе для конкурентного имму- ноферментного анализа ELISA |
щее значение коэффициента вариации. Однако данная ситуация не направлена на решение теоретических или практических проблем, а сводится лишь к определению коэффициента вариации в виде функции прецизионности в окрестности минимального обнаруживаемого значения.
6.3 Выбор модели
В иммунологических исследованиях дисперсия отклика может быть аппроксимирована степенной функцией (см. [2])
ау(Х)2ооУ?’, (12)
гдеоу(Х) — стандартное отклонение отклика У. Если) = 0, то дисперсия постоянна. Если) = 1, дисперсия пропорциональна отклику. Если j = 2, коэффициент вариации pY(X) отклика постоянен, коэффициент пропорциональности может быть определен методом наименьших квадратов.
6.4 Применение конкурентного иммуноферментного анализа ELISA
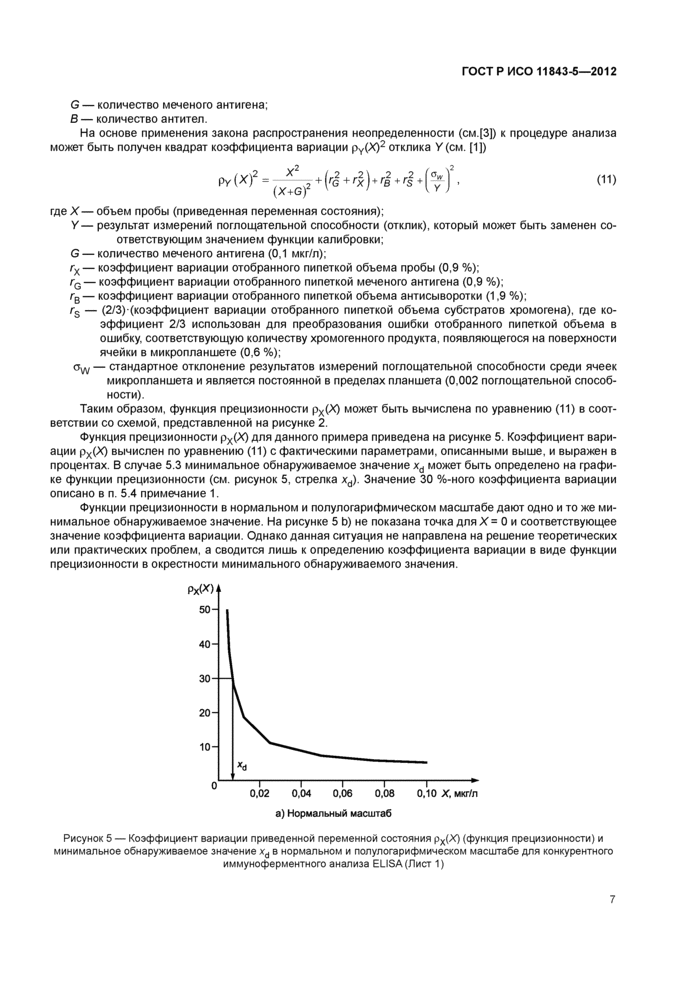
В конкурентном иммуноферментном анализе ELISA часто используют стандартизованную кривую калибровки, называемую 6/В0, и уравнение (10), которое может быть записано в виде (см. [4])
(13)
= Py(*d)
0,132 ’
X=xd
где pY(xd) — коэффициент вариации отклика для X = xd. Обоснование приведено в приложении С.
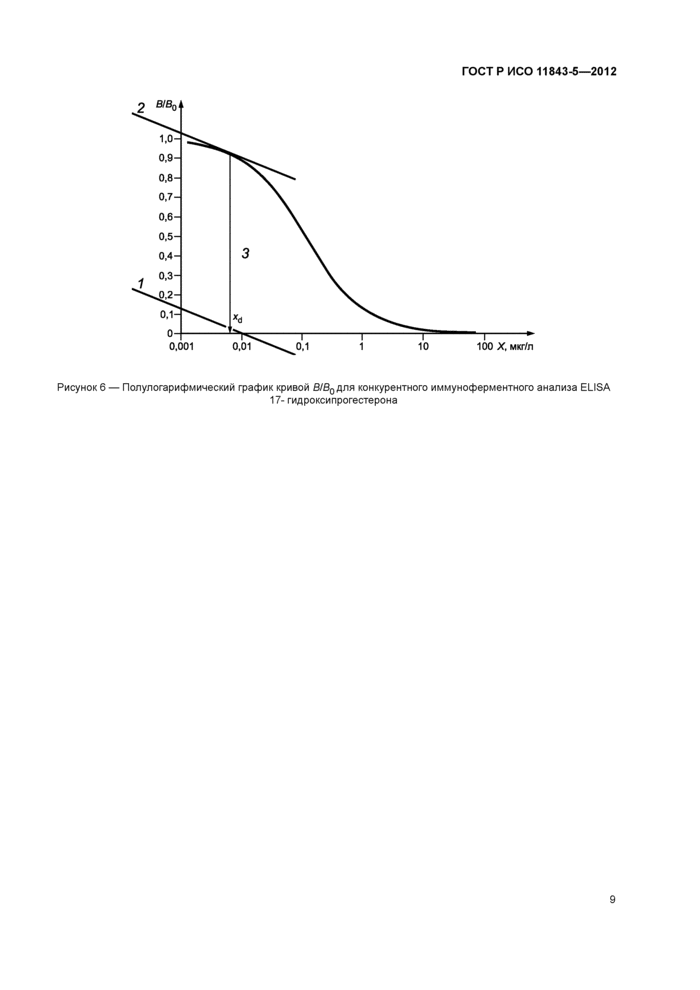
Минимальное обнаруживаемое значение приведенной переменной состояния может быть найдено с использованием уравнения (13). На рисунке 6 приведена полулогарифмическая кривая В/В0 для анализа конкурентным ELISA 17-гидроксипрогестерона (тоже, что в примере 6.2). Если коэффициент вариации отклика должен составлять 1,9 %, коэффициент вариации для пробы с низкой концентрацией используют в качестве приближения Уравнение (13) в этом случае дает результат
0,15 (= 0,019/0,132).
Графическая оценка xd (см. рисунок 6):
- Этап 1. Проводят прямую линию с угловым коэффициентом, вычисленным по уравнению (13) в левосторонней системе координат;
- Этап 2. Проводят касательную к кривой В/В0 параллельно прямой, построенной на этапе 1;
- Этап 3. Опускают перпендикуляр из точки касания на ось X.
Рисунок 6 — Полулогарифмический график кривой 6/Б0 для конкурентного иммуноферментного анализа ELISA 17-гидроксипрогестерона
Точка пересечения перпендикуляра с осью X соответствует xd. Метод обеспечивает почти такой же результат, как в примере 6.2 (рисунки 5 и 6).
ГОСТ Р ИСО 11843-5-2012
Приложение А (обязательное)
Условные обозначения и сокращения, используемые в настоящем стандарте
SD —стандартное отклонение;
CV — коэффициент вариации (SD, деленное на среднее);
POP —стойкий органический загрязнитель;
ELISA —иммуноферментный анализ;
X — приведенная переменная состояния;
У —отклик;
хс — критическое значение приведенной переменной состояния;
xd — минимальное обнаруживаемое значение приведенной переменной состояния;
кс — коэффициент для определения а;
kd — коэффициент для определения Р;
а — вероятность ошибки первого рода для X = 0;
Р — вероятность ошибки второго рода для X = xd;
оу(Х) — стандартное отклонение отклика как функция X
Ру(Х) — коэффициент вариации отклика как функция X;
ах(Х) — стандартное отклонение приведенной переменной состояния как функция X рх(Х) — коэффициент вариации приведенной переменной состояния как функция X;
|dV7dX| — производная функции калибровки;
В/В0 — отношение результатов измерений для произвольной концентрации к результатам измерений для нулевой концентрации. 2
Приложение В (справочное)
Обоснование уравнения (9)
dY
dX
aY(xd)
CTy(xd)
aY(xd)xd
dY
V'c • 6/
dY
1 v,vc 1 "dV
dY
dX
dlnX
X = XJ Xd
dlnX
dY
dX
|
aY(xd) CTy(xd) aY(xd)xd | ||||||||||||
|
Для преобразования уравнения (7) может быть использовано уравнения (1) с учетом перехода к IgX
*d = (кс + kd)
dY
dlnX
где абсолютное значение производной используют в случае, когда угловой коэффициент отрицателен. Деление на неизвестную переменную xd обеих частей этого уравнения дает уравнение
(кс + kd) °v(xd)-
Преобразование натурального логарифма в десятичный логарифм (1пХ = 2,303 • IgX) приводит к искомому уравнению (9) (см. [4]).
10
Приложение С (справочное)
Обоснование уравнения (13)
В конкурентном иммуноферментном анализе ELISA кривая калибровки представляет собой логистическую функцию четырех параметров
|
У = |
+ С3 |
и в стандартизованной форме имеет вид В/В0
|
В 1 |
где С0, С.|, С2 и С3 — коэффициенты, определяемые методом наименьших квадратов, соответствующие реальным данным при калибровке. Подставляя dY = (С0 - С3) dB/B0 в уравнение (10) получаем
dS/50 _ау(Х)/(С0 -С3) dlnX 0,132
Так как коэффициент С0 соответствует наибольшему отклику для пустой пробы (X = 0), а С3 — наименьшему отклику при бесконечной концентрации (X = со), оу(Х)/(С0 - С3) приблизительно равно оу(Х)/С0. Если ру(Х) имеет вид
Ру(*) =
qy(X)
С0 -С3
оу(Х)
Со
где оу{Х)1С0 — коэффициент отклика для пустой пробы ру(0), то последние два уравнения приводят к уравнению (13) (см. также [4]).
11
Приложение ДА (справочное)
Сведения о соответствии ссылочных международных стандартов ссылочным национальным стандартам Российской Федерации
|
Таблица ДА.1 | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
12
ГОСТ Р ИСО 11843-5-2012Библиография
[1] HAYASHI, Y., MATSUDA, R„ MAITANI, Т., IMAI, К., NISHIMURA, W., ITO, К. and MAEDA, М. Precision, limit of detection and range of quantitation in competitive ELISA. Anal. Chem., 76(5), 2004, pp. 1 295—1 301
[2] DUDLEY, R.A., EDWARDS, P., EKINS, R.P., FINNEY, D.J., MCKENZIE, RAAB, G.M., RODBARD, D. and
RODGERS, R.P.C. Guidelines for immunoassay data processing. Clin. Chem., 31(8), 1985, pp. 1 264—1 271
[3] Guide to the expression of uncertainty in measurement (GUM), BIPM, I EC, IFCC, ISO, IUPAC, IUPAP, 01 ML, 1993)3)
[4] HAYASHI, Y., MATSUDA, R„ ITO, K„ NISHIMURA, W„ IMAI, K. and MAEDA, M. Detection limit estimated from slope of calibration curve: An application to competitive Elisa. Anal. Sci., 21, 2005, pp. 167—169
[5] ISO 3534-3:1999, Statistics —Vocabulary and symbols — Part 3: Design of experiments (ИСО 3534-3:1999 Статистика. Словарь и условные обозначения. Часть 3. Планирование эксперимента)4)
УДК 658.562.012.7:65.012.122:006.354 ОКС 03.120.30; Т59
17.020
Ключевые слова: измерение, отклик, стандартное состояние, базовое состояние, приведенная переменная состояния, калибровка, критическое значение отклика, ошибка первого рода
14
Редактор С.Д. Золотова Технический редактор В.Н. Прусакова Корректор И.А. Королева Компьютерная верстка О.Д. Черепковой
Сдано в набор 25.02.2014. Подписано в печать 18.03.2014. Формат 60 х 84^. Гарнитура Ариал. Уел. печ. л. 2,32. Уч.-изд. л. 1,80. Тираж 113 экз. Зак. 442.
Издано и отпечатано во ФГУП «СТАНДАРТИНФОРМ», 123995 Москва, Гранатный пер., 4. www.gostinfo.ru info@gostinfo.ru
Содержание
1 Область применения............................................1
2 Нормативные ссылки............................................1
3 Термины и определения..........................................2
4 Функция прецизионности приведенной переменной состояния.....................3
5 Критическое значение и минимальное обнаруживаемое значение приведенной переменной
состояния..................................................4
6 Примеры...................................................5
Приложение А (обязательное) Условные обозначения и сокращения, используемые в настоящем
стандарте .......................................... 9
Приложение В (справочное) Обоснование уравнения (9).......................10
Приложение С (справочное) Обоснование уравнения (13).......................11
Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов
ссылочным национальным стандартам Российской Федерации...........12
Библиография................................................13
Введение
На практике часто используют как линейные, так и нелинейные функции калибровки. В настоящем стандарте рассмотрены оба случая применительно к оценке способности обнаружения на основе исследования распределений вероятностей приведенной переменной состояния (измеряемой величины), а не только функции калибровки.
В настоящем стандарте использованы основные понятия ИС011843-21), включая вероятностные требования к а и |3и случай линейной калибровки. В интервале значений от соответствующих базовому состоянию до минимального обнаруживаемого значения может быть применена линейная функция калибровки. Таким образом, обеспечена совместимость настоящего стандарта с ИСО 11843-2.
При сравнении аналитического метода, использующего линейную функцию калибровки, с аналогичным методом, использующим нелинейную функцию калибровки, рекомендуется применять настоящий стандарт. В случае линейной калибровки применимы ИСО 11843-2 и настоящий стандарт. Методы ИСО 11843-2, рассматривающие прецизионность для одной переменной отклика, дают тот же результат, что и применение настоящего стандарта, который требует исследования прецизионности для переменной отклика и для переменной состояния, так как исследование прецизионности отклика — то же, что и исследование прецизионности приведенной переменной состояния в случае линейной калибровки.
Применяемый в настоящем стандарте международный стандарт разработан техническим комитетом ИСО/ТС 69 «Применение статистических методов».
^ ИСО 11843-2:2000 «Способность обнаружения. Часть 2. Методология в случае линейной калибровки» (ISO 11843-2:2000 «Capability of detection — Part 2: Methodology in the linear calibration case»).
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы СПОСОБНОСТЬ ОБНАРУЖЕНИЯ Часть 5
Методология в случаях линейной и нелинейной калибровки
Statistical methods. Capability of detection. Part 5. Methodology in the linear and non-linear calibration cases
Дата введения — 2013—12—01
1 Область применения
В настоящем стандарте рассмотрены линейные и нелинейные функции калибровки и установлены основные методы:
- построения функции прецизионности отклика, а именно, описания стандартного отклонения (SD1)) или коэффициента вариации (CV2)) отклика как функции приведенной переменной состояния;
- преобразования функции прецизионности в аналогичную функцию для приведенной переменной состояния и функции калибровки;
- использования полученной функции для оценки критического значения и минимального обнаруживаемого значения приведенной переменной состояния.
Методы, приведенные в настоящем стандарте, применимы, например, для проверки обнаружения какого-либо вещества различным измерительным оборудованием, к которым не может быть применен ИСО 11843-2. Эти методы могут быть применимы к стойким органическим загрязнителям (POP3)) окружающей среды, таким как диоксины, пестициды и гормоноподобные химические вещества при помощи конкурентного ELISA4) (иммуноферментный анализ) и тестов на наличие бактериальных эндотоксинов, вызывающих у человека гипертермию.
Определение и применение критического значения и минимального обнаруживаемого значения приведенной переменной состояния установлены в ИСО 11843-1 и ИСО 11843-2. В настоящем стандарте расширены методы, приведенные в ИСО 11843-2, на случай нелинейной калибровки.
Критическое значение хс и минимальное обнаруживаемое значение xd даны в единицах приведенной переменной состояния. Если хс и xd определены на основе распределения отклика, определение должно включать функцию калибровки, связывающую отклик с приведенной переменной состояния. Настоящий стандарт позволяет определить хс и xd на основе распределения приведенной переменной состояния независимо от вида функции калибровки, а следовательно, независимо от ее линейности или нелинейности.
Функция калибровки должна быть непрерывной, дифференцируемой и монотонно возрастающей или убывающей.
В стандарте рассмотрены случаи, когда стандартное отклонение или коэффициент вариации известны только в окрестности минимального обнаруживаемого значения.
В пунктах 6.2, 6.3, и 6.4 настоящего стандарта приведены соответствующие примеры.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 3534-1 Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах (ISO 3534-1, Statistics — Vocabulary and symbols — Part 1: General statistical terms and terms used in probability)
1) SD — standard deviation.
2> CV — coefficient of variation.
3) pop — persistent organic pollutants.
4) ELISA — enzyme-linked immunosorbent assay.
Издание официальное
ИСО 3534-2 Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика (ISO 3534-2, Statistics — Vocabulary and symbols — Part 2: Applied statistics)
ИСО 3534-3 Статистика. Словарь и условные обозначения. Часть 3. Планирование эксперимента (ISO 3534-3, Statistics — Vocabulary and symbols — Part 3: Design of experiments)
ИСО 5725-1 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Общие принципы и определения (ISO 5725-1, Accuracy (trueness and precision) of measurement methods and results — Part 1: General principles and definitions)
ИСО 11843-1:1997 Способность обнаружения. Часть 1. Термины и определения (ISO 11843-1:1997, Capability of detection — Part 1: Terms and definitions)
ИСО 11843-2:2000 Способность обнаружения. Часть 2. Методология в случае линейной калибровки (ISO 11843-2:2000, Capability of detection — Part 2: Methodology in the linear calibration case)
3 Термины и определения
В настоящем стандарте применены термины по ИСО 3534 (все части), ИСО 5725-1, ИСО 11843-1, а также следующие термины с соответствующими определениями:
3.1 критическое значение приведенной переменной состояния; хс (critical value of the net
state variable): Значение приведенной переменной состояния X, превышение которого для заданной вероятности ошибки а приводит к решению о том, что наблюдаемая система не находится в базовом состоянии (см. рисунок 1).
[ИСО 11843-1:1997, 3.10]
3.2 минимальное обнаруживаемое значение приведенной переменной состояния
(minimum detectable value of the net state variable); xd: Значение приведенной переменной состояния X в действительном состоянии, которое с вероятностью (1 -р) ведет к заключению, что система не находится в базовом состоянии.
|
Примечание — Адаптированное определение по ИСО 11843-1:1997 и ИСО 11843-1:1997/Сог. 1:2003 (см. рисунок 1). |
|
хс — критическое значение приведенной переменной состояния; xd — минимальное обнаруживаемое значение приведенной переменной состояния; X— приведенная переменная состояния; а — вероятность ошибки первого рода для X = 0; р — вероятность ошибки второго рода для X = xd; а — плотность распределения |
Примечание — На рисунке 1 ИСО 11843-1:1997 показаны плотности распределения отклика и нелинейная функция калибровки. На рисунке 1 настоящего стандарта показаны плотности распределения приведенных переменных состояния, полученные из распределений отклика с учетом функции калибровки, изображенных на рисунке 1 ИСО 11843-1.
Рисунок 1 — Плотности распределения приведенной переменной состояния для Х= 0 (слева) и для Х= xd
(справа)
3.3 прецизионность (способности обнаружения) (precision): Стандартное отклонение наблюдаемого отклика или стандартное отклонение приведенной переменной состояния при оценке с применением функции калибровки.
Примечание 1 — При необходимости в качестве оценки прецизионности вместо стандартного отклонения может быть использован коэффициент вариации.
Примечание 2 — В настоящем стандарте прецизионность определена в условиях повторяемости (ИСО 3534-2).
Примечание 3 — В настоящем стандарте использованы термины «прецизионность» и «функция прецизионности» вместо терминов «погрешность» и «функция погрешности».
3.4 функция прецизионности (способности обнаружения) (precision profile): Математическое описание стандартного отклонения или коэффициента вариации отклика или приведенной переменной состояния как функции приведенной переменной состояния.
3.5 отклик (response variable); У: Переменная, представляющая результат эксперимента.
[ИСО 3534-3:1999, 1.2]
Примечание 1 — В стандартах серии ИСО 11843 под откликом следует понимать непосредственно наблюдаемую переменную взамен переменной состояния Z.
Примечание 2 — Отклик У является случайной величиной, представляющей собой результат преобразования с помощью функции калибровки приведенной переменной состояния. Прецизионность отклика описывают с помощью стандартного отклонения ах(Х) и коэффициента вариации рх(Х) приведенной переменной состояния соответственно.
3.6 функция прецизионности отклика (precision profile of response variable): Непрерывная функция (в настоящем стандарте), построенная на основе данных о неопределенности отклика, являющейся следствием случайных свойств этапов аналитических исследований (например, отбор растворов пипеткой), но не систематической погрешности, часто характеризующей особенности и недостатки применяемых инструментов.
3.7 приведенная переменная состояния (net state variable); X: Разность между переменной состояния Z и ее значением в базовом состоянии z0.
[ИСО 11843-1:1997, определение 4]
Примечание — Приведенная переменная состояния X является детерминированной (неслучайной) величиной на этапе, когда линия калибровки построена, а функция прецизионнности в виде <тх(Х) и рх(Х) является следствием случайности отклика.
4 Функция прецизионности приведенной переменной состояния
Для экспериментальных или теоретических целей определяют прецизионность (стандартное отклонение или коэффициент вариации) отклика У (а не приведенной переменной состояния X). Поэтому каждое значение У должно быть преобразовано к соответствующему значению X и соответственно преобразована прецизионность (см. рисунок 2 и [1], [2]).
| ||||||||||||||
|
Рисунок 2 — Схема преобразования неопределенности отклика в неопределенность приведенной переменной состояния |
На рисунке 3 показано преобразование стандартного отклонения отклика сту(Х) в стандартное отклонение приведенной переменной состояния ох(Х) с помощью абсолютной величины производной функции калибровки |с1У/с1Х|: ох(Х) = оу(Х)/|с1У/с1Х|. Аналогичное преобразование для коэффициента вариации рх(Х) может быть записано в виде
Рх(*) =
Ру(Х)У
х
6У
dX
(1)
Уравнение (1) описывает связь коэффициента вариации ру(Х) как функции X с коэффициентом вариации рх(Х). Использование абсолютной величины |d V7dX| позволяет применять настоящий стандарт к монотонно убывающим функциям калибровки.
3
Примечание 1 — Если функция калибровки является прямолинейной и проходит через начало координат (У = аХ), прецизионность рх(Х) приведенной переменной состояния равна функции прецизионности отклика Py(X). Следует отметить, что YIX = |dV7dX| = а, так как У = аХ.
|
Рисунок 3 — Преобразование стандартного отклонения отклика оу в стандартное отклонение приведенной переменной состояния ах с помощью абсолютной величины производной функции калибровки |dy/dX| |
Примечание 2 — Уравнение (1) не применимо для Х= 0, но охватывает большую часть ситуаций, когда коэффициент вариации Рх(Х) стремится к бесконечности при уменьшении Хдо тех пор, пока стандартное отклонение ох(Х) для приведенной переменной состояния конечно (с^(Х) = ру(Х)У/|бУ/бХ|).
5 Критическое значение и минимальное обнаруживаемое значение приведенной переменной состояния5.1 Общие положения
Все используемые ниже выводы основаны на знании распределения приведенной переменной состояния. Критическое значение хс имеет вид
хс = ксах(0), (2)
где кс — коэффициент для определения а; ах(0) — стандартное отклонение для Х= 0.
При использовании соотношения ох(0) = oy(0)/|dy/dX| уравнение (2) может быть записано в виде хс = кс oY(0)/|dy/dX|. Минимальное обнаруживаемое значение xd в этом случае принимает вид
*d = хс + кй °x(*d)> (3)
где kd — коэффициент для определения Р; ox(xd) — стандартное отклонение для Х= xd (см. рисунок 1).
Для определения критического значения хс и минимального обнаруживаемого значения xd необходимо знание функции прецизионности с^(Х) (см. 3.4).
Примечание 1 — Если приведенная переменная состояния подчиняется нормальному распределению, коэффициенты кс = кй = 1,65 соответствуют а = р = 0,05 (5 %).
Примечание 2 — В случае предположения о том, что сгх(Х) является константой (ах(Х) = ах) и кс = kd = 1,65, уравнения (2) и (3) могут быть записаны в виде xG = 1,65 сгх и xd = З.ЗОсу.
5.2 Вычисление вероятности а
(4)
(4)
Если стандартное отклонение определяют для X = 0, то вместо ox(xd) используют ох(0), тогда хс и xd принимают вид
*с = *с°х(0).
4
*d = (*с + *d)ox(0)- (5)
В этом случае уравнение (4) совпадает с уравнением (2) и вероятность а вычисляют в соответствии с ее общим определением. Однако вероятность р может отличаться от исходной. Для этих вычислений знание всей функции прецизионности ах(Х) не требуется.
Примечание — В случае предположения о том, что <тх(Х) является константой (ах(Х) = ох) и kc = kd = 1,65, уравнения (4) и (5) могут быть записаны в виде хс = 1,65сгх и xd = 3,30с^.
5.3 Вычисление вероятности р
При использовании ox(xd) вместо стх(0) в 5.2 выражения для хс и xd принимают вид
хс = *сОх(*d). (6)
xd = (кс + *d)°x(*d)- (7)
В этом случае вероятность рвычисляют в соответствии с ее общим определением. Вероятность а может отличаться от исходной.
Примечание — В случае предположения о том, что сгх(Х) является константой (стх(Х) = стх) и кс = kd = 1,65, уравнения (6) и (7) могут быть записаны в виде хс = 1,65сгх и xd = 3,30с^.
5.4 Дифференциальный метод
(8)
Подход 5.3 имеет практическое преимущество при использовании уравнения (10). Уравнение (7) может быть записано в виде
Px(*d) = ax(*dV*d = М*с + *d)-
Это уравнение дает коэффициент вариации приведенной переменной состояния для X = xd. Преимущество уравнения (8) состоит в том, что минимальное обнаруживаемое значение xd может быть определено как значение приведенной переменной состояния, у которой коэффициент вариации для среднего приведенной переменной состояния равен V(kc + /cd) • 100 %. Для вычисления хс и xd необходимо, чтобы функция прецизионности ах(Х) была непрерывной.
dY
dlgX
(9)
- 2,303(кс + /fd)oy(xd)
X=xd
Для полулогарифмического графика (Уот IgX) угловой коэффициент функции калибровки d Y/dlgX зависит от приведенной переменной состояния Xи принимает установленное значение для минимального обнаруживаемого значения
где левая часть уравнения представляет собой абсолютную величину производной |d Y/dlgX| дляХ = xd (In 10 = 2,303). Это уравнение является общим для кривых калибровки независимо от вида функции калибровки (линейной или нелинейной). Обоснование уравнения (9) приведено в приложении В.
Примечание 1 — Если кс = kd = 1,65, уравнение (8) может быть записано в виде ах(Х) = 1/3,30 = 30 %, а xd расположено в точке X, для которой коэффициент вариации составляет 30 %.
Примечание 2 — Если кс = kd = 1,65, уравнение (9) может быть записано в виде
dY _ aY(xd) (10)
d lg X у 0,132’
A - Xd
где 0,132 = 1/(3,3-2,303).
6 Примеры
6.1 Общие положения
В подпунктах 6.2 и 6.3 рассмотрены примеры оценки функции прецизионности (см. 3.4) в виде стандартного отклонения или коэффициента вариации отклика. Итоговое значение рх(Х) получено на основе непрерывного графика стандартного отклонения или коэффициента вариации отклика в соответствии с разделом 4.
В примере пункта 6.4 показано применение дифференциального метода в случае конкурентного иммуноферментного анализа ELISA. Пример показывает, что функция калибровки для конкурентного иммуноферментного анализа ELISA обычно нелинейна, но предположение о линейности может быть использовано в окрестностях минимального обнаруживаемого значения. 5
6.2 Закон распространения неопределенности
Конкурентный иммуноферментный анализ ELISA для 17-гидроксипрогестерона использован в качестве примера. Экспериментальная процедура ELISA представлена на рисунке 4. Анализ выполнен на микропланшете с 96-ю ячейками. Линия калибровки построена для микропланшета, а фактический анализ образцов выполнен на других ячейках того же самого микропланшета. Здесь проверяется неопределенность в пределах планшета.
|
Рисунок 4 — Экспериментальная процедура ELISA |
Неопределенность конкурентного иммуноферментного анализа ELISA получена на основе конкурентной реакции между веществом проб и меченым антигеном. Отклик У (здесь результатом измерений является поглощательная способность) пропорционален концентрации меченого антигена и антител (антисыворотка) на поверхности ячейки в микропланшете (см. [1]).
где X— объем пробы (приведенная переменная состояния);
G — количество меченого антигена;
В — количество антител.
На основе применения закона распространения неопределенности (см.[3]) к процедуре анализа может быть получен квадрат коэффициента вариации pY(X)2 отклика У (см. [1]).
pY(X)2 =
X"
(X + GY
+ (rn +rX2) + rF
+ г; +
(11)
где X— объем пробы (приведенная переменная состояния);
У— результат измерений поглощательной способности (отклик), который может быть заменен соответствующим значением функции калибровки;
G — количество меченого антигена (0,1 мкг/л);
гх — коэффициент вариации отобранного пипеткой объема пробы (0,9 %);
6
1
2
3
) Стандарт заменен на ISO/IEC Guide 98-3:2008, Uncertainty of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM:1995), которому соответствует национальный стандарт ГОСТ Р 54500.3-2011/ Руководство ИСО/МЭК 98-3:2008 Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения.
4
) Официальный перевод этого стандарта находится в Федеральном информационном фонде технических регламентов и стандартов.
13
5