ГОСТ Р ИСО 11843-2-2007
Статистические методы. Способность обнаружения. Часть 2. Методология в случае линейной калибровки
Устанавливает следующие основные методы:
- планирования эксперимента для оценки критического значения приведенной переменной состояния, критического значения отклика и минимального обнаруживаемого значения приведенной переменной состояния;
- оценки указанных характеристик по экспериментальным данным в случае, когда функция калибровки является линейной, а стандартное отклонение является или константой, или линейно связано с приведенной переменной состояния.
Оглавление
1 Область применения
2 Нормативные ссылки
3 Термины и определения
4 Планирование экспериментов
5 Критические значения Ус и Хс и минимальное обнаруживаемое значение Хd серии измерений
6 Минимальное обнаруживаемое значение для метода измерений
7 Использование полученных результатов
Приложение А Условные обозначения и сокращения
Приложение В Обоснование приведенных формул
Приложение С Примеры
Приложение D Сведения о соответствии национальных стандартов Российской Федерации ссылочным международным стандартам
Библиография
24 страницы
| Дата введения | 01.07.2007 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Строительство
- Раздел Экология
Организации:
| 28.02.2007 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 25-ст |
|---|---|---|---|
| Разработан | ОАО НИЦ КД | ||
| Разработан | ТК 125 Статические методы в управлении качеством продукции | ||
| Издан | Стандартинформ | 2007 г. |
Statistical methods. Capability of detection. Part 2. Methodology in the linear calibration case
ГОСТ Р 50779.10-2000Статистические методы. Вероятность и основы статистики. Термины и определения. Заменен на ГОСТ Р ИСО 3534-1-2019.ГОСТ Р 50779.11-2000Статистические методы. Статистическое управление качеством. Термины и определения. Заменен на ГОСТ Р ИСО 3534-2-2019.- Федеральный закон 184-ФЗ О техническом регулировании
- Р 50.1.040-2002 Статистические методы. Планирование экспериментов. Термины и определения
ГОСТ Р 1.0-2004Стандартизация в Российской Федерации. Основные положения. Заменен на ГОСТ Р 1.0-2012.ГОСТ Р 1.5-2004Стандартизация в Российской Федерации. Стандарты национальные Российской Федерации. Правила построения, изложения, оформления и обозначения. Заменен на ГОСТ Р 1.5-2012.- Показать все
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8
стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18
стр. 19
стр. 20

стр. 21
стр. 22

стр. 23

стр. 24
ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ |
ГОСТ Р ИСО |
СТАТИСТИЧЕСКИЕ МЕТОДЫ
СПОСОБНОСТЬ ОБНАРУЖЕНИЯ
ЧАСТЬ 2
МЕТОДОЛОГИЯ В СЛУЧАЕ ЛИНЕЙНОЙ КАЛИБРОВКИ
ISO 11843-2:2000
Capability of detection -
Part 2: Methodology in the linear calibration case
(IDT)
Москва
Стандартинформ
2007
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО НИЦ КД) и Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции» на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 28 февраля 2007 г. № 25-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 11843-2:2000 «Способность обнаружения. Часть 2. Методология в случае линейной калибровки» (ISO 11843-2:2000 «Capability of detection - Part 2: Methodology in the linear calibration case»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении D
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
СОДЕРЖАНИЕ
|
1 Область применения. 3 2 Нормативные ссылки. 4 3 Термины и определения. 4 4 Планирование экспериментов. 4 5 Критические значения ус, хс и минимальное обнаруживаемое значение xd серии измерений. 5 6 Минимальное обнаруживаемое значение для метода измерений. 10 7 Использование полученных результатов. 11 Приложение А Условные обозначения и сокращения. 11 Приложение В Обоснование приведенных формул. 14 Приложение С Примеры.. 18 Приложение D Сведения о соответствии национальных стандартов Российской Федерации ссылочным международным стандартам.. 21 Библиография. 21 |
Введение
Идеальной способностью обнаружения относительно выбранной переменной состояния является такая, при которой действительное состояние каждой наблюдаемой системы может быть классифицировано как равное или отличное от ее базового состояния. Однако из-за систематических и случайных отклонений это требование не может быть выполнено по следующим причинам:
- в действительности все стандартные состояния, включая базовое состояние, никогда не известны в терминах переменной состояния. Следовательно, все состояния могут быть правильно характеризованы только в терминах отличий от базового состояния, то есть в терминах приведенной переменной состояния;
- на практике стандартные состояния часто используют, чтобы определить состояние через переменную состояния. Другими словами, значение переменной состояния для базового состояния равно нулю. Например, в аналитической химии неизвестную концентрацию или количество анализируемого вещества в материале холостой пробы обычно принимают равным нулю, а значения приведенной концентрации или количества вещества фиксируют в терминах предполагаемых концентраций или количеств. В химическом анализе часто можно оценить только концентрацию или разность количества вещества относительно доступного материала холостой пробы. Чтобы предотвратить ошибочные решения, обычно рекомендуют фиксировать только отличия от базового состояния, то есть значения приведенной переменной состояния.
Примечание - В Руководстве ИСО 30 и в ИСО 11095 никаких различий между переменной состояния и приведенной переменной состояния не делается. Как следствие в этих двух документах стандартное состояние предполагается известным относительно переменной состояния;
- калибровка, процессы отбора и подготовки проб вносят дополнительные случайные отклонения в результаты измерений.
ГОСТ Р ИСО 11843-2-2007
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
СПОСОБНОСТЬ ОБНАРУЖЕНИЯ
Часть 2
Методология в случае линейной калибровки
Statistical methods. Capability of detection.
Part 2. Methodology in the linear calibration case
Дата введения - 2007-07-01
1 Область применения
Настоящий стандарт устанавливает следующие основные методы:
- планирования эксперимента для оценки критического значения приведенной переменной состояния, критического значения отклика и минимального обнаруживаемого значения приведенной переменной состояния;
- оценки указанных характеристик по экспериментальным данным в случае, когда функция калибровки* является линейной, а стандартное отклонение является или константой, или линейно связано с приведенной переменной состояния.
* Аналогом функции калибровки в российских стандартах является градуировочная кривая.
Методы, установленные настоящим стандартом, применимы к различным ситуациям, таким как проверка наличия некоторого вещества в материале, излучение энергии образцами или растениями или изменения геометрии статических систем под воздействием деформации.
Критические значения для оценки неизвестных состояний систем, включенных в серию, могут быть определены на основе реальной серии измерений, учитывая, что минимальное обнаруживаемое значение приведенной переменной состояния как характеристику метода измерений используют для выбора процесса измерений. Минимальное обнаруживаемое значение может быть установлено в качестве характеристики процесса измерений лаборатории или метода измерений, если соответствующие данные являются доступными для каждого уровня, то есть серии измерений, процесса измерений лаборатории или метода измерений. Минимальные обнаруживаемые значения могут быть различны для серии измерений, процесса измерений лаборатории или метода измерений.
Стандарты серии ИСО 11843 применимы к величинам, измеряемым в соответствии с непрерывной шкалой измерений. Они применимы к процессам измерений и типам измерительного оборудования, у которого функциональную связь между математическим ожиданием отклика и значением переменной состояния описывают функцией калибровки. Если отклик или переменная состояния являются векторными величинами, то методы стандартов серии ИСО 11843 применимы отдельно к компонентам векторов или их функциям.
Обозначения, используемые в настоящем стандарте, приведены в приложении А.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 3534-1:1993 Статистика. Словарь и условные обозначения. Часть 1. Вероятность и основные статистические термины
ИСО 3534-2:1993 Статистика. Словарь и условные обозначения. Часть 2. Статистическое управление качеством
ИСО 3534-3:1999 Статистика. Словарь и условные обозначения. Часть 3. Планирование экспериментов
ИСО 11095:1996 Калибровка линейная с использованием образцовых материалов
ИСО 11843-1:1997 Способность обнаружения. Часть 1. Термины и определения
ИСО Руководство 30:1992 Термины и определения, касающиеся эталонных материалов
3 Термины и определения
В стандарте применены термины и определения по ИСО 3534-1, ИСО 3534-2, ИСО 3534-3, ИСО 11095, ИСО 11843-1 и ИСО Руководство 30.
4 Планирование экспериментов
4.1 Общие положения
Процедура определения значений неизвестного действительного состояния включает отбор выборки, подготовку и непосредственно измерения. Поскольку каждый шаг этой процедуры может вносить искажение, необходимо применять одну и ту же процедуру при описании, подготовке и определении значений неизвестного действительного состояния для всех стандартных состояний и базового состояния, используемых при калибровке.
Для определения различий между значениями, характеризующими одно или большее количество неизвестных действительных состояний и базового состояния, необходимо выбрать план эксперимента, подходящий для сравнения. Экспериментальные единицы такого эксперимента определяют на основе измерений действительных состояний и всех стандартных состояний, используемых при калибровке. Идеальный план эксперимента поддерживает постоянными все известные факторы, влияющие на результат, и управляет неизвестными факторами за счет обеспечения рандомизированного порядка подготовки и выполнения измерений.
В действительности достичь этого трудно, поскольку подготовка и определение значений включенных состояний выполняются последовательно во времени. Однако чтобы выявить главные смещения, изменяющиеся во времени, настоятельно рекомендуется исполнять одну половину калибровки до, а другую - после измерений неизвестных состояний. Однако это возможно только, если объем серии измерений известен заранее и имеется достаточно времени для того, чтобы следовать этому подходу. Если невозможно управлять всеми влияющими факторами, то должно быть представлено описание всех недоказанных предположений.
Многие методы измерений требуют химической или физической обработки образцов до проведения непосредственно измерений. Оба шага процедуры измерений вносят дополнительные искажения результатов измерений. Если требуется повторить измерения, то повторение должно включать весь цикл от подготовки до измерений. Однако во многих ситуациях процедура измерений не может быть повторена полностью, в частности, не все шаги подготовки могут быть повторены для каждого измерения (см. примечание 5.2.1).
4.2 Выбор стандартных состояний
Диапазон значений приведенной переменной состояния, заполненный стандартными состояниями, должен включать:
- нулевое значение приведенной переменной состояния (в аналитической химии образец холостой пробы);
- хотя бы одно значение, близкое к предполагаемому минимальному обнаруживаемому значению на основе априорной информации. Если это требование не выполнено, то эксперимент по калибровке должен быть повторен с другими значениями приведенной переменной состояния.
Стандартные состояния должны быть выбраны таким образом, чтобы значения приведенной переменной состояния (в том числе и для логарифмического масштаба) были приблизительно равноудалены в интервале от минимального до максимального значений. Если стандартные состояния представлены стандартными образцами, то их состав должен быть наиболее близким, по возможности, к составу исследуемого материала.
4.3 Выбор количества стандартных состояний I и количества откликов J, K и L
Выбор стандартных состояний, количества подготовок и повторных измерений должен проводиться с учетом следующих требований:
- количество стандартных состояний I, используемых при калибровке, должно быть не менее трех; однако предпочтительно I = 5;
- количество подготовок для каждого стандартного состояния J (включая базовое состояние) должно быть одинаковым; рекомендуется, по крайней мере, две подготовки (J = 2);
- количество подготовок для действительного состояния K должно совпадать с количеством подготовок для каждого стандартного состояния J;
- количество повторных измерений L, выполняемых при подготовке, должно быть одинаковым; рекомендуется не менее двух повторных измерений (L = 2).
Примечание - Формулы для критических значений и минимального обнаруживаемого значения в разделе 5 справедливы только в предположении, что количество повторных измерений при подготовке является одинаковым для всех измерений стандартных и действительных состояний.
Поскольку отклонения и стоимость при подготовке обычно намного больше, чем при измерениях, оптимальный выбор J, K и L может быть получен на основе оптимизации ограничений на отклонения и затраты.
5 Критические значения ус, хс и минимальное обнаруживаемое значение xd серии измерений
5.1 Основные предположения
Вычисления критических значений и минимального обнаруживаемого значения основаны на предположениях в соответствии с ИСО 11095. В настоящем стандарте методы, приведенные в ИСО 11095, использованы с обобщением 5.3.
Основные предположения по ИСО 11095 следующие:
- функция калибровки линейна;
- измерения отклика всех подготовок и стандартных состояний являются независимыми и подчиняются нормальному распределению, стандартное отклонение которого соответствует стандартному отклонению остатка;
- стандартное отклонение остатка является константой, то есть не зависит от значений приведенной переменной состояния (метод 1) или является линейной функцией приведенной переменной состояния (метод 2).
Решение относительно применимости настоящего стандарта и выбора одной из этих двух ситуаций должно быть основано на априорной информации и визуальной экспертизе данных.
5.2 Метод 1. Постоянное стандартное отклонение
5.2.1 Модель
Модель, основанная на предположениях о линейности функции калибровки и постоянном стандартном отклонении, задается уравнением:
Yij = a + bхi + eij, (1)
где хi - приведенная переменная состояния в состоянии i;
eij - случайные составляющие, которые описывают отклонения, связанные с отбором выборок, подготовкой и ошибками измерений.
В соответствии с предположениями случайные величины eij независимы и нормально распределены с нулевым математическим ожиданием и теоретическим стандартным отклонением остатка s: eij ~ N(0; s2). Поэтому значения отклика Yij также являются случайными величинами с математическим ожиданием Е(Yij) = а + bхi и дисперсией V(Yij) = s2, не зависящей от хi.
Примечание - Если для измерений подготовлено J выборок и каждая из них измерена L раз, так что всего выполнено JL измерений для стандартного состояния, то Yij относятся к среднему L измерений, выполненных на подготовленной выборке.
5.2.2 Оценка функции калибровки и стандартного отклонения остатка
В соответствии с ИСО 11095 оценки (см. примечание) для а, b и s2 определяют по формулам:
; (2)
; (3)
. (4)
Примечание - В отличие от истинных параметров, значения которых не известны, оценки параметров обозначены символом ^.
5.2.3 Вычисление критических значений
Критическое значение отклика определяют по формуле
. (5)
Критическое значение приведенной переменной состояния определяют по формуле
, (6)
где t0,95(v) - квантиль t-распределения уровня 95 % с v = (IJ - 2) степенями свободы. Обоснование этих формул приведено в приложении В.
5.2.4 Вычисление минимального обнаруживаемого значения
Минимальное обнаруживаемое значение определяется по формуле
, (7)
где d = d(v; a; b) - значение параметра нецентральности.
Случайная величина T(v; d), описывающаяся нецентральным t-распределением с v = (IJ - 2) степенями свободы и параметром нецентральности d, удовлетворяет уравнению
P[T(v; d) £ t1-a(v)] = b,
где t1-a(v) - квантиль t-распределения уровня (1 - a) c v степенями свободы. Обоснование данной формулы приведено в приложении В.
Для a = b и v > 3 хорошим приближением d является следующее:
d(v; a; b) » 2t1-a(v), (8)
где t1-a(v) - квантиль t-распределения уровня (1 - a) c v = (IJ - 2) степенями свободы.
Если v = 4 и a = b = 0,05, то относительная ошибка этого приближения составляет 5 %.
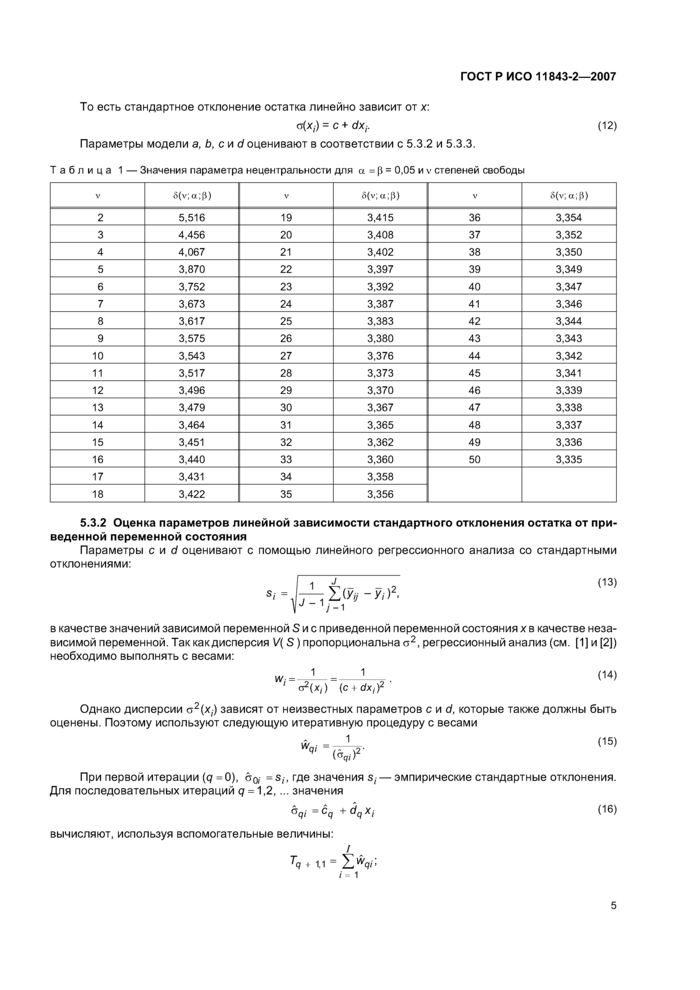
В таблице 1 приведены значения d(v; a; b) для a = b = 0,05 и различных значений v.
Для a = b и v > 3 приближенное значение xd можно определить по формуле
. (9)
5.3 Метод 2. Стандартное отклонение линейно зависит от приведенной переменной состояния
5.3.1 Модель
Модель, основанная на предположениях, что функция калибровки является линейной и стандартное отклонение линейно зависит от приведенной переменной состояния, задается уравнением
Yij = a + bxi + eij, (10)
где xi, а, b и Yij имеют тот же смысл, что и в 5.2.1, а eij - независимые и нормально распределенные случайные величины с математическим ожиданием Е(eij) = 0 и дисперсией:
V(eij) = s2(хi) = (с + dхi)2. (11)
То есть стандартное отклонение остатка линейно зависит от х:
s(хi) = с + dxi. (12)
Параметры модели а, b, с и d оценивают в соответствии с 5.3.2 и 5.3.3.
Таблица 1 - Значения параметра нецентральности для a = b = 0,05 и v степеней свободы
|
v |
d(v; a; b) |
v |
d(v; a; b) |
v |
d(v; a; b) |
|
2 |
5,516 |
19 |
3,415 |
36 |
3,354 |
|
3 |
4,456 |
20 |
3,408 |
37 |
3,352 |
|
4 |
4,067 |
21 |
3,402 |
38 |
3,350 |
|
5 |
3,870 |
22 |
3,397 |
39 |
3,349 |
|
6 |
3,752 |
23 |
3,392 |
40 |
3,347 |
|
7 |
3,673 |
24 |
3,387 |
41 |
3,346 |
|
8 |
3,617 |
25 |
3,383 |
42 |
3,344 |
|
9 |
3,575 |
26 |
3,380 |
43 |
3,343 |
|
10 |
3,543 |
27 |
3,376 |
44 |
3,342 |
|
11 |
3,517 |
28 |
3,373 |
45 |
3,341 |
|
12 |
3,496 |
29 |
3,370 |
46 |
3,339 |
|
13 |
3,479 |
30 |
3,367 |
47 |
3,338 |
|
14 |
3,464 |
31 |
3,365 |
48 |
3,337 |
|
15 |
3,451 |
32 |
3,362 |
49 |
3,336 |
|
16 |
3,440 |
33 |
3,360 |
50 |
3,335 |
|
17 |
3,431 |
34 |
3,358 |
|
|
|
18 |
3,422 |
35 |
3,356 |
5.3.2 Оценка параметров линейной зависимости стандартного отклонения остатка от приведенной переменной состояния
Параметры с и d оценивают с помощью линейного регрессионного анализа со стандартными отклонениями:
, (13)
в качестве значений зависимой переменной S и с приведенной переменной состояния х в качестве независимой переменной. Так как дисперсия V(S) пропорциональна s2, регрессионный анализ (см. [1] и [2]) необходимо выполнять с весами:
. (14)
Однако дисперсии s2(хi) зависят от неизвестных параметров с и d, которые также должны быть оценены. Поэтому используют следующую итеративную процедуру с весами
. (15)
При первой итерации (q = 0), , где значения si - эмпирические стандартные отклонения. Для последовательных итераций q = 1, 2, ... значения
(16)
вычисляют, используя вспомогательные величины:
;
;
; (17)
;
;
; (18)
. (19)
Эти процедуры быстро сходятся для q = 3,
.
Если это последняя итерация, то
, , , т.е.
. (20)
5.3.3 Оценка функции калибровки
Для оценки параметров а и b используют линейный регрессионный анализ с весовыми коэффициентами (см. [1] и [2]). В данном случае - значения зависимой переменной, хi - значения независимой переменной, wi - весовые коэффициенты
.
Здесь - оценка дисперсии хi в соответствии с уравнением (20). Вспомогательные величины в этом случае имеют вид
;
;
;
; (21)
.
Оценки параметров а и b определяют по формулам:
; (22)
. (23)
5.3.4 Вычисление критических значений
Критическое значение отклика определяют по формуле
. (24)
Критическое значение приведенной переменной состояния определяется по формуле
; (25)
где ; (26)
sxxw = T3 - T22/T1; (27)
, (28)
где t0,95(v) - квантиль t-распределения уровня 95 % с v = IJ - 2 степенями свободы.
5.3.5 Вычисление минимального обнаруживаемого значения
Минимальное обнаруживаемое значение определяют по формуле
, (29)
где d = d(v; a; b) - значение параметра нецентральности в соответствии с 5.2.4.
Так как зависит от xd, значение xd следует вычислять итеративным способом.
Итеративная процедура начинается с и xd0. На следующем итеративном шаге вычисляют и используют в формуле для xd, получая xd1, .... Во многих случаях, первый итеративный шаг заметно не изменяет значение xd. Приемлемое значение для xd может быть получено в третьем итеративном шаге.
6 Минимальное обнаруживаемое значение для метода измерений
Минимальное обнаруживаемое значение, полученное при конкретной калибровке, показывает способность калиброванного метода измерений для соответствующей серии измерений обнаруживать значение приведенной переменной состояния, соответствующей наблюдаемому действительному состоянию, отличное от нуля. Таким образом, минимальное обнаруживаемое значение для метода измерений - это наименьшее значение приведенной переменной состояния, которое может быть обнаружено отличным от нуля с вероятностью (1 - b). Минимальные обнаруживаемые значения различаются для различных калибровок. Минимальные обнаруживаемые значения различных серий измерений:
- для конкретного процесса измерений, основанного на том же самом типе процесса измерений;
- для типа процесса измерений, основанного на том же самом методе измерений;
- для метода измерений можно интерпретировать как реализацию случайной величины, для которой параметры распределения можно рассматривать как характеристики процесса измерений, типа процесса измерений или метода измерений, соответственно.
Если для конкретного процесса измерений выполнено m последовательных калибровок для определения минимального обнаруживаемого значения приведенной переменной состояния xd, то можно использовать m минимальных обнаруживаемых значений xd1, xd2, … xdm для определения минимального обнаруживаемого значения для метода измерений при следующих условиях:
a) процесс измерений не изменяется;
b) распределение значений xd унимодально и не имеет удаленных значений xd;
c) планирование эксперимента (включая количество стандартных состояний и количество откликов процедуры J, K и L) одинаково для каждой из калибровок.
При этих условиях медиана значений xdi для i = 1, ..., m рекомендуется в качестве минимального обнаруживаемого значения процесса измерений. Если вместо медианы используют другую суммарную статистику значений xdi, то используемая статистика должна быть описана.
Если любое из этих условий нарушено, то минимальное обнаруживаемое значение процесса измерений определено недостаточно точно и определение общего значения не следует предпринимать. Если один и тот же метод измерений применяют в р лабораториях и для каждой из них определяют минимальное обнаруживаемое значение процесса измерений в пределах лаборатории, то для тех же самых условий, для которых определялось минимальное обнаруживаемое значение процесса измерений, медиана р лабораторных минимальных обнаруживаемых значений рекомендуется в качестве минимального обнаруживаемого значения метода измерений. Если вместо медианы используют другую суммарную статистику лабораторных минимальных обнаруживаемых значений, то используемая статистика должна быть описана.
7 Использование полученных результатов
Примечание - Примеры определения критических и минимальных обнаруживаемых значений приведены в приложении С.
7.1 Критические значения
Для принятия решений относительно достижения действительных состояний следует применять только критические значения приведенной переменной состояния или отклика. Эти значения, полученные при калибровке процесса измерений, являются границами области принятия решений при оценке неизвестных состояний системы, включенных в серию. При последовательных калибровках одного и того же процесса измерений критические значения могут изменяться от одной калибровки к другой. Однако так как каждое из критических значений является границей области принятия решений для соответствующей серии измерений, бессмысленно вычислять общие критические значения для всех калибровок и использовать их в качестве критических значений.
Если значение приведенной переменной состояния или отклика не превышает критического значения, то можно констатировать, что нет различий между наблюдаемым действительным состоянием и базовым состоянием. Однако из-за возможности появления ошибки второго рода это значение не следует рассматривать как демонстрацию того, что наблюдаемая система определенно находится в ее базовом состоянии. Поэтому такое сообщение как «ноль» или «меньшие чем минимальное обнаруживаемое значение» недопустимо. Всегда должно быть указано значение и его неопределенность. Если полученное значение не превышает критического значения, то должен быть добавлен комментарий «не обнаружен».
7.2 Минимальное обнаруживаемое значение
Минимальное обнаруживаемое значение, полученное при конкретной калибровке, показывает, является ли способность обнаружения действительного процесса измерений достаточной для предназначенной цели. Если это не так, то величины J, К или L могут быть изменены.
Минимальное обнаруживаемое значение, полученное по набору калибровок для предположений, упомянутых в разделе 6, может служить для сравнения, выбора или анализа различных лабораторий или методов соответственно.
Приложение А
(обязательное)
Условные обозначения и сокращения
а - свободный член уравнения у = а + bх + e;
- сценка свободного члена а;
b - коэффициент наклона в выражении у = а + bх + e;
- оценка коэффициента наклона b;
с - свободный член уравнения s(х) = с + dx для стандартного отклонения остатка;
- оценка свободного члена с;
d - коэффициент наклона в выражении s(х) = с + dx для стандартного отклонения остатка;
- оценка коэффициента наклона d;
Е() - математическое ожидание случайной величины, указанной в скобках;
I - количество стандартных состояний, используемых в эксперименте при калибровке;
I = 1, ..., I - индекс переменной стандартных состояний;
J - количество подготовок для каждого состояния;
j = 1, ... L - индекс переменной подготовок для стандартных состояний и базового состояния;
К - количество подготовок для действительного состояния;
k = 1, ..., К - индекс переменной подготовок для действительного состояния;
L - количество повторных измерений для каждой подготовки;
l = 1, ..., L - индекс переменной повторных измерений для каждой подготовки;
М - коэффициент;
m - количество последовательных калибровок;
N - количество подготовок в эксперименте при калибровке. Если количество подготовок для каждого стандартного состояния одинаково, то N = IJ, а общее количество измерений в эксперименте при калибровке равно NL;
q = 0, 1, 2, ... - номер шага итерации;
s - эмпирическое стандартное отклонение;
- сумма квадратов отклонений выбранных значений приведенной переменной состояния для стандартных состояний (включая базовое состояние) от выборочного среднего;
- взвешенная сумма квадратов отклонений выбранных значений приведенной переменной состояния для стандартных состояний (включая базовое состояние) от выборочного взвешенного среднего;
Т - вспомогательная величина для линейного регрессионного анализа при использовании весовых коэффициентов;
V() - дисперсия случайной величины, указанной в скобках;
wi - весовой коэффициент хi;
- весовой коэффициент хi в q-м итеративном шаге;
X - приведенная переменная состояния Х = Z - z0;
х - значение приведенной переменной состояния;
x1, ..., xI - выбранные значения приведенной переменной состояния Х для стандартных состояний, включая базовое состояние;
хс - критическое значение приведенной переменной состояния;
xd - минимальное обнаруживаемое значение приведенной переменной состояния;
- выборочное среднее выбранных значений приведенной переменной состояния X для стандартных состояний (включая базовое состояние);
- значение оценки приведенной переменной состояния для конкретного действительного состояния;
- взвешенное среднее выбранных значений приведенной переменной состояния для стандартных состояний (включая базовое состояние);
Y - отклик;
ус - критическое значение отклика;
yijl - l-е измерение j-й подготовки i-го стандартного состояния;
yk1, …, yki - полученные значения отклика для k-й подготовки конкретного действительного состояния в серии измерений;
- выборочное среднее наблюдаемых значений для конкретного действительного состояния;
- выборочное среднее измеренных значений yijl;
- выборочное среднее измеренных значений j-й подготовки i-го стандартного состояния;
- выборочное среднее измеренных значений i-го стандартного состояния;
- среднее KL измеренных значений при х = 0;
Z - переменная состояния;
z0 - значение переменной состояния в базовом состоянии;
a - вероятность ошибочного отклонения нулевой гипотезы «рассматриваемое состояние не отличается от базового состояния относительно переменной состояния» для каждого из наблюдаемых действительных состояний в серии измерений, для которой эта нулевая гипотеза является истинной (вероятность ошибки первого рода).
В случае отсутствия определенных рекомендаций должно быть установлено a = 0,05;
b - вероятность ошибочного принятия нулевой гипотезы «рассматриваемое состояние не отличается от базового состояния относительно переменной состояния» для каждого из наблюдаемых действительных состояний в серии измерений, для которой приведенная переменная состояний равна минимальному обнаруживаемому значению (вероятность ошибки второго рода).
В случае отсутствия определенных рекомендаций должно быть установлено b = 0,05;
d - параметр нецентральности t-распределения;
e - случайная составляющая отклика, характеризующая отклонения при отборе выборки, подготовке и ошибки измерений;
v - число степеней свободы;
sdiff - стандартное отклонение разности между выборочным средним и оценкой ;
- оценка стандартного отклонения остатка;
- стандартное отклонение хi в q-м итеративном шаге;
- оценка стандартного отклонения остатка при х = 0.
Приложение В
(справочное)
Обоснование приведенных формул
В.1 Метод 1. Постоянное стандартное отклонение
Согласно предположениям 5.1 и в случае постоянного стандартного отклонения оценки коэффициентов регрессии и подчиняются нормальному распределению с математическими ожиданиями:
Е() = а; E() = b
и дисперсиями:
; ,
где s2 - дисперсия остатков средних L повторных измерений для каждой подготовки.
Если отклик измерен KL раз в базовом состоянии (z = z0, х = 0), то разность между средним KL значений и оценкой подчиняется нормальному распределению с математическим ожиданием
и дисперсией
Так как подчиняется нормальному распределению, случайная величина
подчиняется стандартному нормальному распределению. Следовательно с вероятностью 0,95 справедливо неравенство
Так как неизвестно, его можно оценить следующим образом:
где - оценка дисперсии остатка в соответствии с регрессионным анализом, которую следует использовать вместо s2. Случайная величина подчиняется t-распределению с v = (IJ - 2) степенями свободы, а приведенное ниже неравенство выполняется с вероятностью 0,95
Таким образом
где - квантиль t-распределения уровня 95 % c v степенями свободы.
Правая сторона этого неравенства является критическим значением отклика
а критическое значение приведенной переменной состояния
В приведенном выражении можно использовать и другие квантили t-распределения при необходимости.
Чтобы определить минимальное обнаруживаемое значение xd приведенной переменной состояния, необходимо исследовать распределение величины в случае, когда истинное значение х приведенной переменной состояния совпадает с минимальным обнаруживаемым значением xd приведенной переменной состояния х = xd. Для обнаружения данного состояния с вероятностью (1 - b) необходимо, чтобы выполнялось условие:
или
Если х = xd, математическое ожидание, имеет вид
Таким образом
а для х = 0.
Так как описывается стандартным нормальным распределением, отношение зависит от U и описывается распределением , случайная величина Т(v; d) описывается нецентральным t-распределением с v степенями свободы и параметром нецентральности d(d = d(v; a; b) для a = 0,05 или другого соответствующего значения. Для Т(v; s) можно записать
Поскольку
для минимального обнаруживаемого значения приведенной переменной состояния справедливо выражение
При определении оценки b и s подставляют в формулу так, что минимальное обнаруживаемое значение принимает вид
Критическое значение отклика ус равно сумме и произведения коэффициента М на , а критическое значение приведенной переменной состояния - произведению коэффициента М на . Если, согласно рекомендациям, значения приведенной переменной состояния стандартных состояний расположены равноудаленно для близкого к нулю значения a = 0,05, а также К = 1 (одна подготовка измерений действительного состояния) или К = J (количество подготовок измерений действительного состояния и стандартных состояний совпадают), то сомножитель
в выражениях для критических значений является функцией только количества стандартных состояний I и количества подготовок каждого стандартного состояния J. Для некоторых случаев значения М приведены в таблице В.1.
Таблица В.1 - Значения коэффициента М
|
Если К = 1 |
|||||
|
I |
J |
IJ |
t0,95(v) |
M |
|
|
3 |
1 |
3 |
1,35 |
6,31 |
8,52 |
|
3 |
2 |
6 |
1,19 |
2,13 |
2,54 |
|
5 |
1 |
5 |
1,26 |
2,35 |
2,97 |
|
5 |
2 |
10 |
1,14 |
1,86 |
2,12 |
|
5 |
4 |
20 |
1,07 |
1,73 |
1,86 |
|
Если К = J |
|||||
|
I |
J |
IJ |
t0,95(v) |
M |
|
|
3 |
1 |
3 |
1,35 |
6,31 |
8,54 |
|
3 |
2 |
6 |
0,96 |
2,13 |
2,04 |
|
5 |
1 |
5 |
1,26 |
2,35 |
2,97 |
|
5 |
2 |
10 |
0,89 |
1,86 |
1,66 |
|
5 |
4 |
20 |
0,63 |
1,73 |
1,09 |
B.2 Метод 2. Стандартное отклонение линейно зависит от приведенной переменной состояния
Согласно предположениям 5.1 и в случае, если стандартное отклонение является линейной функцией приведенной переменной состояния, то оценки коэффициентов линии регрессии и подчиняются нормальному распределению с математическими ожиданиями:
и дисперсиями:
где s2 - такое значение, что (wi/s2) является дисперсией остатков средних при L повторных измерениях и i подготовках.
Если отклик измерен KL раз в базовом состоянии (Z = z0, X= 0), то разность между средним значений и оценкой подчиняется нормальному распределению с математическим ожиданием
и дисперсией
Значение является неизвестным, но его можно оценить по формуле
где - тоже, что и в уравнении (20), а - оценка дисперсии остатка регрессионного анализа, которую следует использовать вместо s2.
По аналогии с В.1 критическое значение отклика и критическое значение приведенной переменной состояния определяют по формулам:
Подобные выражения справедливы и в тех случаях, когда необходимы другие квантили t-распределения.
Эти формулы включают случай постоянного стандартного отклонения, для которого все веса являются равными единице (wi = 1 для i = 1, ..., I) и T1 = IJ, , sxxw = sxx и .
Минимальное обнаруживаемое значение приведенной переменной состояния
,
где для х = xd
При прогнозировании оценки b и (и ),
где
,
подставляют в формулу. Таким образом, минимальное обнаруживаемое значение приведенной переменной состояния определяется по формуле
Так как зависит от значения xd, для оценки следует использовать итеративную процедуру в соответствии с 5.3.5.
Приложение С
(справочное)
Примеры
С.1 Пример 1
Содержание ртути в растительных материалах в нг/г* измеряют методом атомно-абсорбционной спектроскопии. Каждый образец раскладывают, используя микроволновой (MLS-1200) метод в растворе азотной кислоты/бихромата калия. Эти растворы исследованы выделением холодных паров с последующей концентрацией на позолоченной фольге с помощью систем Varian VGA-76 и МСА-90 до проведения атомно-абсорбционных измерений. Для оценки функции калибровки и определения способности обнаружения каждый из шести стандартных образцов, представляющих пустую концентрацию (х = 0) и приведенные концентрации х = 0,2 нг/г; 0,5 нг/г; 1,0 нг/г; 2,0 нг/г; 3,0 нг/г, был подготовлен три раза и каждый подготовленный образец измеряют один раз. Следовательно, I = 6; J = 3; L = 1.
*1 часть на миллиард = 10-9 г/г = 1 нг/г.
Предполагается, что предположения о линейности функции калибровки, постоянном стандартном отклонении и нормальном распределении отклика выполняются; a и b установлены равными a = b = 0,05. Для определения концентрации ртути в исследуемом материале были учтены два различных подхода к выполнению измерений:
a) может быть выполнено одно измерение (К = L = 1);
b) три образца могут быть подготовлены для измерения и каждый из них измерен один раз (К = 3; L = 1), а выборочное среднее наблюдаемых значений используют как результат измерений (результаты эксперимента при калибровке приведены в таблице С.1).
Таблица С.1 - Результаты эксперимента при калибровке для определения содержания ртути в продуктах или медикаментах
|
Стандартный образец i |
Холостая концентрация ртути хi, нг/г |
Поглощаемость уij |
||
|
1 |
0 |
0,003 |
-0,001 |
0,002 |
|
2 |
0,2 |
0,004 |
0,005 |
0,005 |
|
3 |
0,5 |
0,011 |
0,011 |
0,012 |
|
4 |
1,0 |
0,023 |
0,023 |
0,023 |
|
5 |
2,0 |
0,048 |
0,047 |
0,048 |
|
6 |
3,0 |
0,071 |
0,072 |
0,072 |
Данные статистического анализа:
= 1,1167 нг/г;
Sxx = 20,425;
= 9,9959×10-5;
= 0,02374;
= 1,1099×10-3.
Поскольку v = N - 2 = 16;
t0,95(v) = t0,95(16) = 1,746;
d(v, a, b) = d(16; 0,05; 0,05) = 3,440;
(2t0,95(v) = 3,492).
Результаты для подхода, указанного в перечислении а).
Критическое значение отклика [см. формулу (5)] - ус = 0,00305.
Критическое значение приведенной концентрации [см. формулу (6)] - хс = 0,086 нг/г.
Минимальная обнаруживаемая приведенная концентрация [см. формулу (7)] - xd = 0,173 нг/г.
Наименьшее значение поглощаемости, которое может интерпретироваться как испарение ртути из образца с приведенной концентрацией больше, чем из пустой концентрации - ус = 0,00305 критическое значение отклика.
Наименьшая приведенная концентрация ртути в образце, которую метод может отличить (с вероятностью 1 - b = 0,95) от пустой концентрации xd = 0,173 нг/г, минимальное обнаруживаемое значение приведенной концентрации.
Результаты для подхода, указанного в перечислении b).
Критическое значение отклика [см. формулу (5)] - ус = 0,00230.
Критическое значение приведенной концентрации [см. формулу (6)] - хс = 0,055 нг/г.
Минимальная обнаруживаемая приведенная концентрация [см. формулу (7)] - xd = 0,110 нг/г.
С.2 Пример 2
Измеряют количество толуола в вытяжке 100 мкл, используя газовый хроматограф с масс-электрометрическим датчиком (GC/MS). Образцы по 100 мкл были введены в систему GC/MS. Используют шесть стандартных образцов с содержанием толуола в диапазоне от 4,6 пг/100 мкл до 15000 пг/100 мкл. Каждый образец вводили и измеряли четыре раза (I = 6, J = 4, L = 1, N = 24). Результаты измерений приведены в таблице С.2.
Анализ графического представления результатов измерений показывает, что отношение между количеством толуола и откликом (область пика) линейно, стандартное отклонение области пика линейно зависит от количества толуола. Согласно дополнительному предположению о нормальном распределении отклика способность обнаружения определяли согласно 5.3.
Таблица С.2 - Результаты эксперимента при калибровке для определения количества толуола в 100 мкл экстракта
|
Стандартный образец, i |
Приведенное количество толуола xi, пг/100 мкл |
Область пика уij |
Эмпирическое стандартное отклонение, si |
Стандартное отклонение в итерации 1, 2, 3 |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||
|
1 |
4,6 |
29,80 |
16,85 |
16,68 |
19,52 |
6,20 |
4,56 |
5,17 |
5,15 |
|
2 |
23 |
44,60 |
48,13 |
42,27 |
34,78 |
5,65 |
7,07 |
7,93 |
7,92 |
|
3 |
116 |
207,70 |
222,40 |
172,88 |
207,51 |
21,02 |
19,73 |
21,87 |
21,88 |
|
4 |
580 |
894,67 |
821,30 |
773,40 |
936,93 |
73,19 |
82,91 |
91,43 |
91,57 |
|
5 |
3000 |
5350,65 |
4942,63 |
4315,79 |
3879,28 |
652,98 |
412,46 |
454,22 |
455,02 |
|
6 |
15000 |
20718,14 |
24781,61 |
22405,76 |
24863,91 |
2005,02 |
2046,54 |
2253,14 |
2257,23 |
В процедуре оценок для с и d выполняют итеративную процедуру линейного регрессионного анализа в соответствии с 5.3.2, которая дает следующие оценки линейной функции регрессии:
итерация 1: = 3,93323 + 0,136174 хi,
итерация 2: = 4,48284 + 0,149911 хi,
итерация 3: = 4,46228 + 0,150185 хi.
Соответствующие стандартные отклонения приведены в графах 5 - 7 таблицы С.2. После третьей итерации результаты устойчивы, поэтому уравнение итерации 3 может быть использовано как заключительный результат части 1 процедуры оценки, то есть:
= 4,46228 + 0,150185 х;
= 4,46228.
Параметры а и b функции калибровки оценивают в соответствии с 5.3.3 со значениями зависимой переменной уij графы 3 и значениями независимой переменной хi графы 2 с весами
Данные регрессионного анализа:
sxxw = 606,224;
v = N - 2 = 22;
t0,95(v) = t0,95(22) = 1,717.
Поэтому для К = 1 получены следующие результаты.
Критическое значение отклика [см. формулу (24)] - ус = 20,82.
Критическое значение приведенного количества толуола в 100 мкл экстракта [см. формулу (25)] - хс = 5,63 пг.
Минимальное обнаруживаемое значение рассчитывают итеративным методом.
Для a = b = 0,05, d(v; a; b) = d(22; 0,05; 0,05) = 3,397 (см. таблицу 1) и для первое значение для xd [см. уравнение (29)] равно xd0 = 11,139; из этого следует и xd1 = 14,553.
Для итерация второго шага дает xd2 = 15,627 пг/100 мкл.
Для итерация третьего шага дает xd = xd3 = 15,967 пг/100 мкл.
Наименьшая область пика, которая может интерпретироваться как испарение толуола из образца с приведенной концентрацией больше, чем из пустой концентрации, ус = 20,82 - критическое значение отклика.
Наименьшее приведенное количество толуола в образце 100 мкл экстракта, которое может отличить метод (с вероятностью 1 - b = 0,95) от пустой концентрации xd = 15,97 пг/100 мкл - минимальное обнаруживаемое значение приведенной концентрации толуола.
Приложение D
(справочное)
Сведения о соответствии национальных стандартов Российской Федерации ссылочным международным стандартам
|
Обозначение ссылочного международного стандарта |
Обозначение и наименование соответствующего национального стандарта |
|
ИСО 3534-1:1993 |
ГОСТ Р 50779.10-2000 (ИСО 3534-1:1993) Статистические методы. Вероятность и основы статистики. Термины и определения |
|
ИСО 3534-2:1993 |
ГОСТ Р 50779.11-2000 (ИСО 3534-2:1993) Статистические методы. Статистическое управление качеством. Термины и определения |
|
ИСО 3534-3:1999 |
Р 50.1.040-2002 Статистические методы. Планирование экспериментов. Термины и определения |
|
ИСО 11095:1996 |
* |
|
ИСО 11843-1:1997 |
ГОСТ ИСО 11843-1-2007 Статистические методы. Способность обнаружения. Часть 1. Термины и определения |
|
ИСО Руководство 30:1992 |
* |
|
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Перевод данного международного стандарта находится в Федеральном информационном фонде технических регламентов и стандартов. |
|
Библиография
[1] DRAPER N.R. and SMITH H. Applied Regression Analysis. Wiley, New York, 1981
[2] MONTGOMERY D.C. and PECK E.A. Introduction to Linear Regression Analysis. Wiley, New York, 1992
[3] CURRIE L.A. Nomenclature in Evaluation of Analytical Methods Including Detection and Qualification Capabilities. IUPAC Recommendations 1995. Pure and Applied Chemistry, 67, 1995, pp. 1699 - 1723
Ключевые слова: отклик, минимальное обнаруживаемое значение, стандартное состояние, приведенная переменная состояния, критическое значение переменной состояния, линейная калибровка