ГОСТ Р 34.10-2012
Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи
Купить ГОСТ Р 34.10-2012 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
Определяет схему электронной цифровой подписи, процессы формирования и проверки цифровой подписи под заданным сообщением (документом), передаваемым по незащищенным телекоммуникационным каналам общего пользования в системах обработки информации различного назначения. Внедрение цифровой подписи на основе стандарта повышает, по сравнению с ранее действовавшей схемой цифровой подписи, уровень защищенности передаваемых сообщений от подделок и искажений. Стандарт рекомендуется применять при создании, эксплуатации и модернизации систем обработки информации различного назначения.
- Заменяет ГОСТ Р 34.10-2001 «Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи» ИУС 3-2013
Переиздание. Сентябрь 2018 г.
Оглавление
1 Область применения
2 Нормативные ссылки
3 Термины, определения и обозначения
3.1 Термины и определения
3.2 Обозначения
4 Общие положения
5 Математические объекты
5.1 Математические определения
5.2 Параметры цифровой подписи
5.3 Двоичные векторы
6 Основные процессы
6.1 Формирование цифровой подписи
6.2 Проверка цифровой подписи
Приложение А (справочное) Контрольные примеры
А.1 Пример 1
А.1.1 Параметры схемы цифровой подписи
А.1.2 Процесс формирования цифровой подписи (алгоритмI)
А.1.3 Процесс проверки цифровой подписи (алгоритм II)
А.2 Пример 2
А.2.1 Параметры схемы цифровой подписи
А.2.2 Процесс формирования цифровой подписи (алгоритм I)
А.2.3 Процесс проверки цифровой подписи (алгоритм II)
Библиография
| Дата введения | 01.01.2013 |
|---|---|
| Добавлен в базу | 01.09.2013 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Экология
Организации:
| 07.08.2012 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 215-ст |
|---|---|---|---|
| Разработан | Центр защиты информации и специальной связи ФСБ России | ||
| Разработан | ОАО ИнфоТеКС | ||
| Издан | Стандартинформ | 2013 г. | |
| Издан | Стандартинформ | 2018 г. |
Information technology. Cryptographic data security. Generation and verification processes of electronic digital signature
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11
стр. 12
стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
ГОСТР
34.10-
2012
НАЦИОНАЛЬНЫЙ
СТАНДАРТ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
Информационная технология
КРИПТОГРАФИЧЕСКАЯ ЗАЩИТА ИНФОРМАЦИИ
Процессы формирования и проверки электронной цифровой подписи
Издание официальное
Москва
Стандартинформ
2013
ГОСТ Р 34.10-2012Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации — ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 РАЗРАБОТАН Центром защиты информации и специальной связи ФСБ России с участием Открытого акционерного общества «Информационные технологии и коммуникационные системы» (ОАО «ИнфоТеКС»)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК26 «Криптографическая защита информации»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 7 августа 2012 г. № 215-ст
4 ВЗАМЕН ГОСТ Р 34.10-2001
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
© Стандартинформ, 2013
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
ГОСТ Р 34.10-20126.1 Формирование цифровой подписи
Для получения цифровой подписи под сообщением М е V* необходимо выполнить следующие действия (шаги) по алгоритму I: _
Шаг 1 — вычислить хэш-код сообщения М: h = h(M). (13)
(14)
Шаг 2 — вычислить целое число а, двоичным представлением которого является вектор h, и определить
е (mod q).
Если е = 0, то определить е = 1.
Шаг 3 — сгенерировать случайное (псевдослучайное) целое число к, удовлетворяющее неравенству
0 <k<q. (15)
Шаг 4 — вычислить точку эллиптической кривой С = кР и определить
r = xc (mod q), (16)
где хс — х-координата точки С.
(17)
Если г= 0, то вернуться к шагу 3. Шаг 5 — вычислить значение
s = {rd + /re)(mod q).
Если s = 0, то вернуться к шагу 3.
Шаг 6 — вычислить двоичные векторы г и s, соответствующие г и s, и определить цифровую подпись С, = r||s как конкатенацию двух двоичных векторов.
Исходными данными этого процесса являются ключ подписи d и подписываемое сообщение М, а выходным результатом — цифровая подпись^.
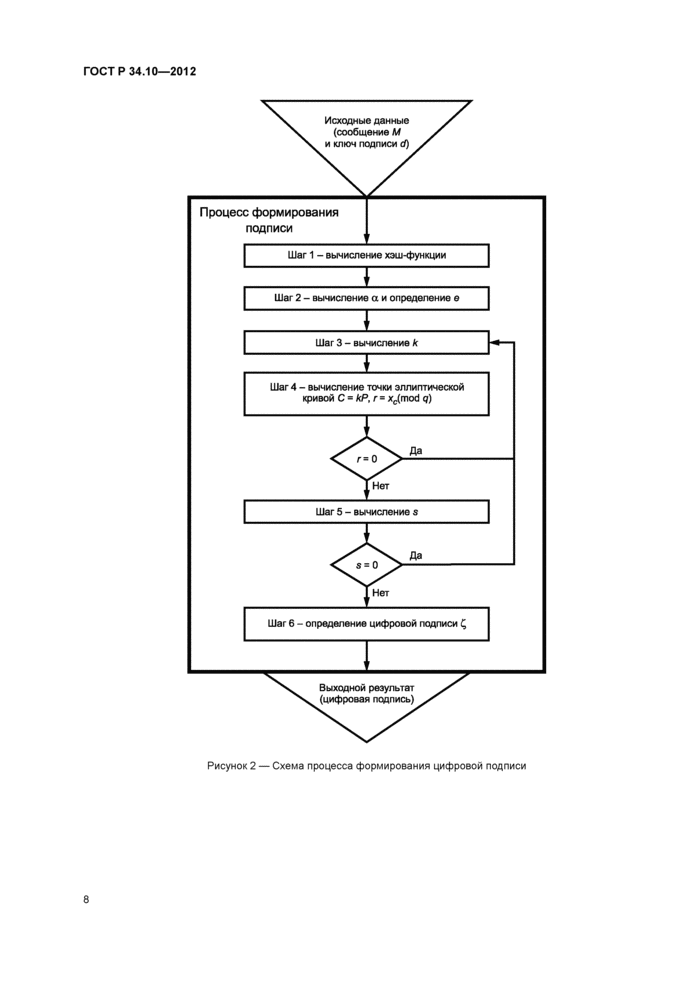
Схема процесса формирования цифровой подписи приведена на рисунке 2.
7
ГОСТ P 34.10—2012
Шаг 4 - вычисление точки эллиптической кривой С = кР, г = xc(mod q)
|
Да |
Шаг 5 - вычисление s
|
Да |
|
Шаг 6 - определение цифровой подписи С, | |||
|
Рисунок 2 — Схема процесса формирования цифровой подписи |
8
ГОСТ P 34.10—20126.2 Проверка цифровой подписи
Для проверки цифровой подписи £ под полученным сообщением М необходимо выполнить следующие действия (шаги) по алгоритму II:
Шаг 1 — по полученной подписи С, вычислить целые числа г и s. Если выполнены неравенства 0 < г < q, 0 < s < q, то перейти к следующему шагу. В противном случае подпись неверна.
Шаг 2 — вычислить хэш-код полученного сообщения М\
h=h(M). (18)
Шаг 3 — вычислить целое число а, двоичным представлением которого является вектор h, и определить
e^a(modq). (19)
Если е = 0, то определить е = 1.
Шаг 4 — вычислить значение v = е-1 (mod q). (20)
Шаг 5 — вычислить значения
z.| ее sv (mod q), z2 = -rv (mod q). (21)
Шаг 6 — вычислить точку эллиптической кривой С = глР + z2Q и определить
R = хс (mod q), (22)
где хс — х-координата точки С.
Шаг 7 — если выполнено равенство R = г, то подпись принимается, в противном случае — подпись неверна.
Исходными данными этого процесса являются подписанное сообщение М, цифровая подпись С, и ключ проверки подписи Q, а выходным результатом — свидетельство о достоверности или ошибочности данной подписи.
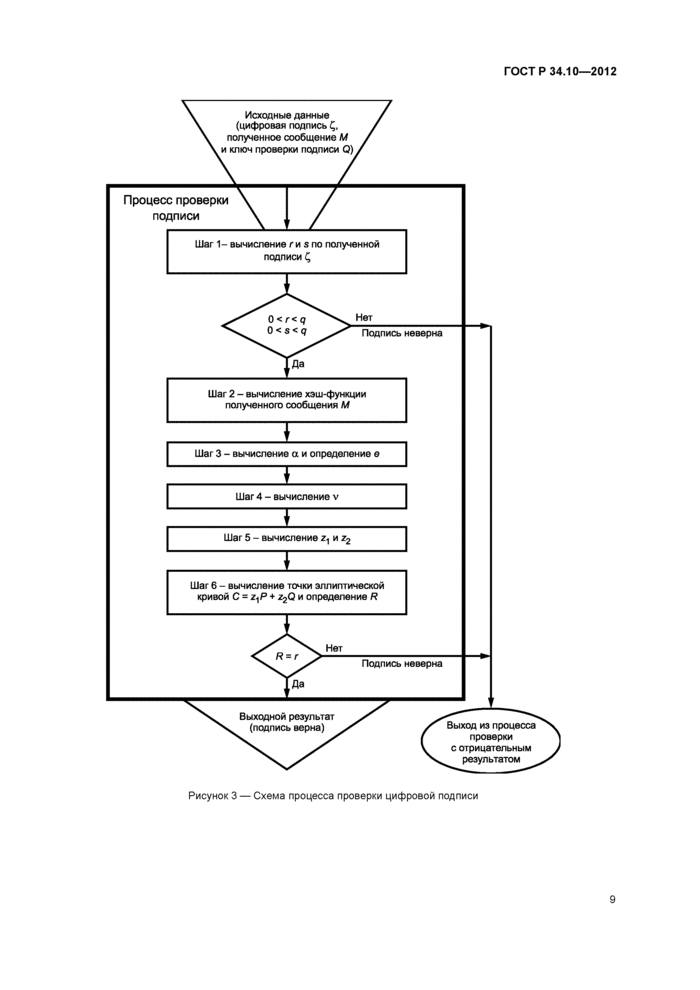
Схема процесса проверки цифровой подписи приведена на рисунке 3.
9
ГОСТ P 34.10—2012
|
Рисунок 3 — Схема процесса проверки цифровой подписи |
10
ГОСТ Р 34.10-2012Приложение А (справочное)Контрольные примеры
Контрольные примеры
Приводимые ниже значения параметров р, a, b, т, q, Р, а также значения ключей подписи и проверки подписи d и Q рекомендуется использовать только для проверки корректной работы конкретной реализации алгоритмов, описанных в настоящем стандарте.
Все числовые значения приведены в десятичной и шестнадцатеричной записи. Нижний индекс в записи числа обозначает основание системы счисления. Символ «\\» обозначает перенос числа на новую строку. Например, запись
12345W
6789010
499602D216
представляет целое число 1234567890 в десятичной и шестнадцатеричной системах счисления соответственно. А.1 Пример 1
А. 1.1 Параметры схемы цифровой подписи
Для формирования и проверки цифровой подписи должны быть использованы следующие параметры (см. 5.2).
А.1.1.1 Модуль эллиптической кривой
В данном примере параметру р присвоено следующее значение:
р = 57896044618658097711785492504343953926U 63499233282028201972879200395656482104110 р = 800000000000000000000000000000000000000000000000000000000000043116.
А.1.1.2 Коэффициенты эллиптической кривой
В данном примере параметры а и b принимают следующие значения:
а = 710, а = 716,
Ь = 43308876546767276905765904595650931995W 94211179445103958325296884203384958041410,
Ь = 5FBFF498AA938CE739B8E022FBAFEF40563F6E6A3472FC2A514C0CE9DAE23B7E16.
А.1.1.3 Порядок группы точек эллиптической кривой
В данном примере параметр т принимает следующее значение:
т= 5789604461865809771178549250434395392W 708293458372545062238097359213763106961910, т = 8000000000000000000000000000000150FE8A1892976154C59CFC193ACCF5B3,6.
А.1.1.4 Порядок циклической подгруппы группы точек эллиптической кривой
В данном примере параметр q принимает следующее значение:
q= 5789604461865809771178549250434395392W 708293458372545062238097359213763106961910, q = 8000000000000000000000000000000150FE8A1892976154C59CFC193ACCF5B316.
А. 1.1.5 Коэффициенты точки эллиптической кривой
В данном примере координаты точки Р принимают следующие значения:
хр = 2-ю’
х = 216,
Ур = 401897405653903750з'з354494229370597\\ 7563573938990554508069097936521343156628010, ур = 8E2A8A0E65147D4BD6316030E16D19W C85C97F0A9CA267122B96ABBCEA7E8FC816.
А.1.1.6 Ключ подписи
В данном примере считается, что пользователь обладает следующим ключом подписи d:
d= 554411960653632461263556241303241831W 9657670922234001657210809775000609752554410, d = 7A929ADE789BB9BE10ED359DD39A72CW 11В60961F49397EEE1D19СЕ9891ЕСЗВ2816.
11
ГОСТ P 34.10—2012А.1.1.7 Ключ проверки подписи
В данном примере считается, что пользователь обладает ключом проверки подписи Q, координаты которого имеют следующие значения:
х = 57520216126176808443631405023338071 \\
17663010490631363218289674134220660485940310, xq = 7F2B49E270DB6D90D8595BEC458B5W 0С58585ВА1D4E9B788F6689DBD8E56FD80B1S, у =17614944419213781543809391949654080W 03194266204536363926070984785943828676399410, у = 26F1B489D6701DD185C8413A977B3W CBBAF64D1C593D26627DFFB101 A87FF77DA,6.
А. 1.2 Процесс формирования цифровой подписи (алгоритм I)
Пусть после выполнения шагов 1—3 по алгоритму I (см. 6.1) были получены следующие числовые значения:
е = 2079889367447645201713406156150827013\\ 063714251537965328995261725266146887242110, е = 2DFBC1B372D89A1188C09C52E0EEW С61FCE52032AB1022E8E67ECE6672B043EE516, к= 538541376773484637314038411479966192U 4150400343430202071296083852889319623339510, к = 77105C9B20BCD3122823C8CF6FCCW 7B956DE33814E95B7FE64FED924594DCEAB316.
При этом кратная точка С - кР имеет координаты:
хс = 297009809158179528743712049839382569W 9042275210799431965163268798205921093339510, хс = 41AA28D2F1AB148280CD9ED56FEDW А41974053554A42767B83AD043FD39DC049316, ус = 328425352786846634770946653225170845W 0680472103245454326813285455653927406091010, ус = 489С375А9941A3049E33B34361DDW 204172AD98C3E5916DE27695D22A61FAE46E16.
Параметр r= хс (mod q) принимает значение:
г=297009809158179528743712049839382569W 9042275210799431965163268798205921093339510, г = 41AA28D2F1AB148280CD9ED56FEDW А41974053554A42767B83AD043FD39DC049316.
Параметр s = (rd + ке) (mod q) принимает значение:
s = 57497340027008465417892531001914703W
8455227042649098563933718999175515839552.0,
s = 1456C64BA4642A1653C235A98A60249BCD6D3F746B631DF928014F6C5BF9C4016.
А. 1.3 Процесс проверки цифровой подписи (алгоритм II)
Пусть после выполнения шагов 1—3 по алгоритму II (см. 6.2) были получены следующие числовые значения:
е = 2079889367447645201713406156150827013\\ 063714251537965328995261725266146887242110.
е = 2DFBC1B372D89A1188C09C52E0EEW C61FCE52032AB1022E8E67ECE6672B043EE516.
При этом параметр и = e_1 (mod q) принимает значение:
и = 176866836059344686773017138249002685W
62746883080675496715288036572431145718978.0, и = 271A4EE429F84EBC423E388964555BBW 29D3BA53C7BF945E5FAC8F381706354C216.
Параметры z= sv (mod q) и z2 =-rv (mod q) принимают значения:
z., = 376991675009019385568410572935126561W 0884134519049194261930453241274372099975^ 0, z, = 5358F8FFB38F7C09ABC782A2DF2AW 3927DA4077D07205F763682F3A76C9019B4F16, z2 = 141719984273434721125159179695007657W 692466558389728621144999326533336710922110, z2 = 3221B4FBBF6D101074EC14AFAC2D4F7W EFAC4CF9FEC1 ED11BAE336D27D52766516.
12
ГОСТ Р 34.10-2012
Точка С = zf + z2Q имеет координаты:
хс = 2970098091581795287437120498393825699W 042275210799431965163268798205921093339510, хс = 41AA28D2F1AB148280CD9ED56FEDW A41974053554A42767B83AD043FD39DC049316, ус = 3284253527868466347709466532251708450W 680472103245454326813285455653927406091010, ус = 489С375А9941A3049E33B34361DDW 204172AD98C3E5916DE27695D22A61FAE46E16.
Тогда параметр R = хс (mod q) принимает значение:
R=2970098091581795287437120498393825699W 042275210799431965163268798205921093339510,
R = 41AA28D2F1AB148280CD9ED56FEDW A41974053554A42767B83AD043FD39DC049316.
Поскольку выполнено равенство R = г, то цифровая подпись принимается.
А.2 Пример 2
А.2.1 Параметры схемы цифровой подписи
Для формирования и проверки цифровой подписи должны быть использованы следующие параметры (см.
5.2).
А.2.1.1 Модуль эллиптической кривой
В данном примере параметру р присвоено следующее значение:
р= 36239861022290036359077887536838743060213209255346786050W 8654615045085616662400248258848202227149685402509082360305W 873516373426382237196498722858290737240^ 0, р = 4531ACD1FE0023C7550D267B6B2FEE80922B14B2FFB90F04D4EB7C09B5D2D15DW F1D852741AF4704A0458047E80E4546D35B8336FAC224DD81664BBF528BE6373,6.
А.2.1.2 Коэффициенты эллиптической кривой
В данном примере параметры а и b принимают следующие значения:
а - 710, а = 716,
b= 1518655069210828534508950034714043154928747527740206436W 1940188233528099824437937328297569147859746748660416053978836775W 9662632641399013695904743581182639610,
Ь = 1CFF0806A31116DA29D8CFA54E57EB748BC5F377E49400FDD788B649ECA1AC4W 361834013B2AD7322480A89CA58E0CF74BC9E540C2ADD6897FAD0A3084F302ADG|6.
А.2.1.3 Порядок группы точек эллиптической кривой
В данном примере параметр т принимает следующее значение:
т = 36239861022290036359077887536838743060213209255346786050865461W 50450856166623969164898305032863068499961404079437936585455865192212\\
97073480881261812061974310, т = 4531ACD1FE0023C7550D267B6B2FEE80922B14B2FFB90F04D4EB7C09B5D2D15DW A82F2D7ECB1DBAC719905C5EECC423F1D86E25EDBE23C595D644AAF187E6E6DF16.
А.2.1.4 Порядок циклической подгруппы группы точек эллиптической кривой
В данном примере параметр q принимает следующее значение:
q= 36239861022290036359077887536838743060213209255346786050865461W 50450856166623969164898305032863068499961404079437936585455865192212\\
97073480881261812061974310, q = 4531ACD1FE0023C7550D267B6B2FEE80922B14B2FFB90F04D4EB7C09B5D2D15DW A82F2D7ECB1DBAC719905C5EECC423F1D86E25EDBE23C595D644AAF187E6E6DF16.
А.2.1.5 Коэффициенты точки эллиптической кривой
В данном примере координаты точки Р принимают следующие значения:
хр= 19283569440670228493993094012431375989977866354595079743570754913077665W 9268583544106555768100318487481965800490321233288425233583025072952763238W
349357327410,
Хр = 24D19CC64572EE30F396BF6EBBFD7A6C5213B3B3D7057CC825F91093A68CD762W FD60611262CD838DC6B60AA7EEE804E28BC849977FAC33B4B530F1 В120248А9А,6,
Ур =22887286933719728599700121555294784163535623273295061803W 144974259311028603015728141419970722717088070665938506503341523818\\
13
ГОСТ Р 34.10-2012
5734779888586480760509872401385410, ур = 2ВВ312A43BD2CE6E0D020613C857ACDDCFBF061Е91E5F2C3F32447C259F39B2W С83АВ156D77F1496BF7EB3351 El EE4E43DC1A18В91B24640B6DBB92CB1ADD371 Е,6.
А.2.1.6 Ключ подписи
В данном примере считается, что пользователь обладает следующим ключом подписи d:
d=610081804136373098219538153239847583006845519069531562982388135W 35489060630178225538360839342337237905766552759511682730702504645883W
74407661211804668758601О, d = BA6048AADAE241BA40936D47756D7C93091А0Е8514669700ЕЕ7508Е508В102072W E8123B2200A0563322DAD2827E2714A2636B7BFD18AADFC62967821FA18DD4le.
А.2.1.7 Ключ проверки подписи
В данном примере считается, что пользователь обладает ключом проверки подписи Q, координаты которого
имеют следующие значения:
xq = 9095468530025365965566907686698303100069292725465562815963W 72965370312498563182320436892870052842808608262832456858223580W 71378029071798685586343343115056110, xq = 115DC5BC96760C7B48598D8AB9E740D4C4A85A65BE33C1815B5C320C854621DW D5A515856D13314AF69BC5B924C8B4DDFF75C45415C1D9DD9DD33612CD530EFE116. yq=29214572033744256206324497342484154556407008235594887051648958W 37509539134297327397380287741428246088626609329139441895016863758W 98410632660057247682237207610, yq = 37C7C90CD40B0F5621DC3AC1В751CFA0E2634FA0503B3D52639F5D7FB72AFD6W 1ЕА199441D943FFE7F0C70A2759A3CDB84C114Е1F9339FDF27F35ECA93677BEEC16.
A.2.2 Процесс формирования цифровой подписи (алгоритм I)
Пусть после выполнения шагов 1—3 по алгоритму! (см. 6.1) были получены следующие числовые значения:
е = 2897963881682868575562827278553865049173745197871825199562947W 4190413889509705366611095534999542487330887197488445389646412816544W 6351329697382770627204596410, е = 3754F3CFACC9E0615C4F4A7C4D8DAB531B09B6F9C170C533A71D147035B0C591W 7184EE536593F4414339976C647C5D5A407ADEDB1D560C4FC6777D2972075B8Cie, к= 1755163560258504995406282799211252803334510317477377916502W 081442431820570750344461029867509625089092272358661268724735168078105417W
4752971030987995863294510, к = 359E7F4B1410FEACC570456C6801496946312120B39D019D455986E364F3W 65886748ED7A44B3E794434006011842286212273A6D14CF70EA3AF71BB1AE679F116.
При этом кратная точка С = кР имеет координаты:
хс = 24892044770313492650728646430321477536674513192821314440274986373W 576110928102217951018714129288237168059598287083302842436534530853W 2200444244253415176146210, хс = 2F86FA60A081091A23DD795E1ЕЗС689ЕЕ512A3C82EE0DCC2643C78EEA8FCACW D35492558486B20F1С9ЕС197C90699850260C93BCBCD9C5C3317Е19344Е173АЕ36,6, ус = 77017388992899183604784479878096044168206263187609613767394680150U 24422293532765176528442837832456936422662546513702148162933079517\\
0843005015210864150831010, ус = EB488140F7E2F4E35CF220BDBC75AE44F26F9C7DF52E82436BDE80A91831DA27W C8100DAA876F9ADC0D28A82DD3826D4DC7F92E471DA23E55E0EBB3927C85BD616.
Параметр г = хс (mod q) принимает значение:
г = 24892044770313492650728646430321477536674513192821314440274986373W 576110928102217951018714129288237168059598287083302842436534530853W 2200444244253415176146210, г = 2F86FA60A081091A23DD795E1ЕЗС689ЕЕ512A3C82EE0DCC2643C78EEA8FCACW D35492558486B20F1С9ЕС197C90699850260C93BCBCD9C5C3317Е19344Е173АЕ36,6.
Параметр s = (rd + /се) (mod q) принимает значение:
s = 8645232217076695190388492973829369170750237358484315799195987U 99313385180564748877195639672460179421760770893278030956807690115\\ 82270990385368283183515937010, s = 1081B394696FFE8E6585E7A9362D26B6325F56778AADBC081C0BFBE933D52FF58W 23CE288E8C4F362526080DF7F70CE406A6EEB1F56919CB92A9853BDE73E5B4A,6.
14
ГОСТ P 34.10—2012А.2.3 Процесс проверки цифровой подписи (алгоритм II)
Пусть после выполнения шагов 1—3 по алгоритму II (см. 6.2) было получено следующее числовое значение:
е = 2897963881682868575562827278553865049173745197871825199562947W 4190413889509705366611095534999542487330887197488445389646412816544W
63513296973827706272045964., 0, е = 3754F3CFACC9E0615C4F4A7C4D8DAB531B09B6F9C170C533A71D147035B0C591W 7184EE536593F4414339976C647C5D5A407ADEDB1D560C4FC6777D2972075B8C16.
При этом параметр v= е-1 (mod q) принимает значение:
v= 255694215394605222266074084316408615387769223440078319114692849W 356194345732344708924001925205698280688153534004145821243990606136W 707223818593481596025267110, v= 30D212A9E25D1A80A0F238532CADF3E64D7EF4E782B6AD140AAF8BBD9BB4729W 84595EEC87B2F3448A1999D5F0A6DE0E14A55AD875721EC8CFD504000B3A840FF16.
Параметры z1 = si/(mod q) и z2 = -n/(mod q) принимают значения:
z., = 3206470827336768629686907101873475250343306448089030311214484W 385872743205045180345208826552901003496732941049780357793541942055W 60008495619817370719790257510, z., = 3D38E7262D69BB2AD24DD81EEA2F92E6348D619FA45007B175837CF13B026079W 051A48A1A379188F37BA46CE12F7207F2A8345459FF960E1EBD5B4F2A34A6EEF16, z2=13667709118340031081429778480218475973204553475356412734827W 320820470283421680060312618142732308792036907264486312226797437575W 6163726695805680585960300820310, z2= 1A18A31602E6EAC0A9888C01941082AEFE296F840453D2603414C2A16EB6FC529W D8D8372E50DC49D6C612CE1FF65BD58E1D2029F22690438CC36A76DDA444ACB16.
Точка C = zJP + z2Q имеет координаты:
xc = 2489204477031349265072864643032147753667451319282131444027498637W 3576110928102217951018714129288237168059598287083302842436534530853W
22004442442534151761462., 0, xc = 2F86FA60A081091A23DD795E1E3C689EE512A3C82EE0DCC2643C78EEA8FCACW D35492558486B20F1C9EC197C90699850260C93BCBCD9C5C3317E19344E173AE3616, yc = 7701738899289918360478447987809604416820626318760961376739468015\\ 0244222935327651765284428378324569364226625465137021481629330795170W
843005015210864150831010, yc= EB488140F7E2F4E35CF220BDBC75AE44F26F9C7DF52E82436BDE80A91831DA27W C8100DAA876F9ADC0D28A82DD3826D4DC7F92E471DA23E55E0EBB3927C85BD616.
Тогда параметр R = xc (mod q) принимает значение:
R=24892044770313492650728646430321477536674513192821314440274986W 37357611092810221795101871412928823716805959828708330284243653453085W 32200444244253415176146210,
R = 2F86FA60A081091A23DD795E1E3C689EE512A3C82EE0DCC2643C78EEA8FCACW D35492558486B20F1C9EC197C90699850260C93BCBCD9C5C3317E19344E173AE3616.
Поскольку выполнено равенство R = г, то цифровая подпись принимается.
15
Библиография1
[1] ИСО 2382-2:1976
(ISO 2382-2:1976)
[2] ИСО/МЭК 9796-2:2010
(ISO/IEC 9796-2:2010)
[3] ИСО/МЭК 9796-3:2006
(ISO/IEC 9796-3:2006)
[4] ИСО/МЭК 14888-1:2008 (ISO/IEC 14888-1:2008)
[5] ИСО/МЭК 14888-2:2008 (ISO/IEC 14888-2:2008)
[6] ИСО/МЭК 14888-3:2006 (ISO/IEC 14888-3:2006)
[7] ИСО/МЭК 14888-3:2006/Изм. 1:2010
(ISO/IEC 14888-3:2006/Amd 1:2010)
[8] ИСО/МЭК 10118-1:2000
(ISO/IEC 10118-1:2000)
[9] ИСО/МЭК 10118-2:2010
(ISO/IEC 10118-2:2010)
[10] ИСО/МЭК 10118-3:2004 (ISO/IEC 10118-3:2004)
[11] ИСО/МЭК 10118-4:1998 (ISO/IEC 10118-4:1998)
[1] ИСО 2382-2:1976
(ISO 2382-2:1976)
[2] ИСО/МЭК 9796-2:2010
(ISO/IEC 9796-2:2010)
[3] ИСО/МЭК 9796-3:2006
(ISO/IEC 9796-3:2006)
[4] ИСО/МЭК 14888-1:2008 (ISO/IEC 14888-1:2008)
[5] ИСО/МЭК 14888-2:2008 (ISO/IEC 14888-2:2008)
[6] ИСО/МЭК 14888-3:2006 (ISO/IEC 14888-3:2006)
[7] ИСО/МЭК 14888-3:2006/Изм. 1:2010
(ISO/IEC 14888-3:2006/Amd 1:2010)
[8] ИСО/МЭК 10118-1:2000
(ISO/IEC 10118-1:2000)
[9] ИСО/МЭК 10118-2:2010
(ISO/IEC 10118-2:2010)
[10] ИСО/МЭК 10118-3:2004 (ISO/IEC 10118-3:2004)
[11] ИСО/МЭК 10118-4:1998 (ISO/IEC 10118-4:1998)
Системы обработки информации. Словарь. Часть 2. Арифметические и логические операции
(Data processing — Vocabulary — Part 2: Arithmetic and logic operations) Информационные технологии. Методы обеспечения безопасности. Схемы цифровой подписи, обеспечивающие восстановление сообщений. Часть 2. Механизмы на основе целочисленной факторизации
(Information technology — Security techniques — Digital signature schemes giving message recovery — Part 2: Integer factorization based mechanisms) Информационные технологии. Методы обеспечения безопасности. Схемы цифровой подписи, обеспечивающие восстановление сообщений. Часть 3. Механизмы на основе дискретного логарифма
(Information technology — Security techniques — Digital signature schemes giving message recovery — Part 3: Discrete logarithm based mechanisms) Информационные технологии. Методы защиты. Цифровые подписи с приложением. Часть 1. Общие положения
(Information technology — Security techniques — Digital signatures with
appendix — Part 1: General)
Информационные технологии. Методы защиты. Цифровые подписи с приложением. Часть 2. Механизмы, основанные на разложении на множители (Information technology — Security techniques — Digital signatures with
appendix — Part 2: Integer factorization based mechanisms)
Информационные технологии. Методы защиты. Цифровые подписи с приложением. Часть 3. Механизмы на основе дискретного логарифма (Information technology — Security techniques — Digital signatures with appendix — Part 3: Discrete logarithm based mechanisms)
Информационные технологии. Методы защиты. Цифровые подписи с приложением. Часть 3. Механизмы на основе дискретного логарифма. Изменение 1. Алгоритм русской цифровой подписи эллиптической кривой, алгоритм цифровой подписи Шнора, алгоритм цифровой подписи Шнора для эллиптической кривой и полный алгоритм цифровой подписи Шнора для эллиптической кривой (Information technology — Security techniques — Digital signatures with appendix — Part 3: Discrete logarithm based mechanisms. Ammendment 1. Elliptic Curve Russian Digital Signature Algorithm, Schnorr Digital Signature Algorithm, Elliptic Curve Schnorr Digital Signature Algorithm, and Elliptic Curve Full Schnorr Digital Signature Algorithm)
Информационные технологии. Методы защиты информации. Хэш-функции. Часть 1. Общие положения
(Information technology — Security techniques — Hash-functions — Part 1: General) Информационные технологии. Методы защиты информации. Хэш-функции. Часть 2. Хэш-функции с использованием алгоритма шифрования n-битными блоками
(Information technology — Security techniques — Hash-functions — Part 2:
Hash-functions using an n-bit block cipher)
Информационные технологии. Методы защиты информации. Хэш-функции. Часть 3. Выделенные хэш-функции
(Information technology — Security techniques — Hash-functions — Part 3:
Dedicated hash-functions)
Информационные технологии. Методы защиты информации. Хэш-функции. Часть 4. Хэш-функции с применением арифметики в остаточных классах (Information technology — Security techniques — Hash-functions — Part 4:
Hash-functions using modular arithmetic)
ГОСТ P 34.10—2012Содержание
1 Область применения............................................1
2 Нормативные ссылки............................................1
3 Термины, определения и обозначения..................................1
3.1 Термины и определения.......................................1
3.2 Обозначения..............................................3
4 Общие положения.............................................3
5 Математические объекты.........................................4
5.1 Математические определения....................................4
5.2 Параметры цифровой подписи....................................5
5.3 Двоичные векторы...........................................6
6 Основные процессы............................................6
6.1 Формирование цифровой подписи..................................7
6.2 Проверка цифровой подписи.....................................9
Приложение А (справочное) Контрольные примеры...........................11
А.1 Пример 1...............................................11
А.1.1 Параметры схемы цифровой подписи...........................11
А.1.2 Процесс формирования цифровой подписи (алгоритм I).................12
А.1.3 Процесс проверки цифровой подписи (алгоритм II)....................12
А.2 Пример 2...............................................13
А.2.1 Параметры схемы цифровой подписи...........................13
А.2.2 Процесс формирования цифровой подписи (алгоритм I).................14
А.2.3 Процесс проверки цифровой подписи (алгоритм II)....................15
Библиография................................................16
УДК 681.3.06:006.354 ОКС 35.040 ОКСТУ 5001 П85
Ключевые слова: обработка данных, передача данных, обмен информацией, сообщения, цифровые подписи, защита информации, формирование цифровой подписи, проверка цифровой подписи
17
Введение
Настоящий стандарт содержит описание процессов формирования и проверки электронной цифровой подписи (ЭЦП), реализуемой с использованием операций в группе точек эллиптической кривой, определенной над конечным простым полем.
Необходимость разработки настоящего стандарта вызвана потребностью в реализации электронной цифровой подписи разной степени стойкости в связи с повышением уровня развития вычислительной техники. Стойкость электронной цифровой подписи основывается на сложности вычисления дискретного логарифма в группе точек эллиптической кривой, а также на стойкости используемой хэш-функции по ГОСТ Р 34.11-2012.
Настоящий стандарт разработан с учетом терминологии и концепций международных стандартов ИСО 2382-2 [1], ИСО/МЭК 9796 [2]—[3], ИСО/МЭК 14888 [4]—[7] и ИСО/МЭК 10118 [8]—[11].
IV
ГОСТ P 34.10—2012
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИИнформационная технология КРИПТОГРАФИЧЕСКАЯ ЗАЩИТА ИНФОРМАЦИИ Процессы формирования и проверки электронной цифровой подписи
Information technology. Cryptographic data security.
Generation and verification processes of electronic digital signature
Дата введения — 2013—01—01
1 Область применения
Настоящий стандарт определяет схему электронной цифровой подписи (ЭЦП) (далее — цифровая подпись), процессы формирования и проверки цифровой подписи под заданным сообщением (документом), передаваемым по незащищенным телекоммуникационным каналам общего пользования в системах обработки информации различного назначения.
Внедрение цифровой подписи на основе настоящего стандарта повышает по сравнению с ранее действовавшей схемой цифровой подписи уровень защищенности передаваемых сообщений от подделок и искажений.
Настоящий стандарт рекомендуется применять при создании, эксплуатации и модернизации систем обработки информации различного назначения.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ Р 34.11-2012 Информационная технология. Криптографическая защита информации. Функция хэширования
Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины, определения и обозначения
3.1 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1.1 _
дополнение (appendix): Строка бит, формируемая из цифровой подписи и произвольного текстового поля.
[ИСО/МЭК 14888-1:2008, [4]]
3.1.2 _
ключ подписи (signature key): Элемент секретных данных, специфичный для субъекта и используемый только данным субъектом в процессе формирования цифровой подписи.
[ИСО/МЭК 14888-1:2008, [4]]
Издание официальное
3.1.3_
ключ проверки подписи (verification key): Элемент данных, математически связанный с ключом подписи и используемый проверяющей стороной в процессе проверки цифровой подписи.
[ИСО/МЭК 14888-1:2008, [4]]
3.1.4
параметр схемы ЭЦП (domain parameter): Элемент данных, общий для всех субъектов схемы цифровой подписи, известный или доступный всем этим субъектам.
[ИСО/МЭК 14888-1:2008, [4]]
3.1.5
подписанное сообщение (signed message): Набор элементов данных, состоящий из сообщения и (дополнения, являющегося частью сообщения.
[ИСО/МЭК 14888-1:2008, [4]]
3.1.6
последовательность псевдослучайных чисел (pseudo-random number sequence): Последовательность чисел, полученная в результате выполнения некоторого арифметического (вычислительного) процесса, используемая в конкретном случае вместо последовательности случайных чисел.
[ИСО 2382-2:1976, [1]]
3.1.7
последовательность случайных чисел (random number sequence): Последовательность чисел, каждое из которых не может быть предсказано (вычислено) только на основе знания предшествующих ему чисел данной последовательности.
[ИСО 2382-2:1976, [1]]
3.1.8
процесс проверки подписи (verification process): Процесс, в качестве исходных данных которого используются подписанное сообщение, ключ проверки подписи и параметры схемы ЭЦП, результатом которого является заключение о правильности или ошибочности цифровой подписи.
[ИСО/МЭК 14888-1:2008, [4]]
3.1.9
процесс формирования подписи (signature process): Процесс, в качестве исходных данных которого используются сообщение, ключ подписи и параметры схемы ЭЦП, а в результате формируется цифровая подпись.
[ИСО/МЭК 14888-1:2008, [4]]
3.1.10 свидетельство (witness): Элемент данных, представляющий соответствующее доказательство достоверности (недостоверности) подписи проверяющей стороне.
случайное число (random number): Число, выбранное из определенного набора чисел таким образом, что каждое число из данного набора может быть выбрано с одинаковой вероятностью.
[ИСО 2382-2:1976, [1]]
3.1.11
сообщение (message): Строка бит произвольной конечной длины. [ИСО/МЭК 14888-1:2008, [4]]
сообщение (message): Строка бит произвольной конечной длины. [ИСО/МЭК 14888-1:2008, [4]]
3.1.12
хэш-код (hash-code): Строка бит, являющаяся выходным результатом хэш-функции. [ИСО/МЭК 14888-1:2008, [4]]
3.1.13
2
ГОСТ P 34.10—2012
3.1.14 _
хэш-функция (collision-resistant hash-function): Функция, отображающая строки бит в строки бит фиксированной длины и удовлетворяющая следующим свойствам:
1) по данному значению функции сложно вычислить исходные данные, отображаемые в это значение;
2) для заданных исходных данных сложно вычислить другие исходные данные, отображаемые в то же значение функции;
3) сложно вычислить какую-либо пару исходных данных, отображаемых в одно и то же значение.
[ИСО/МЭК 14888-1:2008, [4]]_
Примечания
1 Применительно к области электронной цифровой подписи свойство по перечислению 1) подразумевает, что по известной электронной цифровой подписи невозможно восстановить исходное сообщение; свойство по перечислению 2) подразумевает, что для заданного подписанного сообщения трудно подобрать другое (фальсифицированное) сообщение, имеющее ту же электронную цифровую подпись; свойство по перечислению 3) подразумевает, что трудно подобрать какую-либо пару сообщений, имеющих одну и ту же подпись.
2 В настоящем стандарте в целях сохранения терминологической преемственности с действующими отечественными нормативными документами и опубликованными научно-техническими изданиями установлено, что термины «хэш-функция», «криптографическая хэш-функция», «функция хэширования» и «криптографическая функция хэширования» являются синонимами.
[электронная цифровая] подпись (signature); ЭЦП: Строка бит, полученная в результате процесса формирования подписи.
[ИСО/МЭК 14888-1:2008, [4]]
3.1.15
Примечания
1 Строка бит, являющаяся подписью, может иметь внутреннюю структуру, зависящую от конкретного механизма формирования подписи.
2 В настоящем стандарте в целях сохранения терминологической преемственности с действующими отечественными нормативными документами и опубликованными научно-техническими изданиями установлено, что термины «электронная подпись», «цифровая подпись» и «электронная цифровая подпись» являются синонимами.
3.2 Обозначения
В настоящем стандарте применены следующие обозначения:
Vt — множество всех двоичных векторов длиной / бит;
V* — множество всех двоичных векторов произвольной конечной длины;
Z — множество всех целых чисел;
р — простое число, р > 3;
Fp — конечное простое поле, представляемое как множество из р целых чисел
{0,1,...,р-1};
b(mod р) — минимальное неотрицательное число, сравнимое с b по модулю р;
М — сообщение пользователя, Af е V*;
(/?i 11 /?2) — конкатенация (объединение) двух двоичных векторов;
а, Ь — коэффициенты эллиптической кривой; т — порядок группы точек эллиптической кривой;
q — порядок подгруппы группы точек эллиптической кривой;
О — нулевая точка эллиптической кривой;
Р — точка эллиптической кривой порядка д;
d — целое число — ключ подписи;
Q — точка эллиптической кривой — ключ проверки подписи;
Q — цифровая подпись под сообщением М.
4 Общие положения
Общепризнанная схема (модель) цифровой подписи (см. ИСО/МЭК 14888-1 [4]) охватывает следующие процессы:
- генерация ключей (подписи и проверки подписи);
3
- формирование подписи;
- проверка подписи.
В настоящем стандарте процесс генерации ключей (подписи и проверки подписи) не рассмотрен. Характеристики и способы реализации данного процесса определяются вовлеченными в него субъектами, которые устанавливают соответствующие параметры по взаимному согласованию.
Механизм цифровой подписи определяется посредством реализации двух основных процессов (см. раздел 6):
- формирование подписи (см. 6.1);
- проверка подписи (см. 6.2).
Цифровая подпись предназначена для аутентификации лица, подписавшего электронное сообщение. Кроме того, использование ЭЦП предоставляет возможность обеспечить следующие свойства при передаче в системе подписанного сообщения:
- осуществление контроля целостности передаваемого подписанного сообщения;
- доказательное подтверждение авторства лица, подписавшего сообщение;
- защита сообщения от возможной подделки.
Схематическое представление подписанного сообщения показано на рисунке 1.
| ||||||||||||
|
Рисунок 1 — Схема подписанного сообщения | ||||||||||||
Поле «Текст», показанное на данном рисунке и дополняющее поле «Цифровая подпись», может, например, содержать идентификаторы субъекта, подписавшего сообщение, и/или метку времени.
Установленная в настоящем стандарте схема цифровой подписи должна быть реализована с использованием операций группы точек эллиптической кривой, определенной над конечным простым полем, а также хэш-функции.
Криптографическая стойкость данной схемы цифровой подписи основывается на сложности решения задачи дискретного логарифмирования в группе точек эллиптической кривой, а также на стойкости используемой хэш-функции. Алгоритмы вычисления хэш-функции установлены в ГОСТ Р 34.11-2012.
Параметры схемы цифровой подписи, необходимые для ее формирования и проверки, определены в 5.2. В настоящем стандарте предусмотрена возможность выбора одного из двух вариантов требований к параметрам.
Настоящий стандарт не определяет процесс генерации параметров схемы цифровой подписи. Конкретный алгоритм (способ) реализации данного процесса определяется субъектами схемы цифровой подписи исходя из требований к аппаратно-программным средствам, реализующим электронный документооборот.
Цифровая подпись, представленная в виде двоичного вектора длиной 512 или 1024 бита, должна вычисляться с помощью определенного набора правил, изложенных в 6.1.
Набор правил, позволяющих принять либо отвергнуть цифровую подпись под полученным сообщением, установлен в 6.2.
5 Математические объекты
Для определения схемы цифровой подписи необходимо описать базовые математические объекты, используемые в процессах ее формирования и проверки. В данном разделе установлены основные математические определения и требования, предъявляемые к параметрам схемы цифровой подписи.
5.1 Математические определения
Эллиптической кривой Е, определенной над конечным простым полем Fp (где р > 3 — простое число), называется множество пар (х, у), х, y&Fp, удовлетворяющих уравнению
у2 =хз + ах + b (mod р), (1)
где a, b е Fp и 4а3 + 27Ь2 не сравнимо с нулем по модулю р.
4
ГОСТ P 34.10—2012
Инвариантом эллиптической кривой называется величина J(E), удовлетворяющая уравнению
л з
J(E) = 1728 —^-- (mod р). (2)
4а3 +21о
Пары (х, у), где х, у — элементы поля F , удовлетворяющие уравнению (1), называются «точками эллиптической кривой Е»; х и у — соответственно х- и у-координатами точки.
Точка эллиптической кривой обозначается Q(x, у) или просто Q. Две точки эллиптической кривой равны, если равны их соответствующие х- и у-координаты.
На множестве точек эллиптической кривой Е определена операция сложения, обозначаемая знаком «+». Для двух произвольных точек Q^x^ у.,) и Q2(x2, у2) эллиптической кривой Е рассматривают несколько случаев.
Для точек Q1 и <Э2, координаты которых удовлетворяют условию х1 ф х2, их суммой называется точка Q3(x3, уд), координаты которой определяются сравнениями
Jx3 = Х2 -X., -x2(modp), ^2)
|у3 = Х{х^ -x3)-y1(modp),
где X = ——— (mod р). х2 -х1
Если выполнены равенства х1 = х2 и у1 = у2 ф 0, то координаты точки Q3 определяются следующим образом:
1х3 = Х2 -гх^тоdp), (4)
[Уз = M*i ~хз) -y-i(modp),
. Зх? + а , .
где X = —1-(mod р).
2yi
Если выполнены условия х1 = х2 и y1 =-y2(mod р), то сумма точек Q1 и Q2 называется нулевой точкой О без определения ее х- и у-координат. В этом случае точка <Э2 называется отрицанием точки Для нулевой точки О выполнены равенства
Q + О = О + Q = Q, (5)
где Q — произвольная точка эллиптической кривой Е.
Относительно введенной операции сложения множество точек эллиптической кривой Е вместе с нулевой точкой образуют конечную абелеву (коммутативную) группу порядка т, для которого выполнено неравенство
р + 1 -2-sfp <т<р + 1 + 27р- (6)
Точка Q называется «точкой кратности к» или просто «кратной точкой эллиптической кривой Е», если для некоторой точки Р выполнено равенство
Q = Р + ... + Р= кР. (7)
к '
5.2 Параметры цифровой подписи
Параметрами схемы цифровой подписи являются:
- простое число р — модуль эллиптической кривой;
- эллиптическая кривая Е, задаваемая коэффициентами a, be Ер;
- целое число т — порядок группы точек эллиптической кривой Е;
- простое число q— порядок циклической подгруппы группы точек эллиптической кривой Е, для которого выполнены следующие условия:
5
(т =nq,n е Z,n>'\ (8)
|2254 <q< 2256или2508 < q < 2512’
- точка Р ф О эллиптической кривой Е, с координатами {хр, ур), удовлетворяющая равенству qP= О;
- хэш-функция V* -» V{, отображающая сообщения, представленные в виде двоичных векторов произвольной конечной длины, в двоичные векторы длины / бит. Хэш-функция определена в ГОСТ Р 34.11-2012. Если 2254 < q < 2256, то / = 256. Если 2508 < q< 2512, то /= 512.
Каждый пользователь схемы цифровой подписи должен обладать личными ключами:
- ключом подписи — целым числом d, удовлетворяющим неравенству 0 < d < q\
- ключом проверки подписи — точкой эллиптической кривой Q с координатами (xq, yq), удовлетворяющей равенству dP = Q.
К приведенным выше параметрам схемы цифровой подписи предъявляют следующие требования:
- должно быть выполнено условие р{ ф 1 (mod q) для всех целых f = 1, 2, ... В, где 6 = 31, если 2254 < q < 2256, и В = 131, если 2508< q < 2512;
- должно быть выполнено неравенство шф р;
- инвариант кривой должен удовлетворять условиям: J(E) ф 0 и J(E) ф 1728.
5.3 Двоичные векторы
Для определения процессов формирования и проверки цифровой подписи необходимо установить соответствие между целыми числами и двоичными векторами длины / бит.
(9)
Рассмотрим следующий двоичный вектор длиной / бит, в котором младшие биты расположены справа, а старшие — слева:
h (а^_.1, ---, ocq), /7 ь
где av / = 0,.., / - 1 равно либо 1, либо 0.
Число а е Z соответствует двоичному вектору Л, если выполнено равенство
(10)
/-1
а=Za/2'-
/=о
Для двух двоичных векторов
(11)
= (a/-i.....ао)>
^2= (Р/-1.....Ро).
соответствующих целым числам аир, операция конкатенации (объединения) определяется следующим образом:
hill ^2- (a/-1.....ao> Р/-1> ■■■>Ро)- (”12)
Объединение представляет собой двоичный вектор длиной 21 бит, составленный из компонент векторов /?1 и h2.
Формулы (11) и (12) определяют способ разбиения двоичного вектора hf\\h2 длиной 21 бит на два двоичных вектора длиной / бит, конкатенацией которых он является.
6 Основные процессы
В данном разделе определены процессы формирования и проверки цифровой подписи под сообщением пользователя.
Для реализации данных процессов необходимо, чтобы всем пользователям были известны параметры схемы цифровой подписи, соответствующие требованиям 5.2.
Кроме того, каждый пользователь должен иметь ключ подписи d и ключ проверки подписи Q(xq, yq), которые также должны соответствовать требованиям 5.2.
1
Оригиналы международных стандартов ИСО/МЭК находятся в ФГУП «Стандартинформ» Федерального агентства по техническому регулированию и метрологии.