ГОСТ 34100.3.1-2017
Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения. Дополнение 1. Трансформирование распределений с использованием метода Монте-Карло
Купить ГОСТ 34100.3.1-2017 — бумажный документ с голограммой и синими печатями. подробнее
Распространяем нормативную документацию с 1999 года. Пробиваем чеки, платим налоги, принимаем к оплате все законные формы платежей без дополнительных процентов. Наши клиенты защищены Законом. ООО "ЦНТИ Нормоконтроль"
Наши цены ниже, чем в других местах, потому что мы работаем напрямую с поставщиками документов.
Способы доставки
- Срочная курьерская доставка (1-3 дня)
- Курьерская доставка (7 дней)
- Самовывоз из московского офиса
- Почта РФ
В стандарте установлен численный метод, согласующийся с основными принципами GUM [ISO/IEC Guide 98-3:2008(G.1.5)] и предназначенный для получения оценки неопределенности измерения. Этот метод может быть применен к любым моделям, имеющим единственную выходную величину, в которых входные величины характеризуются любыми заданными функциями распределения вероятностей [ISO/IEC Guide 98-3:2008(G.1.4, G.5.3)].
Идентичен ISO/IEC Guide 98-3/Suppl 1:2008
Переиздание. Июль 2018
Оглавление
1 Область применения
2 Нормативные ссылки
3 Термины и определения
4 Соглашения и условные обозначения
5 Общие принципы
6 Плотности распределения вероятностей входных величин
7 Применение метода Монте-Карло
8 Проверка результатов
9 Примеры
Приложение А (справочное) Историческая справка
Приложение В (справочное) Коэффициенты чувствительности и бюджет неопределенности
Приложение С (справочное) Формирование выборок из распределений вероятностей
Приложение D (справочное) Непрерывная аппроксимация функции распределения выходной величины
Приложение Е (справочное) Интервал охвата для свертки четырех прямоугольных распределений
Приложение F (справочное) Задача определения коэффициента рассогласования
Приложение G (справочное) Основные обозначения
Приложение ДА (справочное) Сведения о соответствии ссылочных международных документов межгосударственным стандартам
Приложение ДБ (справочное) Дополнительные замечания к межгосударственным стандартам, вводящим международные руководства в области неопределенности измерения
Библиография
| Дата введения | 01.09.2018 |
|---|---|
| Добавлен в базу | 01.01.2018 |
| Актуализация | 01.01.2021 |
Этот ГОСТ находится в:
- Раздел Экология
Организации:
| 14.07.2017 | Утвержден | Межгосударственный Совет по стандартизации, метрологии и сертификации | 101-П |
|---|---|---|---|
| 12.09.2017 | Утвержден | Федеральное агентство по техническому регулированию и метрологии | 1066-ст |
| Разработан | МТК 125 Статистические методы в управлении качеством продукции | ||
| Издан | Стандартинформ | 2017 г. | |
| Издан | Стандартинформ | 2018 г. |
Uncertainty of measurement. Part 3. Guide to the expression of uncertainty in measurement. Supplement 1. Propagation of distributions using a Monte Carlo method
Чтобы бесплатно скачать этот документ в формате PDF, поддержите наш сайт и нажмите кнопку:

стр. 1

стр. 2

стр. 3

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14
стр. 15

стр. 16

стр. 17

стр. 18

стр. 19
стр. 20

стр. 21

стр. 22

стр. 23

стр. 24
стр. 25

стр. 26

стр. 27

стр. 28

стр. 29

стр. 30
МЕЖГОСУДАРСТВЕННЫЙ СОВЕТ ПО СТАНДАРТИЗАЦИИ, МЕТРОЛОГИИ И СЕРТИФИКАЦИИ
(МГС)
INTERSTATE COUNCIL FOR STANDARDIZATION. METROLOGY AND CERTIFICATION
(ISC)
МЕЖГОСУДАРСТВЕННЫЙ
СТАНДАРТ
ГОСТ34100.3.1—2017/
ISO/IEC Guide 98-3/Suppl 1:2008НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЯ
НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЯ
Часть 3
Руководство по выражению неопределенности измерения
Дополнение 1
Трансформирование распределений с использованием метода Монте-Карло
(ISO/IEC Guide 98-3/Suppl 1:2008, IDT)
Издание официальное
Москва
Стандартинформ
2017
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-2015 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-2015 «Межгосударственная система стандартизации. Стандарты межгосударственные. правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия. обновления и отмены»
Сведения о стандарте
1 ПОДГОТОВЛЕН Межгосударственным техническим комитетом по стандартизации МТК 125 «Статистические методы в управлении качеством продукции» на основе собственного перевода на русский язык англоязычной версии международного документа, указанного в пункте 5
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 14 июля 2017 г. № 101-П)
|
За принятие проголосовали: | |||||||||||||||
|
4 Приказом Федерального агентства по техническому регулированию и метрологии от 12 сентября 2017 г. № 1066-ст межгосударственный стандарт ГОСТ 34100.3.1-2017/ISO/IEC Guide 98-3/ Suppl 1 2008 введен в действие в качестве национального стандарта Российской Федерации с 1 сентября 2018 г.
5 Настоящий стандарт идентичен международному документу ISO/IEC Guide 98-3/Suppl 1 2008 «Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения. Дополнение 1. Трансформирование распределений с использованием метода Монте-Карло» («Uncertainly of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM 1995) — Supplement 1: Propagation of distributions using a Monte Carlo method». IDT).
Международный документ разработан Рабочей группой W3 1 Объединенного комитета по руководствам в метрологии JCGM.
Официальные экземпляры международного стандарта, на основе которого подготовлен настоящий межгосударственный стандарт, и международных стандартов, на которые даны ссылки, имеются в Федеральном агентстве по техническому регулированию и метрологии.
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных докуметов соответствующие им межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДА
6 ВВЕДЕН ВПЕРВЫЕ
3.18 способ оценивания неопределенности по GUM (GUM uncertainty framework): Применение закона трансформирования неопределенностей и описание выходной величины с помощью нормального распределения или масштабированного смещенного /-распределения, по которым может быть рассчитан соответствующий интервал охвата.
3.19 метод Монте-Карло (Monte-Carlo method): Метод трансформирования распределений на основе моделирования случайных выборок из этих распределений.
3.20 предел погрешности вычисления (numerical tolerance): Половина длины наименьшего интервала. содержащего все числа, отражающие результат вычислений, которые могут быть корректно представлены заданным числом значащих цифр.
При мор — При использовании в представлении результата вычисления двух значащих цифр записи 1,8 соответствуют все числа более 1,75 и менее 1,85. Тогда предел погрешности вычисления будет равен (1,85 - 1,75)12 « 0,05.
Примечание — Расчет предела погрешности вычисления — см. 7 9 2
4 Соглашения и условные обозначения
В настоящем стандарте использованы следующие соглашения и условные обозначения.
4.1 Математическая модель измерения [ISO/1EC Guide 98-3:2008 (4.1)) одномерной (скалярной) величины может быть представлена в виде функции t
Y- ЦХ), (1)
где У— выходная скалярная величина, а X— вектор N входных величин (X,.....Х^)т. Кахщая величина
X) рассматривается в качестве случайной переменной, принимающей значения с математическим ожиданием xt. У— случайная переменная, принимающая значения п. с математическим ожиданием у.
Примечание 1 — В настоящем стандарте один и тот же символ использован для физической величины и случайной переменной, которая эту величину представляет [см ISO/IEC Guide 98-3 2008 (4 1 1. примечание 1)].
Примечание 2 — Хотя многие модели измерений могут быть представлены формулой (1), более общим представлением является
/>(У.Х) = 0,
где X и У связаны между собой неявной функцией h В любом случае для применения метода Монте-Карло достаточно. чтобы каждому допустимому X было поставлено в соответствие значение У
4.2 Настоящий стандарт отступает от обозначений, часто используемых для обозначения плотностей распределения вероятностей и функций распределения (24). В GUM одно и то же обозначение f использовано как для функции измерения, так и для плотности распределения вероятностей, чем создается некоторая путаница. Поскольку в настоящем стандарте моделям уделено особое внимание, для плотности распределения вероятностей и функции распределения вместо обозначений (и F использованы соответственно ди 6. Используемые в обозначениях индексы соответствуют случайной переменной, о которой идет речь. Обозначение Г оставлено для описания функции измерения.
Примечание — Определения, приведенные в разделе 3, даны в соответствии с изложенным соглашением об обозначениях
4.3 В настоящем стандарте плотности распределения вероятностей могут быть определены для скалярной X или векторной х случайных переменных. Для скалярной случайной переменной X плотность распределения вероятностей обозначена g^q), где q — возможное значение X. Случайной переменной X соответствуют математическое ожидание Е(Х) и дисперсия ЦХ) (см. 3.6, 3.7).
4.4 Плотность распределения вероятностей векторной случайной переменной X обозначают
дх<£). где £ = (q,.....q^)T — вектор возможных значений X Вектор X рассматривают как вектор случай
ных переменных, которому соответствуют вектор математических ожиданий £(Х) и ковариационная матрица ЦХ)
4.5 Плотность распределения вероятностей нескольких случайных переменных часто называют совместной, даже если все входные величины являются независимыми.
4.6 Если элементы X, вектора X независимы, плотность распределения вероятностей X, обозначают дх(&.
4.7 Плотность распределения вероятностей и функцию распределения для У обозначают ду(г\) и Gy(n) соответственно.
5
4.8 В настоящем стандарте случайную переменную обозначают прописной буквой, а ее математическое ожидание или оценку — соответствующей строчной буквой. Например, оценку величины У (оценку ее математического ожидания) обозначают буквой у. Такое обозначение часто неудобно в случае физических величин, для которых традиционно используют иные символы, например Т для температуры и t для времени. Поэтому в некоторых примерах (раздел 9) использованы другие обозначения. В этом случае случайная переменная обозначена своим общепринятым символом, а ее оценка (оценка ее математического ожидания) — тем же символом с «крышкой». Например, отклонение калибруемой концевой меры длины от номинального значения при 20 °С (см. 9.5) обозначено 6L. а его оценка —SL.
Примечание — Символ с «крышкой» в литературе по математической статистике используют для обозначения оценки
4.9 В настоящем стандарте термин «закон трансформирования неопределенностей» используют в смысле аппроксимации функции измерения рядом Тейлора первого порядка. Этот термин также может быть применен при использовании разложения в ряд более высокого порядка.
4.10 Подстрочный индекс «с» для суммарной стандартной неопределенности [ISO/IEC Guide 98-3:2008 (5.1.1)] в настоящем стандарте рассматривается как излишний. Стандартная неопределенность оценки у выходной величины У может быть записана как и(у). хотя использование обозначения ис(у) остается допустимым, если это помогает заострить внимание на том. что имеется в виду суммарная стандартная неопределенность. Определение «суммарная» в данном контексте также является излишним и может быть опущено, поскольку присутствие символа «у» в и(у) уже указывает на оценку, с которой ассоциирована данная стандартная неопределенность. Еще более неуместным становится использование нижнего индекса «с» и определения «суммарная», когда результаты одного или нескольких измерений и соответствующие оценки неопределенности являются исходными данными для получения оценки неопределенности последующей величины.
4.11 В настоящем стандарте использованы термины «интервал охвата» и «вероятность охвата». В GUM в качестве синонима «вероятности охвата» использован термин «уровень доверия» с предупреждением. что это не то же самое, что «доверительная вероятность» (ISO/IEC Guide 98-3:2008 (6.2.2)]. поскольку последний термин имеет специальное определение в математической статистике. Так как в некоторых языках перевод с английского терминов «уровень доверия» и «доверительная вероятность» совпадает, в настоящем стандарте термин «уровень доверия» не используется.
4.12 Для обозначения десятичной дроби используется запятая1*.
4.13 Если не определено иначе, то числа представляют с заданным количеством значащих цифр.
Пример — Числа 0.060, 0.60, 6,0 и 60 представлены с точностью до двух значащих цифр. В этом случае запись с точностью только до одной значащей цифры: 0,06, 0,6 и 6-101 — будет некорректной.
4.14 Некоторые символы, использованные в настоящем стандарте, имеют более одного значения (см. приложение G). Однако их смысл понятен из контекста.
4.15 В настоящем стандарте использованы следующие сокращения:
CGPM — Генеральная конференция по мерам и весам;
IEEE — Институт инженеров электротехники и электроники;
JCGM — Объединенный комитет по руководствам в метрологии;
GUM — Руководство по выражению неопределенности измерения;
VIM — Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины.
5 Общие принципы
5.1 Основные этапы оценки неопределенности
5.1.1 Основные этапы оценки неопределенности включают в себя формулировку измерительной задачи, трансформирование распределений и получение окончательного результата:
а) формулировка измерительной задачи включает в себя:
1) задание выходной величины У (измеряемой величины);
2) выявление входных величин X = (X,.....от которых зависит выходная величина У;
3) составление модели измерения, определяющей взаимосвязь У с входными величинами X:
'* В оригинале на английском языке в данном подразделе указывается на использование в качестве десятичного знака точки вместо запятой 6
4) приписывание распределений вероятностей (нормального, прямоугольного и т. д.) входным величинам X, (или совместного распределения вероятностей входным величинам, не являющимся независимыми) на основе имеющейся информации.
b) трансформирование распределений предусматривает определение плотности распределения вероятностей выходной величины У на основе плотностей распределения вероятностей входных величин X, и используемой модели измерения,
c) получение окончательного результата предполагает использование плотности распределения вероятностей выходной величины У для определения:
1) оценки математического ожидания величины У в виде оценки у.
2) оценки стандартного отклонения величины У в виде стандартной неопределенности и(у). ассоциированной с у (ISO/IEC Guide 98-3:2008 (Е.3.2)];
охвата).
3) интервала охвата для величины У. соответствующего заданной вероятности (вероятности
Примечание 1 — В некоторых случаях оценка выходной величины в виде математического ожидания может оказаться неприемлемой [см ISO/IEC Guide 98-3 2008 (4 1 4)).
Примечание 2 — Некоторые величины, например подчиняющиеся распределению Коши, не имеют математического ожидания и стандартного отклонения Однако интервал охвата для выходной величины всегда может быть построен
5.1.2 При оценке неопределенности no GUM функции распределения входных величин в явном виде не используют. Однако в соответствии с ISO/IEC Guide 98-3:2008 (3.3.5) «...стандартную неопределенность типа А рассчитывают по плотности распределения вероятностей..., полученной из распределения частот ... а стандартную неопределенность типа В — по предполагаемой плотности распределения вероятностей, отражающей степень уверенности в появлении того или иного события... Оба подхода используют общепринятые интерпретации понятия вероятности».
Примечание — Трактовка распределения вероятностей при определении оценки неопределенности типа В характерна для байесовского анализа [21. 27] В настоящее время продолжаются исследования [22] границ применимости формулы Уэлча-Саттертуэйта для расчета числа степеней свободы, приписываемых стандартной неопределенности.
5.1.3 Формулировку измерительной задачи осуществляет метролог с возможным участием специалиста в той области знаний, в которой проводят измерение. В настоящем стандарте приведены рекомендации по выбору плотности распределения вероятностей [стадия 4) этапа а) в соответствии с 5.1.1] для некоторых общих случаев (см. 6.4). Этапы трансформирования распределений и получения окончательных результатов [б) и в) в соответствии с 5.1.1], для которых приведены подробные указания, не требуют дополнительной метрологической информации и могут быть выполнены с любой допустимой точностью для поставленной задачи.
Примечание — Как только этап постановки задачи а) в соответствии с 5 1 1 выполнен, тем самым плотность распределения вероятностей для выходной величины формально полностью определена Однако вычисление математического ожидания, стандартного отклонения и интервала охвата может потребовать применения численных методов, обладающих некоторой степенью приближения
5.2 Трансформирование распределений
В настоящем стандарте рассматривается общий эффективный способ определения (численным методом) функции распределения случайной переменной У:
|
Примечание — Формально плотность распределения вероятностей случайной переменной У можно представить в следующем виде [9] |
Этот способ основан на применении метода Монте-Карло для трансформирования распределений входных величин (см. 5.9).
7
где б(г) - /($)) — дельта функция Дирака, и применять численные методы вычисления N-кратного интеграла (поскольку в общем случае он не может быть взят аналитически) Однако такой способ численного вычисления плотности распределения вероятностей У неэффективен
5.3 Получение окончательного результата
5.3.1 Оценка у входной величины У представляет собой оценку математического ожидания Е(У). Стандартная неопределенность и(у) оценки у представляет собой оценку стандартного отклонения У, т. е. положительный квадратный корень из дисперсии V(Y).
5.3.2 Интервал охвата для У может быть определен на основе Gy<n). Если задать требуемую вероятность охвата р и взять любое число о из интервала от нуля до (1 - р). то границами 100р %-ного интервала охвата для У будут значения Gy1 (о) и Gy'(p + а), т. е. квантили распределения Gy<n) уровней « и р + а соответственно.
5.3.3 Выбора = (1 -р)/2 позволяет определить вероятностно симметричный 100р%-ный интервал охвата, границами которого являются квантили уровней (1 -р)/2 и (1 + р)/2.
Примечание — Если плотность распределения вероятностей для У симметрична относительно математического ожидания у, то полученный интервал будет совпадать с интервалом y±Up где расширенная неопределенность Up [ISO/IEC Guide 98-3 2008 (2 3 5)) равна произведению стандартной неопределенности и(у) на коэффициент охвата, соответствующий данной плотности распределения вероятностей В общем случае плотность распределения вероятностей выходной величины не может быть выражена в аналитическом виде
5.3.4 Если плотность распределения вероятностей асимметрична, то более подходящим мо
жет быть выбор а, отличающейся от (1 - р)Г2, например позволяющий получить наименьший 100р%-ный интервал охвата. Если плотность распределения вероятностей унимодальна, то оно обладает таким свойством, что наименьший интервал охвата будет включать в себя моду этого распределения. Данному интервалу будет соответствовать значение а, удовлетворяющее соотношению g^Gy1 (а)] = = + а)). В случае распределения общего вида значение а. соответствующее наименьшему
100р %-ному интервалу охвата, должно быть таким, чтобы разность Gy’(p + а) - Gy1 (а) была минимальна.
5.3.5 Для симметричной плотности распределения вероятностей, например для нормального или масштабированного смещенного /-распределения, используемых при оценивании неопределенности по GUM, вероятностно симметричный и наименьший 100р %-ный интервалы охвата совпадают между собой. Поэтому в способе оценивания неопределенности по GUM эти интервалы не различают.
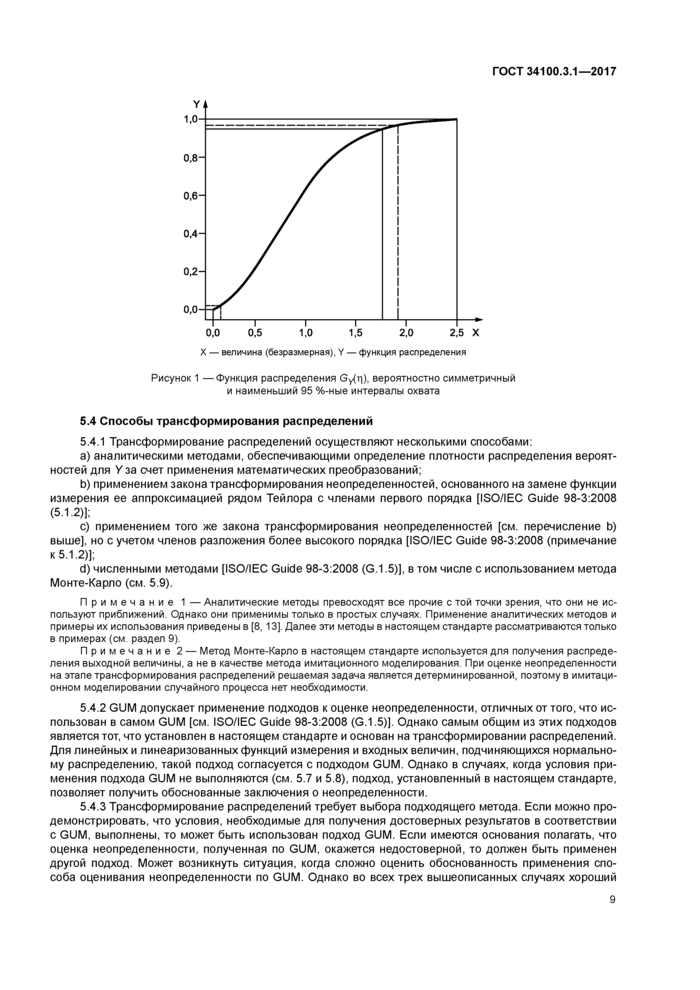
5.3.6 На рисунке 1 показана функция распределения Gy(n). соответствующая асимметричной плотности распределения вероятностей. Пунктирными вертикальными линиями показаны границы вероятностно симметричного 95 %-ного интервала охвата, а пунктирными горизонтальными линиями — соответствующие значения вероятности -0,025 и 0,975. Сплошными линиями показаны границы наименьшего 95 %-ного интервала охвата и соответствующие значения вероятности, которые в данном случае равны 0.006 и 0.956. Длина этих двух интервалов охвата для данного примера составляет соответственно 1,76 и 1,69.
8
|
X — величина (безразмерная). Y — функция распределения Рисунок 1 — Функция распределения Gy(n). вероятностно симметричный и наименьший 95 %-ные интервалы охвата |
5.4 Способы трансформирования распределений
5.4.1 Трансформирование распределений осуществляют несколькими способами:
a) аналитическими методами, обеспечивающими определение плотности распределения вероятностей для У за счет применения математических преобразований:
b) применением закона трансформирования неопределенностей, основанного на замене функции измерения ее аппроксимацией рядом Тейлора с членами первого порядка [ISO/IEC Guide 98-3:2008 (5.1-2)1;
c) применением того же закона трансформирования неопределенностей (см. перечисление Ь) выше], но с учетом членов разложения более высокого порядка [ISO/IEC Guide 98-3:2008 (примечание к 5.1.2)];
d) численными методами (ISO/IEC Guide 98-3:2008 (G.1.5)]. в том числе с использованием метода Монте-Карло (см. 5.9).
Примечание 1— Аналитические методы превосходят все прочие с той точки зрения, что они не используют приближений Однако они применимы только в простых случаях Применение аналитических методов и примеры их использования приведены в (8,13] Далее эти методы в настоящем стандарте рассматриваются только в примерах (см раздел 9)
Примечание 2 — Метод Монте-Карло в настоящем стандарте используется для получения распределения выходной величины, а не в качестве метода имитационного моделирования При оценке неопределенности на этапе трансформирования распределений решаемая задача является детерминированной, поэтому в имитационном моделировании случайного процесса нет необходимости
5.4 2 GUM допускает применение подходов к оценке неопределенности, отличных от того, что использован в самом GUM [см. ISO/IEC Guide 98-3:2008 (G.1.5)]. Однако самым общим из этих подходов является тот. что установлен в настоящем стандарте и основан на трансформировании распределений. Для линейных и линеаризованных функций измерения и входных величин, подчиняющихся нормальному распределению, такой подход согласуется с подходом GUM. Однако в случаях, когда условия применения подхода GUM не выполняются (см. 5.7 и 5.8), подход, установленный в настоящем стандарте, позволяет получить обоснованные заключения о неопределенности.
5.4.3 Трансформирование распределений требует выбора подходящего метода. Если можно продемонстрировать, что условия, необходимые для получения достоверных результатов в соответствии с GUM. выполнены, то может быть использован подход GUM. Если имеются основания полагать, что оценка неопределенности, полученная no GUM. окажется недостоверной, то должен быть применен другой подход. Может возникнуть ситуация, когда сложно оценить обоснованность применения способа оценивания неопределенности по GUM. Однако во всех трех вышеописанных случаях хороший
9
результат может быть получен с использованием метода Монте-Карло. В первом случае метод Монте-Карло может быть проще в применении, например, вследствие трудностей вычисления коэффициентов чувствительности [ISO/IEC Guide 98-3:2008 (5.1.3)]. Во втором случае метод Монте-Карло позволит получить достоверный результат, так как его применение не требует использования дополнительных предположений. В третьем случае метод Монте-Карло может быть применен как собственно для получения оценки неопределенности, так и для оценки качества результатов, полученных способом расчета неопределенности no GUM.
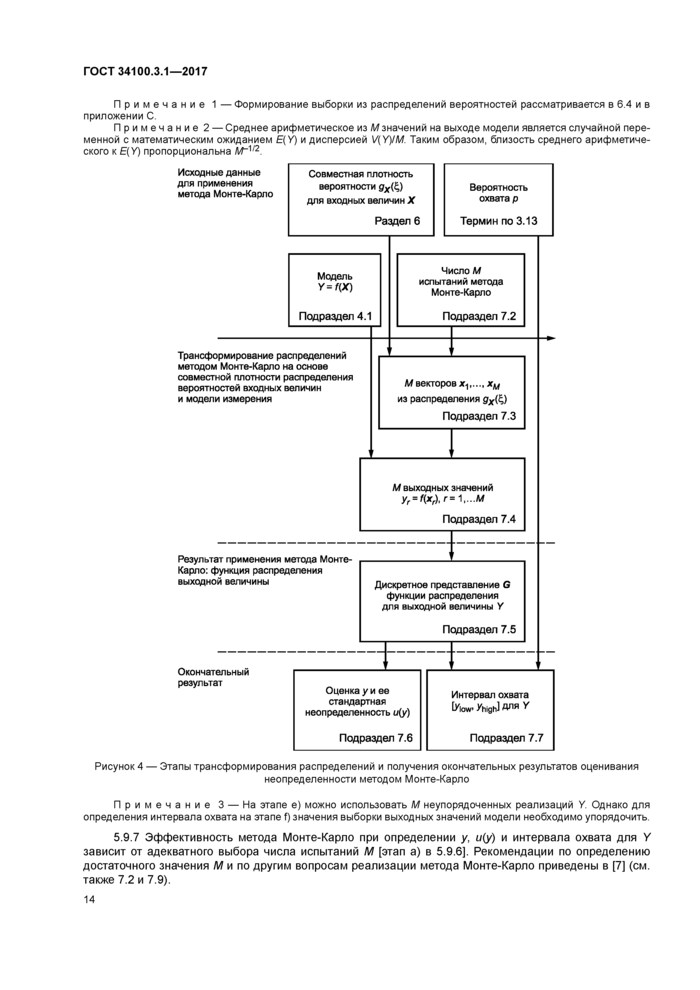
5.4 4 Трансформирование моделью измерений плотностей распределения вероятностей дх(с^).
i-^.....N входных величин X, для получения плотности распределения вероятностей (?у(п) выходной
|
Рисунок 2 — Трансформирование распределений трех (Л/ = 3) независимых входных величин |
величины У. показано на рисунке 2 для трех независимых X, (N = 3). Рисунок 2 можно сравнить с рисунком 3. иллюстрирующим закон трансформирования неопределенностей. На рисунке 2 функции дх(с*). /=1.2.3 представляют собой плотности распределения вероятностей случайных переменных, подчиняющихся соответственно нормальному, треугольному и нормальному законам. Соответственно функция 9у(п) показана асимметричной, что обычно имеет место в случае нелинейных моделей или асимметрии функций дх(с£.
W
9* ifti)
А
9*г($2>
А
9»3(£з)
5.4.5 На практике только в самых простых случаях преобразование распределений может быть выполнено без приближений. При оценке неопределенности по GUM применяется один метод приближения. в методе Монте-Карло — другой. Для небольшой, но важной подгруппы задач оценки неопределенности в соответствии с GUM не требуется применения приближений (решение является точным). Метод Монте-Карло не позволяет получить точные результаты, но для широкого класса задач он будет более обоснованным, чем подход GUM
5.5 Представление результатов
5.5.1 После выполнения трансформирования распределений должна быть отражена, как правило, следующая информация:
a) оценка у выходной величины У;
b) стандартная неопределенность и(у) оценки у;
c) заданная 100р %-ная (например. 95 %-ная) вероятность охвата:
d) границы выбранного 100р %-ного (например. 95 %-ного) интервала охвата для У;
e) другая значимая информация, такая как тип интервала охвата (вероятностно симметричный или наименьший).
5.5.2 Значения у. и(у) и границ 100р %-ного интервала охвата для У должны быть указаны с таким количеством значащих цифр, чтобы низший разряд записи значения этих величин совпадал с низшим разрядом, используемым для записи и(у) [ISO/IEC Guide 98-3:2008 (7.2.6)]. Обычно для представления и(у) достаточно одной или двух значащих цифр.
Примечание 1 — Представляемое численное значение обычно получают путем округления числа, содержащего большее количество значащих цифр
Примечание 2 — Фактором, влияющим на выбор представления результатов одной или двумя значащими цифрами, является значащая цифра высшего разряда в значении и(у) Если это 1 или 2. то погрешность округления и(у) будет сопоставима с самим значением величины Если же первая значащая цифра равна 9. то относительная погрешность округления будет меньше
10
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе «Национальные стандарты» (по состоянию на 1 января текущего года), а текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены наспюящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указапюле «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
© Стандартинформ. 2017
В Российской Федерации настоящий стандарт не может быть полностью или частично воспроизведен. тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
Содержание
1 Область применения....................................................................................................................................1
2 Нормативные ссылки....................................................................................................................................2
3 Термины и определения...............................................................................................................................2
4 Соглашения и условные обозначения........................................................................................................5
5 Общие принципы..........................................................................................................................................6
6 Плотности распределения вероятностей входных величин...................................................................16
7 Применение метода Монте-Карло.............................................................................................................26
8 Проверка результатов................................................................................................................................32
9 Примеры......................................................................................................................................................33
Приложение А (справочное) Историческая справка...................................................................................55
Приложение В (справочное) Коэффициенты чувствительности и бюджет неопределенности..............56
Приложение С (справочное) Формирование выборок из распределений вероятностей........................57
Приложение D (справочное) Непрерывная аппроксимация функции распределения выходной
величины..............................................................................................................................62
Приложение Е (справочное) Интервал охвата для свертки четырех прямоугольных
распределений....................................................................................................................64
Приложение F (справочное) Задача определения коэффициента рассогласования..............................65
Приложение G (справочное) Основные обозначения................................................................................68
Приложение ДА (справочное) Сведения о соответствии ссылочных межаународных
документов межгосударственным стандартам...............................................................71
Приложение ДБ (справочное) Дополнительные замечания к межгосударственным стандартам, вводящим международные руководства в области
неопределенности измерения.........................................................................................72
Библиография................................................................................................................................................75
IV
Введение
0.1 Общие сведения
В настоящем стандарте рассматривается трансформирование распределений для заданной математической модели измерений (ISO/IEC Guide 98-3:2008 (3.1.6)) с целью получения оценки неопределенности измерений и реализация этой процедуры методом Монте-Карло. Метод применим к моделям с произвольным числом входных величин и единственной выходной величиной.
Метод Монте-Карло является практической альтернативой способу оценки неопределенности по GUM (ISO/IEC Guide 98-3:2008 (3 4 8)). Метод имеет особое значение, когда:
a) линеаризация модели не обеспечивает ее адекватного представления;
b) распределение выходной величины, например, вследствие своей выраженной асимметрии не может быть описано нормальным распределением (распределением Гаусса) или масштабированным смещенным /-распределением.
В случае а) оценки выходной величины и соответствующей стандартной неопределенности, полученные в соответствии с GUM. могут оказаться недостоверными. В случае Ь) при оценке неопределенности могут быть получены недостоверные интервалы охвата (обобщение понятия расширенной неопределенности, используемого в GUM).
GUM [ISO/IEC Guide 98-3:2008 (3.4.8)) «...устанавливает общую методологию оценивания неопределенности...». основанную на использовании закона трансформирования неопределенностей (ISO/IEC Guide 98-3:2008 (раздел 5)). когда выходная величина подчиняется нормальному распределению или масштабированному смещенному /-распределению [ISO/IEC Guide 98-3:2008 (G.6.2, G.6 4)). При этом закон трансформирования неопределенностей позволяет учесть неопределенности входных величин и вычислить стандартную неопределенность оценки выходной величины на основе:
1) наилучших оценок входных величин;
2) стандартных неопределенностей оценок входных величин;
3) числа степеней свободы для стандартных неопределенностей оценок входных величин;
4) всех ненулевых ковариаций пар этих оценок.
Кроме того, полученная плотность распределения вероятностей выходной величины позволяет определить для выходной величины интервал охвата с заданной вероятностью.
Наилучшие оценки входных величин, их стандартные неопределенности, ковариации и числа степеней свободы представляют собой ту информацию, которая необходима для применения метода расчета неопределенности по GUM. Метод, устанавливаемый настоящим стандартом, основан на использовании плотностей распределения вероятностей входных величин для последующего расчета плотности распределения вероятностей выходной величины.
В то время как для применения способа оценивания неопределенности по GUM существуют некоторые ограничения, трансформирование распределений всегда позволяет получить плотность распределения вероятностей выходной величины на основе распределений входных величин. Плотность распределения вероятностей выходной величины представляет собой выражение знания об этой величине, полученного на основе знаний о входных величинах в виде сопоставленных им распределений. После получения плотности распределения вероятностей выходной величины могут быть определены математическое ожидание, используемое в качестве оценки выходной величины, и стандартное отклонение, используемое в качестве стандартной неопределенности этой оценки. Кроме того, плотность распределения вероятностей может быть использована для получения интервала охвата для выходной величины, соответствующего заданной вероятности.
Использование плотностей распределения вероятностей в соответствии с настоящим стандартом в основном согласуется с принципами GUM. Плотность распределения вероятностей величины отражает состояние знаний об этой величине, т. е. она численно определяет степень доверия тем значениям, которые могут быть приписаны упомянутой величине на основе доступной информации. Информация обычно состоит из необработанных статистических данных, результатов измерения, научных выводов, профессиональных суждений.
Для построения плотности распределения вероятностей случайной переменной на основе наблюдений может быть применена теорема Байеса (27. 33). Информация о систематических эффектах может быть преобразована в соответствующую плотность распределения вероятностей на основе принципа максимума энтропии [51. 56).
V
Трансформирование распределений имеет более широкую область применения, чем способ оценивания неопределенности no GUM Метод трансформирования распределений использует более обширную информацию, чем та. что содержится в наилучших оценках и соответствующих стандартных неопределенностях (а также в числах степеней свободы и ковариациях).
Исторический обзор приведен в приложении А.
Примечание 1 — В GUM рассматривается случай, когда линеаризация модели измерения неприменима [ISO/IEC Guide 98-3 2008 (примечание к 5.1.2)). Однако это рассмотрение ограничено использованием только основных нелинейных членов в ряде Тейлора для функции измерения, а также предположением о нормальности распределения входных величин
Примечание 2 — Строго говоря, в GUM ^-распределение описывает не выходную величину У. а величину (У-у)/о(у) [точнее, как указано в GUM. (у - У)/и(у)]. где у—оценка У. и(у) — стандартная неопределенность оценки у [ISO/IEC Guide 98-3 2008 (G 3 1)). Такое представление использовано и в настоящем стандарте
Примечание 3 — Плотность распределения вероятностей не следует понимать в смысле частотного описания вероятности
Примечание 4 — «Оценивание неопределенности нельзя рассматривать как типовую задачу, требующую применения стандартных математических процедур От пользователя требуется детальное знание природы измеряемой величины и процедуры измерения Поэтому качество оценки неопределенности, приписанной результату измерений, зависит в конечном счете от понимания, критического анализа и профессиональной добросовестности всех лиц, принимающих участие в ее получении» (17).
0.2 Основные сведения о JCGM
В 1997 г. семью международными организациями, подготовившими в 1993 г. «Руководство по выражению неопределенности измерения» (GUM) и «Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины» (VIM). был образован Объединенный комитет по руководствам в метрологии (JCGM), возглавляемый директором Международного Бюро Мер и Весов (МБМВ), который принял на себя ответственность за указанные документы от Технической консультативной группы по метропогии (ИСО/ТАГ 4).
Учредителями JCGM помимо МБМВ являются Международная электротехническая комиссия (МЭК), Международная федерация клинической химии и лабораторной медицины (МФКХ), Международное сотрудничество по аккредитации лабораторий (ИЛАК), Международная организация по стандартизации (ИСО). Международный союз теоретической и прикладной химии (ИЮПАК). Международный союз теоретической и прикладной физики (ИЮПАП) и Международная организация по законодательной метрологии (МОЗМ).
В рамках JCGM созданы две Рабочие группы (РГ). Задачей РГ 1 «Выражение неопределенности измерения» являются содействие использованию Руководства (GUM), подготовка дополнений к Руководству и иных документов, способствующих его широкому применению. Задачей РГ 2 «Рабочей группы по Международному словарю основных и общих терминов в метрологии (VIM)» являются пересмотр VIM и содействие его применению. Более подробную информацию о деятельности JCGM можно найти на сайте www.bipm.org.
Дополнения к GUM, подобные тому, что положено в основу настоящего стандарта, имеют целью распространить руководство на те аспекты, которые в этом руководстве 8 полной мере не отражены. При этом, однако, разрабатываемые дополнения соответствуют, насколько это возможно, общей методологии. изложенной в GUM.
VI
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЯ Часть 3
Руководство по выражению неопределенности измерения Дополнение 1
Трансформирование распределений с использованием метода Монте-Карло
Uncertainty of measurement Part 3 Guide to the expression of uncertainty in measurement Supplement 1. Propagation of distnbutions using a Monte-Carlo method
Дата введения — 2018—09—01
1 Область применения
В настоящем стандарте установлен численный метод, согласующийся с основными принципами GUM (ISO/IEC Guide 98-3:2008 (G.1.5)] и предназначенный для получения оценки неопределенности измерения. Этот метод может быть применен к любым моделям, имеющим единственную выходную величину. в которых входные величины характеризуются любыми заданными функциями распределения вероятностей [ISO/IEC Guide 98-3:2008 (G.1.4. G.5.3)).
Так же как GUM. настоящий стандарт посвящен вопросам определения выражения для неопределенности измерения хорошо определенной физической величины, характеризуемой единственным значением [ISO/IEC Guide 98-3:2008 (1.2)].
В настоящем стандарте установлены также методы, применимые в ситуациях, когда условия применения способа расчета неопределенности по GUM [ISO/IEC Guide 98-3:2008 (G.6.6)] не выполняются или информация об их выполнении отсутствует. Стандарт также может быть применен в ситуациях, когда возникают трудности при оценке неопределенности по GUM. например вследствие сложности модели. Методы изложены в виде, облегчающем их программирование для расчетов на компьютере.
Настоящий стандарт может быть использован для определения плотности распределения вероятностей выходной величины, что позволяет получить:
a) оценку выходной величины;
b) стандартную неопределенность, ассоциированную с этой оценкой;
c) интервал охвата для выходной величины, соответствующий заданной вероятности охвата.
При заданных (i) модели, описывающей взаимосвязь входных величин с выходной величиной.
и (й) плотностях распределения вероятностей входных величин существует единственная плотность распределения вероятностей выходной величины. Как правило, последняя не может быть определена аналитически. Настоящий стандарт позволяет определить величины, указанные в перечислениях а). Ь) и с) с приемлемой точностью, не используя приближений, которые нельзя оценить количественно.
Настоящий стандарт позволяет получить интервал охвата для заданной вероятности охвата, в том числе вероятностно симметричный и наименьший интервалы.
Настоящий стандарт применим к статистически независимым входным величинам с соответствующими функциями плотности распределения вероятностей, а также к статистически зависимым случайным переменным, описанным совместной плотностью распределения.
Как правило, настоящий стандарт применяют в случаях, когда:
- вклад разных составляющих неопределенности может быть существенно неодинаков [ISO/IEC Guide 98-3:2008 (G.2.2)];
-трудно или неудобно находить частные производные от функции измерения, как того требует закон трансформирования неопределенностей;
Издание официальное
- распределение выходной величины нельзя считать ни нормальным, ни масштабированным смещенным t-распределением [ISO/IEC Guide 98-3:2008 (G.6.5)J:
- оценка выходной величины и соответствующая стандартная неопределенность имеют приблизительно одинаковое значение (ISO/IEC Guide 98-3:2008 (G.2.1));
- модель является достаточно сложной (ISO/IEC Guide 98-3:2008 (G.1.5));
- плотности распределения вероятностей входных величин асимметричны [ISO/IEC Guide 98-3:2008 (G 5.3)).
Прежде чем применять метод, установленный настоящим стандартом, рекомендуется проверить, позволяют ли условия измерительной задачи использовать способ оценивания неопределенности по GUM Если условия позволяют, то основным методом расчета остается оценивание неопределенности способом, установленным в GUM.
Значение для неопределенности измерений, как правило, достаточно приводить с одной или двумя значащими цифрами. Методы, установленные настоящим стандартом, позволяют получить оценки с указанной точностью.
Применение стандарта иллюстрировано подробными примерами.
Настоящий стандарт служит дополнением к GUM и должен быть использован вместе с ним. Он не исключает использования других методов расчета неопределенности, не противоречащих GUM
Примечание 1 — Настоящий стандарт неприменим к моделям, описываемым многозначными функциями (например, в виде решения квадратного уравнения без указания, какой из корней должен быть выбран)
Примечание 2 — В настоящем стандарте не рассмотрен случай, когда априорно известна плотность распределения вероятностей выходной величины, однако установленный в нем метод может быть модифицирован и для этой ситуации (16).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие документы:
ISO/IEC Guide 98-3:2008. Uncertainty of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM: 1995) (Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения (GUM 1995))
ISO/IEC Guide 99:2007, International vocabulary of metrology — Basic and general concepts and associated terms (VIM) (Международный словарь no метрологии. Основные и общие понятия и связанные с ними термины (VIM))
3 Термины и определения
В настоящем стандарте применены термины no ISO/IEC Guide 98-3 и ISO/IEC Guide 99. некоторые из которых (при необходимости модифицированные) приведены в настоящем разделе.
Обозначения, использованные в настоящем стандарте, приведены в приложении G.
3.1 распределение (вероятностей) (probability distribution): Функция, устанавливающая вероятность того, что случайная переменная принимает заданное значение или принадлежит к заданному множеству значений.
Примечание — Сумма вероятностей принятия случайной переменной всех возможных значений равна 1
(Модифицировано по отношению к ISO 3534-1:1993, словарная статья 1.3, ISO/IEC Guide 98-3:2008. словарная статья С.2.3)
Примечание 1 — Распределение вероятностей называется одномерным, если оно описывает поведение единственной (скалярной) случайной переменной, и многомерным, если оно описывает поведение вектора случайных переменных Многомерное распределение вероятностей описывается также совместным распределением этих случайных переменных
Примечание 2 — Распределение вероятностей может быть представлено в виде функции распределения и плотности распределения вероятностей
3.2 функция распределения (вероятностей) (distribution function): Функция, устанавливающая для каждого значения q вероятность того, что случайная переменная X меньше или равна q:
Gx(q) = Pr(X < q).
[Модифицировано no отношению к ISO 3534-1:1993, словарная статья 1.4; ISO/IEC Guide 98-3:2008, словарная статья С.2.4)
2
3.3 плотность распределения (вероятностей) (probability density function): Первая производная, если она существует, функции распределения непрерывной случайной переменной
0х6> = dG^/dq.
Примечание — д*(с,№, называется «элементом вероятности»:
$♦<*;).
(Модифицировано по отношению к ISO 3534-1:1993. словарная статья 1.5; ISO/IEC Guide 98-3:2008. словарная статья С.2.5]
|
Примечание — р — математическое ожидание X, о — стандартное отклонение X |
3.4 нормальное распределение (вероятностей) (nonnal distribution): Распределение вероятностей непрерывной случайной переменной X такое, что соответствующая плотность распределения вероятностей для - « < £ < + оо имеет вид:
(Модифицировано по отношению к ISO 3534-1:1993. словарная статья 1.37; Руководство ISO/IEC Guide 98-3:2008. словарная статья С.2.14]
Примечание — Нормальное распределение называют также распределением Гаусса
кг
Г К v +1)/2( 7яуГ(у/2)
0х(^) =
3.5 /-распределение (/-distribution): Распределение вероятностей непрерывной случайной переменной X. плотность распределения вероятностей которой для - » < q < + <» имеет вид
где v — число степеней свободы (положительное целое число);
00
Г(г)= jV ’е 'dt — гамма-функция, z > 0.
о
3.6 математическое ожидание (expectation): Характеристика случайной переменной, которая для непрерывной случайной переменной X с плотностью распределения вероятностей д^^) имеет вид
Примечание 1 — Не всякая случайная переменная имеет математическое ожидание
Примечание 2 — Математическое ожидание случайной переменной Z = Я(Х) имеет вид
E(Z) = E[F(X)]= jF(5)0xKK-
3.7 дисперсия (variance): Характеристика случайной переменной, которая для непрерывной случайной переменной X с плотностью распределения вероятностей имеет вид
VW-
Примечание — Не всякая случайная переменная имеет дисперсию
3.8 стандартное отклонение (standard deviation): Положительный квадратный корень из дисперсии. (ЦХ))1*.
£(*')= J
3.9 момент порядка г (moment of order г): Математическое ожидание r-й степени случайной переменной
Примечание 1 — Центральным моментом порядка г является математическое ожидание случайной переменной Z = (X - E(X)f
Примечание 2 — Математическое ожидание £(Х) представляет собой момент первого порядка Дисперсия ЩХ) является центральным моментом второго порядка
3.10 ковариация (covariance): Характеристика двух случайных переменных, которая в случае непрерывных случайных переменных Х1 и Х2 с совместной плотностью распределения gx(£). где X-(X,, Х2)т $ =(q,. £2)т. имеет вид
Cov(X,.X2) =
Примечание — Не все пары случайных переменных имеют ковариацию
3.11 матрица неопределенности (uncertainty matrix): Матрица размерности /V * N. на главной диагонали которой расположены квадраты стандартных неопределенностей, соответствующих оценкам-компонентам векторной величины размерности N. а остальные элементы представляют собой ковариации для соответствующих оценок.
Примечание 1 — Матрица неопределенности Ux размерности N * N. соответствующая вектору оценок х векторной величины X, имеет вид:
и*
u(x,.xN)
u{xN.xN)
где uiXj, Xj) = u2(x,-) — дисперсия (квадрат стандартной неопределенности) оценки xt
u(xh yj) — ковариация xt и xf u(x,, xf) = 0. если элементы X\ и X; вектора X некореллированны Примечание 2 — Ковариации также можно трактовать как совместные неопределенности Примечание 3 — Матрицу неопределенности также называют матрицей ковариаций или дисперсионноковариационной матрицей
3.12 интервал охвата1* (coverage interval): Интервал, построенный на основе имеющейся информации и содержащий значение случайной переменной с заданной вероятностью.
Примечание 1 — Интервал охвата иногда называют байесовским интервалом
Примечание 2 — В общем случае для заданной вероятности существует более одного интервала охвата
Примечание 3 — Интервал охвата не следует называть доверительным интервалом, чтобы избежать путаницы с термином, имеющим строгую статистическую интерпретацию (ISO/IEC Guide 98-3 2008 (б 2 2)]
Примечание 4 — Данное определение отличается от определения, приведенного в ISO/IEC Guide 99 2007. поскольку в настоящем стандарте не использован термин «истинное значение* по причинам, изложенным в GUM (ISO/IEC Guide 98-3 2008 (Е 5))
3.13 вероятность охвата (coverage probability): Вероятность того, что значение случайной переменной находится в границах интервала охвата.
Примечание — Вероятность охвата иногда называют уровнем доверия (Руководство ISO/IEC Guide 98-3 2008 (6 2 2)]
3.14 длина интервала охвата (length of a coverage interval): Разность наибольшего и наименьшего значений интервала охвата.
3.15 вероятностно симметричный интервал охвата (probabilistically symmetric coverage interval): Интервал охвата, для которого вероятность того, что значение случайной переменной меньше наименьшего значения (нижней границы) интервала охвата, равна вероятности того, что значение случайной переменной больше наибольшего значения (верхней границы) интервала.
3.16 наименьший интервал охвата (shortest coverage interval): Интервал охвата, имеющий наименьшую длину среди всех возможных интервалов охвата для данной случайной переменной с одинаковой вероятностью охвата.
3.17 трансформирование распределений (propagation of distributions): Метод, используемый для определения распределения выходной величины на основе распределения входных величин, от которых выходная величина зависит функционально.
Примечание — Метод может быть аналитическим или численным, точным или приближенным
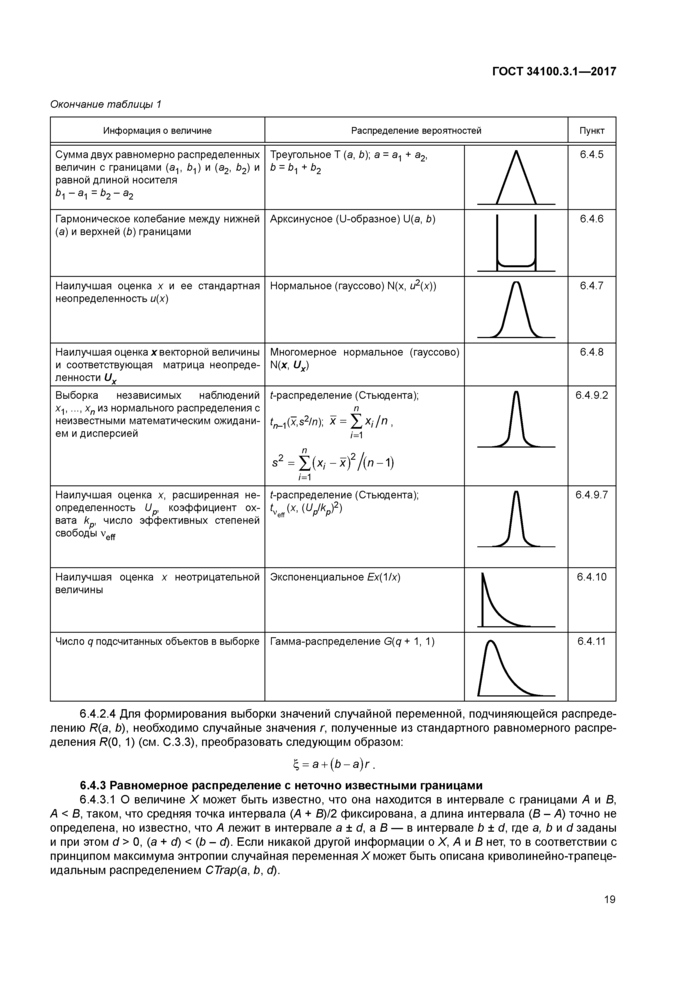
^ В отечественных нормативных документах интервал охвата иногда называют интервалом неопределенности